基于CFD-DEM 的固液分级过滤模拟
2022-10-25赵钟杰张建鹏唐艳玲黄子宾程振民
赵钟杰, 张建鹏, 唐艳玲, 肖 桐, 黄子宾, 程振民
(华东理工大学化学工程联合国家重点实验室,上海 200237)
颗粒层过滤作为一种低成本的分离方式被人们广泛关注,并应用于烟气除尘、水处理、油浆净化等领域[1-3]。研究者们总结了包括惯性碰撞、拦截和扩散等在内的基本颗粒层过滤机理,得出了过滤性能与流速、粒径、床层深度等因素有关的结论[4-6]。Zamani 等[7]归纳了颗粒层过滤的微观和宏观模型,这些模型的应用范围是非普适性的,均存在各自的缺点:如宏观经验模型无法揭示内部过滤机理;随机模型无法计算过滤效率;迹线模型无法计算过滤压降等。
由于上述模型应用的局限性,计算流体力学(Computational Fluid Dynamics,CFD) 和离散单元法(Discrete Element Method,DEM) 耦合模拟的方法被许多研究者所重视,并被应用于过滤研究。Qian 等[8]利用随机算法构建了三维纤维过滤器模型,并采用CFD-DEM 耦合方法研究不同气速和空隙率下的气溶胶过滤性能。Yue 等[9]基于CFD-DEM 的耦合模型对含尘气体的过滤进行了模拟,全面分析了颗粒的运动以及颗粒所受接触力对过滤性能的影响。肖桐等[10]采用CFD-DEM 耦合方法,构建三维随机堆积的颗粒床模型,研究不同时刻和表观过滤速率下颗粒沉积的变化,并考虑了颗粒沉积对于过滤效率和压降的影响。
颗粒层过滤器中杂质颗粒的沉积分布通常是不均匀的,当滤料粒径较小时,颗粒更容易沉积在过滤器前端[11],床层深处的滤料几乎没有被利用。滤料粒径越小,过滤效率越高,然而这也意味着过滤器容垢能力的降低。为了同时提高过滤效率和容垢量,分级过滤器的概念被提出。Yang 等[12]进行了分级过滤器的除尘实验,上、下层分别填装轻而大和重而小的滤料。实验结果表明,在相同的床层压降下,分级过滤器的容尘能力是单层过滤器的10 倍。Shi 等[13]通过实验研究了上层膨胀珍珠岩和下层细砂组成的分级过滤器的过滤性能,结果发现分级过滤器的压降增长率与单层粗滤料过滤器基本相同,且远低于单层细滤料过滤器的压降增长率。
综上所述,可发现前人对于分级过滤的研究主要集中在实验层面,而杂质颗粒在过滤器内的沉积分布无法通过实验方法准确获得。本文利用CFDDEM 耦合方法,构建不同滤层结构的三维过滤器模型,获取颗粒沉积分布结果以辅助解释实验结果。
1 实验描述
图1 为颗粒层过滤实验装置简图,包括原料液供应和控制系统、输送原料液的泵系统、颗粒过滤系统。充分搅拌的原料液通过泵系统输送至滤层总高为40 mm 的过滤器的入口,随后原料液流经床层,未被收集的颗粒从过滤器出口逃逸。
实验中使用的滤料为α-Al2O3,并采用分级法进行填装。上层填充的粗滤料(记为D1)粒径为4 mm,下层填充的细滤料(记为D2)粒径为2 mm。图2 所示为5 种不同滤层结构的颗粒层过滤器,其中Ⅰ、Ⅴ为单层过滤器,Ⅱ、Ⅲ、Ⅳ为分级过滤器。利用流量计测量表观过滤速率(u),并分别控制表观过滤速率为50、100、150、200、250 mm/s。原料罐内料液的密度近似为1 000 kg/m3,动力黏度为0.001 Pa·s。常规的固液颗粒层过滤器中颗粒的体积分数在0.01%以下[14],本文中颗粒体积分数为0.005 6%,质量浓度控制在180 mg/L。进入过滤器的杂质颗粒通过细筛分获得,直径约为0.4 mm。每次实验在20 ℃的室温下重复3 次,以尽量消除偶然性。
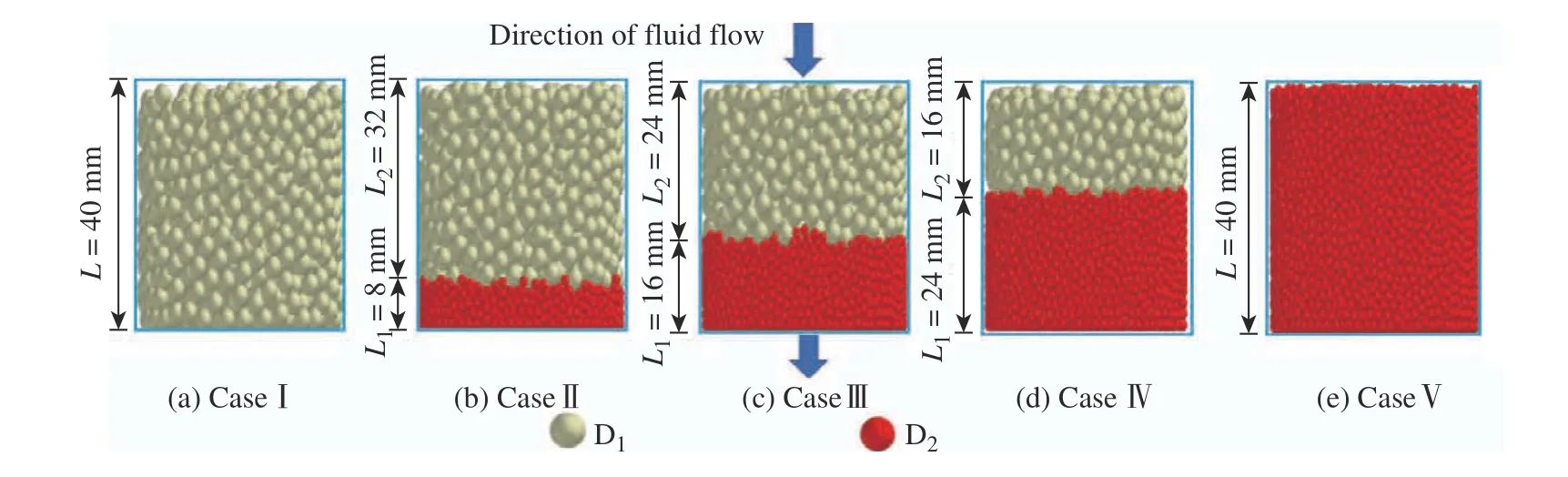
图2 不同滤料填装方式的过滤器Fig.2 Filters with different granular packing methods
2 数值方法和模型描述
2.1 数值方法
2.1.1 流体相控制方程 选取Eulerian 模型描述流体相的行为变化,并在控制方程中引入了过滤器的床层空隙率ε,实现流体相和离散相的双向耦合,以考察颗粒沉积对于过滤的影响。流体相的控制方程如下:
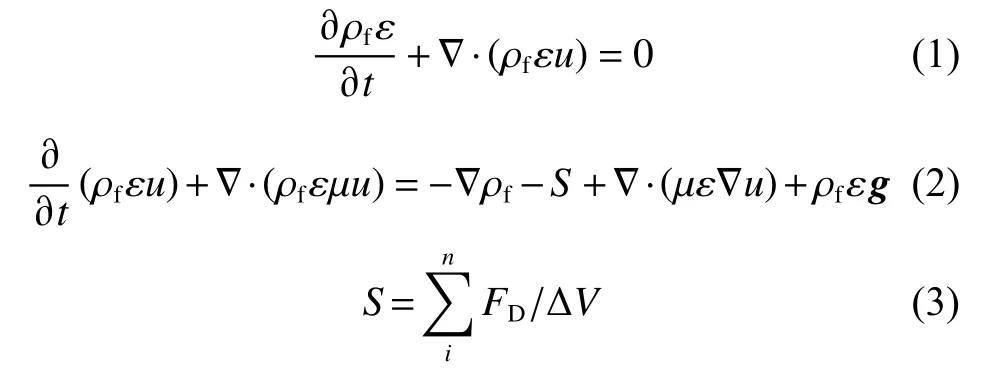
其中:ρf是流体密度;g是重力加速度;μ是流体黏度;S是作用在网格单元体积内的阻力FD的总和,ΔV表示网格单元体积。
流体在颗粒床层内的流动状态主要取决于床层雷诺数Re[15]:

其中:ρ为颗粒密度,D是颗粒直径,v是水流平均速率,α为滤料形状系数。当Re>2 时,流体流动状态为湍流。
根据式(4),若视颗粒为球体,则层流临界速率(Re=2 时的水流平均速率)为0.003 43 m/s。由于在文中最小表观过滤速率为50 mm/s,因此选择湍流模型。采用SSTk-ω模型描述介质空隙间湍流的影响,湍流动能k和比耗散率ω的方程分别为[16-17]:

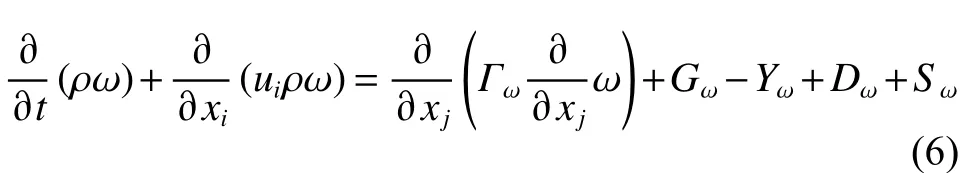
其中:xi、xj分别为i、j方向上的坐标值;Γk和Γω为湍流模型的有效扩散项;Gk为湍流动能;Gω代表ω方程;Yk和Yω表示湍流模型的发散项;Dω表示正交散度项;Sk和Sω由用户自定义。
2.1.2 固体离散相模型 在过滤过程中,由于颗粒与颗粒、滤料和流体相间作用力的存在,使得颗粒发生迁移,迁移轨迹通过Lagrange 方法求解。通常微米级颗粒才需要考虑非接触力,而本文中模拟涉及的颗粒粒径远大于微米级,所以不考虑非接触力的影响。颗粒间的接触力则利用Hertz-Mindlin 模型[18]计算,并表示为非线性的软球模型。在流体相中,颗粒的迁移运动方程如式(7)、式(8)所示:

其中:mp、up、ωp、fn、ft和Tp分别表示颗粒的质量(g)、速度(m/s)、角速度(rad/s)、法向碰撞力(N)、切向碰撞力(N)、碰撞力矩(N·m);Ip是颗粒的惯性矩(m4);Fg和fD(u-up)分别是颗粒的重力(N)和流体对于颗粒的阻力(N),fD表示为:

其中:ρp是颗粒密度;CD是非线性阻力系数,表达式如下:
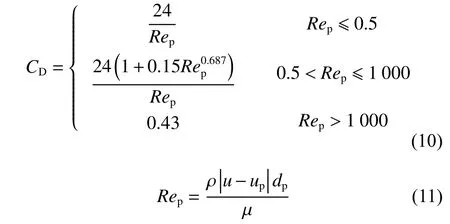
有关颗粒之间力的详细计算,可参阅文献[19]。
2.1.3 耦合计算方法 在CFD-DEM 双平台数值模拟过程中采用Eulerian 耦合法,其不仅考虑液固两相间的动量交互过程,同时也考虑颗粒对流场的影响[10]。DEM 平台选用EDEM (V 2018),CFD 平台选用Fluent (V 16.0),耦合流程由编译的UDF (User-Defined Function,用户定义函数) 加载。
图3 为CFD-DEM 耦合流程图,首先在Fluent 中初始化流场并进行零时刻流场数据的计算,随后将流场数据传输至EDEM 中,并利用Hertz-Mindlin 模型计算颗粒受到的曳力等所有接触力,由此计算颗粒速度等信息;将作用力等信息通过耦合程序传输至Fluent 中进行下一时间步长流场数据的计算,直至达到目标模拟时间。计算流场的时间步长取为3×10-4s,为准确获取颗粒接触力的信息,EDEM 时间步长设置为3×10-6s。本文的计算在Intel(R) Core(TM) i7-9750H CPU @ 2.60 GHz (6 核心,16 GB 内存)上进行,计算平均时长为60 h。

图3 CFD-DEM 耦合流程图Fig.3 Flow chart of the CFD-DEM coupling
2.2 过滤模型
图4 所示为过滤器的几何模型(以过滤器Ⅳ为例)及其边界条件,模型整体是半径为25 mm 的三维圆柱,DEM 计算域的高度为40 mm。滤料由EDEM中的“颗粒工厂”在DEM 计算域内随机生成并快速堆积。计算域底部的交织滤网在支撑滤料的同时保证杂质颗粒都能通过。流体的入口和出口分别采用速度进口和压力出口,进口速率与实验保持一致。为了保持进口速度的稳定,并避免流体从出口回流,分别对模型的进口和出口区域进行了加长处理。颗粒由颗粒入射面进入,并从压力出口边界离开模拟区域。模型的壁面设置为静止且无滑移,模拟参数如滤料粒径和杂质颗粒粒径等均与实验条件相同。表1 所示为模拟所用物性参数。结构化网格被应用于划分Fluent 中过滤器模型的网格,网格数量为2 261。为了保证数值结果的准确性,EDEM 中过滤器模型的网格数量分别依次划分为982 600、1 706 256、3 342 336 和7 860 800。模拟结果显示,网格数量为3342 336 和7 860 800 的模型所得到的初始压降值和过滤效率均非常接近。因此,从数值结果的精度和计算机资源两方面考虑,EDEM 中网格数量划分选取3 342 336。

表1 模拟物性参数Table1 Physical parameters in the simulation

图4 过滤器模型及其边界条件Fig.4 Filter model and its boundary conditions
在颗粒层过滤实验中,过滤效率 ( η) 定义为:

其中:Cin为进口颗粒质量浓度,mg/L;Cout为出口颗粒质量浓度,mg/L。假设所有颗粒的物性参数相同并视为球体,则可采用颗粒数目代替颗粒质量浓度的方法计算过滤效率。而初始过滤效率定义为滤料处于干净状态下的过滤效率。
Ergun 方程[20]可用于预测颗粒床的初始压降( Δp):

其中: 为颗粒球形度;de为颗粒体积等效直径,m。
虽然不存在计算容垢量的公式,但很显然,颗粒沉积均匀度(λ)越大,则相同质量的颗粒沉积引起的压降增量越小,过滤床的容垢能力就越高。因此,本文采用沉积均匀度来评价过滤器的容垢能力。
图5 所示为颗粒层过滤器分节示意图。将过滤器沿着过滤方向分为20 节,颗粒沉积均匀度由式(14)定义:
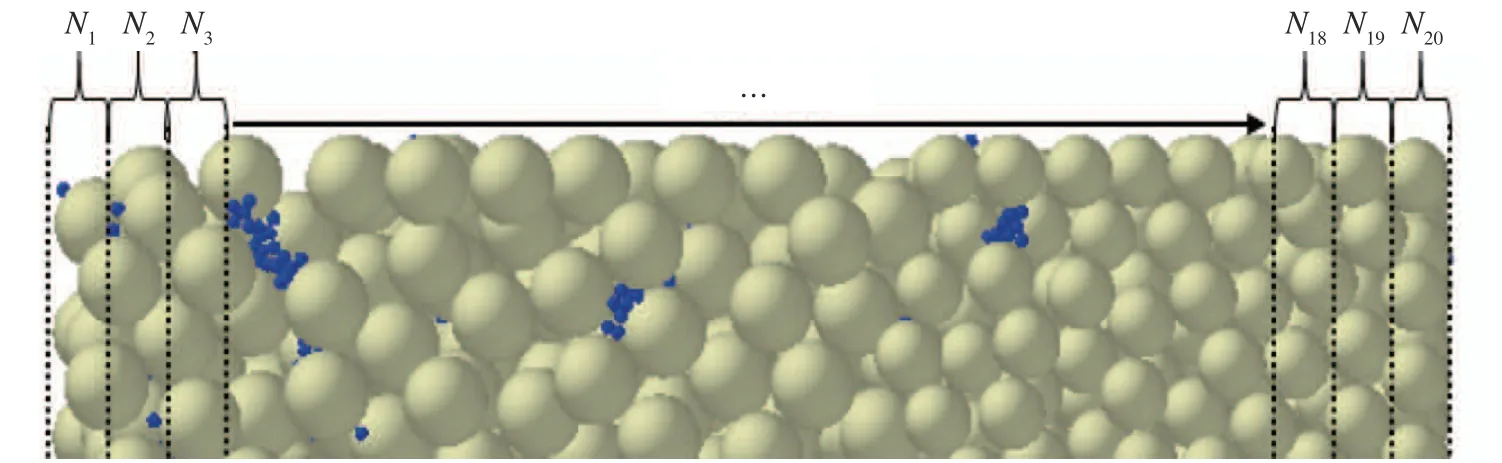
图5 颗粒层过滤器分节示意图Fig.5 Schematic diagram of granular bed filter segmentation

其中:n为床层节数,Ni为每一节床层中沉积的颗粒数目,Nave为沉积颗粒数目的算术平均数。颗粒沉积越均匀,λ越趋向于1。每一节床层中的颗粒沉积分数( ϕ )定义为:

3 结果与讨论
3.1 初始压降与过滤效率
图6(a)所示为过滤器Ⅰ、Ⅳ和Ⅴ的初始压降结果。从图6(a)可知,压降模拟结果与实验结果基本一致,但后者数值略大,这可能是因为在实验过程中,流体流过过滤器壁面时,由于摩擦而产生了微小的压降。在相同过滤速率下,过滤器Ⅳ的压降仅为过滤器Ⅰ和Ⅴ压降之和的一半左右。
图6(b) 所示为表观过滤速率为50 mm/s 时,不同床层深度下过滤器V 的初始压降模拟结果和Ergun 方程结果之间的比较。Ergun 方程允许的误差范围为±25%,虽然模拟计算得到的压降值稍大,但两者之间的偏差仍处于有效范围内。
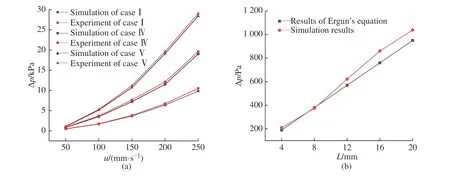
图6 (a)不同过滤器初始压降的实验值和计算值比较;(b)不同床层深度下过滤器Ⅴ的初始压降Fig.6 (a) Comparison of initial pressure drop of different filters between experiment and simulation; (b) Initial pressure drop under different bed depths of filter with case Ⅴ
图7(a) 所示为不同表观过滤速率下过滤器Ⅰ、Ⅱ和Ⅴ的初始过滤效率变化,黑点和红点分别代表实验和计算结果。由图可得,模拟结果与实验结果具有良好的一致性。过滤器Ⅰ的过滤效率明显小于其他滤层结构的过滤器。如当表观过滤速率为50 mm/s时,过滤器Ⅰ的过滤效率约为70%,而其他滤层结构过滤器的过滤效率均约为90%,说明采用分级填料可以大幅提高过滤效率。
很显然,通过模拟分析可便捷地得到过滤效率随床层深度的连续变化。图7(b)所示为表观过滤速率为50 mm/s 时,不同床层结构和不同床层深度下的过滤效率模拟值。可以看出,当过滤器Ⅴ的床层深度约为24 mm(称为“转折点”)时,其过滤效率达到最大值并保持稳定。过滤器Ⅲ和Ⅳ的转折点分别约为32 mm 和28 mm;而过滤器Ⅰ和Ⅱ的转折点大于40 mm。综上分析可知,下层细滤料层深度的增加使转折点提前出现。

图7 (a)不同过滤器过滤效率的实验值和模拟值比较;(b)不同过滤器不同床层深度下的过滤效率模拟值Fig.7 (a) Comparison of filtration efficiency of different filters between experiment and simulation; (b) Simulation results of filtration efficiency under different bed depths of different filters
过滤器的综合性能由过滤效率和压降共同决定,不同滤层结构过滤器的综合评价指标(Y) 根据式(16)定义[21],计算得到的Y值如图8 所示,可见在不同表观过滤速率下,分级过滤器相比于单层过滤器具有更高的Y值,即分级过滤的综合过滤性能最佳。
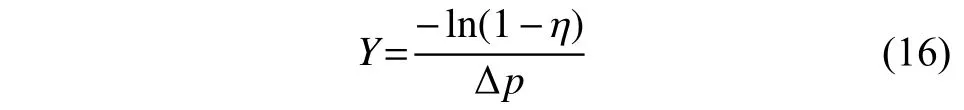

图8 不同床层结构过滤器的Y 值Fig.8 Y Value of filters with different bed structures
3.2 颗粒沉积形貌
杂质颗粒沉积形貌的结果更加直观,可加深对过滤现象的理解。图9 所示为当表观过滤速率为200 mm/s、过滤时间为10 s 时,过滤器Ⅱ和Ⅴ的细滤料层表面的颗粒沉积形貌,可发现两者的颗粒沉积图是近似的,过滤器Ⅴ的细滤料层表面沉积的杂质颗粒数目大于分级过滤器Ⅱ的细滤料层表面杂质颗粒数。由此可以推断,分级过滤可以使杂质颗粒部分容纳在粗滤料层中,提高了床层容垢量。
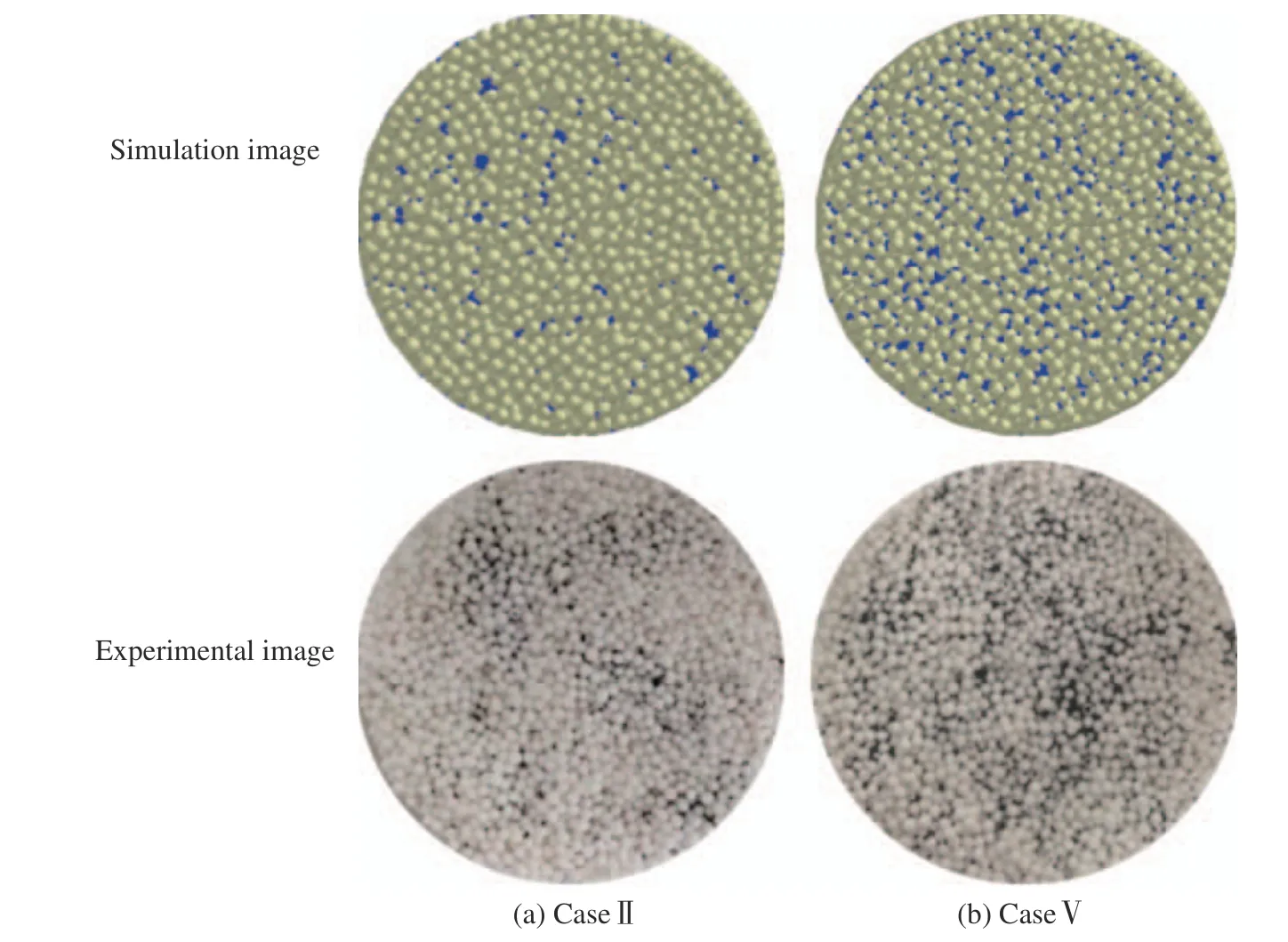
图9 细滤料层表面的颗粒沉积形貌Fig.9 Deposition morphology on the surface of fine granular layer
图10 所示为当表观过滤速率为50 mm/s,过滤时间为10 s 时,模拟所得同一纵截面下过滤器Ⅰ、Ⅱ和Ⅴ的颗粒沉积图。可以看出,过滤器Ⅴ近入口处及过滤器Ⅱ上、下层滤料的分界处形成明显的团聚沉积结构。这可以从惯性机制[6]的角度进行解释,当滤料粒径为2 mm、过滤速率为50 mm/s 时,斯托克斯数(St)约为1.5,颗粒的惯性发挥作用,使得颗粒容易偏离流体流向,其运动轨迹与滤料表面相交的几率增大,颗粒发生高频率碰撞并被快速捕集。较高的捕集几率促成颗粒间的架桥现象,从而形成团聚结构,其可视为新的“过滤器”来截留颗粒,因而大幅降低了滤层表面的空隙率,也解释了图6(a)中过滤器Ⅴ的压降远高于其他过滤器的原因。
由图10 可知,过滤器Ⅰ及过滤器Ⅱ的上层滤料表面并未出现明显的团聚结构。相比于过滤器Ⅴ,过滤器Ⅰ较大的滤料粒径使得惯性作用明显减弱,颗粒更容易随着流体流线运动而被夹带至床层的深处,使得颗粒的分布较为均匀。此时可考虑拦截机制[22],而只有当颗粒的轨迹恰好落在滤料表面到滤料半径的流线范围内时,拦截机制才对颗粒迁移产生影响,颗粒才会被滤料表面截留,因此难以形成团聚结构。
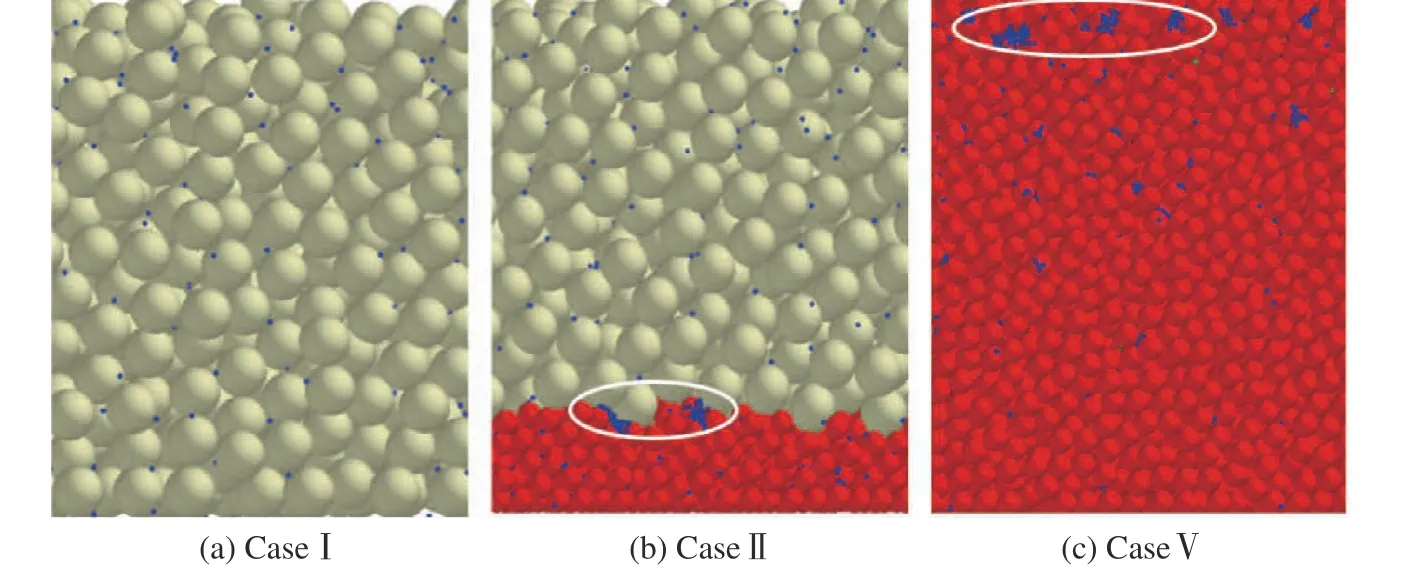
图10 不同过滤器同一纵截面的颗粒沉积形貌Fig.10 Particle deposition morphology in the same longitudinal section of different filters
3.3 颗粒沉积均匀度
从杂质颗粒沉积形貌来分析颗粒沉积分布仅是定性分析,通过EDEM 的“group bin”后处理功能可得到不同床层节数上滤料表面及间隙所沉积颗粒的数量,从而定量分析颗粒沉积均匀度。当表观过滤速率为200 mm/s、过滤时间为10 s 时,不同床层节数上的杂质颗粒沉积分数如图11(a)所示。对于过滤器Ⅴ,杂质颗粒的沉积分数随着床层节数的增大而明显减小。可以看出,前5 节床层的颗粒沉积分数之和达到了71.2%;当床层节数达到10 左右时,颗粒沉积分数就几乎降低为0,后半段床层的颗粒沉积分数之和仅为8.4%,这意味着过滤器Ⅴ收集的颗粒几乎都容纳在过滤器的前端部分。过滤器Ⅰ中每一节床层的颗粒沉积分数基本都为0.05~1.00。对于过滤器Ⅱ,当床层节数小于16 时,每一节床层的颗粒沉积分数相差不大,提供较高容垢量;而当在床层节数为17 时,颗粒沉积分数显著增大,表明颗粒收集量快速增加,保证了分级过滤器的过滤效率。

图11 颗粒的沉积分布Fig.11 Particle deposition distribution
图11(b)定量分析了不同滤层结构下颗粒沉积均匀度的变化。结果表明,沉积均匀度随表观过滤速率的增加而增加。如当过滤速率从50 mm/s 增加至250 mm/s 时,过滤器II 的沉积均匀度由0.73 增加到0.84。这是由于过滤速率的增大使滤料表面已沉积颗粒的剥离行为更显著。过滤器V 的沉积均匀度明显低于其他4 种滤层结构过滤器。当表观过滤速率为200 mm/s时,过滤器II 的沉积均匀度比过滤器V 高59.4%;当滤层结构由V 变化至IV,沉积均匀度增加0.217,而从IV 变化到I,沉积均匀度仅增加0.103。
引入分级过滤器的平均滤料直径(Dave),并定义为:

式中:D1、D2分别为上、下层滤料直径;L1、L2分别为上、下层滤料层厚度。
对影响沉积均匀度的各个参数进行量纲分析,通过白金汉定理和量纲一致性,沉积均匀度可表示为:
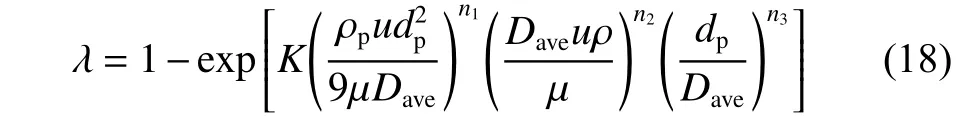
利用1st Opt 软件进行多元非线性回归分析,得到在50 mm/su< 250 mm/s, 2 mmDave<4.0 mm 范围内,沉积均匀度的关系式如下:

图12 对比了沉积均匀度的预测结果( λpre:)与计算结果( λcal:)。由图可知,沉积均匀度的模拟结果与回归方程值吻合良好,偏差小于5%,说明拟合具有足够的精度。

图12 沉积均匀度的预测结果和计算结果的对比Fig.12 Comparison of deposition uniformity between predicted and calculated results
4 结 论
采用CFD-DEM 耦合方法,对不同滤层结构的颗粒层过滤器进行固液分级过滤的数值模拟研究,主要结论如下:
(1) 过滤效率的模拟计算值与实验值吻合良好,压降值的偏差在Ergun 方程允许误差范围内。过滤效率和压降随床层深度的增加而增加,当床层深度增大至转折点时,过滤效率基本不变,且随着下层细滤料层深度的增加,转折点提前出现。
(2) 过滤器的容垢能力由颗粒沉积均匀度表示。颗粒沉积均匀度随表观过滤速率的增大而增大,滤层的分级填装使得杂质颗粒在床层中的沉积均匀度大幅提升。通过拟合回归得到不同滤层结构过滤器沉积均匀度的关联式,且偏差小于5%。
(3) 杂质颗粒的沉积分布表明:单层细滤料过滤器由于较强的颗粒惯性作用而形成颗粒团聚结构,颗粒沉积主要发生在近入口处,容垢量较低;分级过滤器的上层粗滤料截留了部分的杂质颗粒,在保证过滤效率的前提下,降低了过滤器的压降,同时提高了容垢量。
