基于统计信息反馈的分步多目标优化

王学武， 谢祖洪， 周 昕， 顾幸生

（华东理工大学能源化工过程智能制造教育部重点实验室，上海 200237）

一个连续的非约束多目标问题（Multi-Objective Optimization Problem, MOP）拥有多个相互矛盾、相互影响的目标，且这些目标需要同时被优化[1]。多目标优化问题是工业生产和日常生活中经常遇到的问题，它遵循效益最大化和成本最小化等基本原则。效益可能是多种效益，即经济效益、社会效益等；成本或损失也可能包括生产成本和非生产成本，甚至可能是环境污染这类的其他目标。以焊接路径规划为例，焊接目标通常有焊接路径长度、能耗、变形等。目前多目标优化问题的研究已引起了广泛的关注，被应用于任务调度、工程设计、系统控制、焊接路径规划等众多领域。

假设x,y∈Ω 是某一多目标优化问题的任意两个解，当满足fi(x)fi(y), ∀i∈1,2,···,m时，我们定义x支配y，即x≻y；其中 Ω ⊆RD表示决策空间，x=(x1,x2,···,xD) 表示由D个参数组成的决策变量，F:Ω →Rm由m个 目 标 函 数 (fi(x),i=1,2,···,m) 构成， Rm表示目标空间。在目标空间中，如果没有解可以支配x∗，则称x∗为Pareto 最优解，也被称为非支配解，所有的Pareto 最优解组成的集合称为Pareto 最优解集。将Pareto 最优解集中的所有Pareto 解映射到目标空间，得到Pareto 前沿(Pareto Front, PF)。多目标进化算法(Multi-Objective Evolutionary Optimization Algorithm，MOEA) 致力于在真实PF 附近获得均匀分布的Pareto 最优解集[2]。

多目标进化算法一直致力于获得收敛性和分布性俱佳的非支配解集[2]。根据不同的进化机制，多目标进化算法大致分为3 类[3]：基于分解的MOEAs、基于支配关系的MOEAs、基于指标的MOEAs。基于分解的MOEAs 利用聚集函数将多目标优化问题转化为多个单目标优化子问题，再根据在超平面上均匀分布的参考向量来选择优秀个体。Zhang 等[4]基于上述分解思想提出了MOEA/D 算法，引起了广泛关注。在此基础上改进的算法还有MOEA/D-DE[5]、MOEA/D-AS[6]、MOEA/D-AAP[7]。基于支配关系的MOEAs 结合非支配关系和小生境技术选择后代解集，主要算法有NSGA-Ⅱ[8]、SPEA2[9]、PESA-Ⅱ[10]。基于指标的MOEAs 利用性能指标指导算法搜索过程和后代选择过程，主要算法有IBEA[11]、SMSEMOA[12]、HyPE[13]。

除了传统的MOEAs 外，还有很多学者提出了综合性算法来增强收敛性和分布性。Deb 等[14]结合非支配排序和参考点选择后代解，将算法拓展用以解决高维多目标优化问题。Sato 等[15]通过对传统给予惩罚的边界交叉法(Penalty-Based Boundary Intersection Approach，PBI) 和权重向量法(Weighted Sum，WS)进行拓展，提出了一种新的聚合函数，即反转PBI(Inverted Penalty-Based Boundary Intersection，IPBI)。Trinadh 等[16]提出了一种基于指标(ISDE+) 的多目标进化算法，该指标计算个体之间的欧氏距离用以估计个体在种群中的密度。Sun 等[17]提出了一种新的存活时间指标来指导差分进化重组算子，以此平衡算法中个体的开发性和勘探性。

传统的多目标进化算法通常同时考虑解的收敛性和分布性，在算法搜索初期会生成大量的支配解，造成计算资源的浪费。因此，本文提出了基于统计信息反馈的分步多目标优化算法（A Stepwise Multi-Objective Evolutionary Optimization Algorithm Based on Statistical Feedback Information，SFI-SMOEA ）。SFI-SMOEA 分为3 个阶段，第一阶段主要进行单目标最优值探索；第二阶段主要进行Pareto 前沿的探索；第三阶段进行局部优化，加强分布不均和收敛性不足的部分区域的探索。在算法搜索后期，性质差异过大的两个亲本生成的解极有可能是支配的，也会造成计算资源的浪费；于是SFI-SMOEA 按照目标函数值将性质差异较大的解分为不同群体，分别对不同群体的解进行聚类分析，对优秀个体进行评估；再根据评估信息指导种群亲本选择过程，保证优质解的交配次数；根据上一次迭代信息生成偏好的优质解，并调整解集结构。

1 SFI-SMOEA 算法框架

传统的多目标进化算法[4,8,10]通常协同考虑全局的收敛性或者多样性，可能导致算法对于单目标极值探索的不足，而且在搜索初期会生成大量支配解，造成计算资源的浪费。SFI-SMOEA 将整个优化算法分为3 个阶段：

（1）单目标探索阶段。在此阶段，放弃对整个Pareto 前沿的探索，分别对优化问题的多个目标进行相对独立的探索，使其快速找到每个单目标的最优解。

（2）单目标到多目标的过渡阶段。在单目标探索阶段结束后，解围绕在各个目标的最优值附近。此阶段的主要任务是加强对整个Pareto 前沿的探索，尤其针对部分未覆盖区域，这是为了促进算法的分布性。

（3）群体划分局部优化阶段。经过第一、二阶段的探索，形成基本的Pareto 前沿，但是局部收敛性不足。因此，第三阶段的主要任务是根据目标函数值进行群体划分，利用反馈信息加强局部Pareto 前沿的开发。在迭代过程中，根据目标函数值将所有解划分为不同区域；然后反馈各个区域解的分布情况，在稀疏区域生成更多解，进一步增强算法搜索能力。

SFI-SMOEA 的每个阶段包含不同的任务，整个框架如算法1 所示。其中，小生境保留技术参照NSGA-III[14]，包括非支配排序、解与参考点的关联操作、根据关联操作选择下一代种群。

算法1 SFI-SMOEA 算法流程

1.1 单目标探索阶段

在单目标探索阶段，分别对每个目标最优值进行探索，期望尽快找到每个目标的最优值。在此阶段，将多目标优化问题转化成m个单目标优化问题，并利用改进的单目标遗传算法进行求解。

1.1.1 挑选精英个体 在传统遗传算法[18]中，亲本的选择是根据适应度进行的，适应度高的解有更大概率被选为亲本。当算法进行了一段时间后，解空间内解的相似度很高，进行交配的领域变小，可能导致算法陷入局部最优。在处理此类问题时，有学者提出采用事件触发机制[19]增强算法跳出局部最优的能力。对于遗传算法求解单目标优化问题而言，一方面我们希望优秀个体可以获得更大的交配机会；另一方面，我们也希望保持种群的多样性，避免算法陷入局部最优。基于以上分析，将解按照单目标适应度进行排序，挑选出部分优秀个体建立外部档案（Xg），其中每个目标优秀个体的数目根据种群大小和待优化问题的目标维度确定。通过对部分个体进行评估，确定优秀个体的交配次数，保证优秀个体的基因得以保留；然后删除种群中多余的重复解，随机生成新的解，直到满足种群数目要求。

1.1.2 对优秀个体进行相似性和离散程度的评估由于对整个种群中的每一个个体进行价值评估计算较为复杂，因此只对通过适应度值挑选出的优秀个体进行价值评估。对优秀个体进行相似性和离散程度的统计，采用基于相关性的密度估计指标ICDE，类似于统计学中相关系数的计算[20]，如式(1)所示。

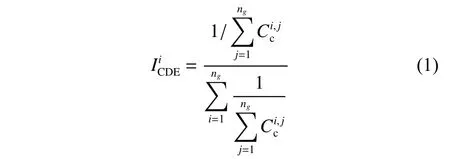
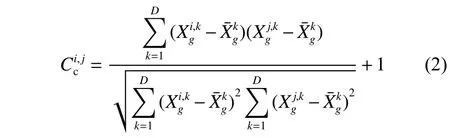
1.1.3 根据评估结果指导亲本选择 设计智能优化算法的关键是平衡算法在寻优过程中的开发性和探索性。本文利用ICDE指导亲本选择过程，从而实现开发性和探索性的平衡。由1.1.2 节可知，越大，表示个体i与其他个体的相似度越低，离散度越高。此时，说明个体i具有很高的开发价值，应该给个体i更多的配偶，从而加快算法向个体i收敛。反之，说明算法可能陷入局部最优。此时应该增强算法随机性和解空间领域的大小，减少优秀个体的交配次数，删除种群内多余重复解，借此搜索到表现更优的个体，从而增强算法的“爬山”能力。其中优秀个体的交配次数如式(3)所示。

式中：N为种群大小；表示向下取整； α 表示对优秀个体的重视程度， α 越大，优秀个体交配次数越多，本文设定 α =3 。由于亲本每次交叉可以获得两个后代解，因此将交配次数除以2。

根据评估结果指导亲本选择过程的伪代码如算法2 所示，即基于优秀个体的亲本选择算子(Parent Selection Operator Based on Excellent Individuals，EIPS)。

算法2 基于优秀个体的亲本选择算子(EIPS)

第一阶段单目标探索阶段包括挑选优秀个体、对优秀个体进行相似性和离散程度的评估、根据评估信息指导种群亲本选择过程。图1 所示为部分三维测试案例第一阶段解的分布情况，可以看到其中的大部分解都围绕在各个目标最优值附近。

图1 部分三维测试案例第一阶段解集分布情况Fig.1 Distribution of solution sets in the first stage of some 3-objective test cases

1.2 单目标到多目标的过渡阶段

过渡阶段的首要任务是使种群初步收敛到Pareto 前沿上，其中包括对个体进行群体划分，根据划分结果指导亲本选择过程。但是在单目标探索结束后，种群中个体大多集中在各个目标的最优值周围，因此需要对种群中的个体进行聚类分析，再根据分析结果合理地分配交配资源，使其快速收敛到Pareto 前沿。

1.2.1 根据目标函数值划分种群 整个种群的个体差异较大，不便于进行分析，因此根据个体的目标函数值将其划分成不同群体。同一群体内，个体性质相近，而与其他群体中的个体性质差异较大。划分群体的个数取决于待优化问题的目标维度。在欧式空间中划分区域，本质是边界的确定，本文设置的边界是过原点的向量。对于M维的优化问题，边界向量的生成采用的是边界交叉构造权重向量的方法[21]。在标准超平面上，按照式(4)生成均匀的参考点。每一维目标被均匀地分割成p份，因此边界向量的个数为 n umw。为了减少复杂度，本文设定p=2 。对于M维优化问题，解被分为(M+1)个群体。

图2 所示为三维优化问题的种群划分示意图。每一维目标被均匀地分为2 份；共有6 个权重向量w1=(0,0,1) 、w2=(0.5,0,0.5) 、w3=(0,0.5,0.5) 、w4=(1,0,0) 、w5=(0.5,0.5,0) 、w6=(0,1,0) 。将 目 标 函数值空间分为4 个区域：w1、w2、w3围成的空间为1 号区域；w2、w3、w5围成的空间为2 号区域；w2、w4、w5围成的空间为3 号区域；w3、w5、w6围成的空间为4 号区域。

图2 三维优化问题的种群划分Fig.2 Population division of for 3-objective optimization problems

1.2.2 根据种群划分结果指导亲本选择 种群类别划分的区域是参考权重向量生成方式进行的，理想情况下，每个区域内的个体数由被优化问题的Pareto分布决定。由于在单目标探索阶段结束后，解大都分布在各个目标最优值周围，可能导致部分区域解的个数很少，甚至有些区域没有解，此时应该加大此区域中解的生成，从而使得解尽快收敛到Pareto 前沿上。对不同类别的个体数进行统计，再根据统计结果确定亲本选择的概率，从而实现对各个区域个体数的控制。其中，在同一区域内进行亲本选择的概率Ps由式（5）计算：

其中：ns为同类别个体的数量；N为种群中个体的数量；A为控制参数，本文中A=0.5。同类别个体的数量越多，即ns越大，选择同类别个体作为亲本的概率越小，后代生成相似性质解的概率越小，从而实现对各个群体个体数量的控制。根据种群划分结果指导亲本选择过程的伪代码如算法3 所示，即基于种群划分的亲本选择(Parent selection operator based on population division，PDPS)。

算法3 基于种群划分的亲本选择(PDPS)

1.3 群体划分局部优化阶段

经过第一、二阶段的优化后，种群基本收敛到Pareto 前沿上，只有少数区域收敛性不足和解分布不均匀。本阶段的首要任务是对种群个体进行群体划分，分别对各个群体的解进行聚类分析，选择其中表现优异的个体作为领导者；利用领导者对群体进行收敛性和分布性评价，然后根据评价结果指导亲本选择过程，从而实现收敛性的优化及对分布性的控制。

1.3.1 聚类分析 将种群划分为若干区域后，同一区域内解的性质相似，便于统计分析。分别对每个区域内的解进行线性回归分析[22]，模拟出近似的Pareto 前沿，计算解到模拟Pareto 前沿的距离，即。如图3 所示，阴影部分表示通过线性回归获得的近似Pareto 前沿。个体的优劣是通过它的收敛性和分布性决定的，对于最小化问题而言，优秀个体在模拟Pareto 前沿的下方，离Pareto 前沿越远，说明此个体的收敛性越强。反之，如果个体在模拟Pareto 前沿的上方，说明此个体的收敛性较差。按照1.1.2 节所述方法，对同区域内的个体进行相似性和离散程

图3 三维PF 线性拟合Fig.3 Linear fitting of 3-objective PF

油田配电网变压器节能改造的研究…………………………………………………………………………………陈亚莉（3.30）

1.3.2 根据聚类分析结果指导亲本选择 经过实验发现，性质差异较大的两个解生成的后代很大概率是支配解，造成计算资源浪费，不能达到使Pareto 收敛的要求。为了避免此类情况，在群体划分局部优化阶段，个体只与同区域或者相邻区域个体交配。以如图1 所示的三维问题为例，区域1 和区域2 相邻，区域3 和区域2 相邻，区域4 和区域2 相邻，区域2 和区域1、3、4 都相邻。区域1 中的个体只与区域1、2 中的个体进行交配。通过聚类分析选出各个区域的优秀个体，优先给此类个体分配配偶，然后在同一区域或者相邻区域随机分配配偶，直到交配池数量要求。配偶选择过程如算法4 所示，即基于领导者的亲本选择(Parent selection operator based on leaders，LPS)。

算法4 基于领导者的亲本选择(LPS)

2 仿真实验与分析

为了验证本文算法的性能，选取DTLZ(DTLZ1～DTLZ7)[23]和WFG(WFG1～WFG7)[16]系列测试案例进行实验，共14 个测试问题，每个测试问题分别测试3、5、8、10 个目标，并与NSGA-III[14]、A-NSGAIII[24]、MOEA/D-M2M[25]、ISDE+[16]等多目标进化算法进行对比。对于模拟二进制交叉和多项式变异的参数，本文进行统一设定。交叉概率pc=1 .0，交叉分布指数 ηc=20 ；变异概率pm=1/D(D为变量维度)，变异分布指数 ηm=20 。

图4 示出了部分测试案例在1 次运行中通过SFI-SMOEA 获得的解的分布情况。从图4 中可以看出，这些测试案例的真实PF 复杂而多样(包括凹凸不一、有多个局部前沿、各个目标比例不一、退化等)。在这些测试问题中，SFI-SMOEA 均能获得收敛性和分布性俱佳的Pareto 解集。

图4 SFI-SMOEA 下部分测试案例的解分布Fig.4 Solutions distribution of some test cases by SFI-SMOEA

为了比较各个算法的性能，采用两个综合评价指标，即反转世代距离(Inverted Generational Distance,IGD)和超体积指标(Hypervolume, HV)[25]。IGD 指标通过计算真实Pareto 解集中的个体(x∗)到算法所求的非支配解集中的个体(x)的平均距离(d(x∗,x) )得到，如式（6）所示：IGD 能综合反映MOEA 的收敛性和分布性，IGD 值越小，说明算法的综合性能越好。

表1 DTLZ 测试案例的HV 平均值（标准差）Table1 HV mean values (standard deviation) of DTLZ test cases

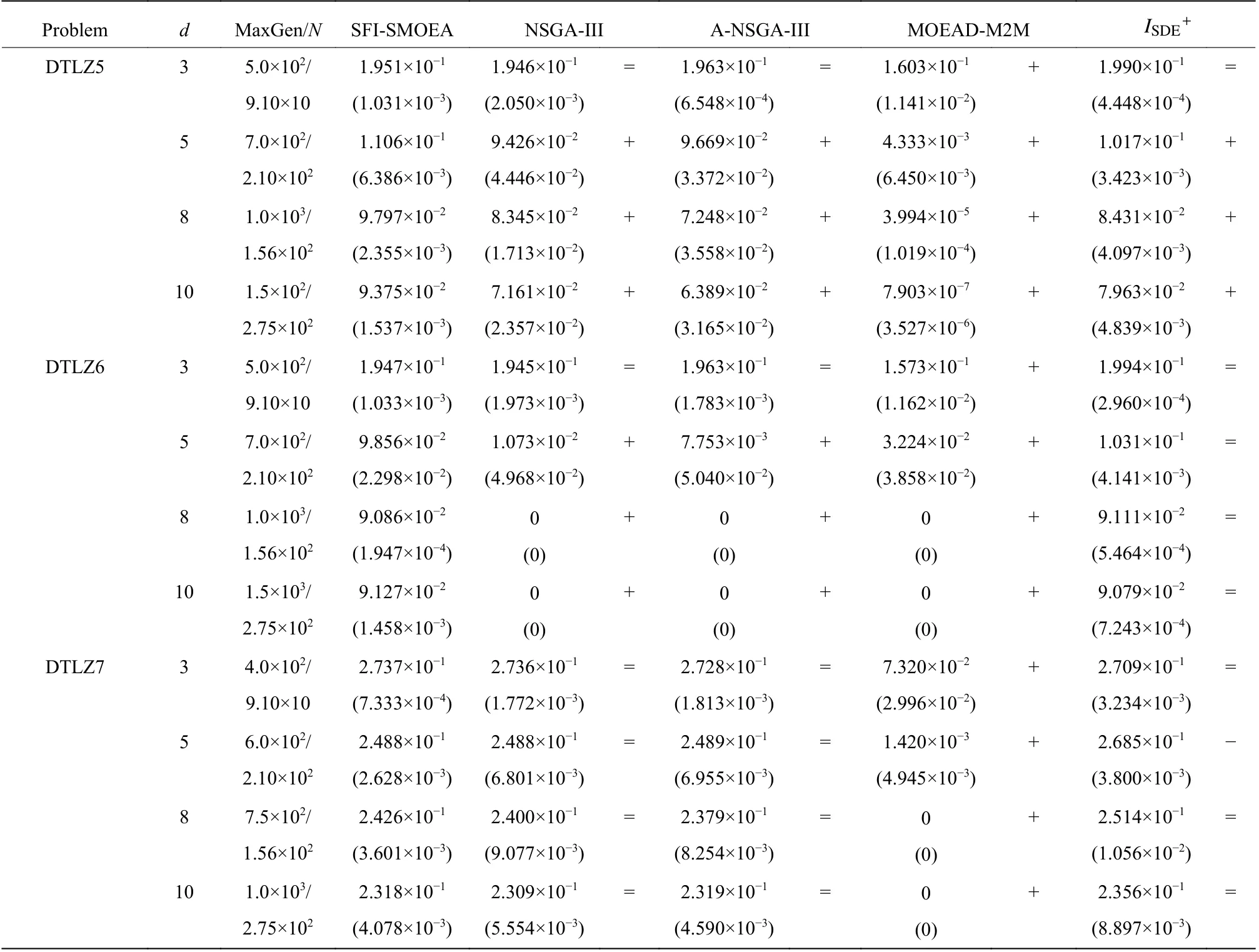
续表1

表2 WFG 测试案例的HV 平均值（标准差）Table2 HV mean values (standard deviation) of WFG test cases

续表2

在56 个测试问题(包括DTLZ 系列和WFG 系列)中，本文算法比NSGA-III、A-NSGA-III、MOEADM2M、ISDE+更好或者相似的比例分别为83.04%、82.14%、94.64%、68.75%。综合来看，本文算法在DTLZ 和WFG 测试问题上显著优于MOEAD-M2M，与NSGAIII 和A-NSGAIII 相似。

从各个测试案例的收敛情况来看，对于DTLZ4、WFG1、WFG2 等侧重分布性的多目标问题，SFISMOEA 性能比NSGA- III 算法差。

分析后发现，SFI-SMOEA 为了算法的收敛性，第一阶段只关注各个目标的最优值，相当于只考虑算法的收敛性，从而导致部分基因缺失，最终使得算法分布性性能下降。但是，对于侧重收敛性的问题，尤其是高维难收敛的问题，例如DTLZ3、DTLZ6、WFG3 等问题，SFI-SMOEA 的性能明显优于NSGAIII。针 对d≥8 时 的DTLZ6 和WFG3 问题，NSGAIII 和A-NSGA-III 算法不能收敛到真实Pareto 前沿附近，而改进后的算法能很好地处理这些问题。这得益于将算法分为3 个阶段，首先考虑优化问题各个目标的最优值，加强了算法的收敛性。

对SFI-SMOEA 和ISDE+进行对比分析后发现，SFI-SMOEA 和ISDE+算法的收敛性都比较好，针对DTLZ6 和WFG3 等难收敛的问题都能较好地收敛到真实Pareto 前沿附近。但是二者都存在分布性较差的问题，尤其针对WFG1、WFG4 这类问题。这是由于在算法搜索初期，两者都注重收敛性，导致部分基因缺失，表现为较差的分布性。SFI-SMOEA 在第三阶段加入了对优秀个体离散程度的评价，增大离散程度大的个体的交配概率，一定程度上加强了算法的分布性。

对WFG3 进行详细测试，进一步说明算法的性质。分别采用4 种对比算法(NSGA-Ⅲ、A-NSGA-Ⅲ、MOEA/D-M2M 和ISDE+)和SFI-SMOEA 在不同迭代次数下独立运行20 次，所测得的WFG3 的IGD平均值如图5 所示。在三目标情况下，本文算法和ISDE+表现最好，各类算法性能均有上限，在300 代左右达到最优。针对更高维目标，所有算法都在一定迭代次数后性能变差，尤其是MOEA/D-M2M。经过对WFG3 分析后发现，WFG3 的真实PF 通常为一条直线，随着算法进行迭代，会在远离真实PF 的地方生成许多非支配解。随着迭代次数的增加，不在真实PF 附近的非支配解个数增加，进而导致算法性能变差。在一定迭代次数(300 代左右)内，本文算法性能较优。随着迭代次数的增加，算法性能越来越接近NSGA-Ⅲ，这是因为算法的选择机制和NSGA-Ⅲ中采用的小生境技术一致。对于高维目标，ANSGA-Ⅲ算法表现优良，进一步说明参考点的自适应调节具有研究价值。

图5 不同迭代次数下5 种算法的IGD 平均值Fig.5 IGD mean values of five algorithms in different iterations

3 结 论

本文提出了一种基于统计反馈信息指导亲本选择的分布多目标进化算法（SFI-SMOEA）。在算法搜索初期，为了提升算法收敛性，致力于获得各个目标函数值的最优值。在算法搜索后期，通过对各个区域的解的分布情况进行统计分析，再根据反馈信息指导种群交配和选择，从而增强种群的分布性。将SFI-SMOEA 与多个多目标进化算法进行对比发现，SFI-SMOEA 能获得收敛性和分布性俱佳的Pareto 最优解集。尤其针对10 维目标的WFG3 之类的高维难收敛问题，SFI-SMOEA 展现了它的优先性和竞争力。

SFI-SMOEA 侧重于后代解的生成，新种群的选择策略参考原始的NSGA-Ⅲ中所提的小生境保存技术。在新种群的选择过程中，可能导致高质量的后代解被错误地删除。因此，新种群的选择策略非常值得深入研究。本文在选择新种群时，结合了非支配排序和参考点，但是由于参考向量或者参考点的生成都是在超平面上完成，只能保证这些点在超平面上均匀分布。映射到Pareto 前沿后，并不能保证每一个参考点都能找到至少一个解与之关联，也就是说参考点的分布与Pareto 前沿的分布无关，因此，可以进一步研究在有效的目标函数值空间生成均匀的参考向量或者参考点自适应的方法。