基于网格加速与顺序选取策略的图像匹配算法

江一苇，顾幸生

（华东理工大学能源化工过程智能制造教育部重点实验室，上海 200237）

自动驾驶、无人机、餐厅和医院的服务机器人等都需要对机器人本体进行实时定位，从而可以使机器人提供精准的服务。获取机器人位置与姿态的方法有激光、轮速传感器、惯性测量单元（Inertial MeasurementUnit，IMU）和视觉传感器等，而视觉传感器以其低廉的价格以及较高的性能被广泛应用于上述场景中[1-3]。

相较于其他的定位方式，视觉传感器尤其是双目相机最接近人类的实际视觉系统[4]。其定位的主要方法是利用相机对物体或者场景进行拍摄，对前后帧图像进行特征点与描述子的提取，然后对上一时刻与当前时刻两张图像的特征点进行匹配，以此估算特征点的运动，还原出相机本体在世界坐标系下的运动[5]。特征点匹配的精确程度极大地影响着相机运动的精度，如何进一步提升特征点的匹配精度是近几年的一个研究热点。主流的方法是针对特征点本身进行相关优化，例如：旋转不变性特征[6]（Oriented FAST and Rotated BRIEF，ORB），在FAST（Features fromAcceleratedSegmentTest）角点上加入了旋转不变性与尺度不变性；尺度不变特征变换（Scale-Invariant FeatureTransform，SIFT）[7]算法能对旋转、尺度缩放、亮度变化等保持不变性，是一种非常稳定的局部特征优化算法；加速稳健特征（Speed-Up Robust Feature，SURF）[8]算法对SIFT 算法进行了改进，提升了算法的执行效率，为算法在实时计算机视觉系统中的应用提供了可能。

除了对特征点选取进行优化外，还可以对特征点匹配算法进行优化，其中应用最广泛的就是随机抽样一致（RandomSampleConsensus，RANSAC）[9]算法。该算法是一种为了消除误匹配的鲁棒估计方法，对噪声具有较强的鲁棒性和稳定性。在RANSAC算法中，消除误匹配和保持正确匹配取决于阈值。如果阈值偏低，除了消除误匹配之外，还会删除大量的正确匹配；如果阈值偏高，除了保持正确的匹配之外，同时也会保留大量的误匹配，从而降低匹配精度。如果误匹配过多，RANSAC 算法就有可能会失效，从而估算不出较为精确的模型；而当特征点提取过多时，RANSAC 算法的多次迭代也会成为延长算法处理时间的一个重要因素。

为了将RANSAC 算法更好地在不同场景下进行应用，近几年不少学者进行了深入的研究。文献[10]提出了一种考虑空间一致性的内点判断方法（Graph-CutRANSAC，GC-RANSAC），并结合图割算法解决内点判断的优化问题，从而提升了RANSCA 算法的精度与效率。文献[11]提出了PASAC 算法，利用先验信息进行模型估算。该算法分析了视觉里程计特征点跟踪的误差规律，进行了快速的模型生成和不好模型的快速淘汰，使得位姿估计步骤比传统RANSAC 算法更加快速和精确；文献[12]提出了NG-RANSAC（ Neural-Guided RANSAC） 算 法， 将RANSAC 与神经网络相结合。该神经网络可以预测每个观测值的权重，而权重则可以指导最小集的采样，更好地处理误差比例较大的数据。

本文对RANSAC 算法的耗时与精确度进行了优化，其中部分思路借鉴了基于网格的运动估计（Grid-based Motion Statistics，GMS）[13]理 论，并 对RANSAC 算法的随机采样进行了优化。首先对两幅图的特征点进行暴力匹配（Brute-Force)[11]，并按照特征点的匹配质量进行排序；然后借鉴GMS 理论，进一步剔除误匹配；同时利用网格法降低算法的复杂度，对分值最高（网格内特征点匹配正确率最高且匹配对数最多）的3 块网格采用顺序选取策略分别进行模型估算；最后将这3 个模型进行聚合从而获取更为精确的匹配结果。

1 特征匹配算法

1.1 GMS 算法

GMS 算法是一种基于网格的运动统计方法，其目的是为特征点匹配提供一种比较快速且鲁棒的解决方案。主要思想是：实际情况下的物体运动一般都是平滑的，因此假设那些在图像坐标系上相邻的像素往往是一起运动的[14]。

在实际生活中，刚性物体的运动具有一定的一致性，因此相邻像素有很大的概率分布在该物体上。如运动统计示意图（图1）中所示，黄圈内的点都是匹配正确的特征点；绿色连接线的一对特征点在其邻域内有着其他多对匹配的支持（如白线所示）；而红色圈内匹配的特征点其实是错误的，所以该匹配周围就没有能够支持它的其他匹配。

图1 运动统计示意图Fig.1 Demonstrationofmotionstatistics

设有两幅图像 G1和 G2，对这两张图片分别进行特征点提取，并假设经过暴力匹配后一共有n对是特征点匹配，C表示总的匹配集合，ci表示其中的每一对匹配，即C={c1,c2,···,cn}。

正确的匹配受运动平滑性约束，而错误的匹配往往不受其影响。如图1 所示，在邻域内，正确的匹配往往比错误的匹配有着更多的支持，这个支持称为“相似匹配”（图1 中黄色圈内的白色连接线所连接的匹配对），用si表示。所以，“相似匹配”的数量（记作 |S）i| 可以判断某个匹配是正确还是错误，即|Si|可以作为ci运动上的支持。

若对每个特征匹配都进行打分会导致算法的时间消耗过大，时间复杂度达到O(N)（N为特征匹配数量）。所以GMS 算法进一步提出了网格统计的方法，将一幅图像默认划分为20×20 的网格，对每个网格进行评分。

图2 所示的网格框架中，将两个图像G1和G2分别划分为无重叠的网格单元。定义ci是落在单元格Ga和Gb中的匹配（例如图中的红色对应关系）。ci邻域内的特征点被重新定义为

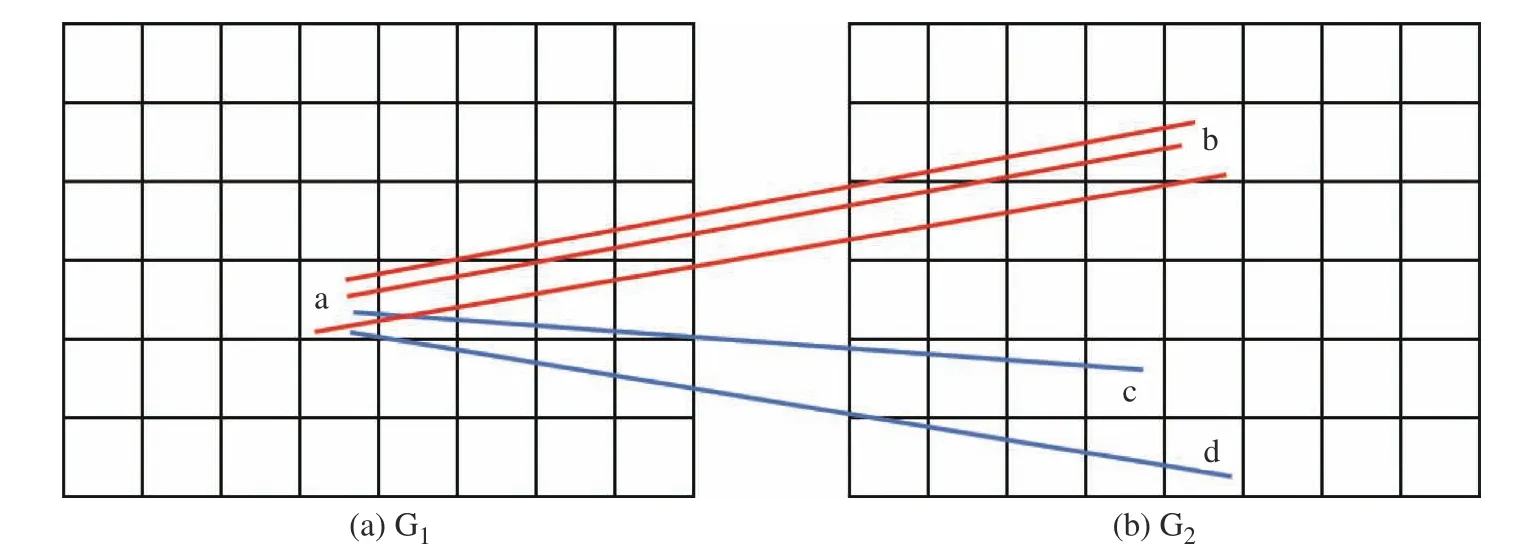
图2 网格框架Fig.2 Grid-basedframework

并且“相似匹配”重新定义为

其中：Ca为位于网格Ga的匹配；Cab为同时落在Ga和Gb上的匹配。也就是说，同一个网格内的匹配都称为“邻居”，用Ni表示；同时在一对网格对内的匹配称为“相似匹配”，用Si表示。落在同一网格单元对中的对应关系共享相同的运动支持，因此只需要对网格单元对进行分类，而不是将所有匹配分别进行正确性区分，从而可以将总的复杂度降到O(1)。

1.2 基于网格运动统计与RANSAC 的优化图像匹配算法

传统的RANSAC 算法先选取少量的几组数据估算出一个模型，然后使用其余的数据对该模型进行验证，统计内点的数量。如此反复迭代一定的次数，选出内点数最多的那个模型作为最终的结果。

将RANSAC 算法应用到视觉中的最终模型是单应性矩阵[15]。单应性矩阵定义了两幅图像之间的映射关系，也就是说，在知道了某点在一幅图像的像素点位置后，可以通过单应性矩阵求得其在另一幅图像中点的确切位置。如式（3）所示：

其中： [x′y′1]T和 [x y1]T分别为3D 空间点在两个像素平面的2D 齐次坐标，这两个像素点通过单应性矩阵（式中3×3 矩阵）建立起对应关系。实际处理时一般令单应性矩阵中的h33为1，因此只有8 个未知参数。即需要随机选取4 对特征点匹配（每幅图中选取的4 个特征点不可共线），列出8 个线性方程进行计算。具体流程如下：

（1）对两幅图像进行特征点的选取，利用暴力匹配方法进行特征点的初始匹配。

（2）随机选取4 对特征点匹配进行估算，得出模型H（单应性）矩阵。

（3）将其他匹配代入模型进行验证，统计内点个数（如果某匹配的误差在一定的阈值范围内则被称为内点）。

（4）迭代到一定次数后，选出内点数最多的模型作为最优解。

从上述步骤中可以看出，传统RANSAC 算法存在较多的局限性，主要分为效率与精度两个部分。首先，特征点的质量与数量对算法的最终结果影响较大，若特征点误匹配较多，则需要进行更多次数的迭代，并且每一次迭代计算得到的单应性矩阵都会对所有的特征匹配进行内外点检验，这大大增加了RANSAC 算法的耗时；其次是RANSAC 算法最终只采用一组解，剩余模型中包含的有效信息全部被舍弃，而这些被舍弃的模型经过算法处理能够提供更多的有效信息，使得位姿估计结果更加精准。

针对这些问题，本文提出了RANSAC 改进算法，算法步骤如下：

（1）首先利用同一物体在相似图像上呈现出的特征点的邻域灰度值往往有较高相似度的特性，对误匹配进行初步筛除。因为RANSAC 算法一般会应用于图像拼接、视觉里程计或是三维重建中，在这些应用场景下，相邻近的图像帧之间的构图和灰度值差异都不会很大。根据这一特性将初始匹配点按照灰度梯度变化的相似性从大到小依次排序，并保留前80%的特征点匹配对作为求参点集UF，从而减少单应性矩阵估计的迭代次数。本文采用8 邻域的拉普拉斯算子[16]（如图3 所示）计算特征点周围灰度值的梯度变化。具体公式如下：

图3 8邻域拉普拉斯算子模板Fig.3 Eight-neighborhoodLaplaceoperator

其中： ∇f(x,表y) 示点 (x,y的) 梯度变化；I(x,y)表示点 (x,y)处的灰度值。

（2）利用GMS 算法对上一步求得的UF内的特征点匹配进行处理，筛除更多干扰，为RANSAC 算法提供更高质量的匹配，从而进一步降低RANSAC 算法的迭代次数并获取更精确的模型。同时利用网格统计方法，分别对得分最高的3 个网格内的特征点匹配进行单应性矩阵的计算，求出每个网格的最终模型。

如图4 所示，A、B 和C 分别为特征匹配得分最高的3 个网格。以A 网格为例，将其邻域（周围红色斜纹部分）纳入计算范围，增加更多的有效信息。将该九宫格区域内的特征匹配作为局部的求参点集，利用RANSAC 算法求解出其对应的单应性矩阵。B 和C 网格的操作与A 一致，分别得到B 与C 的单应性矩阵。

图4 求解高分网格的单应性矩阵Fig.4 Solvethehomographymatrixofahigh-resolutiongrid

将这3 个模型进行聚合优化，进一步提升RANSAC算法的精度，如图5 所示。RANSAC 需要找到一个能满足最多特征点匹配的模型，并让模型估计出的特征点与真实特征点之间的误差尽可能最小（Image2中的红色点是真实特征点，黄色点则是由不同的迭代模型估算出的特征点位置）。可以明显看出，蓝色虚线框内的黄色点距离真实特征点的距离均很近，即模型H1、H2和H3都是较优秀的模型。模型的精确性会受到许多因素的干扰，其中最主要的因素就是其本身的估计噪声以及数据测量的噪声影响[17]。由于较好的候选模型所估算出的特征点位置在真实值附近一般都是呈现零均值高斯分布，所以通过对模型进行聚合，可以尽量消除噪声影响，从而生成更为精确的结果。

图5 模型聚合示意图Fig.5 Demonstrationofmodelaggregation

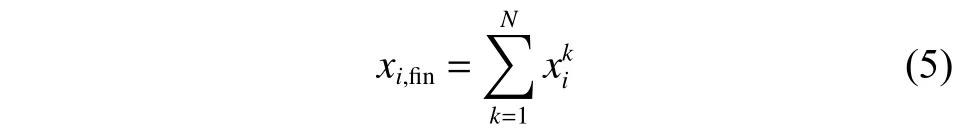
（3）传统RANSAC 算法在求解单应性矩阵的迭代过程中，首先会统计该矩阵对应的内点数目，并将其和设定的期望值比较，若大于期望值，则判定该单应性矩阵为最终模型；反之迭代次数加1，并重复上述步骤，直至达到迭代次数后，选取内点率最高的模型作为最终模型。而随机采样方法有较大的概率选取到质量较差的特征点匹配，导致计算出的单应性矩阵的内点数小于设定好的期望值，从而使得每次计算都需要执行完所有的迭代次数。这种情形不但大幅增加了算法耗时，同时也有较大概率无法获取符合预期的模型。

改进算法步骤（1）中已经对原始的特征点匹配进行了筛选并排序，因此本文对随机采样这一步骤进行优化，变更为按照灰度相似度排序，并依次选取4 组特征点匹配进行计算。

如图6 所示，选取的九宫格区域内的特征匹配已经在步骤（1）中按照灰度梯度变化的相似性从大到小依次排序，所以按照顺序选取4 组特征匹配进行模型计算，这样可以大概率在迭代上限之前求得满足预期要求的高质量模型，从而有效地减少RANSAC算法的迭代次数，提高模型求取的速度。

图6 顺序选取示意图Fig.6 Schematicdiagramofsequentialselection

优化算法的伪代码如下：

（1）Input：N对特征点匹配对

（2）Output：最优单应性矩阵

（3）①对特征匹配进行灰度值相似度排序

（4）对特征点进行BF 匹配

（5）使用式（2）～式（4）进行灰度值相似度排序

（6）取前80%的特征匹配组成求参点集UF

（7）②选取评分前三的网格（以UF替代原始特征匹配集合进行处理）

（8）将图片划分为K个网格，进行GMS 打分

（9）选取评分最高的3 个网格块

（10）分别存储3 对网格块内的特征点匹配M1、M2、M3

（11）③求出模型

（12）for（1≤i≤3）分别对M1、M2、M3进行模型估计

（13） while（n≤迭代次数）do

（14）Mi内进行RANSAC（顺序选取策略）计算

（15） 记录Mi内的最优模型Hi

（16）end

（17）④对3 组模型进行聚合

（18）将3 组模型H1、H2、H3进行特征点聚合

（19）保存并输出聚合后的结果

2 仿真实验

仿真实验使用平台的处理器为inteli7-8750H，内存16GB，运行Ubuntu16.04 系统。用于实验的图像来自牛津大学提供的数据集。为了验证算法的性能，在数据集中选取若干个图片组，每组包含一张参照图像和5 张对比图像。相比于参照图像，对比图像会进行不同形式的变换。如图7 所示，第1 组(图7(a))为模糊变换，即对同一图像用不同的高斯核进行模糊处理，模糊处理后的图像逐一与原始图像进行匹配。其中上方为参照图像，下方为对比图像（一组内共有不同变换程度的5 张对比图像）；第2 组(图7(b))为亮度变换，即对同一图像逐渐降低亮度，将改变亮度后的图像逐一与原始图像进行匹配；第3 组(图7(c))为旋转缩放变换，即对参照图像进行一定程度的缩放并同时逐步增加旋转角度，将变换后的图像依次与原始图像进行匹配。

图7 数据集示意图Fig.7 Demonstrationofdataset

将改进算法分别与经典RANSAC 算法以及GMS 与RANSAC 的融合算法进行对比。所有图像都使用ORB 特征点法进行特征点提取，提取个数为每幅图像2000 个。选取的判定指标为精确率（P）与召回率（R），并且认为与真实的距离小于等于10 个像素的匹配关系是正确的，其余则判定为错误匹配。

其中：NT为算法提取出的正确的特征点匹配数目；N为算法提取出的所有的特征点匹配数目；M为利用数据集给出的单应性矩阵算出的所有的匹配对，即样本中所有的信息总数。

图8～图10 示出了各组图片特征匹配精确率与召回率的折线图，其中横坐标表示每组图像内5 张经过变换的图片。可以明显看到，改进算法在各个场景下都有良好的鲁棒性，性能较传统RANSAC 算法有明显的提升，相比于性能较优的RANSAC+GMS融合算法，精确率提升了4.8%；召回率则提升了6.2%。

图8 不同模糊程度图像结果对比图Fig.8 Comparisonofimagineresultswithdifferentblurvariation

图10 旋转+缩放图像结果对比图Fig.10 Comparisonofimagineresultswithdifferentrotationandscaling

为了检验改进算法对不同特征点的兼容性能，加入了SIFT 特征点的匹配实验。实验所用的数据集与上述一致，具体数据对比如表1 所示。

表1 SIFT 特征点仿真实验结果Table1 SimulationexperimentresultsofSIFT

除了对精确率与召回率的提升，改进算法也采用了与特征点匹配的顺序选取策略以及网格加速方法对算法效率进行优化。为了验证算法的实际耗时，依次增加图像ORB 特征点的选取个数，进行算法耗时测试，结果如表2 所示。

表2 算法耗时对比Table2 Comparisonofalgorithmtimeconsumption

图9 不同亮度图像结果对比图Fig.9 Comparisonofimagineresultswithdifferentluminancevariation

可以明显看出，本文的改进算法相比于传统RANSAC 算法在时间消耗上明显缩短。为了与上文的实验保持一致，将特征点个数为2000 的这组数据进行比较。由表中数据可得，此时RANSAC 算法、GMS+RANSAC 融合算法耗时以及本文改进算法耗时分别为115.80、70.80、78.23ms。对比可得改进算法的计算时间较RANSAC 算法减少32.44%，与GMS+RANSAC 融合算法耗时基本一致，可以更快速地完成较高质量的特征点匹配。

3 结 论

本文在图像特征点匹配算法（RANSAC）的基础上进行了精度与效率上的改进：在使用BF 法初步匹配后，将初始匹配点按照灰度梯度变化的相似性从大到小依次排序；在此基础上对所有匹配进行网格划分并对各网格进行评分，使用顺序选取策略进行模型迭代。最终使用聚合后的最优模型对初始匹配进行筛选，从而获得更好的匹配质量与更少的迭代次数，提升了算法的性能。

仿真实验结果表明，本文提出的基于网格加速与顺序选取策略的优化图像匹配算法在模糊场景、旋转缩放以及明暗变化等不同场景下都具有较好的鲁棒性。相较于一些传统的算法，其精确率与召回率有明显提升；同时，计算耗时较传统RANSAC算法也大幅减少。