巧用“三环四法” 擦亮思维火花——图示法在问题解决中的应用探究

文|戴寅娜

“三环四法”中，“三环”即课堂教学实施的三个环节，分别是：课前借图，自主探索；课中用图，有效学习；课后用图，巩固落实。“四法”是指问题解决的四种策略方法，即选择图示——借助图示——辨析图示——优化图示四种方法。

一、“三环四法”——图示法教学的应用策略

“三环四法”图示解决问题的教学策略。

“三环四法”不仅是一种教学方式的创新，它更是一种观念的更新，一种提升问题解决能力的策略。该策略符合学生的学习认知规律，可极大限度地发展学生的思维能力，提高学生解决问题的能力。

（一）图示法教学的“三环”运用方式

教师只有充分掌握和了解学情，知道学生需求，进而有针对性地教学，才能高效实施课堂教学，落实教学目标，突破教学难点。图示教学的“三环”模式。

正所谓“以其所知，喻其不知，使其知之”。有效运用“三环”图示教学模式，能帮助学生理解较难的数学问题，理清知识脉络，有效帮助学生梳理数学知识的内涵和外延，有助于学生对知识的理解、记忆、巩固和提取，形成主动迁移，搭建知识体系。

1.课前用图，了解学情，精准教学。

课前利用图示进行前测，了解学生知识储备，便于教师在教学中更加精准制定教学目标，为突破本节课的教学难点提前做好预设，为学生的学习提供更高质量的课堂教学。

案例：人教版五年级上册《数学广角——植树问题》例1 教学设计。

（1）《前测单》：

（2）测试结果及分析。

从测试结果看，只有三分之一学生对于植树问题的两端都种这一类问题掌握较好，但是在访谈中发现他们提前在培训班进行了学习，而对于本课重点三类模型思想的建立几乎没有，对于植树问题中的棵树与间隔数的概念也是模糊不清，只是记住了这一类问题的解题方法。所以，教师在教学中应重点对植树规律展开教学，让学生在自主探索中摸索规律，从而建立植树问题的三类模型思想。

2.课中用图，突破教学难点。

图是一种静态的结果，画是一种动态的过程，图示法教学的运用过程就是学生思维方式发生变化的过程。教师教学时善用图示法教学，利用小学生想象力丰富这一特点，鼓励学生运用图示法解决问题，尝试用不同图示展示自己对问题思考的方法，利用图示对所学知识进行梳理，让学生在画图的过程中体验图示的价值，感受学习的乐趣，激发学习潜能。

教学环节一：还原生活，渗透原理

问题：在一条长20 米的小路一旁，每隔5 米种一棵树，你会种吗？

（学生上黑板画一画，画了5 棵树）

师：你们同意吗？

生：同意，因为从这条路的这一端种了一棵树，到最后那一端也种了一棵树，一共种了5 棵树。

师：谁听明白了，再上来给同学们边指边说。

生：把这条路平均分成4 段，每个端点上种一棵树，从头开始种，一共种5 棵树。

师：是呀，我们发现树是种在每个端点上的，求一共种了几棵树就是求一共有几个端点。

师：把每一段左边种一棵树，发现最后多了一棵树，这里的每一段我们把它称为间隔数，一个间隔对应一棵树，发现数的棵数比间隔数多“1”，所以树的棵数＝间隔数+1，这是两端都种的植树问题。

师：像这样把树种在点上，生活中还有很多现象也是把它放在点上的，你能举例说一说吗？

生：路边安装电线杆、走楼梯、节日时挂彩旗……

有了图示的帮助，学生都能建立植树问题的模型，不再只是记住解题方法，能准确应用模型思想解决这一类问题，同时也为后面学习其他两种植树情况埋好伏笔。

3.课后用图，复习巩固。

图示并非只能解决数学问题，课后有效运用图示法进行复习巩固，对培养学生的学习兴趣，提高学习能力都起到了重大作用。四宫漫画、绘本创作等策略都是图示法解决问题后的延伸。

在学习完《植树问题》中三种模型思想后，课后布置一个作业让学生用图示法整理归纳本单元内容，然后教师在学生原有的基础上不断完善总结，学生就会串联知识点之间的关系。

图示法具有直观、形象和有效的特点，不仅是课堂上教师教学的重要手段，更是帮助学生整理归纳分散知识点，提高课堂教学效果的有效方法。图示法在解决问题教学中，无论是教师还是学生都易于上手，对于解决问题能起到高屋建瓴之作用。

（二）图示解题的“四法”应对策略

1.选择图示，感悟价值。

数学是一门抽象的学科，总给人一种难以理解的神秘感。图示法的有效运用，能不断激发学生数学学习的兴趣。只有有了浓厚的兴趣，他们才能全身心投入到数学学习中。

例题：甲乙两队共修一条公路，甲队修了600 米，正好是全长的，乙队修了全长的，乙队修了多少米？

画线段图理解题意（图略）。

列式计算：

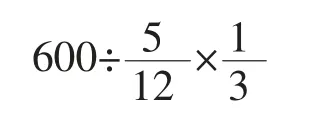
答：乙队修了480 米。

分数应用题较为抽象，学生对于单位“1”概念模糊，分不清具体量和比较量，即使找到了具体量也很难找到对应的分率。事实上，线段图是解决分数问题的有效策略，教师要引导学生正确画图，在线段图中呈现有价值的信息。

2.借助图示，梳理关系。

当学生遇到稍复杂的数学问题时，就会产生借助图示梳理数量关系的需求，说明学生已经形成了画图意识。当学生在解题过程中，有时会解题却不能准确表达题中的数量关系时，需要依靠教师循序指导，引导学生借助图示分析它们的关系，并引导学生思考：先求什么，再求什么？

例题：将一根长3 米，底面直径为2 米的圆柱形木料锯成3 段，表面积增加了多少平方米？这根木料的体积是多少立方米？

此题要想求出“表面积增加了多少？”需要知道：（1）一共增加了几个面？（2）每个面是什么形状？（3）圆的面积怎么求？要解决以上问题，就要在题中寻找信息：（1）一共增加了4 个面。（2）4 个一样的圆。（3）圆面积的计算公式S＝πr2，r＝d÷2。

应用思维导图，清楚地呈现了解决这道题的思路，非常清晰地厘清了所求问题对应的数学信息。如果学生用其他不同图示分析题意，教师都应予以肯定，只要学生有意识用图示理清数量关系，找到解决问题的思路，形成问题解决的策略即可。

3.辨析图示，理解内涵。

当学生能够自主用图示法解决数学问题，准确展示思考过程时，教师还要引导学生会辨析不同图示的内涵。

例题：鸡、兔同笼，共有8 个头，26 只脚。鸡和兔各有几只？

由于学生原有认知水平差异较大，面对学习能力较高的学生，引导其画出更为简单有效的图示。对于画图能力相对弱的学生，具体要求可以适当放低些，鼓励他们亲历体验，了解图示的意义，产生“需要画”的学习体验即可。通过题型教学和题组训练，对其进行针对性的指导，帮助其丰富图示类型，掌握图示方法，从而对图示的理解及其作用的认识逐渐趋向丰满和深刻。

4.优化图示，解决问题。

图示法是解决问题的一种较为有效的策略，但图示法并非解决问题的“万能药”，教师最终应该提升学生的逻辑思维能力，培养核心素养。所以，当学生有意识运用图示解决数学问题后，往往会在脑海中建立模型，不需要再画图理解题意。此时，教师应该鼓励这一类学生在脑海中画图即可。

总之，运用图示法解决问题是提高学生思维水平的有效手段。教师除了自身要善于运用图示法进行教学外，更应注重培养学生主动运用图示法解决问题的意识和能力。