走进“量高”世界

文|程小凤 周 蓉

测量或者估计物体的高度是日常生活中经常遇到的问题之一，如何基于真实问题情境引导学生更好建立高度的感知？本文以学生感兴趣的红色革命基地“七七亭”为项目研究背景，以“如何选用合适工具测量物体高度”为主要研究问题，展开微项目化学习历程，以期丰富学生的体验，发展学生的量感等核心素养。

本项目基于学科核心素养和学科概念，紧扣项目主题和学习目标，设计了《测量“七七亭”》及《校园中的测量》两个子项目。《校园中的测量》又分为测量“校园中教学楼、大树、旗杆、篮球架”四种具有代表性的较高物体展开微项目测量研究，通过选择不同的测量方法测量物体的高度，从而进行归类总结，发展学生的应用意识。首先，带领学生经历头脑风暴，讨论商议量高方法，对比选择测量的学习支架：

一、子项目一：测量“七七亭”

1.实地测量。

结合测量支架，同学们分为几组，选择天气晴好的日子，对“七七亭”进行四种方法的实地测量。

各组测量后发现：

方法一：长木棍组，难以实施。因为找不到木棍和亭子顶端的对齐点。此方法不可行。

方法二：日影、短木棍组，日影难觅。一周连续观察后发现，“七七亭”四周绿植茂密，无论哪个时间段都无法找到影子前端，无法测量出“短木棍”和“七七亭”的影长。此方法也不可行。

方法四：手机APP 组，有局限性。手机中测量APP需在水平位置上测量，当被测物体达到一定高度时，则无法测量，有局限性，测量“七七亭”同样不合适。

方法三：利用等腰直角三角形的性质测量。以自己身体为参照物，找到亭子（除底座外）最低点，在身体上做上标记，然后将等腰直角三角形的一条直角边对准身体的标记点，使得亭子的最低处和等腰直角三角形的水平直角边处于同一平行线上，眼睛和垂直放置的等腰直角三角形在平行处，眼睛从45°角方向找到该点即可量出亭子的高度。

为了数据更精准，小组几人利用三角板多次测量找到最佳位置。各小组基本达成一致，测量出“七七亭”的高度大约是6.9 米。

2.对比改进反思。

6.9米是否准确，与实际高度偏差多大？带着这样的思考，同学们走访了革命前辈，并借助网络和文化馆等资源，查阅了大量资料，在了解革命历史文化的同时，得知“七七亭”的准确高度为6.8 米。在这过程中，同学们也进一步体会到：测量较高物体时，要选择合适的测量工具和方法进行测量才有效，测量过程要尽可能准确，减少误差。

二、子项目二：校园中的测量

校园中也有较高物体，用怎样的测量工具和方法测量合适呢？带着这样的思考，同学们展开了第二次“量高”活动。

1.选择对象和方法。

经过小组讨论决定，选择校园中教学楼、大树、旗杆、篮球架四种具有代表性的较高物体展开测量。

2.分组测量和反思。

教学楼组：借助红外线测距仪、投影比例、等腰直角三角形的性质，都得出结果约为17 米。还发现，原来在设计过程中要考虑到使用功能，所以第一层相对较高。

大树组：选择了老教学楼前枝叶茂密的一棵大树，发现红外线测距仪无法测量。投影比例、等腰直角三角形的性质这两种方法都可行。但在测量中发现选择的大树略有倾斜，导致测量数据不够精准，测量的数据小于大树的实际高度。

篮球架组：篮球架相对较矮，四种方法都可以，用投影比例最方便。还请了体育老师帮忙，借助卷尺和人字梯直接测量。

旗杆组：场地最为宽敞，测量过程也最快速方便，示意图如下：

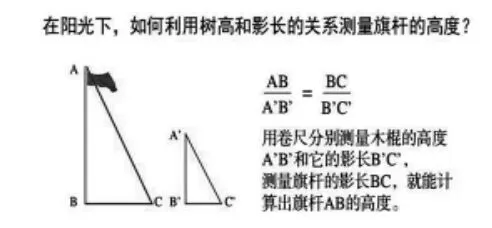
（方法二：投影法）

（方法三：角度法）

3.交流研讨改进。

各小组利用课间时间分别测量实践后，全班在课堂中分享过程，交流研讨。

“量较高物体的高度”可以有不同的方法，每种方法都有优缺点，需要根据测量对象和高度来确定合适的测量工具和方法。

与此同时，各小组也提出了困惑与存在的问题。大树组提出需要选择一棵处在空旷场地上的笔直的大树才能用上述方法尽可能准确测量。篮球架组发现直接测量时卷尺可能出现偏差，难以和地面处于垂直状态，最好准备一根笔直的长木棍固定，测量结果会相对准确。在角度法测量时学生还发现虽然能测出物体高度，但是很不方便，且容易出现较大误差。于是对此方法进行了改进（如下图）。

另外，针对部分学生提出的困惑：如果没有阳光，投影法还适用吗？各组进行了思考和讨论，产生了以下方案（如下图）。

为了验证上述两种方法是否适用，各组选择了阴天再次尝试测量，并结合实际，对适合的其他方法进行了改进实施。

三、项目评价

在整个项目实施过程中，结合项目主题和项目学习目标，我们制定了各类评价量表，并即时展开过程性和结果性评价。下表为过程性评价量表：