两轮车事故影响因素分析及损伤机理研究*

2022-10-25王仲旭陈泽平鲁誉刘强解孝民

汽车技术 2022年10期

王仲旭陈泽平,2 鲁誉,3 刘强,3 解孝民

（1.中山大学，广州 510006；2.广东省海洋工程施工与水上应急救援工程技术中心，广州 510006；3.中山大学-广汽研究院智慧交通与人工智能联合实验室，广州 510006；4.广东玛西尔电动科技有限公司，肇庆 523268）

主题词：两轮车安全风险因素逻辑回归事故重构损伤机理

1 前言

2019年，我国发生的道路交通事故中，涉及非机动车（主要为两轮车）的事故占比为11.73%，其中导致骑行人伤亡的最常见事故类型是两轮车-机动车碰撞。作为道路交通中的弱势群体，骑行人在与机动车的碰撞事故中更容易发生致命损伤。因此，研究两轮车-机动车碰撞事故影响因素，探究骑行人损伤机理，对于减少两轮车事故发生具有重要意义。

关于两轮车交通事故严重程度影响因素的研究，国内外学者大多采用离散结果模型将损伤作为名义变量或有序变量，常用的模型是逻辑回归（Logistic Regression，LR）模型和概率单位模型（Probit Model）。徐程、周继彪等分别以杭州和宁波涉及电动自行车的事故数据为基础，建立事故严重程度影响因素逻辑回归模型和概率单位模型，探究了骑行人年龄、性别及驾驶行为等因素对骑行人损伤程度的影响。Robartes、Nenad 等分别使用有序概率单位和逻辑回归模型分析弗吉尼亚2010～2014 年自行车碰撞数据和贝尔格莱德交通学院2001～2010 年期间发生的涉及动力两轮车的交通事故，探究驾驶员、车辆和道路特征对骑行人伤害严重程度的影响。以上研究多通过建立统计学模型对两轮车事故数据进行分析，仅得到了事故严重程度影响因素，并未分析骑行人的具体损伤机理。

关于两轮车事故骑行人损伤机理的研究，有学者利用计算机数学技术，通过事故重构方法进行了分析。马兴会等以车速和碰撞位置为变量，分别建立了汽车-电动两轮车和汽车-自行车有限元碰撞模型，结果表明，反映人体损伤特性的评价指标均与汽车车速呈正相关，与两轮车车速相关性较弱。Huang 等运用MADYMO 建立了两轮车与机动车事故的12 个碰撞场景，结果表明，骑行人头部损伤风险随机动车速度的提高而增加，而两轮车速度及骑行人与机动车相对高度对运动响应具有非线性影响。以上研究多通过事故重构方法研究损伤机理，尚未考虑事故严重程度影响的关键因素。

本文基于广东省涉及两轮车的交通事故数据，建立事故严重程度逻辑回归模型，确定对事故严重程度有显著影响的因素，并设置两轮车-机动车碰撞事故仿真参数，探究这些风险因素对骑行人损伤程度的影响。

2 数据与方法

2.1 数据来源

本文数据来源于广东省交通事故数据库，选取2006～2018 年广东省发生的30 925 起涉及两轮车的事故。每一条事故记录包括人员信息、车辆特征、道路条件、事故发生时间、环境条件和伤害严重程度等信息。为保证分析的准确性，数据记录中的空白和不确定信息均删除。

2.2 变量选取

2.2.1 因变量

为了确定与两轮车事故相关的风险因素，设定事故严重程度为因变量：“1”=财产损失；“2”=受伤；“3”=死亡。

2.2.2 自变量

交通系统由人、车、路和环境等多个因素组成，是一个动态系统，任何一个环节出现问题，都可能导致交通事故。因此，从事故数据中初步选取骑行人、驾驶员属性，以及车辆、道路和环境等因素中的33个变量作为候选自变量，变量赋值如表1所示。

表1 自变量赋值及含义

2.3 研究方法

逻辑回归是研究分类观测值（因变量）与影响因素（自变量）之间关系的一种多变量分析方法，该自变量应为分类变量（两类或多类），当该自变量有2个以上分类时，称为多元逻辑回归模型。本文采用有序多元逻辑回归模型，建立事故严重程度与各因素之间的关系，从而识别出各因素对交通事故严重程度的影响。有序多元逻辑回归可以看作是将因变量分割为多个二元逻辑回归的拟合，在二元逻辑回归模型中，发生严重事故的概率可以表示为：

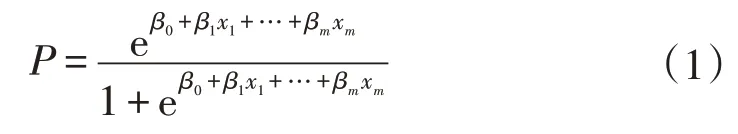
式中，,,...,x为选择的影响因素；为常数项；,,...,β为影响因素,,...,x的回归系数，表示自变量与因变量之间的相关性。

则发生严重事故的概率与不发生严重事故概率的比值可以表示为：

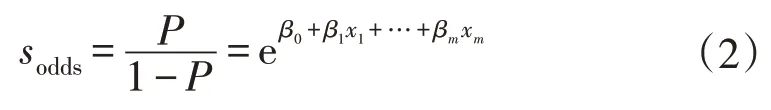
3 分析结果与讨论

采用SPSS软件建立有序多元逻辑回归模型分析两轮车事故严重程度的显著影响因素。参考Kim 等的研究，模型中保留了显著性水平为0.05的自变量，从模型估计结果中，可以筛选出一些对两轮车事故严重程度有显著影响的因素。

3.1 驾驶员与骑行人因素

表2 所示为通过逻辑回归模型筛选出的与驾驶员和骑行人相关的影响因素，以及这些因素的显著性水平及优势比（Odds Ratio，OR）。

表2 逻辑回归模型涉及驾驶员与骑行人因素的估计结果

从表2中可以发现，女性驾驶员和女性骑行人遭受致命伤害的可能性更小，表明男性驾驶员和男性骑行人在两轮车事故中可能面临更大的碰撞风险。总体而言，女性比男性更谨慎，攻击性更弱，因此发生致命事故的风险更低。此外，驾龄也是重要因素，以＞10 年为参考类别，表2 揭示了驾龄为7～10 年的驾驶员发生致命事故的概率更高，对应的优势比结果表明，其发生致命事故的概率比拥有10年以上驾龄的驾驶员高15.4%。

3.2 车辆因素

逻辑回归模型关于车辆因素的估计结果如表3 所示，可见车辆类型、行驶状态、车辆安全状态和事故形态是影响两轮车事故的重要因素。

表3 逻辑回归模型涉及车辆因素的估计结果

表3 结果表明：以小汽车为参考类别，本研究选择的3 种车辆类型都有可能造成致命损伤。其中大货车的损伤概率最高，是小汽车的4.104倍，这可能是由于大货车具有更大的惯性。其次是大客车，发生致命事故的概率是小汽车的2.316 倍。此外，正面碰撞造成致命损伤的概率更高，目前考虑事故形态对事故严重程度影响的研究较少，尤其是涉及两轮车的交通事故。本文采用事故重构的方法，进一步分析追尾、正面碰撞和侧面碰撞3 种碰撞形式下不同碰撞角度对骑行人损伤的影响。

3.3 道路因素

表4 列出了与道路相关的影响因素及其显著性水平和优势比。由表4 可知，在道路横断面位置、交通信号、路侧防护措施、路表状况和道路线形等因素对事故严重程度有显著影响。

表4 逻辑回归模型涉及道路因素的估计结果

根据表4结果，机动车道比非机动车道更容易发生致命损伤。两轮车骑行者有时会违反交通规则在机动车道行驶，如果与机动车发生碰撞，由于道路上的车辆速度相对较高，骑行人发生损伤的概率更高。道路上的一些交通设施（交通信号和路侧防护设施）对降低骑行人的伤害程度有一定作用。乱穿马路的情况在国内较常见，尤其是在没有交通信号的情况下，驾驶员撞到骑行人的概率会更高，表4 显示，交通信号可使致命事故概率降低34%。此外，在干燥路面发生致命损伤概率比其他路面高66.5%，这可能是由于驾驶员在干燥路面行驶时容易放松警惕，行驶速度过快。

3.4 环境因素

环境因素的显著性水平与优势比如表5 所示：星期、季节、时段、天气、能见度和照明情况与两轮车事故相关。

表5 逻辑回归模型涉及环境因素的估计结果

由表5可以看出，两轮车在无照明夜间发生致命损伤的概率是白天高峰时段的1.611 倍，可能是由于驾驶员在夜间行驶时视线受到了很大的限制。然而，当道路周围有路灯时，致命损伤的概率降低了27.9%。以雨雪天气为对照组，阴天因素下的优势比为1.174，这意味着在阴天发生致命损伤的概率是雨雪天气下发生致命损伤的概率的1.174 倍。能见度也会轻微影响骑行人发生损伤的概率，由表5可见，能见度小于50 m时，发生致命损伤的概率最高。这可能是由于此时警察执法力度较弱，驾驶员鲁莽行为较多且认为违法被处罚的可能性较低。

4 事故重构

本文采用事故重构的方法进一步分析逻辑回归模型得到的显著影响因素导致骑行人发生损伤的机理。

4.1 重构模型

如图1 所示，基于MADYMO 仿真软件，建立两轮车-小汽车的碰撞模型。图1a中，选取4种不同碰撞角度（0°、60°、90°、120°）表示发生的3种不同事故形态（追尾、正面碰撞和侧面碰撞）。根据现有的事故数据，选取3种不同的路表状况，即干燥、积水以及其他状况，其对应的地面摩擦因数分别为0.7、0.5 和0.3。假人模型、两轮车以及小汽车的多刚体模型如图1b 所示。采用MADYMO 中第50百分位男性假人模型作为参考假人，该模型此前已通过人体解剖试验的结果进行验证，并被有效地用于车辆-自行车的事故重构研究。

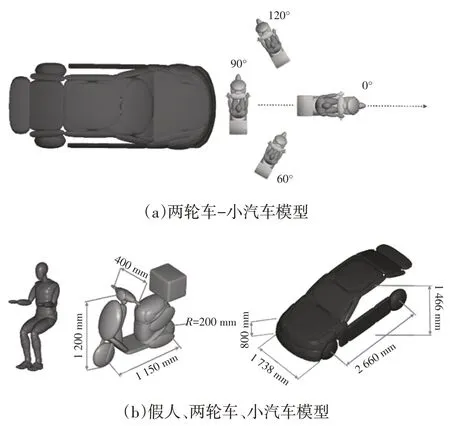
图1 重构模型的相应尺寸

在模型验证过程中，当两轮车与小汽车的速度分别设为15 km/h和40 km/h时，模型中假人与事故视频中骑行人的运动趋势相同（如图2所示）：在与汽车第一次接触后，骑行人的头部转向发动机罩，在空中发生旋转后坠落地面。基于此，验证了模型具有进一步研究的可行性。整个碰撞过程时间设置为1 500 ms，模拟骑行人从开始与机动车接触到坠落到地面的全过程。采用头部损伤标准（Head Injury Criterion，HIC）来评估骑行人头部损伤的严重程度，通过比较整个碰撞过程以及分析对应的HIC结果来确定骑行人的损伤程度：

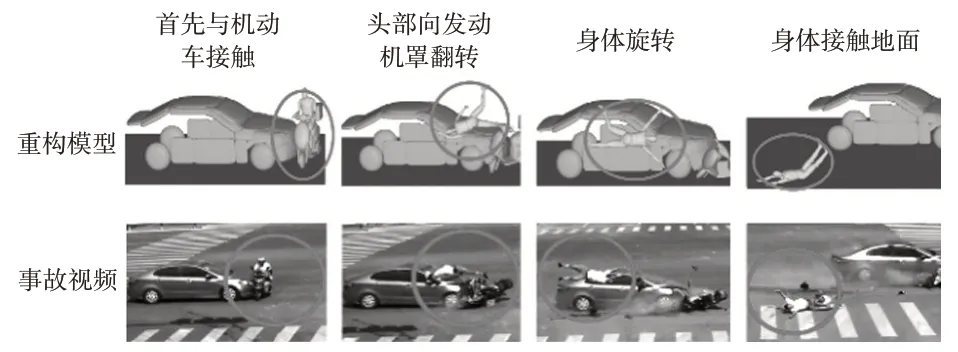
图2 重构模型与真实事故的运动学对比验证

式中，()为头部中心的合成加速度；、分别为HIC 值达到最大值时的起始时刻和结束时刻。

4.2 碰撞角度对头部损伤的影响

图3展示了4种不同碰撞角度下两轮车-小汽车碰撞的运动学过程。

图3 运动学过程

由图3可知，整个运动学过程可以分为3个阶段：当碰撞角度为60°和90°时，在阶段Ⅰ，假人或两轮车首先与小汽车接触，并在阶段Ⅱ开始向发动机罩、前风窗玻璃翻转，在阶段Ⅲ，假人开始沿着前风窗玻璃、发动机罩向下滑动，最终落到地面并停止；当碰撞角度为0°和120°时，与其他2 个碰撞角度不同，两轮车与小汽车接触后，在水平和垂直方向上都发生了较大位移，然后开始失去平衡，最终假人头部着地。

本文根据设定的仿真条件进行了多组试验，通过对试验数据的整理和分析，得到了4种不同碰撞角度对骑行人损伤的影响，如图4所示。设置碰撞时间=1 500 ms模拟整个碰撞过程，设置=300 ms模拟接触的瞬间并记录HIC。从图4a 中可以看出，当碰撞角度为90°时HIC相对较高，说明此碰撞角度对骑行人的冲击较大，这一结果与3.2节逻辑回归模型得到的结论一致：正面碰撞（即碰撞角度为90°）造成致命损伤的概率最高。通过分析图3 两轮车-小汽车碰撞过程，90°的碰撞角度下，发生碰撞后，骑行人头部撞击机动车发动机罩而后发生扭转造成严重损伤。图4b 表明，在接触瞬间，60°的碰撞角度下，骑行人头部损伤值相对较大。分析图3碰撞过程，可能是因为在60°的碰撞角度下，骑行人失去重心后头部撞向前风窗玻璃，短时间内头部受到的冲击力较大，造成严重损伤。

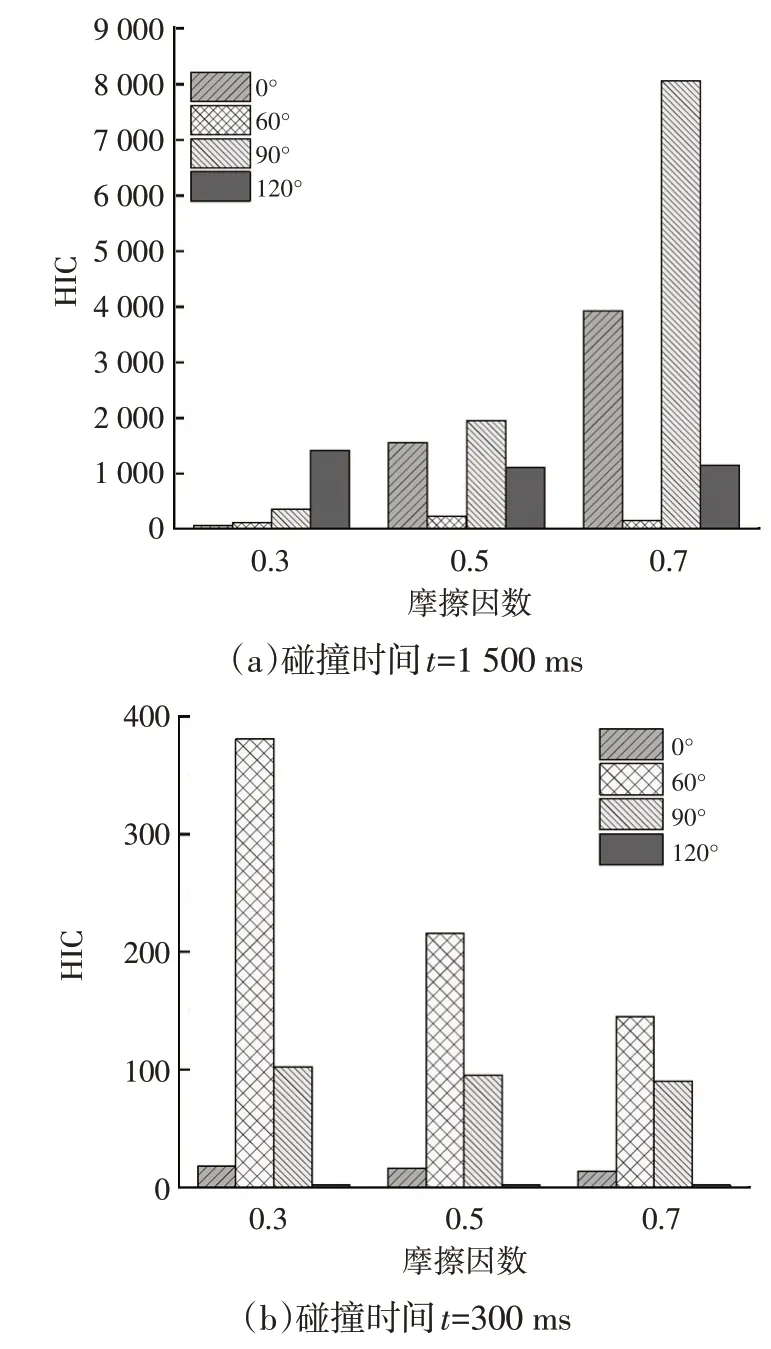
图4 3种不同摩擦因数下不同碰撞角度的HIC

此外，比较2 种类型的侧面碰撞，分析整个碰撞过程，两轮车与小汽车在相反方向（碰撞角度为120°）行驶时比同向（碰撞角度为60°）行驶时更容易发生严重的头部损伤。分析图3 可以发现，在120°碰撞角度下，骑行人倾向于头部直接着地而不接触车辆，因此与60°的碰撞角度相比，120°的碰撞角度下更容易在短时间内对骑行人头部造成严重损伤。

4.3 路面情况对头部损伤的影响

如图4a所示，分析整个碰撞过程，当碰撞角度和速度恒定时，随着路面摩擦因数增加，骑行人头部损伤值相应增加，这表明摩擦因数越大，对骑行人头部造成的损伤越严重。该结果与3.3节逻辑回归模型结论一致：在干燥路面发生致命损伤的概率比其他情况的路面提高66.5%。

图5 对比了不同摩擦因数下发生碰撞后骑行人运动过程的3个阶段。如图5a 所示，当碰撞角度为0°时，不同摩擦因数下骑行人的运动学过程相似，也验证了图4b 中得到的3 种不同摩擦因数下HIC 相差不大的结果。但在干燥路面（摩擦因数=0.7）下，发生碰撞后响应时间较短，受到的损伤也较严重，这可能是由于地面摩擦因数较小（0.3和0.5）时，两轮车由于惯性作用在向前运动一段时间后再发生侧翻，因此在短时间内受到的损伤相对较小。

图5 不同摩擦因数下碰撞过程对比

如图5b 所示，当碰撞角度为90°时，在摩擦因数为0.3 和0.5 的路面上，骑行人发生碰撞后的运动过程相似。比较此碰撞角度下3 种不同摩擦因数路面上骑行人的运动学过程可以发现，骑行人在与小汽车接触后，都是向发动机罩一侧翻转，随后骑行人头部撞击发动机罩，造成严重损伤。图4b 也揭示了此碰撞角度下，3 种不同地面摩擦因数对应的骑行人头部损伤值近似相等。而比较120°的碰撞角度下HIC可以发现，无论设置碰撞时间为300 ms模拟接触瞬间，还是1 500 ms模拟整个碰撞过程，3 种地面摩擦因数对应的HIC 均相差不大，表明此角度发生碰撞时，骑行人头部损伤值与路面状况相关性较小。