计及新能源接入的主动配电网多目标优化仿真

杨嘉静，程若发，许立斌

(南昌航空大学信息工程学院，江西 南昌 330063)

1 引言

随着社会的不断进步，对电能的需求也越来越多。为了满足社会更多的用电需求，电网也在朝着更高效、灵活及可持续的方向不断发展。分布式可再生能源的大力发展也成了必然的趋势。主动配电网是一种具有将分布式电源(DG)、可控负荷、储能、需求侧管理等各种分布式电源组合控制的配电网络，主动配电网能够提高配电网对可再生能源的接纳能力、用户的用电质量以及供电的可靠性。目前对主动配电网的研究较多，也取得了显著的成果。文献[6]是通过网损、投资运行效益等指标，并提出相应算法进行求解，来进行主动配电网的优化配置。文献[7]建立了主动配电网双层规划模型，来确定分布式电源的安装位置和最佳出力。文献[8]是利用联络线投资和供电可靠性确定联络线的位置，再利用DG渗透率和网损确定DG的安装位置和容量。上述文献主要解决分布式电源的安装位置和容量，但都未考虑新能源及其出力问题。

考虑有关新能源出力不确定性的问题，文献[9]利用概率统计对分布风电场发电功率不确定性进行研究，采用基于潮流分析灵敏度的方法对其模型进行求解。但此研究未考虑光伏发电的随机性。文献[10]考虑了风光及负荷的随机性并建立了基于机会约束的双层规划模型。使用分段二进制编码方式和遗传算法对模型进行求解。但其未考虑系统的电压稳定性指数及有功损耗。文献[11]考虑了新能源的加入，但其未分析系统的电压稳定性等指标。文献[12]考虑可再生能源及需求侧资源，提出了微电网双层优化调度模型，基于神经网络对性能指标进行评价。但其重点在于实施改进分时电价后负荷的变化。

文中针对风光及负荷出力的不确定性，构造了一种主动配电网的双层规划模型。其中，上层模型是以系统的网络有功损耗为目标函数，下层模型是根据分布式电源的节点电压稳定性指数、投资效益指标建立多目标优化规划数学模型来确定安装容量；然后，采用改进的差分进化算法对上层模型进行求解，量子粒子群算法对下层模型进行求解。最后将所提模型与已有模型进行比较，证明其优越性，并证明所提模型应用到配电网中能大大提高配电网的安全性和经济性。

2 分布式电源的随机出力模型

2.1 风速概率模型

风电出力的不确定性是由于风速的不断变化导致的。大部分地区的平均风速概率密度分布都服从Weibull分布

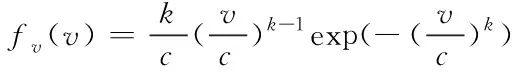
(1)

式中：尺度参数，为实时风速，为形状参数，它能够反映风速分布的特点。不同地区的尺度参数和形状参数是不同的。

风力发电输出功率与实际风速的关系为

(2)

式中：为切入风速，为额定风速，为切出风速，P为风力发电机额定功率。

由于风机输出功率特性受风速的影响。当<或>时，风力发电机不发电，风力发电的有功出力为0；当≤≤时，风力发电的有功出力和风速是线性关系；当≤≤时，风力发电的有功出力为风力发电机的额电功率。由此可得，当≤≤时，风机出力概率密度函数为：

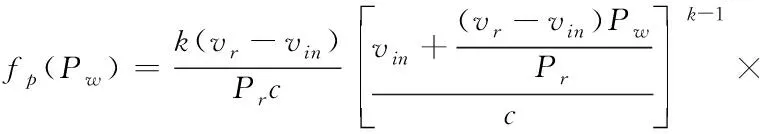
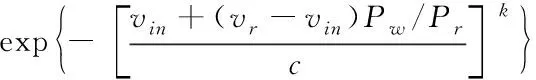
(3)

2.2 光伏概率模型

太阳电池的输出功率与太阳的光照强度密切相关，太阳的光照强度服从Beta分布，其概率密度函数为

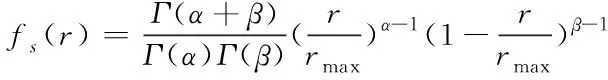
(4)

式中：、为Beta分布的形状参数，Γ为Gamma函数，为最大光强，为光照强度。

光伏发电的有功出力为

=

(5)

为光照面积，为光电转换效率，为光伏最大输出功率。

由上可得，光伏出力的概率分布为

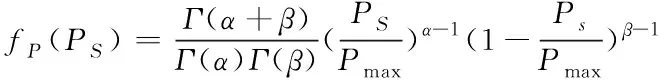
(6)

2.3 基于序列运算的日出力曲线计算模型

在此利用离散化处理光伏出力和风电出力的概率分布。由前两节可得到光伏出力和风电出力的概率分布，将该概率分布离散为概率性序列()和()。分布式电源()的概率性序列的长度为

(7)

概率性序列(＿)为

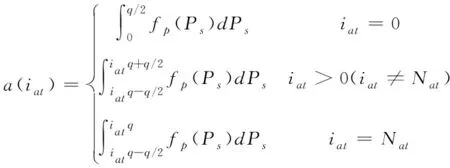
(8)

式中：()是已知的分布式电源发电出力的概率密度函数。

则风光出力的期望为

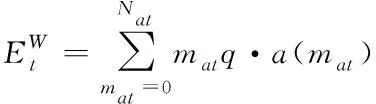
(9)

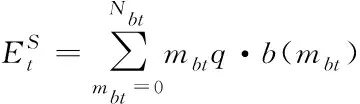
(10)

3 主动配电网双层多目标规划模型

3.1 上层模型

上层模型是根据系统的网络有功损耗来确定的安装位置，网络有功损耗优化指标为

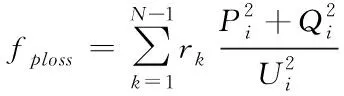
(11)

式中：为网络节点数；为支路的电阻；为支路的首节点号；为节点的电压幅值；、分别为流入节点的有功和无功功率。

文中在考虑电网安全性能更好的前提下优化其经济性能，因此文中在上层模型中，在优化出的最佳接入位置时，先对其电压稳定性指标进行判定，当>009时，选择此次优化的最佳位置；否则，选择此次优化之前的接入位置。然后再使用网络损耗指标对其优化位置进行判定。

3.2 下层模型

下层规划是根据分布式电源的节点电压稳定性指数及分布式电源的投资效益来确定安装容量。

1) 电压稳定性指数

电压稳定性指标一定是小于1的，其值越小说明系统电压越稳定。电压稳定性指标如下

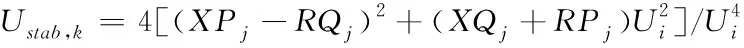
(12)

式中：为支路的电抗；为支路的电阻；、为末节点流入的有功功率和无功功率；为各支路首节点的电压幅值。

2) 分布式电源的投资收益

分布式电源的投资收益为单位分布式电源投资所获得的年收益，即

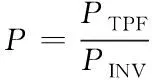
(13)

式中：为投资分布式电源折算到每年的年收益，包括卖出电所得收益和得到的政府补贴。为投资分布式电源折算到每年的投资成本，包括分布式电源的安装成本、运行和维护费用及燃料费用。

3.3 年购电费用计算模型

在模型中，一年被分为四个季节，每个季节取其中有代表性的一个月求取平均值来表征分布式电源的出力情况。首先对风光数据进行整理，一天被分为24个时间间隔，5采样一次，一天采样288次，将每12次的值求取平均值作为一小时的值；然后将30天对应的24小时的值求平均值，得到的24小时的值就是这个季节的代表性小时，这样就有96个小时代表风速和光照强度；最后利用第二节所提方法求取四个季节的风光出力期望值。

年购电费用如下式

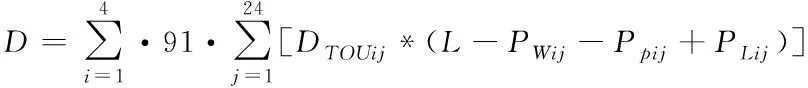
(14)

其中为第个季节第个小时的分时电价；为负荷值；、、分别为第个季节第个小时的风力发电期望出力、光伏发电期望出力及对应网损。

4 主动配电网双层规划的模型求解

文中用改进的差分进化算法求解上层模型，其流程图如图1所示；使用量子粒子群算法来求解下层模型，流程图为图2。

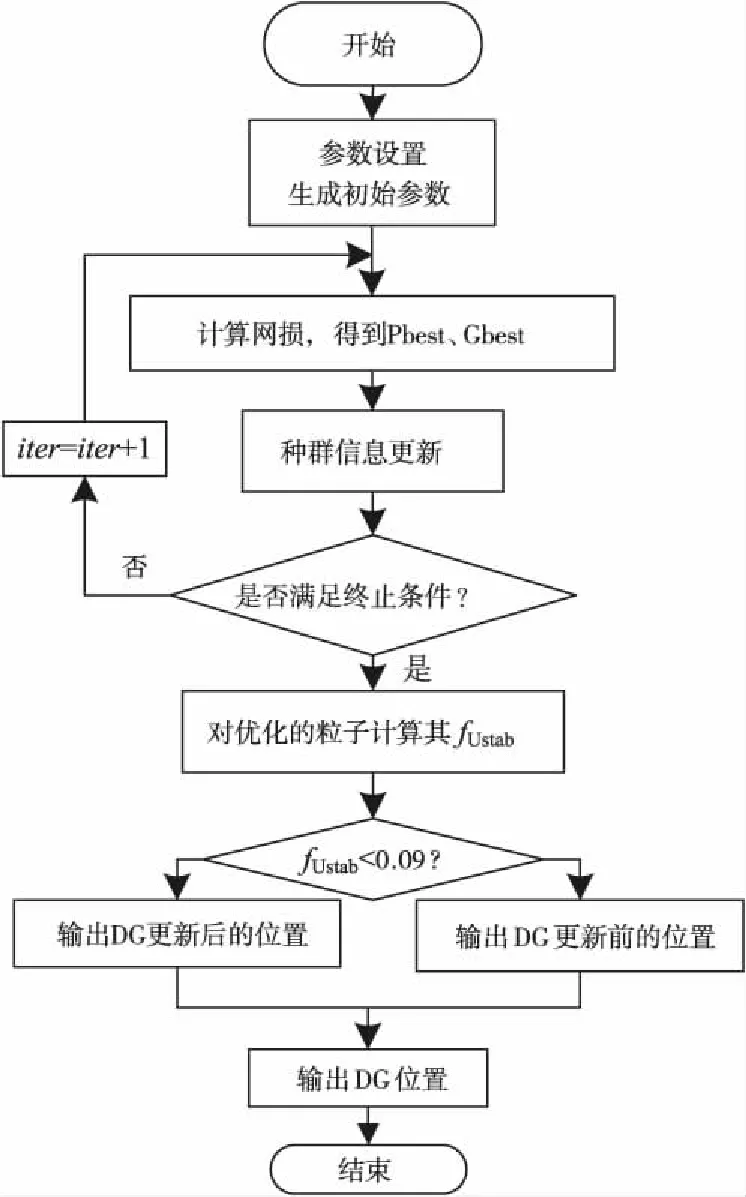
图1 上层规划流程图

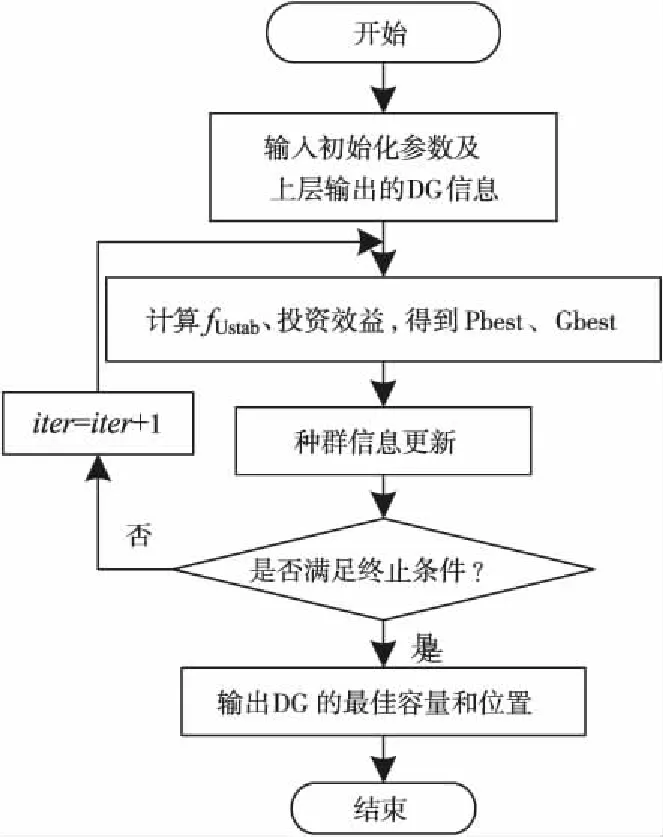
图2 下层规划流程图

4.1 改进的差分进化算法

标准的差分进化算法是从任一随机种群开始，其核心操作主要由：变异操作、交叉操作及选择操作三部分组成。在差分进化算法中，参数缩放因子和交叉概率的变化会很大程度上影响算法的收敛能力和搜索能力，因此文中分别令和服从正态分布和柯西分布

=(，01)

(15)

=(，01)

(16)

、是用来更新和的值

=(1-)*+*()

(17)

=(1-)*+*()

(18)

式中：为常数，()为算术平均值

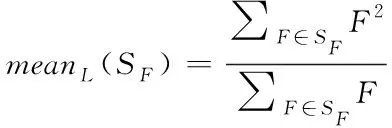
(19)

4.2 量子粒子群算法

量子粒子群是在粒子群算法的基础上基于量子力学对算法进行了改进，增强了算法的全局搜索能力。粒子位置的迭代方程

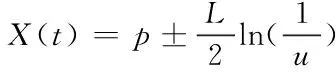
(20)

式中：为随机数；是用来决定粒子个体的搜索范围，表示为

(+1)=2|-()|

(21)

由此可以推导出粒子的进化方程为

(+1)=()±*

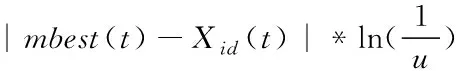
(22)

式中：为当前代数所有粒子的平均最佳位置，其计算式为

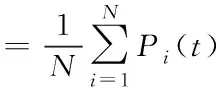
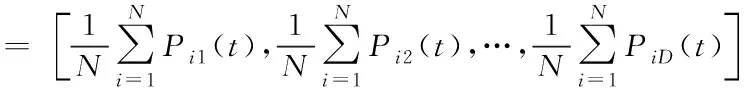
(23)

()为第次迭代时第个粒子的最优位置，其式为：

()=*()+(1-)*()

(24)

式中：为当前迭代次数；()为第维的当前最佳位置；()为第维的全局最佳位置。

5 算例部分

5.1 双层规划模型计算

文中基于MATLAB对IEEE33节点配电系统进行仿真分析，图3为IEEE33节点系统的网络框架图。其中电压等级为12.66 kV，总有功负荷为3715 kW，总无功负荷为2300 kvar，系统线路等参数见参考文献[19]。量子粒子群的算法、改进差分进化算法参数设置如下：种群数量为80，粒子维度为2，最大迭代次数为10。

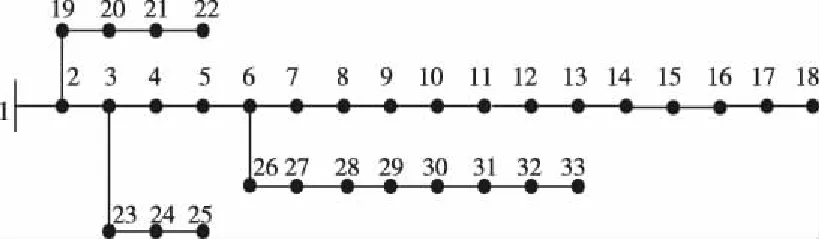
图3 IEEE33节点配电系统

表1为DG投资运行的相关参数，拟安装分布式电源为4个、DG总输出功率不超过网络总负荷的25%，采用文中算法优化得到的DG安装位置与容量如表2所示。14、18、25、32节点分别对应微型燃气轮机、燃料电池、光伏机组、风力发电机组。

表1 DG投资运行相关参数

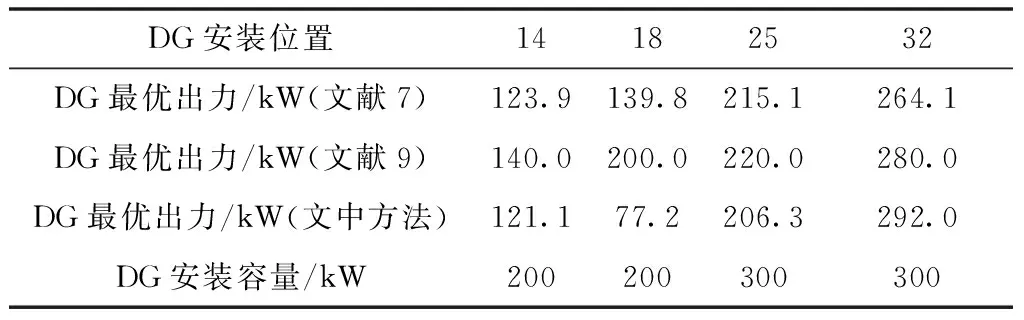
表2 分布式电源的安装位置及出力

图4是规划优化前后及不同算法的优化情况，采用文中优化模型优化后，系统的有功损耗为76.4431 kW，节点最低电压为0.9531，电压稳定性指数为0.0353。与优化前的初始网络相比较，其有功损耗降低了62.28%，节点最低电压提高了4.63%；与文献[6]所用的优化方法相比较，文中优化出的有功损耗降低了43.55%，节点最低电压提高了2.34%；与文献[7]所用的优化方法相比较，文中优化出的有功损耗降低了40.11%，节点最低电压提高了2.14%。

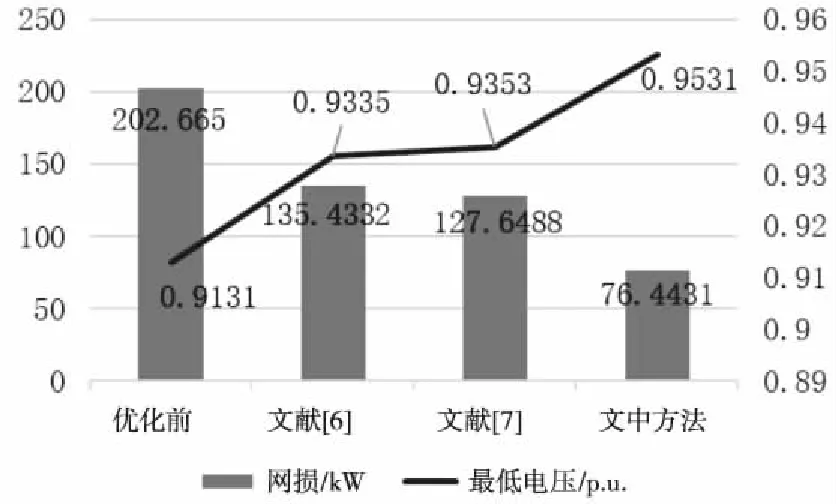
图4 优化对比结果

表3为两种典型的优化规划及文中优化结果的对比。从表中可以得出，文中算法优化出的投资效益为0.5228万元，网损为76.44 kW。相比方案一投资效益增加了27.36%，网损降低了51.21kW；相比方案二投资效益增加了10.59%，网损降低了57.85 kW。

表3 结果对比

图5为不同优化方案下的系统电压幅值，将文中方法与优化前及方案一、二相比，系统的电压水平明显提高。综上所述，文中所提双层规划方法能从多个方面同时进行优化，为决策者提供更为合理的方案。

图5 系统节点电压幅值

5.2 对系统的安全性和经济性分析

文中考虑了风电注入功率及负荷不确定的情况，风电的出力主要受风速和光照强度的影响，不同季节的风速和光照强度相差很大，因此将一年分为四个季节来描述风光出力情况，如图6、7所示。

图6 四季风电机组出力期望

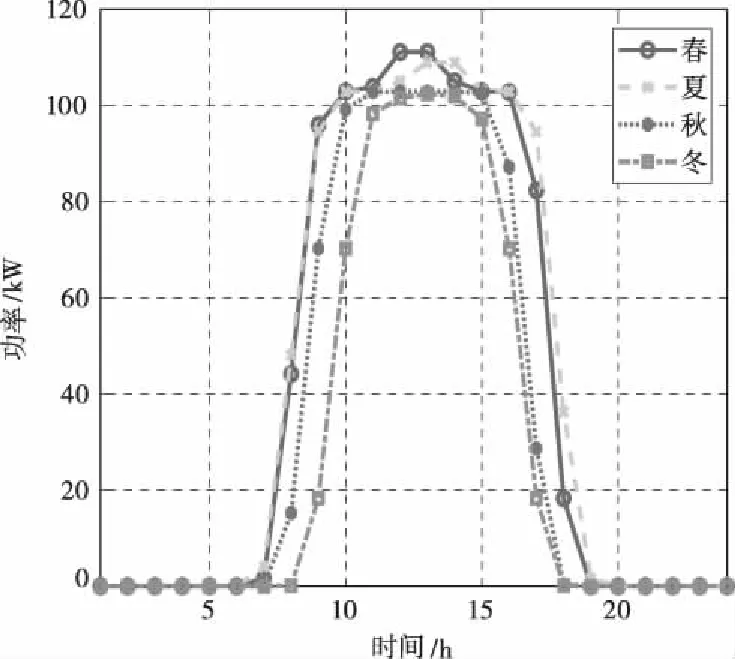
图7 四季光伏机组出力期望

由双层规划得到的分布式电源的安装位置与安装容量。在15节点接入负荷，31节点接入风电机组，16节点接入光伏机组，19节点接入微型燃气轮机。

第一阶段考虑风电接入对电网系统的安全性影响。图8为在15节点接入负荷时，系统接入风光前后15节点电压及网损24小时的变化情况。可以看出在计及风光不确定性的情况下，合理的接入DG可以有效的提高节点电压。特别是在12时到16时风光出力期望值都较高的时刻，电压值提高比较明显，此时段的网损也平均减少了40%左右。

为了进一步验证加入风光的有效性，文中选取时刻12：00，在考虑系统加入负荷的情况下加入风电。图9展示了加入风光之后的配电网的节点电压情况，由图可见加入DG之后，电压优化效果很明显，最低点电压由0.9133

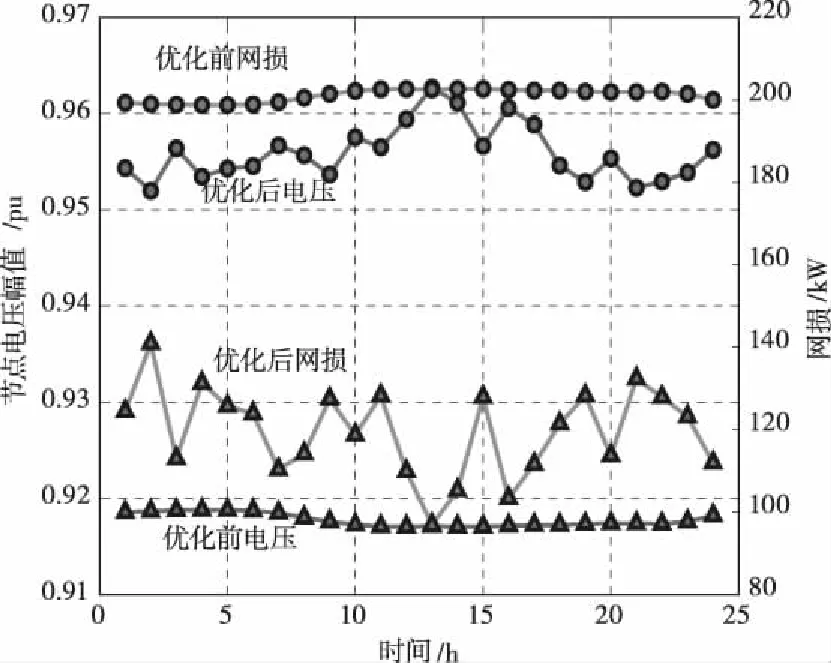
图8 15节点24小时的电压幅值及网损

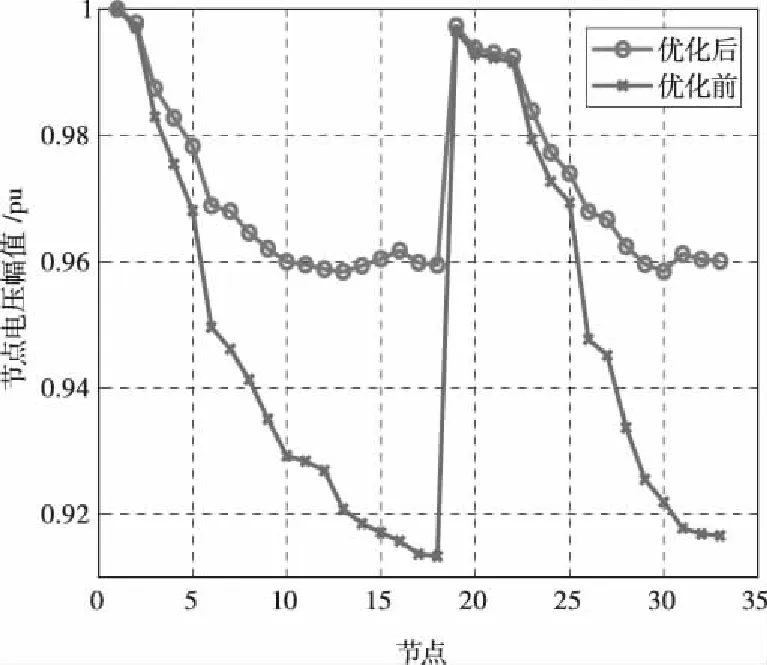
图9 计及风光的电压幅值优化效果

提升到0.9584，提高了4.94%。整体节点的电压提升效果也比较显著。系统网损也由之前的202.65 kW降到117.58 kW，降低了41.97%。

第二阶段对风电接入不同情形下的电网系统基于分时电价的经济性进行分析。分时电价分为三段，其中春夏电价相同，秋冬电价相同，电价情况如图10所示。情形一：不考虑分布式电源的接入；情形二：一个节点接入风力发电机组，一个节点接入光伏发电机组；情形三：只安装风力发电机组；情形四：只安装光伏发电机组。

对四种情形进行分析比较，从表4可以看出，安装节点都安装光伏机组时年购电费用最少，相比情形一少了49.29万元，相比情形二少了8.83万元，相比情形三少了16.26万元。由此可以看出，分布式电源的接入可以有效优化电网系统的经济性，并在实际生活中，不同地区有着不同的气候环境，也会影响分布式电源的安装。

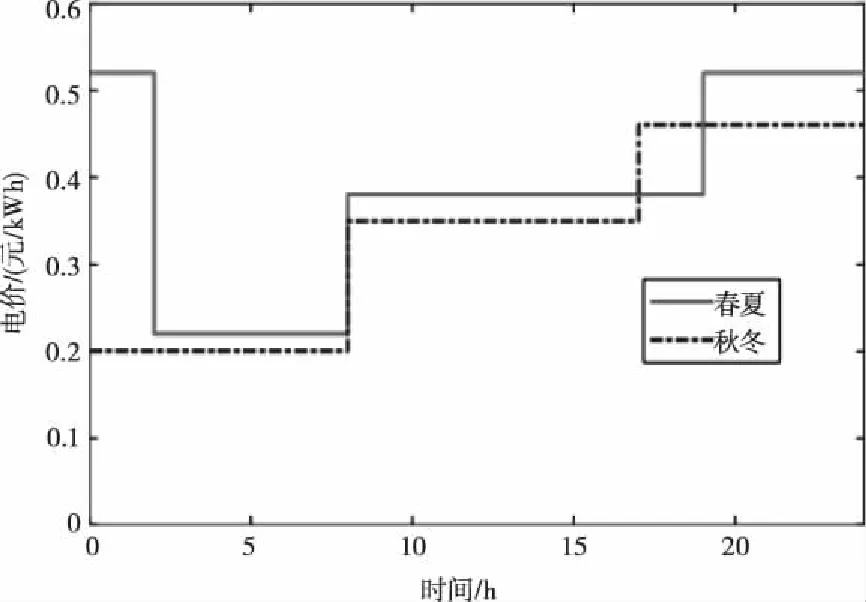
图10 四季分时电价

表4 年购电费用比较

综上所述，在考虑新能源出力和负荷不确定性的情况下，对电网系统合理的加入分布式电源后，可以很好地改善系统的电压幅值、有功损耗及年购电费用，为配电网的运行提供了更为安全经济的环境。

6 结语

文中提出了一种考虑风光出力及负荷不确定性的主动配电网分布式电源(DG)双层规划方法，并在IEEE33节点系统进行仿真分析。结论如下：

1) 根据光照强度和风速算出风光的出力期望，为后续考虑风电不确定性奠定了基础。

2) 建立分布式电源双层规划模型，上层模型的目标函数是系统的网络有功损耗；下层模型是根据分布式电源的节点电压稳定性指数、投资效益指标建立多目标优化规划数学模型来确定安装容量。

3) 根据双层规划模型得到了分布式电源的处理位置与容量。加入出力不确定的新能源后，分两阶段对模型进行分析，第一阶段考虑风电接入对电网系统的安全性影响，第二阶段对风电接入不同情形下的电网系统基于分时电价的经济性进行分析。提出的模型能有效的优化主网的安全性与经济性。其规划模型及求解方法可为其它类似规划问题提供参考，有利于运行人员选择更好的分布式电源接入方案。