Nonisothermal dissolution kinetics on Mg17Al12 intermetallic in Mg-Al alloys

Renhai Shi

a Beijing Advanced Innovation Center for Materials Genome Engineering,Institute for Advanced Materials and Technology,University of Science and Technology Beijing,Beijing 100083,China

bMaterials Science and Engineering,The Ohio State University,Columbus,OH 43210,USA

Abstract In this work,nonisothermal dissolution of intermetallic Mg17Al12 in Mg-Al alloy has been firstly studied via Differential Scanning Calorimetry-DSC,X-Ray Diffraction-XRD and Scanning Electron Microscope-SEM as well as CALPHAD_based dissolution models and molecular dynamics simulation.The size and volume fraction of Mg17Al12 phase could be predicted via the present kinetic dissolution model and agree well with experimental results.Also,the data-driven screening calculation shows that there is a range of temperature for significantly dissolving Mg17Al12 phase,which could be increased with the increase of heating rate.The evolution of structural order for Mg17Al12 phase has also been performed via molecular dynamics simulation with LAMMPS.The simulated results indicate that the structural order of Mg17Al12 phase during heating is mainly affected by the Al-contained atomic pairs (Al-Al and Al-Mg),suggested that Mg atoms are thermodynamically and kinetically more active than Al atoms in Mg17Al12 phase during heating,which has also been approved via the calculated atomic mobility of Mg and Al atoms in Mg17Al12 phase in this work.Therefore,the atomic mobility of Mg atoms is mainly attributed to the interdiffusion coefficient of Mg17Al12 phase which determines the dissolution of Mg17Al12 phase during heating.The fundamental principle in this work could be used for other intermetallics and offers the greatly valuable information for optimizing the thermal processing in application of metal structural materials.

Keywords: Mg-Al alloy;Intermetallics;Dissolution model;CALPHAD;Molecular dynamics simulation.

1.Introduction

Lightweight structural metal materials have attracted great attention for engineering applications in auto-motive and aerospace industries.Magnesium (Mg),the lightest structural metal,and its alloys are prime candidates for such applications [1] due to their lightweight,excellent casting capability and highly specific stiffness.Aluminum (Al),one of lighter structural metals,constitutes the main alloying element to improve the mechanical properties,enhance die castability and corrosion resistance of Mg alloys at room temperature [2–4].

In Mg-Al alloys,the intermetallic Mg17Al12phase with low eutectic temperature is the dominant precipitate phase[5,6].It can significantly influence corrosion [7–9],wear[10] and mechanical properties [2,5,11–13] of Mg-Al alloys.The presence or absence of Mg17Al12precipitates has a great influence on the grain structure upon the hot deformation,and hence affects the strength of the deformed alloy.For example,the Mg17Al12particles along grain boundaries at elevated temperature can effectively pin grain boundaries for grain refinement and relax the intergranular stress to facilitate grain boundary slides behavior [13].However,the nonisothermal dissolution modelling of intermetallic Mg17Al12phase is not well developed and the mechanism during its dissolution is also not understood yet.Therefore,a quantitative prediction of dissolution kinetics taking into account the evolution of size and volume fraction of Mg17Al12phase during heat treatment should be very useful for the optimization of processing.It is also of great significance to explore the mechanism of dissolution of intermetallic Mg17Al12phase during dissolution treatment.

Extensive research has been reported that CALPHAD(CALculation of PHAse Diagrams) modeling [14–21],as a part of Integrated Computational Materials Engineering(ICME) [22] framework,has been successfully applied to study the alloying-processing-structure-property relationships in multicomponent alloy system.DICTRA (DIffusion Controlled TRAnsformation) [23] part of CALPHAD has been developed and successfully used to study the diffusioncontrolled phase transformation,based on the reliable thermodynamic and kinetic databases,such as the dissolution of NbC into steelEQ70 [24],formation of (Ti,Ta,Nb,W)(C,N) layers on surface of the cemented carbide [25]and dissolution of Mg2Si in AA6063 [26].Although the isothermal dissolution behavior of Mg17Al12phase in Mg alloys have been studied via experiments and several analytical models [9,27–30],the nonisothermal dissolution mechanism of Mg17Al12phase is not fully understood due to lack of the reliable the thermodynamic and kinetic databases and reasonably considering the influence of geometry of Mg17Al12on its dissolution.Also,the influence of heating rate during the pre-heat treatment on the size and volume fraction of Mg17Al12phase is not yet reported.Therefore,this work will study the non-isothermal dissolution behavior of Mg17Al12phase via DICTRA with our recently developed thermodynamic and kinetic databases for both Mg-(hcp) and Mg17Al12phases [31].The influence of geometry of Mg17Al12phase on its dissolution will also be studied.The data-driven screening technique enables the tracking of size and volume fraction of Mg17Al12phase under different heating rate.In order to discover the dissolution mechanism of Mg17Al12phase,the evolution of structural order of Mg17Al12phase during heat treatment will be studied and the movement of Mg and Al atoms will be tracked via molecular dynamics simulation.

2.Materials and methods

2.1.Experiments

Binary Mg-10wt%Al alloy was prepared from pure Mg(99.99 wt%) and Al (99.9 wt%) in a steel crucible under a protective gas mixture of CO2and SF6and cast at 750°C into a steel mold preheated to 400°C to produce 110×110×18mm plate.Samples with dimension of 20×20×3mm were taken from the middle of the plate and completely solutionized at 420°C from the calculated Al-Mg binary phase diagram [31].Then the solutionized samples were isothermally aged at 200°C and 48hrs to introduce the precipitate particles (Mg17Al12).In order to observe the dissolution of the precipitate particles (Mg17Al12),the dissolution experiment was conducted via heating the aged samples starting from 25°C with heating rate 5°C/min.The samples were characterized at 25°C,130°C,230°C,330°C,and 450°C,respectively,to observe the dissolution of precipitate particles.These temperatures in experiments were selected from the phase diagram of Mg-10wt%Al [31].All the abovementioned heat treatments were conducted in the KSL-1200X muffle furnace.

The surface of samples was mechanical ground on SiC papers up to 1200 and polished down to 0.05μm colloidal silica finish.The samples were then etched by solution (1.5g picric acid+1.25ml acetic acid+25ml ethanol+2.5ml distilled water) for the observation of an optical microscope (Zeiss Axio Observer A1-OM).The non-etched samples were performed via a scanning electron microscope(FEI Apreo LoVac SEM).The identification of phase was conducted via X-Ray Diffraction analysis with an X-ray diffractometer (Rigaku Ultima IV) with Cu Ka radiation.The 2θrange of 20 to 90deg with 0.02deg incremental step was used to acquire precise diffraction patterns.The volume fraction and width of intermetallic compound and grain size were measured by an image analysis software (Image pro plus) based on the SEM and OM images,respectively.For each sample,at least five photographs were randomly selected for the quantitative analysis.The aged sample (～5mg) was also in-situ treated in the Differential Scanning Calorimeter (DSC) equipment starting from 25°C with heating rate 5°C/min to obtain the experimental heat flow via following the same heat procedure of the dissolution of precipitate in this work.

2.2.Kinetic dissolution modeling

It is proposed that the dissolution of intermetallic (IMC)phase can be controlled by diffusion of the component toward or away from the interface,and the flux of the component can be calculated by the flux balance equation based on the mass conservation law [32]:

Wherek=1,2,…,n,referring to different components;VmatrixandVIMCare the interface migration rates of matrix and intermetallic phases,respectively;are the concentrations of the componentkin matrix and intermetallic phases close to the phase interface;are the diffusion fluxes in matrix and intermetallic phases.

The multi-component diffusion theory was applied to describe the fluxes of species driven by a concentration gradient[33].The law relating the flux and concentration gradient is given by the multi-component extension of Fick’s first law:

WhereJkis the flux of specieskin the direction of thez-axis andis the concentration gradient of species.is the diffusivity or the interdiffusion coefficient of specieskand depends on concentration and temperature.

By considering the influence of geometry of one phase on the fluxJk,the variation in time of the fluxJkof componentkcan be obtained from the solution of the equation of continuity as followed:

WhereNSrepresents the number of atoms on sublatticesper formula unit of one phase.Vmis the molar volume defined as the volume of an amount of the phase which contains one mole of formula unit.is the site fraction of componentkin sublattices.is the diffusional fluxes of componentkin sublatticesof one phase.mis geometrical factor in whichm=0 is planar symmetry,m=1 is cylindrical symmetry andm=2 is spherical symmetry [34].

Eq.(3) gives the fundamental differential equation of diffusion:

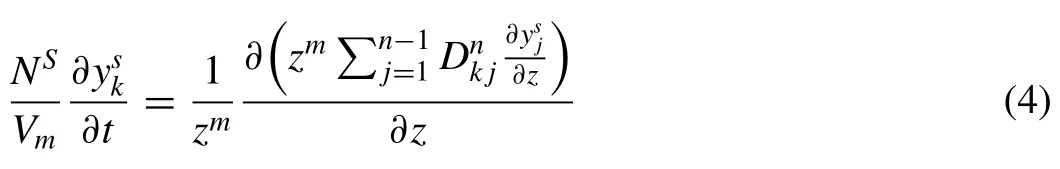
Where the diffusion coefficient matrixDnk jis a product of two matrices;one consisting only of pure thermodynamic information and one consisting of the so-called mobilities,and can be expressed as follows:

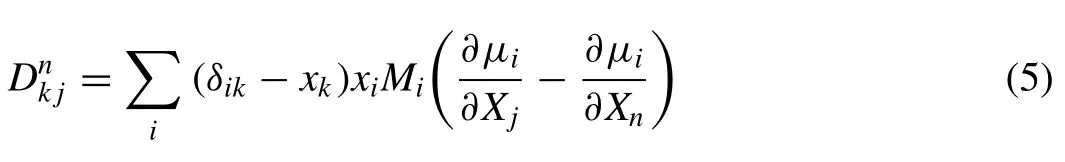
Herexkis the mole fraction of elementkand μiis the chemical potential of the elementi,andnis an arbitrary chosen reference element.δikis the Kronecker delta;i.e.δik=1 whenj=kandδik=0 otherwise.

By absolute-reaction theory argumentation [33],the mobility parameterMk,for an elementkin a given phase,can be divided into a frequency factorand an activation energy factorQk:

WhereRis the gas constant andTis the absolute temperature.andQkare not constant;hence their values depend on temperature,pressure,and composition.

Thus,the dissolution process can be simplified to the diffusion of the component and interface migration rate can be obtained by calculating the related phase equilibria and solving the flux and diffusion equation,which can be performed in a general software package-DICTRA (DIffusion Controlled TRAnsformation) [35] coupling with reliable thermodynamic and atomic diffusion databases [31].It should be noted that both discontinuous and continuous Mg17Al12precipitates have the same crystallographic features (Body-Centered Cubic crystal) and predominant orientation relationship (OR) with Mg matrix from the previous research[36–40].For the sake of simplicity,the dissolution mechanism of both phases is assumed the same in the present dissolution modeling.

2.3.Molecular dynamic simulation (MD)

In order to reveal the dissolution mechanism and dynamic behavior of Mg17Al12phase during the heat treatment,classical MD calculations were performed using a large-scale atomic/molecular massively parallel simulator,LAMMPS [43].A semi-empirical embedded atom potential(EAM),developed by Zhang and Kelly [44],was used to describe the interatomic interactions in Mg-Al system,in which the total energy of the system can be written as

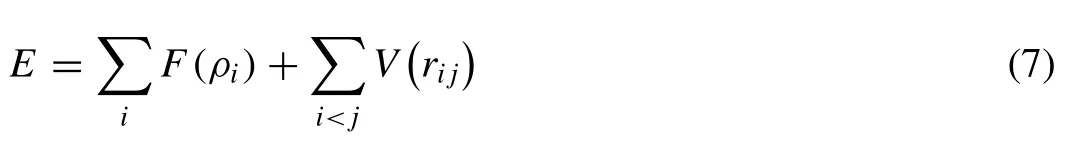
WhereV(rij) is the pairwise interaction potential between atomsiandjat separationrij,andF(ρi) is the embedding energy that is required to embed atomiinto the system consisting of other atoms,ρiis the total atomic density at atomidue to surrounding atoms

Here,is the contribution to the atomic density from atomjat atomiposition.

In present work,a simulation box with 26 × 26 × 26 unit cells (34 Mg atoms and 24 Al atoms in each unit cell) was constructed.Periodic boundary conditions were applied in the x-,y-,z-directions of the simulation box and the system initial temperature was equilibrated at 25 °C.The system was then allowed to heat to 230°C,350°C,380°C and 400°C,respectively.These temperatures in MD simulation were selected from the validated dissolution modeling so as to clearly show the energetic and structural evolution of Mg17Al12phase.For each temperature,the system was equilibrated under isothermal isobaric ensemble (NPT) for 5 ×105time steps and then run under canonical ensemble (NVT) for 1 ×104time steps.Each timestep is equal to 0.01ps.Finally,the configurations,atom arrangement and the relevant properties were extracted at the equilibration stage of each temperature for further investigations.

Table 1 Atom position [41] in Mg17Al12 phase.

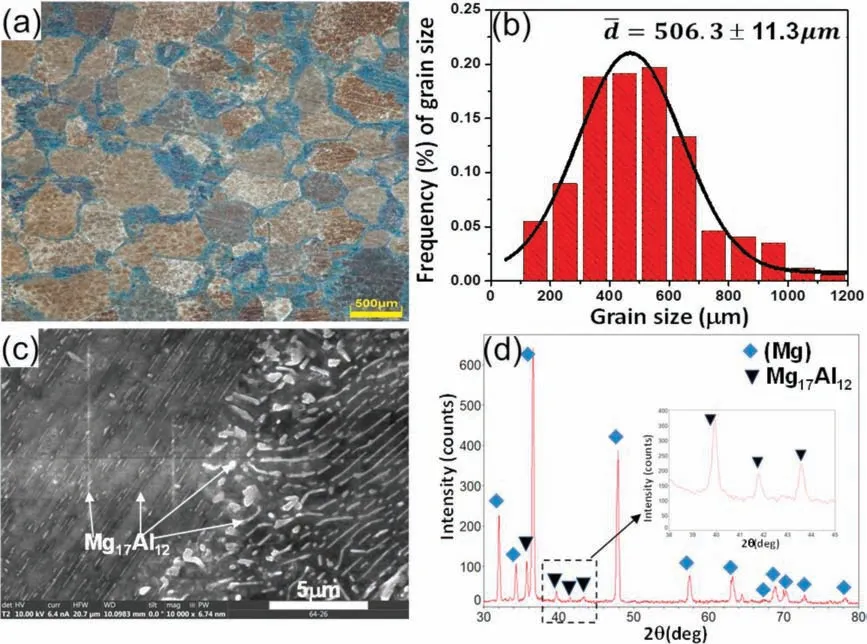
Fig.1.The Mg-10Al samples aged at 200 °C: (a) optical micrograph;(b) its corresponding grain size distribution;(c) SEM micrograph;(d) XRD result inserted with local angle range (38–45,deg.).

3.Results and discussion

3.1.Experimental observation

The initial microstructure of the Mg-10Al aged at 200 °C has been carried out via optical microscope,SEM and XRD techniques in Fig.1(a)-(d).Fig.1(a) shows the initial microstructure of the aged Mg-10Al sample with average grain size about 506.3 μmin Fig.1(b).It should be noted that the blue region in Fig.1(a) is supposed to be the region near grain boundary with eutectic phases and the segregated solutes and the brown region is supposed to be the grain.The different color in contrast could be caused by the reaction of the etched solution used in this work.The SEM micrograph in Fig.1(c) shows that the lamella phases with sub-micron size exist in Mg matrix and has been confirmed as Mg17Al12phase via XRD in Fig.1(d).

The dissolution of the aged Mg-10Al samples has been performed at heating rate 5 °C/min starting from 25 °C.The microstructure of the aged Mg-10Al has been characterized via SEM at several temperatures shown in Fig.2.Fig.2(a)–(e)shows that the Mg17Al12phase has been dissolved when the temperature is increasing.The lamella Mg17Al12precipitate has been significantly dissolved at 450 °C.The experimental observation has a good agreement with the XRD results shown in Fig.2(f),in which the Mg17Al12phase cannot be significantly observed in X-Ray patterns.

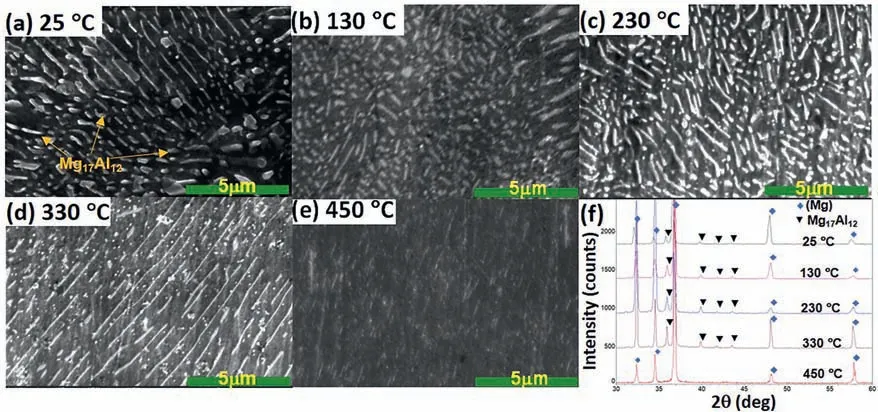
Fig.2.The dissolution evolution of Mg17Al12 phase in the aged Mg-10Al alloy at 5 °C/min heating rate: (a) at 25 °C;(b) 130 °C;(c) 230 °C;(d) 330 °C;(e) 450 °C and (f) XRD results.

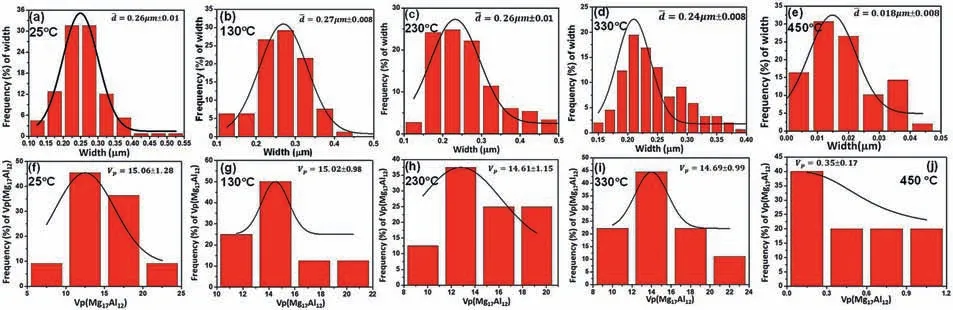
Fig.3.The evolution of width and the effective volume fraction of lamella Mg17Al12 phase during heating rate 5°C/min at temperatures: (a) 25 °C;(b) 130°C;(c) 230 °C;(d) 330 °C;(e) 450 °C.Noted that the effective volume fraction was measured as the average area fraction from Fig.2.

The width and the effective volume fraction of Mg17Al12phase in aged Mg-10Al alloy at 5 °C/min heating rate have been quantitatively analyzed at several temperatures and shown in Fig.3.When temperature heats from 25 °C to 230°C,the width of Mg17Al12phase have slightly changed in Fig.3(a)–(c).However,when temperature heats to 330 °C in Fig.3(d),the width of Mg17Al12phase starts to decrease and significantly decreases at 450 °C.Similar results have been observed for the effective volume fraction of Mg17Al12phase in Fig.3(f)–(j).It should be noted that the average width of Mg17Al12phase was measured from different location including inside of grain and near grain boundary on the samples and used for the present dissolution model as an initial condition.Also,the present dissolution model is based on the 1D DICTRA simulation which assumes the 1D diffusion along the width direction of lamella phase.Thus,only the width of both Mg matrix and Mg17Al12phase are considered and other directional sizes are assumed the same for the 1D DICTRA model.For this purpose,the effective volume fraction of lamella phase is assumed as the average area fraction of lamella phase measured from Fig.2 for the validation of the present dissolution model.

3.2.Kinetic dissolution modeling

In order to study the influence of geometry of Mg17Al12(γ) phase on its dissolution,one dissolution model has been constructed in this study to compare with other two dissolution models generally used in the study of dissolution of intermetallics.These three dissolution models are named as CASE-1,CASE-2 and CASE-3,thereafter,in this work.

In CASE-1:

(1) Mg17Al12phase is assumed as planar symmetry with a width (Lγ);the local matrix (Mg) is taken as a planar symmetry with a width (LMg) shown in Fig.4(a).The length (b) and thickness (c) for both phases are assumed as the same.The relationship between the volume fraction of Mg17Al12and the width of matrix is given as:

Whereis the volume fraction of Mg17Al12phase;VγandV,respectively,are the molar volumes of Mg17Al12phase and the cell.Lγandare experimentally measured in this work shown in Fig.3(a) and (f).

Fig.4.The kinetic dissolution models of Mg17Al12 phase at aged Mg-10Al alloy: (a) CASE-1 and (b) CASE-2&3.

(2) The Mg17Al12is considered as a diffusion phase with an interdiffusion coefficient as a function of temperature and composition,calculated from our recently developed thermodynamic and kinetic databases [31].

In CASE-2,it has a similar assumption like CASE-1,except for:

(1) Mg17Al12and the matrix (Mg) phases are both assumed as planar symmetry with a width of (Lγ) and(RMg),respectively,in Fig.4(b).ButLγis calculated via Eq.(9) based on the experimentally measuredin Fig.3(f) and radius (RMg) of one Mg grain in Fig.1(b),rather than local (Mg) size.

(2) The Mg17Al12is considered as a stoichiometric and non-diffusion phase due to lack of interdiffusion coefficients for most intermetallics.

In CASE-3:

(1) Mg17Al12and the matrix (Mg) phases are both assumed as a spherical symmetry with a radius ofRγandRMg,respectively,in Fig.4(b).The relationship between the volume fraction of Mg17Al12and the radii of Mg17Al12and one Mg grain is given as:

However,theRγis calculated via Eq.(10) based on the experimentally measuredin Fig.3(f) and radius (RMg) of one Mg grain in Fig.1(b),rather than local (Mg) size.

(2) The Mg17Al12is considered as stoichiometric and nondiffusion phase due to lack of interdiffusion coefficients for most intermetallics.

The initial composition profile in these three kinetic dissolution models could be calculated at aged temperature 200°C via Thermo-Calc software.

Fig.5 shows the evolution of dissolution for Mg17Al12phase during the heating.DSC measurement in Fig.5(a)shows one peak between 200 °C and 500 °C.Based on the result of XRD in Fig.2(f),this peak is corresponding to the phase transformation of Mg17Al12to Mg(Hcp).The onset temperature is around 280 °C and the peak temperature is around 380 °C.Also,the dissolution rate of Mg17Al12phase during heating has been calculated via these three kinetic models followed by DSC procedure in Fig.5(a).The calculated results show that the onset and peak temperatures from the present dissolution model (CASE-1) have a good agreement with DSC measurement,however,the onset and peak temperatures from CASE-2 and CASE-3 models generally used in most research are much higher than the DSC measurement.Similar results have been observed in the prediction of width and volume fraction of Mg17Al12phase in Fig.5(b)-(c).The reason could be that CASE-2 and CASE-3 models may consider improper assumptions such as the overestimated initial width and shape of Mg17Al12phase.Therefore,it is great significance of reasonable assumption for the kinetic dissolution modeling which should be varied for different kinds of intermetallic phases.For lamella Mg17Al12phase in Mg-Al system,the calculated results via the CASE-1 model constructed in this work could have a good agreement with the heat flow from DSC and with the width and volume percent from SEM.

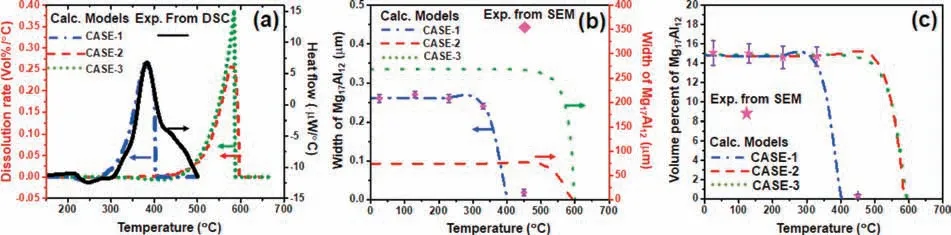
Fig.5.The evolution of dissolution for Mg17Al12 phase during heating: (a) the calculated dissolution rate of Mg17Al12 phase from three kinetic dissolution modelings,superimposed with the experimental heat flow from DSC;(b) and (c) calculation of width and volume percent of Mg17Al12 phase during heating from three kinetic dissolution modelings,superimposed with the experimental data.

Fig.6.Data-driven screening the evolution of dissolution for Mg17Al12 phase as a function of heating rate via present kinetic dissolution model (CASE-1):(a) volume fraction and (b) width.

Via integrating the present dissolution model (CASE-1)with thermodynamic and diffusion databases of Mg17Al12phase from our recent work [31],the evolution of dissolution for Mg17Al12phase at various heating rate could be predicted.Fig.6(a)–(b),respectively,show the calculated volume fraction and width of Mg17Al12phase during different heating rates between 0.1 °C/min and 100 °C/min.The calculated results show that the onset temperature of dissolution for Mg17Al12phase is increased with the increase of heating rate.Also,there exists a range of temperature for the dissolution in which the Mg17Al12phase could be significantly dissolved.This kind of temperature range could offer the significantly important information in the thermal history,especially in hot-deformed processing of materials.

Fig.7 shows the calculated interdiffusion coefficient and atomic mobility of solute Mg and Al in Mg17Al12phase as a function of temperature.The calculated results show that the interdiffusion coefficient is significantly increased starting around 280 °C,closed to the experimental onset temperature of dissolution for Mg17Al12phase from DSC in Fig.5(a).The similar result has been observed for the atomic mobility of solute Mg in Mg17Al12phase.However,the atomic mobility of solute Al is not obviously changed during the heating.It suggests that the atomic mobility of solute Mg is mainly attributed to the interdiffusion coefficient,which determines the dissolution of Mg17Al12phase during the heating.

3.3.Molecular dynamics simulation

Fig.8 shows the calculated kinetic energy per atom in Mg17Al12phase between 25 °C and 400 °C via molecular dynamics simulation with LAMMPS.Fig.8(a) shows the simulation system of Mg17Al12phase at 25 °C.Fig.8(b)–(f) shows the kinetic energy for Mg and Al atoms at different temperatures in (10) plane,which contains all possible close packed or nearly close packed directions [42].Fig.8(b)presents that the kinetic energy for each Mg and Al atom in(10) plane at 25 °C is quite low,especially at the closed direction [111] and [110].With the increase of temperature in Fig.8(c)–(f),the kinetic energy of most Mg atoms is significantly increased.However,the kinetic energy of most Al atoms is slightly increased.It suggests that the Mg atom is more active in Mg17Al12phase with the increase of temperature,which has a good agreement with the calculated atomic mobility in Fig.7 via CALPHAD_based diffusion models.

Fig.7.The calculated interdiffusion coefficient and atomic mobility of solute Mg,Al in Mg17Al12 (γ) phase as a function of temperature via DICTRA with our developed thermodynamic and diffusion databases [31].

Fig.8.Configuration of Mg and Al atoms with kinetic energy in Mg17Al12 phase: (a) in a simulation box;(b)–(e) in a (10) plane of the simulation box at different temperatures: (b) 25 °C,(c) 230 °C,(d) 350 °C,(e) 380 °C and (f) 400 °C.Note that the small size particle with dash circle represents Al atom and big size particle without dash circle is Mg atom.The color of each atom means the atom’s kinetic energy and the scale of color bar is shown in Fig.8(a).

Fig.9.(a) histogram of all atoms with kinetic energy in the simulation box and (b) the lattice constant,coefficient of linear thermal expansion (CLE),mean free path (MFP) of Mg/Al atom in Mg17Al12 phase at different temperatures.

With the increase of temperature,the number of atoms with different kinetic energy has been calculated and shown in Fig.9(a).The calculated results show that the total number of atoms with kinetic energy is increased and the average kinetic energy per atom is also increased with the increase of temperature.It suggests that the more atoms have been activated to move in Mg17Al12phase at higher temperature.Also,the mean free path(MFP)of Mg and Al atoms in Mg17Al12at various temperatures has been calculated in Fig.9(b) via the simplified Brownian motion equation:λiin whichλi,Diandare the MFP,self-diffusion and average velocity of atomiand calculated from the present MD simulation.The resulting simulation shows that MFP of Mg atom is significantly increased during heating and larger than MFP of Al atom,which is slightly enhanced.Based on the results from Figs.8 to 9(b),it can conclude that more Mg atoms can be activated to diffuse in Mg17Al12phase during heating.The lattice constant and the coefficient of linear thermal expansion (CLE) of Mg17Al12phase as a function of temperature have also been calculated in Fig.9(b).The results show that lattice constant of Mg17Al12phase gradually increased with the increase of temperature.As an extensive property,volume is normalized to the volume of unit cell (Vuc(T) in a periodic simulation.The volume per unit cell at atmosphere pressure for non-magnetic materials could be similar to the molar volume [45] expressed as:

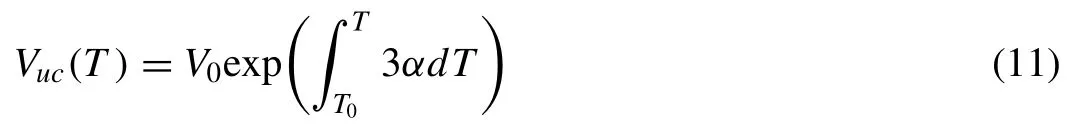
WhereV0is the volume of unit cell at the reference temperatureT0,αdenotes the CLE of a phase in the non-magnetic state.3αrepresents volume expansion coefficient that can be expressed using a simple polynomial function [45]:

Where a,b and c are constant coefficients and can be evaluated by fitting to the lattice constant data.Thus,the CLE of Mg17Al12phase can been fitted as:

In order to examine the structures of Mg17Al12phase during heating,the total pair distribution function (PDF) and partial PDFs are calculated and illustrated in Fig.10.The partial PDF [46] is expressed as:

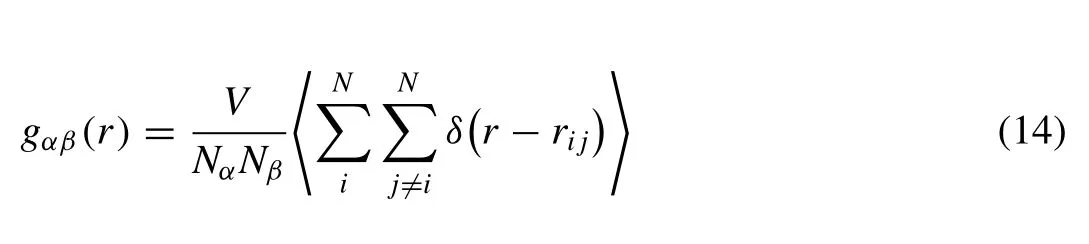
WhereVis the volume of the system,andNαandNβare the number of atomsαandβ,respectively.δ(r-rij) is the Dirac delta function,and the angular brackets represent the time average.From the PDFs,we could determine the nearest neighbor shell and coordinate numbers.

All total and partial PDFs exbibit sharp and prominent first peaks in Fig.10(a),(c),(e) and (g).The intensity of first peak of all PDFs decreases with increase of temperature.In Fig.10(b),(d),(f) and (h),partial PDFs of Al-Mg and Mg-Mg pairs show two sub-peaks in second peak except for total PDF and partial PDF of Al-Al pair with three sub-peaks at 25 °C.It suggests that the splitting second peak of total PDF is mainly caused by splitting second peak of partial PDF of Al-Al pair.It should be noted that the prominent split in the second peak of each system indicates the presence of medium-range order (MRO) and has been recorded as consequence of local ordering[47,48].With the increase of temperature,the three sub-peaks of second peak of total PDF turns into two sub-peak and the splitting of second peak of partial PDF of Al-Al,Al-Mg and Mg-Mg are weakened.It should be noted that the splitting of second peak of Mg-Mg pair is almost disappeared and the intensity is much lower than other pairs to show the possibility of disorder.Therefore,the order of structure of Mg17Al12phase is mainly determined by the Al-related pairs(Al-Al and Al-Mg)and Al solute is suggested to be thermodynamically and kinetically more stable than Mg atom,which has a good agreement with the calculated atomic mobility via CALPHAD_based diffusion model in Fig.7 and with MFP of Mg and Al atoms in Fig.9(b).Therefore,it can conclude that Mg atoms are more active than Al atoms in Mg17Al12phase during heating and are mainly attributed to the interdiffusion coefficient which determines the dissolution of Mg17Al12phase.

Fig.10.PDFs for Mg17Al12 phase at various temperatures: (a) the total PDFs of the whole system;(c),(e) and (g) partial PDFs of Al-Al,Al-Mg,and Mg-Mg pairs,respectively;(b),(d),(f) and (h) the enlarged total and partial PDFs.

4.Conclusions

Nonisothermal dissolution of intermetallic Mg17Al12in Mg-10Al alloy has been studied via experimental observation as well as via CALPHAD_based dissolution models and molecular dynamics simulation.

(1) The evolution of microstructure and phase transformation of lamella Mg17Al12phase during heating has been observed via experimental analysis with DSC,XRD and SEM in this work.

(2) A reasonable kinetic dissolution model (CASE-1) has been constructed and clarified in this study.Compared with the usually used dissolution models (CASE 2&3),the prediction via the present kinetic dissolution model(CASE-1) has a much better agreement with the experimental results.

(3) The data-driven screening calculation at heating rates between 0.1 °C/min and 100 °C/min has been performed via integrating the present dissolution model(CASE-1) and databases of thermodynamics and kinetics for both Mg(Hcp)and Mg17Al12phases.The screening results show that a thermal window of significantly dissolving Mg17Al12phase exists between 250 °C and 400 °C and increases with the increase of heating rate.

(4) The structural order for Mg17Al12phase during heating process has also been studied via molecular dynamics simulations with LAMMPS.The calculated results show that the kinetic energy of Mg atoms is significantly enhanced,and the Mg17Al12phase is positively thermal expansion when the temperature is increased.The structural order of Mg17Al12phase during heating is mainly affected by the Al-related atomic pairs (Al-Al and Al-Mg),which suggests that Mg atoms are thermodynamically and kinetically more active than Al atoms in Mg17Al12phase.

In short,the nonisothermal dissolution of Mg17Al12phase is mainly dependent on its interdiffusion coefficient,which is mainly attributed to the increase of atomic mobility of Mg atoms in Mg17Al12phase during heating.Therefore,understanding the mechanism of dissolution of intermetallic phases will assist in revealing the relationship of processing and microstructure and then optimizing the thermal processing for the design of metallic materials.

Declaration of Competing Interest

The author declares that there is no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The author gratefully acknowledges Prof.Alan Luo (Ohio State University) for supporting the experimental research,Prof.John E.Allison and Dr.Tracy D.Berman (University of Michigan,Ann Arbor) for discussion of kinetic dissolution models,Dr.F.X.Wang (Virginia Polytechnic Institute and State University) and Dr.P.Chen (Texas A&M University) for the discussion of Molecular dynamic simulations.Finally,the author is grateful for the support from Fundamental Research Funds for the Central Universities under Award Number 06500161.