Anthropomorphic hand based on twisted-string-driven da Vinci’s mechanism for approaching human dexterity and power of grasp

Yong-bin JIN, Shao-wen CHENG, Yan-yan YUAN, Hong-tao WANG, Wei YANG

Research Article

Anthropomorphic hand based on twisted-string-driven da Vinci’s mechanism for approaching human dexterity and power of grasp

1Center for X-Mechanics, Zhejiang University, Hangzhou 310027, China2ZJU-Hangzhou Global Scientific and Technological Innovation Center, Zhejiang University, Hangzhou 311200, China3State Key Laboratory of Fluid Power and Mechatronic System, Zhejiang University, Hangzhou 310027, China4Institute of Applied Mechanics, Zhejiang University, Hangzhou 310027, China

Designing anthropomorphic prosthetic hands that approach human-level performance remains a great challenge. Commercial prosthetics are still inferior to human hands in several important properties, such as weight, size, fingertip force, grasp velocity, and active and passive dexterities. We present a novel design based on the under-actuated da Vinci’s mechanism driven by a flexible twisted string actuator (TSA). The distributed drive scheme allows structural optimization using a motion capture database to reproduce the natural movement of human hands while keeping adaptability to free-form objects. The application of TSA realizes a high conversion from motor torque to tendon contraction force while keeping the structure light, flexible, and compact. Our anthropomorphic prosthetic hand, consisting of six active and 15 passive degrees of freedom, has a weight of 280 g, approximately 70% of that of a human hand. It passed 30 of the 33 Feix grasp tests on objects in daily living and retained a loading capacity of 5 kg. This simple but intelligent mechanism leads to excellent stability and adaptability and renders feasible wide applications in prosthetics and in service robots.

Anthropomorphic hand; da Vinci’s mechanism; Twisted string actuator (TSA); Intelligent mechanism; Principal component analysis (PCA)

1 Introduction

Dexterous and powerful robot hands are essential for humanoid or service robots, especially those which are designed to handle unstructured objects in the human daily living environment (Billard and Kragic, 2019). For pick-and-place tasks, most widely used end effectors are vacuum grippers or parallel jaw grippers. The grippers generally have one degree of freedom (DOF), which is suitable for the grasping of structured objects, but difficult for grasping objects with irregular shapes. A specially designed kinematic planning and control algorithm is critical (Mahler et al., 2017) for a robust grasp of a wide range of daily objects. Soft grippers are generally employed to improve adaptability (Shintake et al., 2018). For example, increasing the maximum deformation of the gripper (Brown et al., 2010; Ruotolo et al., 2021) and the contact area between the gripper and object (Li et al., 2019) is very effective in adapting vacuum grippers to various objects. For the same purpose, the rigid fingers of the single-DOF parallel jaw grippers are replaced with flexible structures such as the fin ray structure (Yang et al., 2021), fluidic elastomer actuators (Galloway et al., 2016), and the variable stiffness mechanism (Firouzeh and Paik, 2017). However, the few active DOFs significantly limit the modes of grasp and wide application in real life.

An anthropomorphic robot hand is a natural aspiration for robots to approach human-level dexterity. Two different schemes are employed. For high-dexterity applications, dozens of actuators are integrated in the forearms (Grebenstein et al., 2010; Schmitz et al., 2010; Xu and Todorov, 2016) to achieve multimode grasp and even complex in-hand manipulation tasks (Rajeswaran et al., 2018; Andrychowicz et al., 2020; Yang et al., 2022). On the other hand, modular design with fewer actuators is adopted as a compromise between compactness and dexterity (Liu et al., 2008; Lee et al., 2017; Laffranchi et al., 2020). It benefits both prosthetics and some robotic systems. For all types of robot hands, the overall performance highly depends on the actuation systems. In the limited space, electric motors with smaller volume are almost the only choice and they limit the power output. As a replacement, high-power-density artificial muscles have been proposed, such as super-coiled polymers (Yip and Niemeyer, 2015; Oh et al., 2022), shape memory alloy (Andrianesis and Tzes, 2013), fluidic actuators (Deimel and Brock, 2016; Zhao et al., 2016), air chambers (Chen and Zou, 2021; de Pascali et al., 2022; Shorthose et al., 2022), and dielectric elastomer actuators (Jung et al., 2006). At present, artificial muscles still suffer from slow response, short working life or a requirement in practice for assistance from external devices.

An alternative route is to design intelligent transmission mechanisms to meet the needs of robot hands for dexterity, compactness, and power. Currently, intensive studies are being focused on achieving dexterity and compactness, while sacrificing power. It is noted that the movements of the joints of human hands are strongly coupled (Santello et al., 1998; Weiss and Flanders, 2004; Cobos et al., 2010; Liu et al., 2016). Based on this key observation, dexterous and compact anthropomorphic hands have been devised with complicated transmission mechanisms (Xu et al., 2014; Xiong et al., 2016; Liu et al., 2017), allowing multiple joints to be actuated cooperatively. In such a design, the high passive DOFs are crucial in attaining dexterity, while the lower active DOFs ensure compactness. Realization of the preferred coupling of various joints would involve complicated mechanical mechanisms, such as gears (Xu et al., 2014), pulleys (Xiong et al., 2016), and linkage transmission (Liu et al., 2017; Kim et al., 2021), which consequently increase the complexity of the robot hand, as well as the difficulty of assembling it. In contrast, flexible twisted string actuators (TSA) are a simple, compact, and light weight linear actuation system (Palli et al., 2013; Gaponov et al., 2014). In particular, the high reduction ratio results in a large contraction force even when driven by a small electric motor (Shin et al., 2012; Jeong et al., 2017; O'Brien et al., 2018; Liu et al., 2021). Here, we present an anthropomorphic prosthetic hand design based on under-actuated da Vinci's architecture driven by TSA, in which a tendon passes through a series of attachment points on the phalanxes of a finger. By optimizing the positions of the attachment points and the joint stiffness, the robot hand can approximately simulate the anatomy of the human hand and reproduce its characteristic movements. Moreover, the TSA realizes a high conversion from motor torque to tendon contraction force while keeping the structure light, flexible, and compact.

To maximize dexterity, the da Vinci's mechanism of every finger is optimized independently according to a human hand database (Santello et al., 1998). The flexible and compact transmission makes it possible to integrate all components in a 3D-printed human-size robot hand. Our robot hand weighs 280 g, approximately 70% of a human hand. Grasp tests have been performed on daily living objects according to the taxonomy of Feix et al. (2016). Our robot hand can pass through 91% of the grasp tests. The tests also show the excellent adaptability of the robot hand to the size and shape of the object. The fastest grasp speed is 142 (°)/s, approximately 83% of human-level performance. The attainable maximum fingertip force is 8.3 N, about 54% of human-level performance. The power grasp tests show that the robot hand can lift a weight of 5 kg. Both the size of the modular design and the overall performance are comparable to human hands, which guarantees the feasibility of wide application of our anthropomorphic robot hand in prosthetics and service robots.

2 Methods

2.1 Modeling of da Vinci’s mechanism

The main idea of the da Vinci's mechanism is to reproduce the bending characteristics of human hands without employing a complex physiological structure. Fig. 1 shows the kinematic model of da Vinci's mechanism, as a mechanical mimic of the human finger anatomy. The length of each bone is noted asL(=1‍–4). The distal interphalangeal (DIP) joint, proximal interphalangeal (PIP) joint, and metacarpophalangeal (MCP) joint are simplified as spring-loaded hinges, simultaneously driven by a tendon like flexor digitorum profundus. The joint spring is the mechanical equivalent to all other soft tissues, such as metacarpophalangeal dorsal expansion of finger and extensor digitorum. A series of frictionless fixed attachment points regulate the tendon path, which mimics the function of superficialis, synovial tendon sheaths, and annular pulley. The behavior of the da Vinci's mechanism depends on the location of attachment points and the joint spring stiffness. The tendon lengthc, i.‍e. the summation of distance between neighboring attachment points, is a function of MCP, PIP, and DIP joint angles (mcp,pip, anddip):

Fig. 1 Comparison between the anatomy of a finger (left) and the da Vinci's mechanism (right)

where=[mcp,pip,dip]T,=diag(mcp,pip,dip) is a weight matrix,wcorresponds to the stiffness of each joint, and=∂c/∂is the Jacobian matrix. Eq. (2) represents the relation between joint displacement and tendon contraction length.

2.2 Bionic optimization of da Vinci’s mechanism

The coupling among DIP, PIP, and MCP joint angles reveals that the motion of a robot hand finger is natural. To reproduce the postural synergic characteristic of the human hand, the undetermined parameter of da Vinci's mechanism is optimized according to the dataset of daily hand gestures of a human being (Santello et al., 1998). Linear principal component analysis (PCA) is used to find this coupling relation between joints, as shown in Fig. 2. The importance of the coupling is characterized by the parameterc, defined as

whereΛis the corresponding eigenvalue of theth component of the PCA. Largercmeans the human digit is more inclined to move in this direction. The first component contribution rate is in the range of 60%–75% for different fingers of a human hand. The results suggest that more than 60% of a finger's motion in daily living can be captured by using one generalized DOF. Especially for the middle, ring, and little fingers, which are mainly responsible for the power grasping function of the hand, the first component contribution rate is over 70%.

Fig. 2 Contribution rates of the three principal components from the PCA of the dataset of human daily hand gestures

Fig. 3 visualizes the joint angles of the ring finger in the dataset of human daily hand gestures in the coordinate systems of (mcp,pip) (left chart) and (mcp,dip) (right chart). The densely overlapped data points show the greatest probability of the coupling relation, which is described by the first component direction of the linear PCA:

where the coefficientspip,dip,pip, anddipare calculated by linear fitting of the angles of the joints. The optimized results are also plotted in Fig. 3 for comparison. The optimized design can almost realize the ideal linear coupling among DIP, PIP, and MCP joints, even though the da Vinci's mechanism is kinematically nonlinear.

Fig. 3 Visualization of the coupling relation: MCP and PIP joints of the ring finger (left); MCP and DIP joints of the ring finger (right). The straight red lines indicate the most probable direction according to PCA. The blue curves are the coupling relations of the optimized da Vinci's mechanism. The scatter shows the dataset of the hand. Yellow indicates high density while lilac indicates low density. References to color refer to the online version of this figure

2.3 Twisted string actuation mechanism

The twisted string actuation (TSA) mechanism converts rotational movement of the electronic motor to translation by twisting a single or a bunch of strings, as shown in Fig. 4. Compared with other transmission mechanisms, such as linkage and lead screw, TSA is more flexible and compact. This feature is especially beneficial for an anthropomorphic robot hand with extremely limited space. Eq. (6) gives the relation between the contraction lengthand the twist angle:

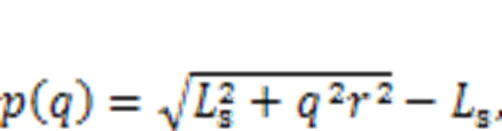
where Ls is the length of the twist region and r the radius of a string.

To avoid over twist and unwinding problems of TSA, a maximum rotation anglemaxshould be imposed as a geometry constraint,max=πs/(2). Takingmaxinto Eq. (6), one can get the maximum contraction lengthmax≈0.86s. Ignoring friction, the contraction force can be derived from Eq. (6) by the law of energy conservation:

whererepresents the output torque of the motor. The above equation reveals a nonlinear transmission ratio of TSA with a singularity at=0. Given a constant torque output of the motor, the contraction force will decrease with the twist angle. The string radius is a key design parameter in Eq. (7). A larger string radius will lower the transmission ratio and lead to a higher speed, given a specific twist angle and constant rotation speed of the motor.

3 Results and discussion

3.1 Implementation and test of bionic robot finger

Fig. 5a shows the assembled 3D printed finger. The attachment point is realized as a shaft with a tubular polytetrafluoroethylene (PTFE) sheath. High-strength and smooth polyethylene fiber (Dyneema) is used as both the tendon and the strings. The friction effect on the mechanical behavior is further minimized by coating the Dyneema fiber with grease. A splitter is located between the MCP and PIP joints. Fig. 5b shows the experimental results of a ring finger fabricated according to the optimized da Vinci's mechanism. The slope and bias of the fitting lines are close to the optimized design. A slight deviation from the ideal line may be caused by the unavoidable friction of the transmission system. In addition, although the joints of the digit are designed to be a linear coupling relationship, the under-actuated property of the mechanism allows the digit to adapt to different objects.

Fig. 5 Implement of optimized da Vinci's mechanism robot finger: (a) the assembled 3D printed finger based on the optimized da Vinci's mechanism and TSA; (b) linear fit between PIP, DIP, and MCP joints according to three kinematics tests. The sub-image shows the trajectory of the robot finger

The finger performance has been evaluated for both speed (Fig. 6) and force outputs (Fig. 7). The sub-image of Fig. 6 is the setup for testing grasp velocity, which is defined as the MCP joint angle velocity (Belter et al., 2013). In the current setup, the MCP joint rotates for 70° before the fingertip can touch the topside button, which triggers a stop signal to the electric motor. In this way, the actuation duration is accurately measured for the grasp velocity calculation. As the string diameter of TSA changes from 0.4 to 1.0 mm, the grasp velocity varies from 107 to 233 (°)/s at 18 V. This performance is comparable to that of the human hand (172 to 200 (°)/s) for daily pick-and-place tasks (Belter et al., 2013).

Fig. 6 Experimental measurements of the maximum grasp speed under different voltages and diameters of the string. Each set of experiments was performed three times, and error bars represent three standard deviations

Fig. 7 Experimental measurements of the fingertip force under different currents and diameters of the string. Error band represent three standard deviations

The fingertip force output is measured by a calibrated cantilever beam, as shown in the sub-image of Fig. 7. The force output depends on both the driven current of the electric motor and the string diameters as Eq. (7) shows. The current threshold presents in all TSA with different string diameters, revealing the non-negligible friction from the 20:1 gear set integrated in the electric motor. Above the threshold, the force is linearly proportional to the driven current. The maximum forces, achieved at the driven current of 0.55 A, are 6.4, 8.3, and 14.7 N for string diameters of 1.0, 0.6, and 0.4 mm, respectively. To balance both the grasp velocity and the maximum fingertip force, we choose the string with a diameter of 0.6 mm in the TSA for the robot hand. The maximum fingertip force (8.3 N) is about 54% of human-level performance and the fastest grasp velocity (142 (°)/s) is about 83% of human-level performance.

3.2 System of an anthropomorphic hand

Fig. 8a shows the 3D layout of a human-size anthropomorphic robot hand, based on the da Vinci's mechanism and TSA. The detailed setup of the ring finger, as an example, is shown in the upper inset to Fig. 8a. Fig. 8b shows the assembled robot hand. The DIP, PIP, and MCP joints are designed as the bearing-supported hinge structure to reduce the friction force during rotation. The electric motor, integrated with gear sets and magnetic encoders, has a rated speed of 2200 r/min at 12 V with an installed 20:‍1 gear set. The thumb takes over 40% of the functions of the human hand (Xiong et al., 2016). A dexterous and powerful thumb is essential for the robot hand to achieve the human-level performance of grasp. The design of the thumb has extra complexity. In the current design, only the interphalangeal (IP) and metacarpophalangeal (MP) joints are driven by TSA, while the carpo-metacarpal (CMC) joint is directly actuated by a 150:‍1 gear motor (the rated rotation speed is 143 r/min at 12 V). Motors are driven by the customized printed circuit board with six channel H-bridges (three DRV8848 motor drivers) and one programmed chip (STM32F405). A position feedback controller is used to control the contraction length of tendons. All other structural components, except attachment point shafts, joint springs, and bearings, are 3D-printed using light curing resin. The anthropomorphic robot hand has six active DOFs and 15 passive DOFs. The length, width, and thickness are 205, 94, and 29 mm, respectively, close to an adult hand. The total weight is 280 g without battery.

Fig. 8 3D model and realization of the robot hand: (a) layout of the 3D design showing the integration of the da Vinci's mechanism and TSA in the robot hand; (b) assembled robot hand based on the design in (a).The boxed regions with blue dashed lines highlight the locations of six electric motors. The red dotted lines and rotation arrows show all the passive DOFs. The integration of the motor in the thumb is shown in the lower inset to (a). The upper inset reveals the TSA mechanism in the middle finger. The symbol "ab/ad" represents the abduction/adduction degree of freedom. References to color refer to the online version of this figure

3.3 Dexterity and adaptability

To demonstrate dexterity and mechanical adaptability, grasping experiments have been performed using the anthropomorphic robot hand according to the taxonomy of Feix et al. (2016) (Movie S1 in the electronic supplementary materials (ESM)), which summarizes the most frequently used gestures in daily life. All grasp tests last at least 3 s to ensure a stable grip. The results, as categorized in Fig. 9, show that the robot hand can reproduce 30 of the 33 types of gesture. This is expected since the employed da Vinci's mechanism has been well optimized using the hand gesture data collected from daily living. The trajectory of the digit follows the direction of the highest probability of hand gesture. Moreover, it shows good adaptability in the grasping experiments. This is deeply rooted in the design of the under-actuated rigid-flexible hybrid system, which has 15 passive DOFs in total, allowing free adaptation to objects over a large range. Three of the 33 types of taxonomy test failed. They involved gestures like gripping scissors, chopsticks or a pen (boxed with dashed line in Fig. 9). All the three gestures are characterized by the abduction and adduction motions of the digits, which is lacking in our current design.

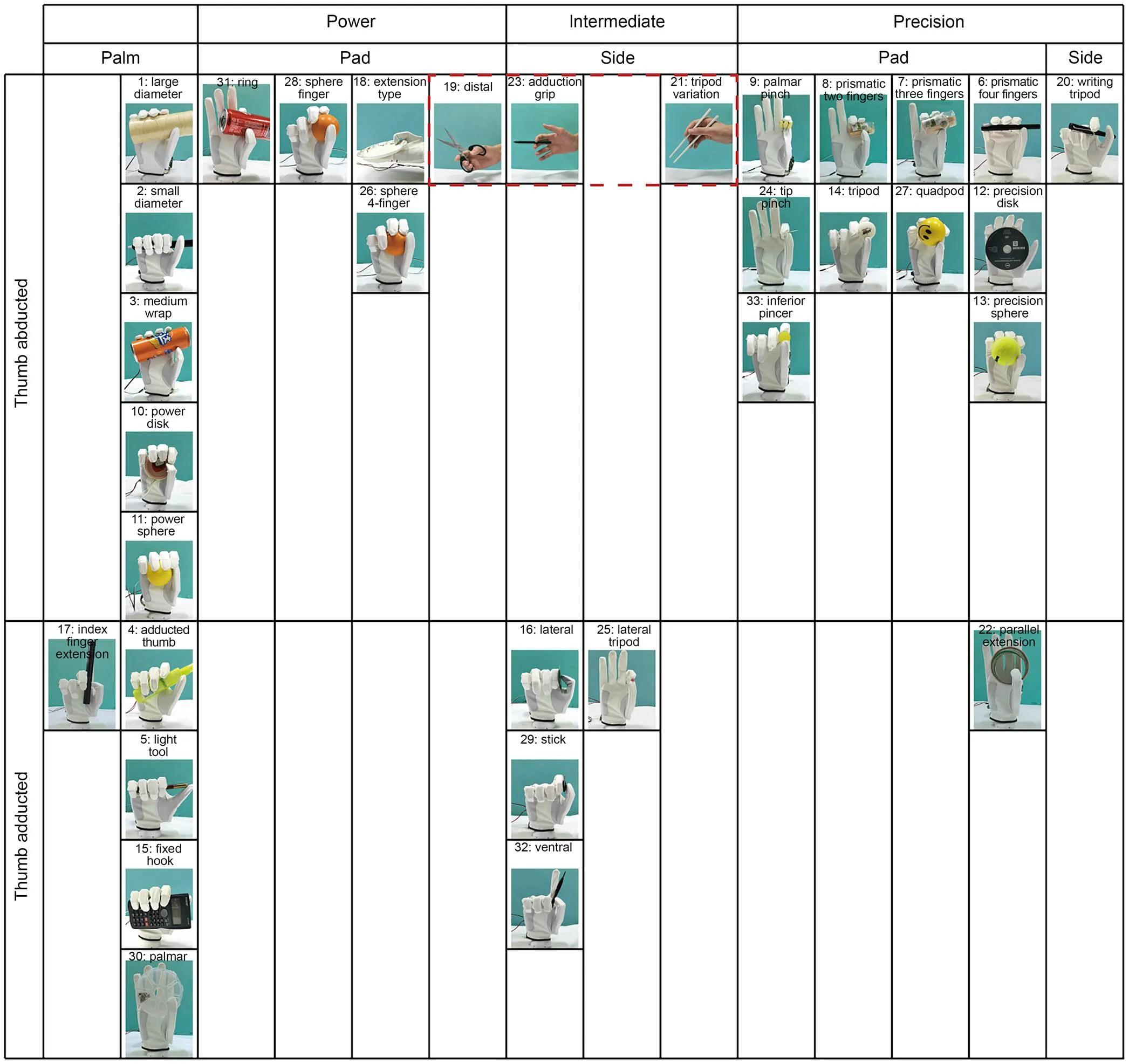
Fig. 9 Anthropomorphic grasping tests according to the taxonomy of Feix et al. (2016). Thirty of the 33 gestures are demonstrated in this work and 3 of the 33 gestures (indicated by the dashed-line box) are unable to be realized. The objects for grasp tests are common in daily life

The adaptability of the robot hand is further quantified using the physical simulator MuJoCo (Todorov et al., 2012), which can accurately solve the tendon system and the contact problem. The physical model is built on the optimized da Vinci's mechanism and accurately captures the motion of the real robot hand in simulation. Without loss of generality, power grasp of cylinders and cuboids with various dimensions has been studied. In simulations, all five tendons of the robot hand model have had the same force of 20 N applied. Given the above condition, the contact area and the pressure are solely determined by the adaptability of the robot hand. The overall performance can thus be compared using the maximal sliding force that pulls out the object from the side.

For cylinder tests, the sliding force is applied along the axial direction. The maximal loads remain nearly constant (about 55 N) for diameters ranging from 10 to 40 mm and decrease for diameters larger than 50 mm (Fig. 10). For cuboid tests, the dimensions of the cross-section are limited by the grasp capacity of the robot hand. The shape is roughly described by the aspect ratio/(andrepresent the length and width of the rectangular section, respectively). The maximal sliding force is in the range of 52 to 55 N with/varying from 0.25 to 4.00. It is interesting to note that this value is close to that in the cylinder tests. Such consistency indicates the good adaptability of the da Vinci's mechanism.

3.4 Power grip test

Power grasp is another important requirement for anthropomorphic robot hands. The performance is determined by the power of the actuation system, the strength of the mechanical structure, and the interaction between the hand and the object. To minimize the effect of interfacial slip, the handle of the weight is covered with 5 mm-thick sponge and the robot hand wears a golf glove. The handle is grasped in the vertical position. A maximal weight of 5 kg can be lifted without damaging the robot hand (Fig. 11).

Fig. 10 Maximal pulling forces versus the size and the shape of the objects. The inset shows the grasp of cylinders with different diameters d and cuboids with different cross-sections. The shape of the cuboid cross-section is given by the aspect ratio a/b. The histogram gives the corresponding maximal load that can pull the object out of the hand along the axial direction. Error bar represents three standard deviations

3.5 Application demonstration

The fusion of optimized da Vinci's mechanism and TSA coordinates the dexterity, power, and compactness of the anthropomorphic robot hand. Those features provide the potential for a robot hand to work in human living scenarios. Fig. 12 shows the application of robot hand in China's first clinical translational study of an implantable brain-computer interface (BCI). A robot hand is fixed on a Kinova robot arm and is mainly responsible for the grasping task. Good adaptability reduces the requirement for precision of the robot hand and arm, which is especially difficult for both the patient and BCI controller algorithm.

For applications in the field of anthropomorphic prosthetics, the most important properties include weight, size, fingertip force, grasp velocity, and active and passive dexterity. Fig. 13 compares our robot hand and the commercially available robot hands with the human hand using radar charts. All six properties are normalized to the corresponding value of the human hand. Qualitatively, the area of the polygon spanned by the properties reveals the overall performance. As compared to the commercial prosthetic hands, our robot hand based on the optimized da Vinci's mechanism and TSA has made improvements in comprehensive performance. The most prominent feature of the current design is that the fingertip force and the grasp velocity performance are approaching the performance of the human hand, while retaining light weight and compactness. The better performance of the human hand in both the force output and the grasp velocity is due to an intelligent sensor-free and autonomous force-velocity adaptation mechanism. In the human hand, the tendon sheath (Xu and Todorov, 2016) can undergo a large elastic deformation. High grasp velocity can be easily achieved when the tendon glides freely in the sheath attached closely to the phalanx. When the large grasp force is required, the sheath deforms elastically and the attachment point will move far away from the phalanx, resulting in a larger moment arm. Such a sensor-free and self-adaptive natural mechanism gives both speed and power to the human hand. In recent studies (Shin et al., 2012; Jeong et al., 2017), a dual-mode TSA scheme has been proposed to achieve adaptive output of force and speed. In the future, carefully designed elastic structures with proper load-deformation behavior will be integrated into the TSA in cooperation with the da Vinci's mechanism. We expect the overall performance will be further improved towards that of the human hand.

Fig. 11 Power grasp tests of the robot hand. The rod weights 0.5 kg, and has a sponge wrap at the top. Each counterpoise weight is 1.5 kg

Fig. 12 Application of anthropomorphic robot hand in China's first clinical translational study of the implantable brain-computer interface for motor function reconstruction

Fig. 13 Comprehensive performance of commercial prosthetics and this work. Six key properties for prosthetics, including ligntness (L), compactness (C), fingertip force (F), grasp velocity (V), active (DA), and passive dexterity (DP), are normalized by the human hand performance. The data (Table S1 in the ESM) for the commercial prosthetics, i.‍e. iLimb, BeBionic, and Vincent, are from published resources (Belter et al., 2013; Vincent, 2022). The vertices of the regular hexagon have the unit value, which come from the human hand reference (Yokogawa and Hara, 2002; Cobos et al., 2010; Belter et al., 2013)

4 Conclusions

In summary, we present a novel design based on the under-actuated da Vinci's mechanism driven by TSA. The tendon-driven scheme allows structural optimization using a motion capture database to reproduce the natural movement of the human hand. The under-actuated robot hand with 15 passive DOFs shows excellent adaptation to free-form objects. The application of TSA realizes high conversion from the motor torque to the tendon contraction force while keeping the structure light, flexible, and compact. Our anthropomorphic prosthetic hand, consisting of six active DOFs, has a weight of 280 g, approximately 70% of that of a human hand. It has passed through 30 of the 33 grasp tests on daily living objects according to Feix et al. (2016)'s taxonomy and retains a loading capacity of 5 kg at the same time. The simple and intelligent mechanism leads to excellent stability and adaptability, making feasible a wide range of applications in prosthetics and service robots.

This work is supported partly by the Fund of State Key Laboratory of Fluid Power and Mechatronic Systems (Zhejiang University), China.

Hong-tao WANG and Wei YANG designed the research. Yong-bin JIN performed the experiments and fabricated the robot. Shao-wen CHENG did the simulation of robot hand. Yan-yan YUAN applied the robot hand to the brain-computer interface experiments. Yong-bin JIN wrote the first draft of the manuscript. Yong-bin JIN, Hong-tao WANG, and Wei YANG revised and edited the final version.

Yong-bin JIN, Shao-wen CHENG, Yan-yan YUAN, Hong-tao WANG, and Wei YANG declare that they have no conflict of interest.

Andrianesis K, Tzes A, 2013. Design of an innovative prosthetic hand with compact shape memory alloy actuators. Proceedings of the 21st Mediterranean Conference on Control and Automation, p.697-702. https://doi.org/10.1109/MED.2013.6608799

Andrychowicz M, Baker B, Chociej M, et al., 2020. Learning dexterous in-hand manipulation., 39(1):3-20. https://doi.org/10.1177/0278364919887447

Belter JT, Segil JL, Dollar AM, et al., 2013. Mechanical design and performance specifications of anthropomorphic prosthetic hands: a review., 50(5):599-618. https://doi.org/10.1682/JRRD.2011.10.0188

Billard A, Kragic D, 2019. Trends and challenges in robot manipulation., 364(6446):eaat8414. https://doi.org/10.1126/science.aat8414

Brown E, Rodenberg N, Amend J, et al., 2010. Universal robotic gripper based on the jamming of granular material., 107(44):18809-18814. https://doi.org/10.1073/pnas.1003250107

Chen C, Zou J, 2021. Adaptive robust control of soft bending actuators: an empirical nonlinear model-based approach., 22(9):681-694. https://doi.org/10.1631/jzus.A2100076

Cobos S, Ferre M, Sánchez-Urán MÁ, et al., 2010. Human hand descriptions and gesture recognition for object manipulation., 13(3):305-317. https://doi.org/10.1080/10255840903208171

de Pascali C, Naselli GA, Palagi S, et al., 2022. 3D-printed biomimetic artificial muscles using soft actuators that contract and elongate., 7(68):eabn4155. https://doi.org/10.1126/scirobotics.abn4155

Deimel R, Brock O, 2016. A novel type of compliant and underactuated robotic hand for dexterous grasping., 35(1-3):161-185. https://doi.org/10.1177/0278364915592961

Feix T, Romero J, Schmiedmayer HB, et al., 2016. The GRASP taxonomy of human grasp types., 46(1):66-77. https://doi.org/10.1109/THMS.2015.2470657

Firouzeh A, Paik J, 2017. Grasp mode and compliance control of an underactuated origami gripper using adjustable stiffness joints., 22(5):2165-2173. https://doi.org/10.1109/TMECH.2017.2732827

Galloway KC, Becker KP, Phillips B, et al., 2016. Soft robotic grippers for biological sampling on deep reefs., 3(1):23-33. https://doi.org/10.1089/soro.2015.0019

Gaponov I, Popov D, Ryu JH, 2014. Twisted string actuation systems: a study of the mathematical model and a comparison of twisted strings., 19(4):1331-1342. https://doi.org/10.1109/TMECH.2013.2280964

Grebenstein M, Chalon M, Hirzinger G, et al., 2010. Antagonistically driven finger design for the anthropomorphic DLR hand arm system. Proceedings of the 10th IEEE-RAS International Conference on Humanoid Robots, p.609-616. https://doi.org/10.1109/ICHR.2010.5686342

Jeong SH, Kim KS, Kim S, 2017. Designing anthropomorphic robot hand with active dual-mode twisted string actuation mechanism and tiny tension sensors., 2(3):1571-1578. https://doi.org/10.1109/LRA.2017.2647800

Jung MY, Chuc NH, Kim JW, et al., 2006. Fabrication and characterization of linear motion dielectric elastomer actuators. Proceedings of SPIE 6168, Smart Structures and Materials 2006: Electroactive Polymer Actuators and Devices, Article 616824. https://doi.org/10.1117/12.658145

Kim U, Jung D, Jeong H, et al., 2021. Integrated linkage-driven dexterous anthropomorphic robotic hand., 12(1):7177. https://doi.org/10.1038/s41467-021-27261-0

Laffranchi M, Boccardo N, Traverso S, et al., 2020. The Hannes hand prosthesis replicates the key biological properties of the human hand., 5(46): eabb0467. https://doi.org/10.1126/SCIROBOTICS.ABB0467

Lee DH, Park JH, Park SW, et al., 2017. KITECH-hand: a highly dexterous and modularized robotic hand., 22(2):876-887. https://doi.org/10.1109/TMECH.2016.2634602

Li SG, Stampfli JJ, Xu HJ, et al., 2019. A vacuum-driven origami “magic-ball” soft gripper. Proceedings of the International Conference on Robotics and Automation, p.7401-7408. https://doi.org/10.1109/ICRA.2019.8794068

Liu H, Meusel P, Hirzinger G, et al., 2008. The modular multisensory DLR-HIT-Hand: hardware and software architecture., 13(4):461-469. https://doi.org/10.1109/TMECH.2008.2000826

Liu MJ, Xiong CH, Xiong L, et al., 2016. Biomechanical characteristics of hand coordination in grasping activities of daily living., 11(1):e0146193. https://doi.org/10.1371/journal.pone.0146193

Liu XH, Zheng XH, Li SP, 2017. Development of a humanoid robot hand with coupling four-bar linkage., 9(1):1-13. https://doi.org/10.1177/1687814016686313

Liu XW, Jin YB, Jiang L, et al., 2021. Wheeled jumping robot by power modulation using twisted string lever mechanism., 22(10):767-776. https://doi.org/10.1631/jzus.A2000618

Mahler J, Liang J, Niyaz S, et al., 2017. Dex-Net 2.0: deep learning to plan robust grasps with synthetic point clouds and analytic grasp metrics. Proceedings of the Robotics: Science and Systems XIII.

O’Brien KW, Xu PA, Levine DJ, et al., 2018. Elastomeric passive transmission for autonomous force-velocity adaptation applied to 3D-printed prosthetics., 3(23):eaau5543. https://doi.org/10.1126/scirobotics.aau5543

Oh S, Tabassian R, Thangasamy P, et al., 2022. Cooling-accelerated nanowire-nitinol hybrid muscle for versatile prosthetic hand and biomimetic retractable claw., 32(18):2111145. https://doi.org/10.1002/adfm.202111145

Palli G, Natale C, May C, et al., 2013. Modeling and control of the twisted string actuation system., 18(2):664-673. https://doi.org/10.1109/TMECH.2011.2181855

Rajeswaran A, Kumar V, Gupta A, et al., 2018. Learning complex dexterous manipulation with deep reinforcement learning and demonstrations. Proceedings of the Robotics: Science and Systems XIV.

Ruotolo W, Brouwer D, Cutkosky MR, 2021. From grasping to manipulation with gecko-inspired adhesives on a multifinger gripper., 6(61):eabi9773. https://doi.org/10.1126/scirobotics.abi9773

Santello M, Flanders M, Soechting JF, 1998. Postural hand synergies for tool use., 18(23): 10105-10115. https://doi.org/10.1523/jneurosci.18-23-10105.1998

Schmitz A, Pattacini U, Nori F, et al., 2010. Design, realization and sensorization of the dexterous iCub hand. The 10th IEEE-RAS International Conference on Humanoid Robots, p.186-191. https://doi.org/10.1109/ICHR.2010.5686825

Shin YJ, Lee HJ, Kim KS, et al., 2012. A robot finger design using a dual-mode twisting mechanism to achieve high-speed motion and large grasping force., 28(6):1398-1405. https://doi.org/10.1109/TRO.2012.2206870

Shintake J, Cacucciolo V, Floreano D, et al., 2018. Soft robotic grippers., 30(29):1707035. https://doi.org/10.1002/adma.201707035

Shorthose O, Albini A, He L, et al., 2022. Design of a 3D-printed soft robotic hand with integrated distributed tactile sensing., 7(2):3945-3952. https://doi.org/10.1109/LRA.2022.3149037

Todorov E, Erez T, Tassa Y, 2012. MuJoCo: a physics engine for model-based control. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, p.5026-5033. https://doi.org/10.1109/IROS.2012.6386109

Vincent, 2022. Vincent Prosthetics Hand. https://www.vincentsystems.de/vincent-evolution4

Weiss EJ, Flanders M, 2004. Muscular and postural synergies of the human hand., 92(1): 523-535. https://doi.org/10.1152/jn.01265.2003

Xiong CH, Chen WR, Sun BY, et al., 2016. Design and implementation of an anthropomorphic hand for replicating human grasping functions., 32(3):652-671. https://doi.org/10.1109/TRO.2016.2558193

Xu K, Liu H, Du YH, et al., 2014. Design of an underactuated anthropomorphic hand with mechanically implemented postural synergies., 28(21):1459-1474. https://doi.org/10.1080/01691864.2014.958534

Xu Z, Todorov E, 2016. Design of a highly biomimetic anthropomorphic robotic hand towards artificial limb regeneration. Proceedings of the IEEE International Conference on Robotics and Automation, p.3485-3492. https://doi.org/10.1109/ICRA.2016.7487528

Yang Y, Jin KX, Zhu HH, et al., 2021. A 3D-printed fin ray effect inspired soft robotic gripper with force feedback., 12(10):1141. https://doi.org/10.3390/mi12101141

Yang ZS, Yin KK, Liu LB, 2022. Learning to use chopsticks in diverse gripping styles., 41(4):95. https://doi.org/10.1145/3528223.3530057

Yip MC, Niemeyer G, 2015. High-performance robotic muscles from conductive nylon sewing thread. Proceedings of the IEEE International Conference on Robotics and Automation, p.2313-2318. https://doi.org/10.1109/ICRA.2015.7139506

Yokogawa R, Hara K, 2002. Measurement of distribution of maximum index-fingertip force in all directions at fingertip in flexion/extension plane., 124(3):302-307. https://doi.org/10.1115/1.1468637

Zhao HC, O’Brien K, Li S, et al., 2016. Optoelectronically innervated soft prosthetic hand via stretchable optical waveguides., 1(1):eaai7529. https://doi.org/10.1126/scirobotics.aai7529

Movie S1 and Table S1

Apr. 18, 2022;

Revision accepted Aug. 8, 2022;

Crosschecked Sept. 15, 2022

© Zhejiang University Press 2022