永磁同步电机双环模型预测控制研究

胡文浩，尹 强，孙 乐，刘国栋

(1.南京理工大学 机械工程学院，南京 210094；2.南京理工大学 自动化学院，南京 210094；3.北方自动控制技术研究所，太原 030006)

0 引 言

永磁同步电机(以下简称PMSM)因具有结构简单、运行可靠、体积小、效率高等优点，在工业领域中得到了广泛的应用。电机控制策略直接影响着控制效果。目前应用的控制策略有矢量控制、直接转矩控制和恒压频比控制[1]。前两种控制策略应用更广泛，也更成熟。为了满足实际应用中的控制需求，在目前控制策略的基础上，衍生出了各种现代控制策略，如滑模控制、模型预测控制(以下简称MPC)、自适应控制、神经网络控制、无传感器控制等。其中，MPC控制结构简单、动态响应速度快，引起了广泛关注，已成为PMSM控制领域的热点研究方向。

根据控制集的连续性，MPC可分为连续控制集模型预测控制(以下简称CCS-MPC)和有限控制集模型预测控制(以下简称FCS-MPC)。而根据控制对象的不同，MPC又可分为模型预测电流控制(以下简称MPCC)和模型预测转矩控制[2]。

FCS-MPCC利用离散的电机数学模型进行预测和分析计算，从而得到未来时刻的电流值，再通过成本函数评估选出最优电压矢量。文献[3]提出了一种基于时间尺度自适应调整的MPCC算法，以提高PMSM在暂态过程的动态响应和预测精度，同时减小了计算量，提高了稳态时的控制性能。该文分析了多时间尺度MPCC算法中信号采样、预测计算、控制输出、模型误差修正等不同部分的时间尺度特性，提出了多时间尺度MPCC算法体系结构。针对MPCC在开式绕组PMSM驱动系统中面临的枚举过程和多目标成本函数评估的复杂性挑战，文献[4]提出了一种低复杂度的MPCC算法，消除了在线枚举过程和代价函数的评估。该算法根据预先设定的优化准则，从控制集中选择与参考矢量匹配的最优电压矢量。文献[5]提出了一种有效的双矢量MPCC，即在一个控制周期内任意施加2个电压矢量，首先根据无差拍电流控制原理计算出基准电压矢量，在此基础上，可以快速得到2个最优矢量及其持续时间。

针对非线性PMSM转速控制系统中控制器输出饱和的问题，文献[6]提出了一种新型的抗饱和模型预测控制方法。将非线性PMSM转速控制系统转化为时变线性系统，将系统变量的阈值转化为系统约束条件，设计线性模型预测控制器实现对系统的抗饱和控制。同时，引入椭圆不变集来保证FCS-MPC系统的稳定性。文献[7]提出一种双模型MPC对PMSM的速度和电流进行控制，速度外环采用模型预测控制器，电流内环采用无差拍预测控制器，但是该文没有考虑到参数不确定性等因素造成的误差。扩展状态观测器(以下简称ESO)可以对系统的扰动进行观测并补偿，抑制了不确定扰动对控制产生的影响。文献[8-11]采用ESO对控制系统进行补偿。

本文以PMSM控制的摇臂装置为研究对象。在MPCC的基础上，提出了一种改进型模型预测电流控制(以下简称SS-MPCC)，在预先选择扇区、缩小候选矢量范围的基础上选择出最优电压矢量。与此同时，控制外环即速度环也采用MPC代替PI控制，降低了控制系统的复杂性，在速度环MPC中设计使用了二阶ESO以补偿扰动，使得速度控制更加高效精准，提高了系统整体的动态响应性能。

1 MPCC

1.1 控制对象

本文以PMSM控制的摇臂装置为研究对象，如图1所示。

图1 电机及其摇臂装置

1.2 PMSM的数学模型

在同步旋转坐标系下，电机定子电压方程：

(1)

式中：Rs为定子电阻；ud,uq分别为d-q轴的定子电压分量；id，iq分别为d-q轴的定子电流分量；Ld，Lq为d-q轴电感；ωele为转子的电角速度；ψf为永磁体磁链。

1.3 MPCC

以电流为状态变量，可将式 (1)转化如下：

(2)

利用一阶向前欧拉法将式 (2)离散化：

(3)

式中：Ts为电流环的采样周期。

MPC可以考虑多个控制目标作为变量加入到成本函数中。本文MPCC算法的控制目标是电流，要求令定子的d，q轴电流分量跟随其参考给定值。构建如下成本函数：

(4)

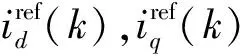
对两电平三相逆变器而言，一共有8种开关组合状态，其中存在2个零矢量V0与V7，故电压矢量数为7。将上述7种电压矢量对应计算出的电流预测值代入式 (4)，分别计算出各电压矢量相对应的成本函数值并进行比较，成本函数值为最小所对应的电压矢量即为最优电压矢量，以该电压矢量控制三相逆变器。

当选择出的最优电压矢量为零矢量时，根据开关切换频率最低的原则，确定V0或V7。若上一时刻确定的电压矢量为V0，V1，V2，V4，则当前时刻选择V0为最优电压矢量，反之选择V7。

1.4 SS-MPCC

MPCC需要预测7次电流并计算相对应的成本函数值，计算量庞大，计算时间长，对处理器的性能要求较高。本文在传统MPCC的基础上，提出了一种基于先择扇区原则的SS-MPCC算法。

将式 (1)离散化：

(5)

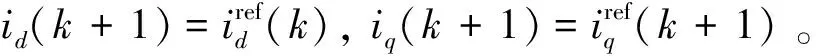
(6)

可得到k时刻的d，q轴定子电压参考值，进而可得参考电压在同步旋转坐标系下的角度：

(7)

(8)

计算出参考电压在静止坐标系下的角度后，可以得到其所在扇区，如图2所示。

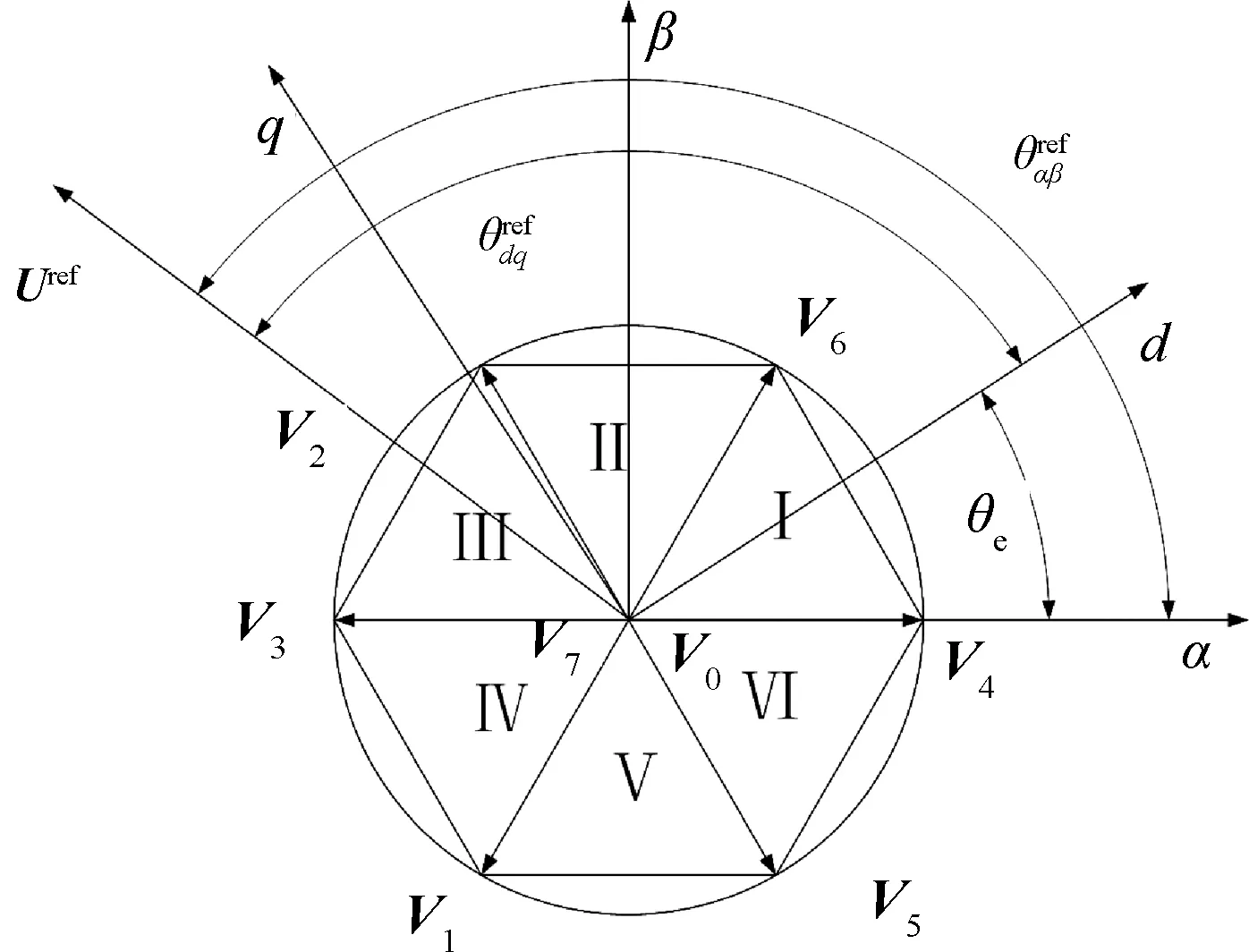
图2 预测参考电压所在扇区

选择构成该参考电压矢量所在扇区的2个矢量及零矢量作为候选矢量， 代入式 (3)、 式(4)计算比较，并得到最优电压矢量。例如在图2中，参考电压矢量处于扇区Ⅲ，候选矢量为V0(V7)，V2，V3，零矢量的选择与上节所述相同。与MPCC的7次预测相比，SS-MPCC只需要预测3次，很大程度上减小了计算量。

若计算出的参考电压矢量恰好与某矢量重合，由于系统误差的存在，将该矢量相邻的2个矢量和零矢量纳入考虑范围，以上述三者及零矢量作为候选矢量。此种情况下，SS-MPCC的计算量同样比MPCC所需的计算量小。

2 速度环控制器设计

2.1 速度环MPC

PMSM的机械运动方程：

(9)

式中：ωm是机械角速度；J是转动惯量；Te是电机的输出转矩；TL是负载转矩；C是阻尼系数。

将式 (9)离散化，同时因为C较小，忽略阻尼项，得:

(10)

速度预测参考轨迹如下：

(11)

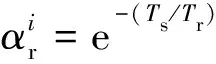
为使计算过程更加简便，将k时刻的实际速度ω(k)与预测速度ωm(k)的差值设定为常数误差eω(k) =ω(k)-ωm(k)，则在k时刻的第i步预测下，速度参考值ω*(k+i)与实际速度值ω(k+i)的差值如下：

ω*(k+i)-ω(k+i)=ω*(k+i)-

ωm(k+i)-eω(k+i)

(12)

基于上述，建立成本函数，即:

(13)

式中：rm为权重系数。

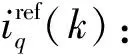
(14)

式中：D是搜索域。

2.2 ESO设计

速度环控制器中的二阶ESO可以补偿各项扰动造成的系统误差。设计如下：

(15)

式中：z1=ω；h= (Te-TL)/J；m(t)是考虑了各项扰动的总扰动集合。建立二阶ESO：

(16)

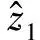
速度控制器原理如图3所示。

图3 速度控制器原理图

3 总控制器设计

本文采用双环MPC算法，外环速度环用MPC代替传统的PI控制，同时使用了ESO对包含参数不确定性在内的误差进行补偿。

内环电流环则采用SS-MPCC，以先选择候选扇区的方式减少了候选电压矢量数。

完整的电机控制摇臂装置系统如图4所示。

图4 摇臂装置控制系统图

4 仿真研究

为了验证本文算法的性能，利用MATLAB/Simulink搭建对应摇臂装置控制系统，仿真比较双环PI和双环MPC的控制效果。仿真使用的PMSM参数：额定输出功率为750 W，额定输出转矩为3.36 N·m，额定转速为3 000 r/min，额定电流为5 A，电源电压为150 V(DC)，瞬时最大转矩为10.08 N·m，瞬时最大电流为15 A，电机永磁磁链为0.112 Wb，转子转动惯量为1.2 kg·cm2。负载摇臂从0°运动到90°，到位误差要求为0.02°,其中，当摇臂竖直向下时，角度定为0°。

本文的仿真与实验部分研究比较了双环PI控制与双环MPC，通过控制摇臂装置的运动，对到位精度与所需时间进行比较，验证双环MPC算法的快速动态响应性。为消除不必要的干扰，在下述仿真和实验中，两种算法的位置环参数完全一致。

位置环指令输出并不是直接给定一个数值，而是通过速度规划的方法给出。

4.1 PI仿真

图5是速度环和电流环都采用PI控制得到的仿真数据曲线。其中，速度环Kp=12，Ki=120；电流环Kp=20，Ki=400。在该算法下，达到所要求的角度精度所用时间为1.65 s，最终收敛于指令角度，但收敛速度较慢。

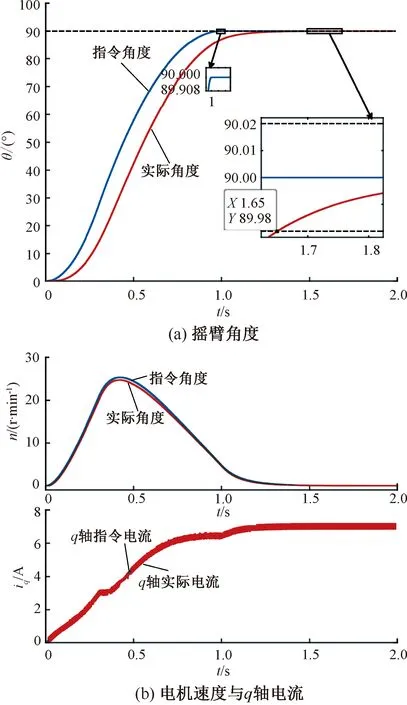
图5 双环PI算法仿真结果图

4.2 MPC仿真

图6是双环MPC算法所得到的对应仿真数据曲线。采用该算法，到达所要求的角度精度，用时只需1.469 s，比PI算法用时少0.181 s。对比图5、图6可观察到，双环MPC算法收敛速度更快。在双环MPC算法下，1.8 s时摇臂实际角度近乎达到90°，而在PI算法下，1.9 s时摇臂实际角度与90°还有一定误差。

图6 双环MPC算法仿真结果图

从图6(b)可以看出，MPC算法比PI算法所产生的电流振荡要大，这是因为MPC减小了逆变器的开关频率。PI算法中的电流环采用空间矢量脉宽调制算法，在一个控制周期内需要切换6次逆变器开关，对逆变器的损耗较大。而采用MPC算法，在一个控制周期内至多只需要切换一次开关，可使得逆变器使用寿命增长。

5 实验验证

本文不仅做了仿真验证，而且也搭建了相对应的实验平台，具体如图 7所示。

图7 电机控制实验平台

此实验平台主要由PMSM及其负载摇臂、直流电源、上位机、驱动器、烧录器和数据采集仪构成。实验所用PMSM的参数与仿真相同。驱动器是基于数字信号处理器设计的，受控输出终端为两电平三相逆变器。数据采集仪为周立功ZLG-CAN分析仪，实验所需要的数据采集至数据采集计算机上保存。

5.1 双环PI实验分析

图8是速度环和电流环都采用PI进行控制得到的对应实验数据曲线。其中，设置速度环Kp=12，Ki=120，与仿真参数设置相同；设置电流环Kp=3，Ki=400。

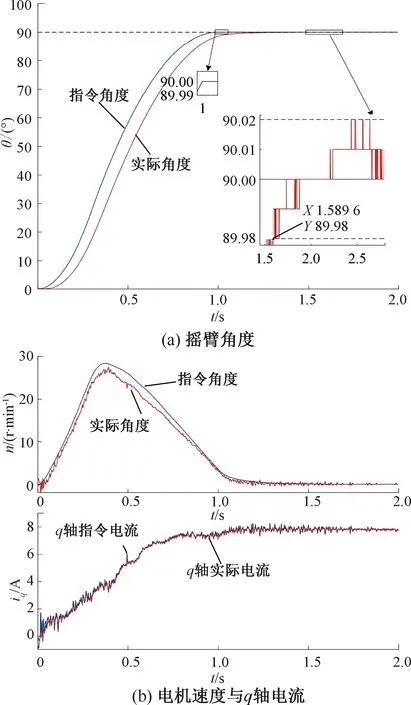
图8 双环PI算法实验结果图

如图8所示，达到所要求的位置精度所用时间为1.59 s，并且最终收敛于指令角度。

5.2 双环MPC实验分析

实验分别测量了MPCC与SS-MPCC运行一次所消耗的时间。采用MPCC算法，运行一次所需时间为4.65 μs。相同情况下，SS-MPCC运行一次耗时为2.37 μs，近乎是MPCC算法耗时的一半，较大程度减少了单次电流环计算时间。下述实验中，电流环控制算法为SS-MPCC。

在采用双环MPC算法的情况下，实验到位时间比仿真更短，仅有1.225 s，这同样比采用双环PI算法控制的实验到位时间少，缩短了0.365 s。但与仿真相同的是，MPC算法的电流振荡较PI算法更大，导致最终到位精度比PI算法略低，振荡略大。由此换来的是更小的逆变器损耗，以较小的代价换取较大的优点。

从图9(b)中可以看出，在采用双环MPC算法的情况下，速度误差更小，速度环的动态性能提高了。

图9 双环MPC算法实验结果图

5.3 温度实验分析

为检测逆变器的损耗，分别在双环PI算法和双环MPC算法下控制摇臂运动，两者角度指令和位置环参数完全一致。

控制摇臂在0°和90°来回摆动12次，分别测得相应控制算法下的逆变器温度变化情况。从图10和图11中可以看出，单次摆动摇臂的运动过程中，双环PI算法最高温升为13.12 ℃，而双环MPC算法最高温升为11.51 ℃；摇臂来回摆动12次过程中，双环PI算法最高温升为51.23 ℃，双环MPC算法最高温升为46.69 ℃。PI算法的温升更大，即该情况下逆变器开关切换频率更快，损耗更严重。

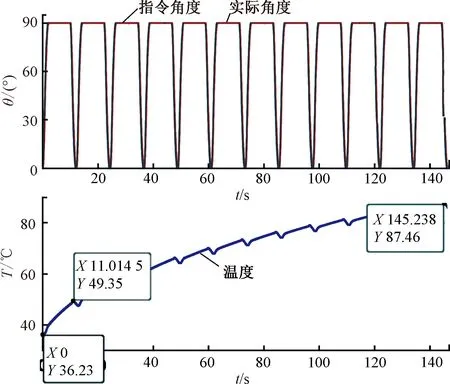
图10 双环PI算法摇臂角度与逆变器温度

图11 双环MPC算法摇臂角度与逆变器温度

6 结 语

本文提出了一种SS-MPCC算法，相比MPCC，缩小了候选矢量范围。该算法预先判断参考电压所在扇区，进而选出候选电压矢量，将所需计算的电压矢量数降至原有的一半以下，明显降低了计算时间，并通过实验进行证明。在此基础上，提出了一种带有ESO补偿的速度环模型预测控制算法，改善了速度控制的动态性能，使得电机的速度控制响应更快。本文采用双环MPC代替了传统的双环PI算法控制，并通过仿真和实验对比了两种算法的控制效果，双环MPC可以获得与双环PI相近甚至更好的动态响应性与稳定性。另外实验监测了逆变器的温度变化情况，在同样的控制条件下，双环MPC比双环PI的温升更低，逆变器的损耗更小。