在数学学习中促进学生深度思维

◎高春霞

(江苏省无锡市新吴区鸿山实验小学，江苏 无锡 214145)

深度学习是指在教师引领下，学生围绕着具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程数学是思维的科学，数学思维是学生数学活动的重要表现形式数学思维指的是学生在学习数学的过程中，产生的一种特定的思维方式，学生在学习和理解数学知识的时候，能够将理论知识形象化和具体化，最终完成学习任务教师应在活动中引发学生主动探究，在发现问题、解决问题的过程中发展学生的数学思维

一、在追问中打开学生思维

追问，就是追根究底地查问，是课堂教学中的一种策略，追问是一个相对完整的教学过程，它是有系列、有一定指向、最终能够使学生自主寻找正确答案的一种教学策略有效的追问可以拨动学生的思维琴弦，不仅能够引导学生对问题进行探索，而且能够引发学生思维的深化，提升学生的探究能力教师在小学数学教学中，抓好追问时机，准确把握住和学生交流的深度，才能提高课堂教学有效性在教学过程中，教师精心设计数学活动，让学生在活动中不断思考在动态的课堂中教师适时追问，不断促进学生思维的深入，从而达成有效学习

在教学“3的倍数特征”时，教师是这样设计的：

学生已经学习了2和5倍数的特征，出示计数器：

在计数器上有若干珠子，只调换一个珠子的位置，快速判断组成的数是否是2的倍数，学生调换珠子位置教师提问：“你发现什么？”学生会发现只要个位上珠子的个数是2、4、6、0时，组成的数都是2的倍数

大家猜测：3的倍数会有什么特征呢？

有的学生说个位上是3、6、9的数大家带着猜测进行验证：调换珠子的位置，发现无论怎样调换怎么也得不到3的倍数，进而引发学生思考，对刚才的猜测产生疑问，此时有的学生说3没有倍数、3的倍数没有特征等等

此时，教师去掉一颗珠子，让学生继续移动珠子，接下来，学生发现无论如何调换珠子的位置，组成的数都是3的倍数

所有学生都沉浸在兴奋中，教师追问：“这是怎么回事呢？”部分学生恍然大悟，脱口而出：“刚才是7颗珠子，现在是6颗珠子，6是3的倍数，所以怎样调换位置得到的数总是3的倍数”由此学生很容易想到：9个、12个、15个珠子组成的数也是3的倍数，珠子的个数也就是各个数位上的数的和进而教师借助百数表来探究3的倍数特征

本教学环节让学生经历体验的过程，经历由珠子个数的变化而组成的数直接决定其是否是3的倍数学生在解决问题时需要一个过程，其思维在不断地发展，思考在不断地深入，经历探究的过程后引发思维指向问题的本质，学生打开思维，在经历数学学习的过程中悟出知识的内在联系，从而将数学学习推向高阶思维

再如，在教学“圆的认识”时，教师这样设计：

出示情境：车轮一个是圆的，一个是方的

教师：为什么我们的车轮都做成圆形的呢？

学生：圆形的车轮光滑，圆在滚动时平稳

教师：说出了圆形车轮的好处，那为什么不做方形的车轮呢？

学生：方形在滚动的过程中一高一低，在滚动过程中颠簸不平稳

教师追问：方形的车轮在滚动的过程中一高一低是什么造成的呢？

学生：方形有四个角，方形的车轮在滚动过程中一会角着地，一会边着地，方形的车轮里面的拉条有的长，有的短……

在这样的对话中，教师自然地将学生的思维引向对问题本质的思考

好的课堂是师生互动、生生互动的课堂在数学课堂中，教师能否有效调动学生学习的积极性，很大程度上取决于教师设计的活动能否引发学生的思考，教师的追问是否促进了学生思维的深入因此，教师要善于创设学习情境，精心设计问题，有目的有层次的追问能够调动学生学习的兴趣，教师要通过巧妙的追问，引发学生深入思考与研究，促使学生不断地有新的发现与提升，培养学生良好的思维品质

二、在发现中发展学生思维

数学教学要发展学生的思维，在教学过程中教师应引导学生通过观察发现、总结规律并不断深化学习要达到良好的学习效果，教师就要精心设计问题，在教学“因数与倍数”时，教师这样设计：

6的因数有:( )

11的因数有：( )

20的因数有:( )

32的因数有：( )

在学生汇报环节，教师提问：“仔细观察，你发现了什么？”这样的问题设计遵循了学生的认知规律，也体现以学生为主体的教学理念，有利于学生主动思考学生回答：“这些因数里都有1，还都有这个数本身”有的学生认为数越大，它的因数越多，单数的因数比双数的因数少……教师紧紧抓住学生的发现追问：“对刚才这些发现你有想说的吗？”这时学生都处于积极的思考状态有的学生回答：“6的因数有1、2、3、6四个，11的因数有1和11两个，并不是数越大因数越多”这时教室里响起了掌声接着又有同学说数越大因数不一定越多大家产生了疑问，教师不急于对学生的回答进行评价，而是请大家在练习本上自己举例，验证一下自己的想法

我们在留给学生发现的时间和空间后，要及时对学生产生的问题进行处理，在日常的教学中，教师容易急于求成，问题一旦抛出，就希望学生能够回答出正确的答案在教学中，我们要把学生放在学习的主体位置上，不能教师牵着学生的鼻子走，我们的课堂是知识生成的课堂，生生互动的课堂，让学生思维发散的课堂本教学环节设计中，教师给学生提供了学习的空间，抓住了生成的问题正是这些生成的问题，才给学生创造了探究的空间，将学习层层推进我们教师所起的作用就是适时点拨引领，让学生的思维得到充分发展

三、在探究中深化学生思维

著名数学家波利亚说：“学习任何知识的最佳途径是自己去发现”因此有效的课堂教学，应给学生足够的思维空间小学生由于年龄特点和能力水平的限制，探索与实践意识和能力比较弱，在数学课堂教学中，教师应根据学生的实际情况适当地引导学生去探索、发现、解决问题，让学生体验数学学习的过程

在教学“认识线段”一课时，学生在认识线段后，教师是这样设计教学环节的：

出示一张圆形纸片，让学生自己尝试在圆形纸片上找寻线段

有的学生用直尺在圆形纸片上画出一条线段，有的学生用折一折的方法，有的学生用剪刀把圆形纸片剪成两份找到了线段

通过找一找的活动，学生创造出了不同的线段，每个学生的思维都很活跃，学习热情高涨学生在学习过程中感受到了成功的喜悦，思维被打开，将学习推向高阶思维

再如，在教学“分数的初步认识”时，在学生认识二分之一的基础上，教师设计了这样的教学环节：

利用在长方形纸条找到的三分之一，并说一说你是怎样找到的

学生经过自主探究后进行汇报，有的学生用尺子量一量再平均分，然后找到了纸条的三分之一；有的学生仿照寻找二分之一的方法通过折一折寻找三分之一

正当教师进行总结时有一名学生把手举起，他在纸条上画出了一条线，再寻找这条线的三分之一，这一种方法是教师没有预设到的，进而问：你是怎样想的呢？

学生回答：二分之一可以通过对折平均分，可是我尝试将这张纸条平均分成三份没法对折，要求是只要在这张纸上面找到三分之一就可以，于是我就画了一条线，用直尺量一量，再将其平均分成三份，每一份就是这条线的三分之一

一个不经意间的设计，让教师发现学生的想象能力及解决问题的能力超乎了教师的想象在经历寻找分数的过程中，学生逐渐明确了“平均分”是分数产生最本质的意义，学生已经将分数的意义内化于心，抓住分数含义的本质，简短的教学设计呈现了学生由具体的形象去理解分数的含义，再到抽象的理解过程

小学生思维的特点是以具体形象思维为主要形式，逐步转变为抽象逻辑思维形式，但抽象思维仍然需要借助直观形象来实现，这个过程不是能立刻完成的，而是一个较为复杂而循序渐进的过程在教学过程教师要培养学生创造性思维、发散性思维，

在教学分数比较大小后，教师设计了这样的拓展练习：

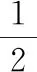
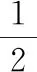
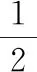
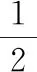
此时教师将学生微微推向学习的高潮，全班同学陷入深深的思考之中，教师让学生带着好奇心下课，在课后继续研究这些位置上到底会是哪些数

在我们的教学中要充分体现学生的主体地位，激发学生的能动性和创造性，教师要给学生提供开放的具有探究空间的活动，让学生参与经历思考的全过程，为学生创造表达自己想法的机会和空间开放的活动能够激励学生深入地思考，能够促进学生多元思考，我们要听到来自学生的不同声音，看到学生不一样的呈现方式要想激活学生思维，教师就需要创设学习的活动空间在教学中，我们要善于激发学生学习的兴趣，尊重学生独立思考的成果，保护学生的独特想法，挖掘学生的潜能，鼓励学生大胆地尝试在课堂上，教师要把学习的主动权交给学生，多给学生一些思考的时间和动手操作的空间，让学生多一份创造的信心和成功的体验，培养学生的创造能力

四、在活动中拓展学生思维

教学过程本身是一个动态的过程，学生的原有经验、知识结构、个性等多方面的差异性决定了学生学习过程是复杂的因此，教师在教学设计的过程中，应充分考虑学生的认知规律，以及学生课堂上可能出现的情况，从而使整个教学设计留有更大的空间教师的教学设计要符合学生的认知规律和实际情况，使课堂教学沿着预设的轨道前进但教学过程是随时变化的，学生的学习情况经常与教师的预案有所差距此时，教师应运用教学策略机智改变原来的教学方案以适应学生，充分挖掘学生潜能，让师生在互动的教学过程中得到共同发展，给学生张扬个性的机会，让学生的思维得到拓展，创新潜能得以挖掘

例如，在教学“观察物体”一课时，有一个教学环节是这样设计的：

每个小组四个同学，分别坐在小熊玩具的前后左右的位置，教师给每个同学准备了一个信封，信封里有从前后左右观察到小熊的图片，然后让坐在小熊左面的同学从信封中找到观察到小熊对应的图片，其他三名同学猜一猜刚刚那名同学看到小熊的样子，从信封中找到相应的图片

教师提问坐在小熊前面的同学：你选的是哪一张图片，为什么？

学生回答选择本张图片的理由：坐在小熊左面看到小熊的左手，脸是朝向左面的，尾巴是朝向右面的……

学生说出自己判断的根据，抓住观察物体本身的特征，通过自己的想象来做出最终的判断

本教学环节教师让一名学生观察，其他学生通过想象推理做出判断

再如，教师出示一个茶壶，让学生先想一想站在茶壶的前后左右分别看到的茶壶的样子，然后在练习本上画一画，最后让学生说一说自己是怎么想的在这个过程中，学生不仅学会观察物体，还能够借助自己原有的经验和自己的想象分析，培养空间想象能力和推理判断能力

又如，在教学“解决问题的策略”时，教师是这样设计的：

一根长22米的绳子围一个长方形的花园，面积最大是多少？

学生自己尝试探究学生用列表的方法展示：

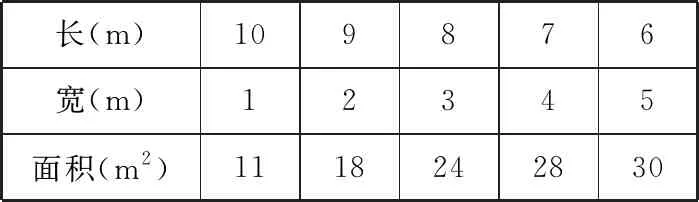
长(m)109876宽(m)12345面积(m2)1118242830

教师：你们发现了什么？

学生1：一组一组列举就会发现长是6米，宽是5米时，长方形面积最大

学生2：我发现长与宽的差越小，面积就越大

学生3：当长与宽的差是0时，面积最大

学生:4：当长与宽的差是0，那么就变成正方形了，这时面积应该最大

这时教师没有阻止学生的思维，进而问：大家觉得呢？

生1：那边长就变成小数了，可是我们没有学习小数乘法

这时教师拿出计算器投屏展示计算过程：55×55=3025，学生发现当围成正方形时面积最大然而到这里教师的教学并没有停止，而是教师顺着学生的思维继续问：“大家想一想，我们继续围下去，难道只有正方形的面积最大吗？闭上眼睛想一想围成正五边形、六边形……最后形成圆形，你们推理一下，什么时候面积最大？”这时学生陷入深深的思考之中，部分学生认为是围成圆形时面积最大，然后教师出示圆的面积大约是38平方米整个教学过程的设计将学生的学习推向更深入的思考之中

思维能力的培养和提高离不开学生的实践，在教学中，教师应当合理引导学生大胆思考，鼓励他们敢想、敢问、敢说，充分发挥学生学习主体的作用同时，教师要转换方法，鼓励矛盾的产生，而不是一味追求和谐、统一的标准答案，要给每个同学公平的机会阐述自己的想法，鼓励他们大胆陈述，引导学生自主学习，使学生理解和掌握数学知识和思想，形成自己的思维习惯，同时帮助学生掌握高效的学习方法，养成良好的思维能力和思维品质在课堂教学中，教师要充分给予学生思考的空间和时间，以思维训练作为教学的核心