超临界二氧化碳向心透平研究进展

李 红，廖鹏飞，何 青

（华北电力大学能源动力与机械工程学院，北京 102206）

超临界二氧化碳（supercritical carbon dioxide，S-CO2）指压力和温度均在临界点（7.38 MPa，31 ℃）之上的二氧化碳[1]，具有良好的物性特征。从循环工质选择的角度看，S-CO2具备二氧化碳储量丰富、环境友好、化学性质稳定、廉价易得等优点；对于以S-CO2作为工质的动力循环来说，S-CO2具有功率密度大和传热能力高等优点。同时，二氧化碳临界温度与环境温度接近，因此S-CO2动力循环发电系统的低温端放热和工质的超临界状态更容易实现。随着S-CO2布雷顿循环的兴起，S-CO2在太阳能、核能和燃煤等发电领域得到了蓬勃发展[2]。

向心透平是指工质沿着转动轴半径方向朝轴心方向流动的动力式机械，是可以将工质能量转化为轴功输出的设备，一般包括蜗壳、喷嘴、叶轮3个部分，是动力循环的核心部件[3]。图1为某MW级S-CO2向心透平结构[4]。由于向心透平造价低廉，结构紧凑，焓降大，在流量较小的设计条件下也可以达到较高效率[5-6]。因此，向心透平常被用作各种动力循环发电系统的热功转换设备，是发电系统工程应用的基础。Uusitalo等人[7]认为轴流式透平适合用于10 MW以上规模的S-CO2动力系统，而向心透平被认为是功率水平低于10 MW的小型S-CO2动力系统更可行的选择。因此，研究S-CO2向心透平意义重大。

图1 某MW级S-CO2向心透平结构[4]Fig.1 Structure of a MW-class S-CO2 radial-inflow turbine[4]

在S-CO2向心透平的设计过程中，S-CO2向心涡轮的损失模型和设计方法多借鉴空气等其他工质向心透平的损失模型和设计方法，但这样做是否可靠有待验证。为了考虑黏性对S-CO2向心透平出口气流角的影响，通常在通流计算中使用落后角模型。准确计算落后角是预测向心透平性能的重要前提。在实际运行过程中，为保证S-CO2向心透平运行的稳定性，还要考虑S-CO2向心透平的密封方式、轴承的选择以及轴向力的控制等问题。基于此，本文从理论和实验2个角度总结S-CO2向心透平的研究进展，并分析现存理论的难点和技术瓶颈，为SCO2向心透平的发展提供指导。

1 理论研究

S-CO2向心透平的理论研究通常包括透平的设计和气动性能研究。透平的设计主要包括一维热力设计、造型设计、气动分析等部分。S-CO2向心透平的一维热力设计基于一元流动理论，配合连续性方程、能量方程、动量方程等确定各个特征点上的热力参数，最终得到通流部分主要几何参数。热力设计是透平总体设计中极其重要的一环，但一维热力设计的结果并不一定是最优结果，所以将一维热力设计与优化算法相结合来寻找最佳参数的一维优化设计方法具有良好的前景。S-CO2向心透平的损失模型和落后角模型是一维优化设计方法中确定损失和计算气流出气角的依据，对设计结果具有重大影响。透平性能研究主要是依据透平内部的流场、速度场、压力场和温度场来分析透平内部整体流动状况。本章分别从S-CO2向心透平的损失模型、落后角模型、一维优化设计方法和气动性能角度总结相关研究进展。

1.1 损失模型

在S-CO2向心透平的一维热力计算中，损失模型是准确计算流动损失的关键，对设计结果精度影响重大，一般包括静子损失、攻角损失、通道损失、叶尖间隙损失、风阻损失、余速损失和尾迹损失。

Uusitalo等人[8]研究发现，S-CO2向心透平的主要损失是通道、叶尖间隙、出口动能和定子损失，占总涡轮损失95%以上，其他损失对总涡轮损失的贡献很小。Qi等人[9]研究发现，通道损失和叶尖间隙损失是主要的损失来源。Lv等人[10]评估了6组损失模型（主要区别在于通道损失和叶尖间隙损失）的精确性，对Wasserbauer[11]、Moustapha[12]、Rahbar[13]的通道损失模型和Moustapha[12]、Saravanamuttoo[14]的叶尖间隙损失模型进行排列组合，并分为6组验证，对比了使用不同损失模型的性能预测结果，发现使用通道损失模型和叶尖间隙损失模型分别为Wasserbauer与Moustapha组合和Wasserbauer与Saravanamuttoo组合的计算流体力学（computational fluid dynamics，CFD）数据与实验数据比较吻合；在考虑总膨胀率的情况下，Lv等人选择的通道损失模型和叶尖损失模型为Wasserbauer与Moustapha组合。

Balje[15]、Wasserbauer[11]、Moustapha[12]等人提出了3种通道损失模型，其中Balje的通道损失模型考虑了速度对损失的影响，后2种模型同时考虑了速度和通道曲率对损失的影响。此外，只有Wasserbauer的通道损失模型考虑了转子的实际尺寸对损失的影响。Balje的通道损失模型被Lee[16]和Uusitalo[17]在研究中使用，Wasserbauer的通道损失模型被Lv[10]应用于设计S-CO2向心透平，Moustapha的通道损失模型被Uusitalo等人[8]用于分析S-CO2向心透平的性能。Uusitalo等人[7]对比分析了上述3种损失关系式在S-CO2向心透平设计中的准确性，发现Wasserbauer通道损失模型与CFD结果吻合更好。Wasserbauer通道损失模型为：

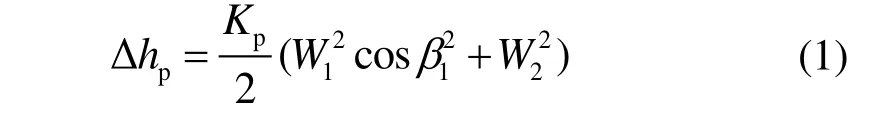
式中：Δhp为通道损失焓，J/kg；Kp为通道损失系数；W1为叶轮入口相对流速，m/s；W2为叶轮出口相对流速，m/s；β1为叶轮入口相对气流角。

Moustapha的叶尖间隙损失模型为：

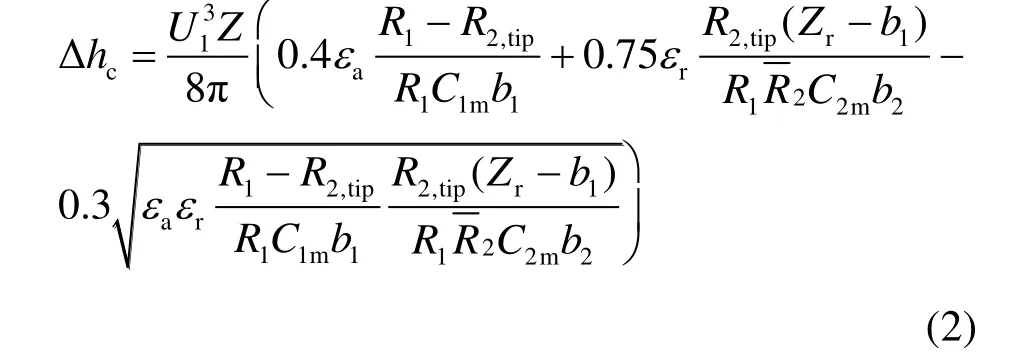
式中：Δhc为叶尖间隙损失焓，J/kg；U1为叶轮周速，m/s；Z为叶轮叶片数；εa为轴向叶尖间隙，m；εr为径向叶尖间隙，m；R1为叶轮入口半径，m；R2,tip为叶轮出口叶顶半径，m；为叶轮出口平均半径，m；C1m为叶轮入口绝对流速的子午分速，m/s；C2m为叶轮出口绝对流速的子午分速，m/s；Zr为叶轮轴向长度，m；b1为叶轮入口叶高，m；b2为叶轮出口叶高，m。

Qi[9]和Moustapha[12]等人提出的叶尖间隙损失模型考虑了轴向间隙和径向间隙以及两者耦合项的影响。Qi的叶尖间隙损失模型（式(3)）适用于高叶尖间隙比的小型透平。

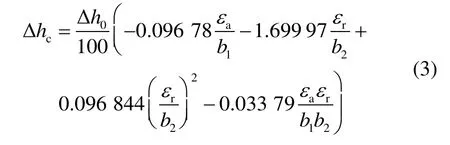
式中：Δh0为透平等熵焓降，J/kg。

Jansen[18]的叶尖间隙损失模型（见式(4)）默认轴向间隙和径向间隙相等，此模型被Lee等人[19]应用于一种S-CO2向心透平的设计中。

式中：tc为叶尖间隙，m；b1为叶轮入口叶高，m；R2,hub为叶轮出口叶根半径，m；C1θ为叶轮入口绝对流速的圆周分速，m/s；ρ1为叶轮入口密度，kg/m3；ρ2为叶轮出口密度，kg/m3。

表1总结了Uusitalo[8]、Lv[10]、Qi[9]3种损失模型的配置，其中出口动能损失Δhe由式(5)确定，在表1中未体现。

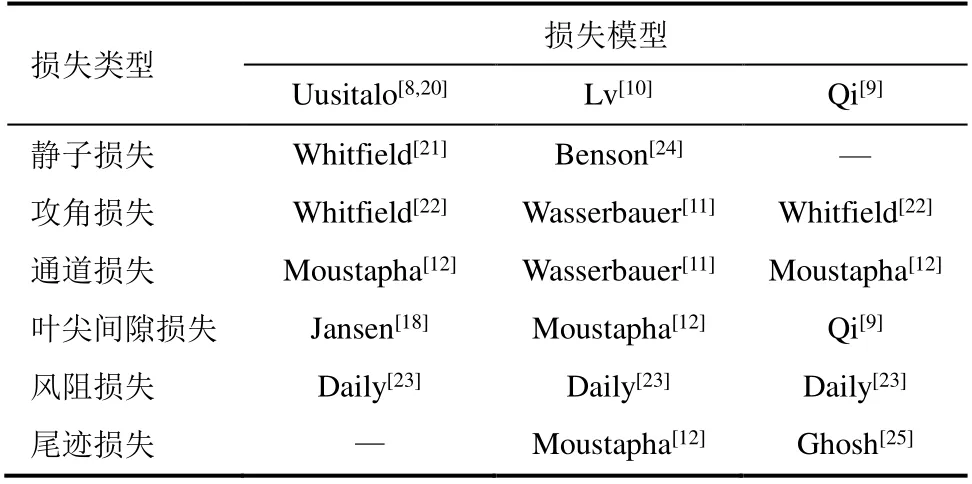
表1 3种损失模型的配置Tab.1 Configuration of the above three loss models

式中：C2为叶轮出口绝对流速，m/s。

1.2 落后角模型

与损失模型相同，落后角模型也是一维热力计算的关键，对设计结果的精度影响重大。气流的落后角通常指气流离开叶栅时的出气角与叶栅几何构造角之差。叶栅出口马赫数和尾缘厚度都是影响落后角的重要参数。S-CO2向心透平落后角模型的研究可以借鉴其他工质透平落后角模型。目前，对于S-CO2向心透平落后角模型的研究还未引起广泛的重视。

文献[26]给出了航空发动机中轴流式透平落后角的计算公式（式(6)）。首先，确定马赫数为0.5和1.0时的落后角，然后对两者进行插值求得马赫数在0.5～1.0的落后角。马赫数大于1.0时的落后角取马赫数为1.0时的落后角的值。

当Ma≤0.5时：

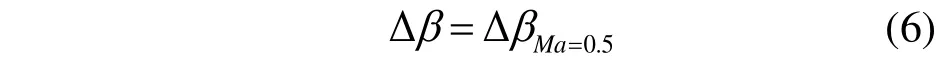
当0.5＜Ma＜1.0时：

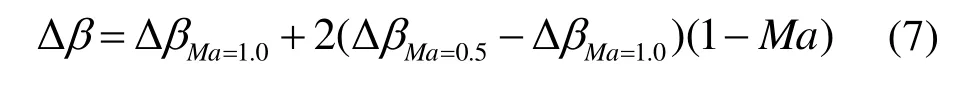
当Ma≥1.0时：

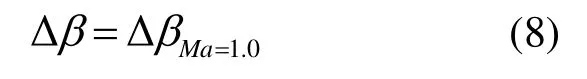
式中：Δβ为落后角；Ma为出口马赫数。其中，ΔβMa=0.5和ΔβMa=1.0可通过查阅文献[26]中马赫数与落后角的曲线关系图求得。姜晓武[27]使用的落后角模型和文献[26]类似，也使用插值法并主要针对亚声速气流角，对于超声速气流角则用堵塞流量确定。

西安交通大学邓清华等[28]针对100 kW微型燃气轮机向心透平静叶落后角进行了深入的研究，分析了马赫数和叶片尾缘厚度对气流落后角的影响。通过实验和数值分析发现，落后角在马赫数为0.5～1.2范围内变化相当大，并且在马赫数为0.9之前变化较为平缓，在马赫数为0.9之后变化较为剧烈。马赫数和叶片尾缘厚度的变化引起落后角的变化关系为：

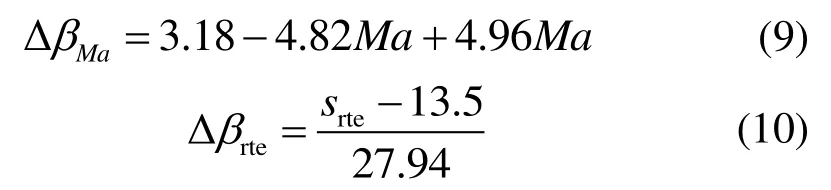
式中：srte为尾缘厚度与喉部宽度的比值，%。

1.3 一维优化设计方法

一维热力设计是多参数相互制约、相互影响的过程。目前，热力设计已有成熟方法[6]。相对于气动分析，热力设计的计算速度更快捷，但给出的结果并不一定是最优的。优化算法可以在一定的约束条件下，在众多参数或方案中挑选出最优参数或最优方案，常见的有遗传算法和模拟退火算法等。将一维热力设计与优化算法程序相结合既能节省大量时间又能保证设计较好地符合要求。在S-CO2向心透平的一维热力设计过程中引入优化算法是目前S-CO2向心透平设计领域研究的热点。

李翔宇等[29]基于谢菲尔德遗传算法理念开发了一套多约束条件下向心透平热力优化设计程序和变工况性能预测程序，优化设计程序选取速比、反动度等8个参数为约束参数，并以轴效率为目标函数，该方案总体性能参数与数值模拟计算结果的偏差均小于3%。Wang等人[30]将优化算法程序与传统设计过程相结合，改进了模拟退火算法，建立了包含转子子午面和喷嘴轮廓优化的优化过程，通过建立粗网格仿真代理模型，实现了快速设计和性能优化。施东波等[31]结合模拟退火算法和机器学习中Gauss过程回归方法开发了一套S-CO2向心透平的优化设计方法，通过预估热力设计结果，筛除较差的工况，保证较优的工况点被用于气动分析来提高透平设计的效率，同时每个被气动分析的工况点都会被作为新的数据，使得该方法不断更新，结合模拟退火算法，该优化设计方法具备全局优化的特点。Lv等人[10]提出了一种使用逐步二次规划的S-CO2向心透平的优化设计方法，可以快速收敛到最优解，并通过将原始问题转化为一系列近似二次规划子问题来求解约束非线性优化问题；以总静效率为优化目标，对比了逐步二次规划算法和遗传算法的收敛速度，发现前者只用6步就能得到最优解，而后者需500步以上才能得到相同的最优解。

表2总结了使用基于遗传算法、Gauss过程回归和逐步二次规划的优化设计方法的效率。由表2可见：基于遗传算法的优化设计方法效率误差最小，但小于设计效率；基于Gauss过程回归的优化设计方法的效率误差最大，但高于设计效率。

表2 3种设计方法效率比较 单位：%Tab.2 The efficiencies of three design methods

1.4 气动性能研究

三维数值模拟借助ANSYS-CFX和NUMECA等软件，基于控制方程和湍流方程给出透平的动静叶通道的压力场、速度场、温度场和熵分布云图等，借此分析向心透平的气动性能。

昆士兰大学的Odabaee等人[32]使用ANSYSCFX软件对透平进行气动性能分析，发现使用真实气体方程模拟真实气体性质时存在较大误差，而使用来自NIST REFPROP的真实气体性质（real gas property, RGP）表的方法来计算物性比较准确。Ameli等人[33]分析了不同分辨率的RGP表对透平性能的影响。

吕国川[34]分析了轮背空腔泄漏流体的流动情况，发现轮背空腔泄漏流造成的各种损失会对S-CO2向心透平的效率产生显著影响，如泄漏损失、回流损失等。图2为作者设计的喷嘴、叶轮以及轮背空腔在子午面的速度场分布[34]。从图2可以发现，轮背空腔在2个转角处均出现阶梯涡。

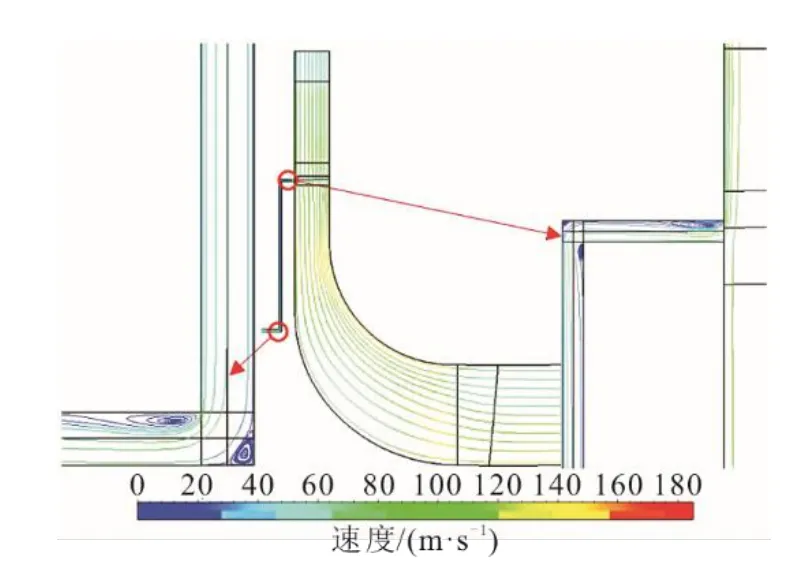
图2 喷嘴、叶轮以及轮背空腔在子午面速度场分布[34]Fig.2 Flow field distribution on meridional plane of nozzle,impleller and wheel back cavity[34]

图3为轮背空腔子午面示意[34]。由图3可以发现，轮背空腔径向间隙进口处泄漏流在压力面附近的轴向速度（流入空腔方向）最大。Yang等人[35]探究了向心透平叶轮轮背空腔内工质的流动对叶轮轴向力和透平性能的影响，并分析了不同类型迷宫密封的密封性能。Zhou等人[36]探究了S-CO2向心透平的叶尖泄漏特性，分析了叶尖间隙与透平效率的关系。

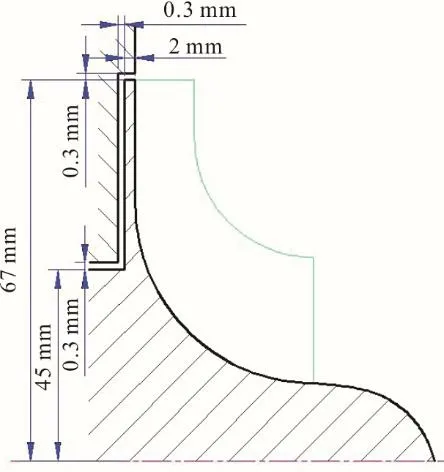
图3 轮背空腔子午面示意及基本尺寸[34]Fig.3 Schematic diagram and basic dimensions of wheel back cavity[34]

Lee等人[37]发现：在进出口压比较高（2.00）时，S-CO2向心透平转子通道内工质流动较均匀，而在进出口压比较低（1.33）时，转子通道内工质流动出现较大二次流；质量流量低于设计点过大时会产生过多的二次流损失。西安交通大学王雨琦等[38]对部分进气度为0.3的S-CO2向心透平展开气动性能分析，图4[38]是其研究的S-CO2向心透平50%叶高截面熵分布。从图4可以发现，靠近喷嘴及动叶壁面边界层的流体由于摩擦损失产生了较小的熵增，在非进气弧段内，工质在动叶流道内产生较大的旋涡，出现明显的熵增。

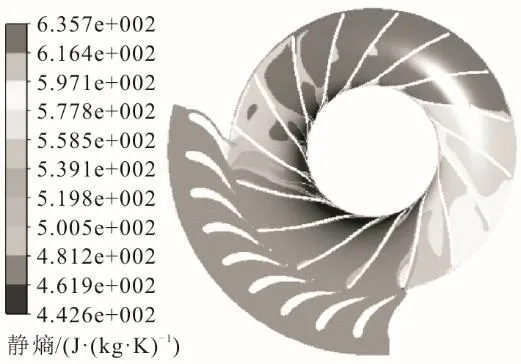
图4 50%叶高截面熵分布[38]Fig.4 Entropy distribution in 50% leaf height section[38]

S-CO2的跨临界现象指二氧化碳从超临界状态转换为亚临界状态的现象，会导致气动性能不稳定。Wang等人[39]在研究中发现转子叶片的尾缘尖端出现跨临界现象，且随着尾缘节距减小，跨临界区域面积增大。周奥铮等[40]对S-CO2向心透平展开气动性能研究，通过分析透平内部流场，发现S-CO2工质经过喷嘴通道时膨胀加速，压力降低，此后进入动叶流道继续膨胀；而分析透平内部马赫数云发现，在导向叶栅喉部工质流速相对较高，在动叶压力面附近出现速度较低区域，整个过程中流动处于亚音速状态。

2 实验研究

美国、韩国、日本、中国等国家已经在实验系统中投入使用了S-CO2向心透平设备。

美国桑迪亚国家实验室（Sandia National Lab，SNL）建造的S-CO2布雷顿循环实验回路使用的涡轮机械是由向心透平、交流发电机和离心压缩机组成的透平-交流发电机-压缩机（turbo-alternatorcompressor，TAC）设备。该设备可以有效地平衡向心透平和压缩机产生的轴向力。SNL还在系统中加装了扫气增压泵以排出向心透平的多余泄漏流并减少风阻损失。向心透平采用定制的迷宫密封[41]。2018年，SNL购买了一款向心透平设备，该设备的叶轮和轮毂使用直接金属激光烧结而成[42]。美国一家公司（Bechtel Marine Propulsion Corporation，BMPC）在其设计的S-CO2布雷顿循环系统中使用了向心透平[43-44]，测试人员在实验结束后发现喷嘴叶片尖端处已经磨损并弯曲到流道中，通过分析系统是否加装过滤器，发现该现象是由回路中存在的微小颗粒导致的[44]。

韩国能源研究院（Korea Institute of Energy Research，KIER）的Cho等人[45]开发了一个简单的S-CO2布雷顿循环实验回路，与SNL和BMPC相同，为控制泄漏流，使用了迷宫密封[44]。韩国Ahn等人[46]以及韩国原子能研究所（Korea Atomic Energy Research Institute，KAERI）的Cha等人[47]设计了S-CO2实验回路，与SNL使用的TAC涡轮机械不同，该团队使用的透平和压缩机是分开工作的。这种结构设计是为了测试S-CO2朗肯循环特性，可使向心透平的设计和运行具有更大的灵活性。该团队设计的透平是带冠式的，主要目的是消除透平前后的压差，进而控制轴向力。

日本东京工业大学（Tokyo Institute of Technology，TIT）的Utamura等人[48-49]在S-CO2闭式布雷顿循环实验装置中向心透平的入口处安装了高效微粒空气过滤器，以防止异物进入。

英国Bianchi等人[50]也研究了S-CO2向心透平，与SNL相同，以商业化为目的[41,50]。

我国西安热工研究院（Xi’an Thermal Power Research Institute，TPRI）李红智等[51]搭建了S-CO2动力循环实验台，其向心透平转速为30 000 r/min，位于轴的一阶和二阶临界转速之间。透平叶轮材料使用耐高温高压和具有高强度特性的Inconel 718合金。在对高压向心透平的受力性能进行模拟分析时，考虑了离心力和压力载荷。图5[51]为TPRI高压向心透平叶轮的von Mises应力。向心透平叶轮最大等效应力远小于许用应力，叶片根部靠前缘附近的位置出现峰值应力。

图5 TPRI高压向心透平的von Mises应力[51]Fig.5 Von Mises stress of high pressure radial turbine used in TPRI[51]

上海汽轮机厂有限公司设计装配了一台透平压缩机同轴一体机，主要包括向心透平叶轮、压缩机叶轮、轴承、齿轮等，向心透平采用干气密封[52]。

中国科学院大学陈俊斌[53]为了解决S-CO2向心透平干气密封工作环境温度过高的问题，设计了S-CO2向心透平旋转冷却实验系统，分别从理论和试验角度分析了工质流动过程中的换热规律。

表3为SNL、TIT、KIER、TPRI实验中使用的向心透平的设计参数[45,51,54]。

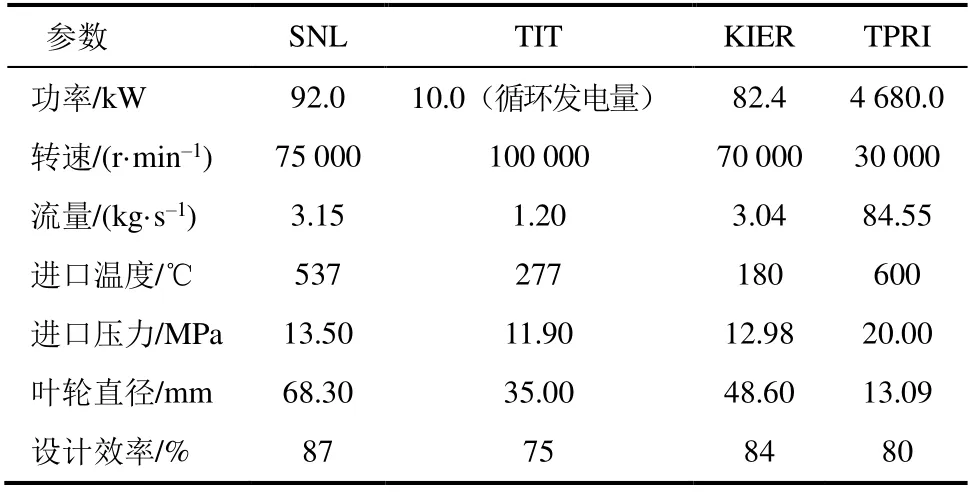
表3 实验用超临界二氧化碳向心透平设计参数Tab.3 Design parameters of S-CO2 radial turbine for experiments

由表3可以看出，S-CO2向心透平的尺寸较小，转速较高。SNL、BMPC、KIER的向心透平均使用了迷宫密封。SNL考虑过气体浮环密封，尽管其密封效果优于迷宫密封，但因其系统和结构比较复杂，且在小型向心透平上未有商业应用，所以未被选择。BMPC在考虑转速的情况下，也并未选择密封效果更好的干气密封等方式。中国科学院大学陈俊斌[53]针对S-CO2向心透平干气密封的热安全问题展开了技术研究。上海汽轮机厂有限公司最近的研究表明，其透平压缩机同轴一体机中的向心透平已使用了干气密封，并已完成加工装配。迷宫密封是S-CO2向心透平常用的密封方式，但是泄漏量较大。干气密封的密封效果较好但受小尺寸和高转速以及高温工质的限制，市场上很难有能满足其条件的干气密封产品。S-CO2向心透平的密封技术仍然需要研究和发展。

3 结论与展望

1）目前对于S-CO2向心透平损失模型的研究尚处于起步阶段，本文仅对比了通道损失模型和叶尖损失模型。未来可对现有各损失模型进行对比筛选，同时开发专门针对S-CO2向心透平的损失模型。此外，还可以进一步探究向心透平优化设计方法，以完善S-CO2向心透平设计过程。

2）目前对于轴流透平和压气机叶栅落后角的评估已有大量的理论和试验数据来指导，而对于SCO2向心透平落后角模型的研究还鲜有文献报道。未来可加大对向心透平和S-CO2向心透平落后角的分析和研究，借鉴轴流透平和压气机关于叶栅落后角的研究方法来计算落后角，如利用神经网络建立代理模型。

3）目前关于S-CO2向心透平的气动性能分析的研究较少，未来可以进一步探究透平内部的气动性能以及各种设计参数对向心透平性能的影响。二氧化碳近临界区域的物性波动剧烈，相关膨胀相变过程较为复杂，对数值计算结果和气动性能具有较大影响。未来，提高近临界区域热物性计算精度以及研究和控制透平中跨临界现象是重点。

4）目前针对S-CO2向心透平的密封研究比较少。未来可加大该方面的研究，包括密封方式、密封的泄漏特性、传热特性、气体激振动力特性的研究等。此外，S-CO2向心透平的轴承的选择以及轴向力的控制等问题需要专门的研究与设计。