Deep learning-based time-varying channel estimation with basis expansion model for MIMO-OFDM system①

HU Bo (呼 博), YANG Lihua, REN Lulu, NIE Qian

(College of Communication and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,P.R.China)

Abstract For high-speed mobile MIMO-OFDM system,a low-complexity deep learning (DL) based timevarying channel estimation scheme is proposed. To reduce the number of estimated parameters, the basis expansion model (BEM) is employed to model the time-varying channel, which converts the channel estimation into the estimation of the basis coefficient. Specifically, the initial basis coefficients are firstly used to train the neural network in an offline manner, and then the high-precision channel estimation can be obtained by small number of inputs. Moreover, the linear minimum mean square error (LMMSE) estimated channel is considered for the loss function in training phase,which makes the proposed method more practical. Simulation results show that the proposed method has a better performance and lower computational complexity compared with the available schemes,and it is robust to the fast time-varying channel in the high-speed mobile scenarios.

Key words: MIMO-OFDM, high-speed mobile, time-varying channel, deep learning (DL),basis expansion model (BEM)

0 Introduction

In the high-speed mobile scenarios supported by 5G or beyond 5G communication systems, such as high-speed railway, ultra-high-speed rail railway, and low orbit satellite, the higher mobile speed and larger carrier frequency make the design of high-speed mobile wireless communication systems more challenging. In the high-speed mobile scenarios, the high-precision channel estimation is important, which seriously affects the performance of the systems[1-3].

In recent years, the deep learning (DL) based time-varying channel estimation has widely attracted interest of many researchers. It mainly uses the neural networks to learn the channel characteristics[4-8]. In Ref.[4], a deep neural network (DNN) based channel estimation was given, where the historical channel estimation and the whole received signal were collected to train DNN. Although it has good performance,it has too many input samples, which causes large computational complexity. Ref.[5] presented a channel estimation scheme of jointing DL and decision-directed(DD), where the channel estimation of pilot was used as the input of the network to obtain the channel of data symbol, and then the high-precision channel estimation can be obtained by the DD processing on the data symbol. However, the combination of DL and DD will bring high computational complexity. In Ref.[6], the convolutional neural network (CNN) and recurrent neural network (RNN) were jointly used to estimate the channel, while it has a complex network structure.To avoid the performance loss caused by the random initialization of network, a DL-based channel estimation method with pre-training was given in Ref.[7],which requires the pre-training and training in an offline manner to obtain the network model with optimal parameters, but it also has high complexity. A RNNbased scheme was discussed in Ref.[8],where a sliding bidirectional gated recurrent unit is adopted to extract the features of input data, but the increase of the length of sliding window leads to a sharp rise in complexity, which makes the network difficult to converge.

Due to the complex network structure or excessive input sample parameters, these existing algorithms in Refs[4-8] had high computational complexity, which limited their practical application. In addition, most of previous DL-based techniques in Refs[4-8] adopted the perfect and noiseless channel information during the training phase for the loss function, which will make the existing DL-based algorithms impractical.

To solve the above problems, a low-complexity channel estimation method is proposed for the MIMOOFDM system based on DL and basis expansion model(BEM), which only uses the base coefficients and receives pilots to train the network. Moreover, the linear minimum mean square error (LMMSE) based pre-processed channel estimation (not the true channel) is considered in the training phase for the loss function.

The rest of this paper is organized as follows. Section 1 introduces the signal model. Section 2 presents the proposed method in detail. The simulation results and conclusions are given in Section 3 and Section 4 respectively.

1 Signal model

1.1 System model

1.2 BEM channel model

2 Proposed channel estimation method

In the field of DL, back propagation (BP) neural network is a multi-layer feed forward neural network,which is trained by the error back propagation algorithm. BP neural network has a strong nonlinear mapping ability and a wide range of applications[13-15].Considering the complex correlation of data in highspeed mobile scenario, BP neural network is employed to estimate time-varying channel in the proposed method. In the section,the framework of BP neural network is briefly introduced at first, and then the proposed method is given in detail.

2.1 BP neural network

In the proposed method, a single hidden layer BP neural network is adopted, which is shown in Fig.1. It is assumed that BP neural network includesDneurons in input layer,Eneurons in hidden layer andRneurons in output layer. The nonlinear mapping between input and output of the neural network can be expressed as(2)(1)

Fig.1 The structure of BP neural network

2.2 BP-based channel estimation with BEM

The proposed method is mainly divided into two phases: training phase and estimating phase. Based on the received pilot signal,the base coefficient estimation is firstly obtained. Then, the basis coefficient estimation and the received pilot are employed to construct samples to train BP neural network in an offline manner. Finally, an accurate estimation of the current channel can be directly obtained by the trained network.

Since the process of channel estimation between each transmitting and receiving antenna is the same and the pilots at different antennas are orthogonal, the index of the antenna (nt,nr) will be omitted in the following.

(1) Basis coefficient estimation

As the polynomial BEM (P-BEM) can effectively overcome the Doppler leakage and the channel edge model error caused by CE-BEM[12], the time-varying channel will be modeled by P-BEM in the proposed method, whoseqthbasis function can be written as

(2) Training phase

Construct training sample sets by the basis coefficient estimation in Eq.(16) and the received pilots,i.e.,

Judge of her astonishment35 when she saw that he was holding in his hand a portrait of herself! In vain did she puzzle over the apparent contradictoriness36 of his behaviour

Since the real-valued neural network is relatively simple and easy to implement, the real neural network is used to estimate the channel. Therefore, the training sample in Eq.(18) can be rewritten as

where Ξ(·) represents operation of converting data in complex domain into real domain, and Ξ(x) =[Re(x), Im(x)].

Based on the training sample sets given in Eq.(20), one can initialize the parameters of the network randomly and update the network parameters with the quantized conjugate gradient descent scheme, and then the potential relationship between the input and output can be learned by adjusting the network parameters.

(3) Estimating phase

In the estimating phase, based on the received pilots and the basis coefficient estimation, the trained BP neural network is used for real-time channel estimation. Assume that the input of the network is

whereΨ(·) represents reverse operation of converting data in real domain into complex domain.

2.3 Complexity analysis

Table 1 gives the comparison of computational complexity of different channel estimation methods. In Table 1, results for the LS estimator with linear interpolation, the DNN-based scheme with two hidden layers in Ref.[4],and the DL-based channel estimation with pre-training in Ref.[7] are also given. The number of floating point operations (FLOPs) is considered as the criterion of complexity. Moreover, only the complexity of channel estimation between single-transmit and single-receive antennas is given. For multi-antenna scenarios, it only needs to multiply by the number of transmitting and receiving antennas based on the single-antenna scenario.

Fig.2 shows the computational complexity caused by the initial estimation and offline training of different channel estimation methods. In Fig.2,N=128,Np=32,E=80,R=256,Q=4,L=5. From Table 1 and Fig.2, compared with the DL-based channel estimation, LS has lowest computational complexity. Since the two training processes (i.e., pre-training and training) are adopted and the input is too much in Ref.[7],its complexity is highest. Ref.[4] employed the DNN with two hidden layers and larger inputs, while the single hidden layer BP and basis coefficient estimation is used by the proposed method. Therefore, the proposed method has lower complexity compared with the schemes in Ref.[4] and Ref.[7].

Table 1 The comparison of computational complexity

where 2(LQ+Np) ＜4N.

Fig.2 The computational complexity contains initial estimation and offline training of different channel estimation methods

3 Simulation results

In this section, the simulation results are given for the proposed algorithm. The simulation parameters are given as: a MIMO-OFDM system has two transmitting antennas and two receiving antennas, the length of OFDM symbol is 128, and the number of pilots is 32.The carrier frequency is 2.35 GHz, and the subcarrier spacing is 15 kHz. The maximum mobile velocity is 500 km/h, and the Ricean channel with five paths is adopted, and Ricean factor is 5. In the simulation,the number of BEM coefficients is 4, the number of neurons in hidden layer is 80, and the network is trained with a range of signal noise ratio (SNR). Moreover,the LS with linear interpolation,the DNN-based scheme with two hidden layers in Ref.[4] and Ref.[7] are also simulated.

Fig.3 shows the mean square error (MSE) performance of the proposed method with different numbers of training samples. It can be seen from the Fig.3 that as the number of training samples increases, the estimation performance of the proposed method also improves. When the number of the training samples is larger than 2000, the estimation performance improves very little and tends to be stable.

Fig.3 MSE of proposed method with different numbers of samples

Table 2 shows the time required to train the network of the proposed method using different numbers of training samples. From Table 2, one can see that the more training samples,the more time is required to train the network, which means the computational complexity is higher. Therefore, the number of training samples should be a compromise between estimated performance and complexity in the practical. In following simulations, the number of training samples is set as 1000.

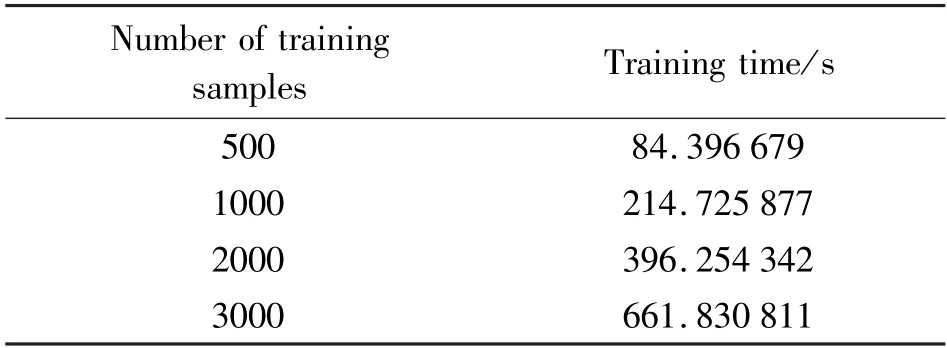
Table 2 Training time under different numbers of samples

Fig.4 gives the channel tracking curve by using different channel estimation methods, where SNR is 10 dB. Compared with LS estimator and Ref.[4], the Ref.[7] and the proposed estimator exhibit more accurate channel tracking. Fig.5 shows the MSE performance of different channel estimation methods. As shown in Fig.5, the DL-based estimation algorithms significantly outperform LS estimator. Since the historical channel estimation with estimation error is employed in Ref.[4], its MSE performance is worse than those of proposed method and Ref.[7], especially it has an error floor in the region of the high SNRs. Moreover, the performance of the proposed method is slightly worse than that of the Ref.[7], that is because Ref.[7]used the dual training processing and input more training sample parameters, such as the historical channel estimation,the received signal,and the current channel estimation, while the proposed method only uses one training processing and inputs the basis coefficient estimation of the current channel and the received pilot signal. In addition, as the SNR increases, the performance of the proposed method is getting closer to that of Ref.[7].

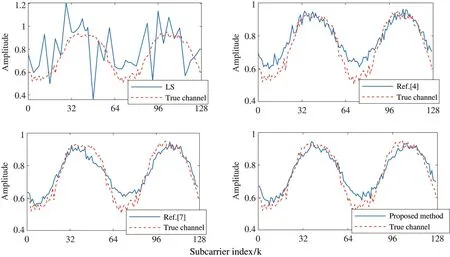
Fig.4 Channel tracking curve by using different channel estimation methods

Fig.5 MSE performance of different channel estimation methods

Fig.6 shows the MSE performance of different schemes under the different Doppler shifts, where SNR is 20 dB. It can be seen that the MSE performance will be deteriorated as the Doppler shift increases, but the DL-based schemes are still robust under the high Doppler shift. With the increase of Doppler shift, the proposed method has almost the same estimation performance as that in Ref.[7], especially the proposed method only uses little inputs.

Fig.6 MSE of different schemes under the different Doppler shifts

Fig.7 shows the MSE performance of proposed method with different training goals. In Fig.7, ‘true channel’ is the method adopts the true channel as the training goal in the training phase for the loss function,and ‘LMMSE estimated channel’ indicates that the estimated channel by LMMSE is used as the training goal in the training phase for the loss function. As shown in Fig.7, the proposed method still has a good performance when the LMMSE estimated channel is used as the training goal in the training phase.

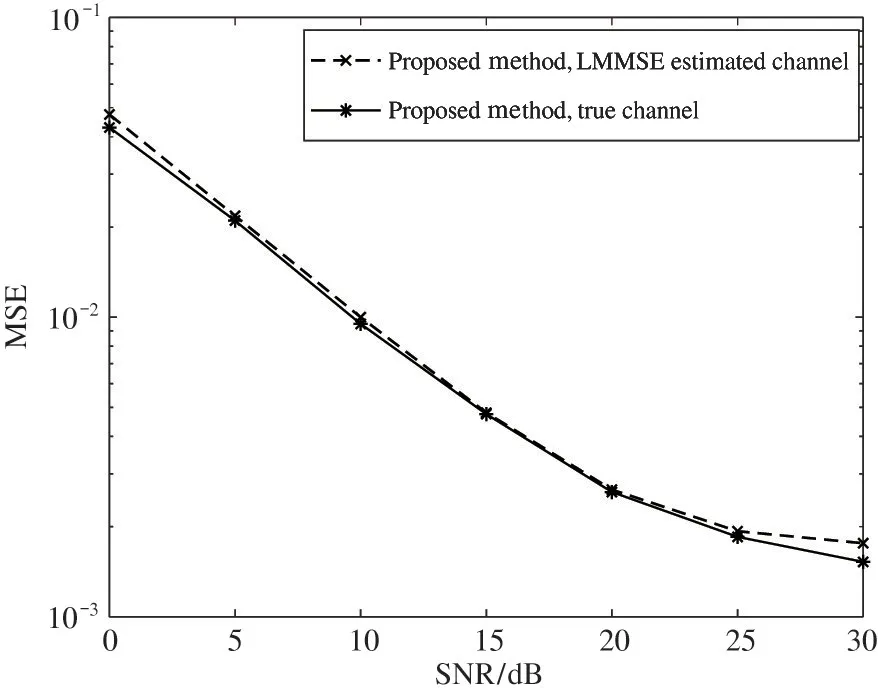
Fig.7 MSE performance of proposed method with different training goals

4 Conclusion

A DL-based time-varying channel estimator with BEM is designed for the MIMO-OFDM system. The proposed method not only has better performance, but also has low complexity. Moreover, the LMMSE estimated channel (not the true channel) is employed for the loss function in training phase, which makes the proposed method more practical.