新建建筑上跨施工对浅埋大断面隧道结构的安全影响研究

沈佳佳，万利，张长安，吴涛

(山东省交通规划设计院集团有限公司，山东 济南 250031)

在既有浅埋隧道上方新建建筑时，新建工程造成的附加荷载通过围岩传递至隧道结构，会导致原有下伏隧道结构受力增大，甚至影响既有隧道结构的服役安全。因此对于此类工程，除了需计算地基承载力外，还需要对附加荷载作用下既有隧道结构的安全性进行评估。目前，国内外针对附加荷载对隧道结构的影响研究多集中于城市地铁领域。魏新江等[1]利用Boussinesq 解求得在地面堆载时盾构隧道轴线处的附加应力，进而结合最小势能原理推导出了盾构隧道转动与错台变形公式。魏纲等[2-4]同样基于上述思路建立了基于“荷载—结构”法计算模型，提出了以椭圆度为指标的盾构隧道安全评估方法；建立了基于“地层—结构”法三维模型，分析了不同堆载大小和位置对盾构隧道变形的影响。刘庭金等[5]通过现场实测和数值计算研究了盾构隧道在地面堆/卸载作用下的受力与变形规律。姚爱军等[6]基于模型试验和数值模拟研究了在基坑开挖与加载作用下地层压力分布与盾构隧道变形特征。而对于浅埋大断面公路隧道，该领域的研究较少。事实上，相对于盾构隧道而言，钻爆法修建的浅埋大断面隧道，其衬砌结构形式存在显著的差异，盾构隧道常用的椭圆度、错台、转动等评价指标并不适用于复合式衬砌结构，而基于半无限弹性体假定的Boussinesq 解也同样不适用于浅埋大断面隧道围岩附加应力场的求解。除此之外，由于新建建筑上跨浅埋大断面公路隧道的边界条件复杂，采用理论方法固然难以给出附加应力的解析解，但采用数值计算也同样存在一些问题：1) 若单独采用“荷载—结构”模型，则存在隧道附加荷载不明确的问题；2) 若单独采用“地层—结构”模型，虽然规避了“荷载—结构”模型需要预先计算隧道附加荷载问题，然而由于“地层—结构”模型计算结果受围岩参数、隧道分部开挖应力释放过程、计算模型等众多因素的影响，其结构受力计算结果有可能较工程实际偏不安全[7]，因此也不宜单独将其结果作为工程设计校核的依据。鉴于上述问题，本文以青岛朝阳山生态文化公园综合服务建筑扩建工程为依托，提出在引入应力扩散原理的基础上综合“地层—结构”与“荷载—结构”2 种模型联合分析的思路(图1)：首先，运用“地层—结构”模型从应力扩散的角度研究在地表荷载作用下，附加应力的扩散规律以及应力扩散角范围；进一步，通过“荷载—结构”模型研究应力扩散角与隧道结构安全性能关系，最终得出较为准确的隧道受力评估结果，为类似工程提供参考。

1 工程概况

青岛朝阳山生态文化公园综合服务建筑扩建工程(以下简称“新建综合服务建筑”)位于原综合服务建筑西北侧，建筑面积3 600 m2，地上总体2层，局部4层，建筑主体部分均位于既有朝阳山隧道上方。朝阳山隧道为分离式双向6车道隧道，总体呈南北走向，左右线净距4.9～6.2 m，隧道内轮廓采用三心圆形式，净宽14.21 m，路面以上空间净高7.70 m，矢跨比0.54，最大开挖面积150.83 m2，属于小净距大断面公路隧道隧道段，如图2。

原综合服务建筑设置于隧道右线棚洞与明洞上方，采用柱下独立基础跨越棚洞结构两侧，建筑荷载通过柱下独立基础直接传递至棚洞下方基岩而不作用于棚洞与明洞，确保隧道结构安全；新建综合服务建筑毗邻原综合服务建筑，其主体结构上跨左线隧道明洞与Ⅴ级围岩浅埋暗挖段，采用筏板基础立于隧道拱腰上方地表，上部结构附加荷载通过筏板传递至围岩与隧道。

2 地层附加应力扩散规律

2.1 地层-结构模型

计算断面选取隧道结构受力最不利位置—小净距Ⅴ级围岩浅埋暗挖段，如图3。根据既有结构设计与计算资料，该断面位置地表建筑为4层，结构荷载通过框架柱传递至两侧筏板基础，筏板采用钢筋混凝土结构，沿隧道纵向平行布置，左右侧宽度分别为4.2 m 与3.8 m，高度0.7 m，通过上部结构计算得到计算段基底反力PKA与PKB分别为686 kPa 和710 kPa。隧道埋深5.2 m，隧道结构为复合式衬砌，初期支护为28 cm 厚C25 喷射混凝土，二次衬砌为60 cm 厚C30 模筑钢筋混凝土。地层主要为中风化花岗岩。相关参数如表1，表中喷射混凝土的材料参数为喷射混凝土与工字钢的等效参数。

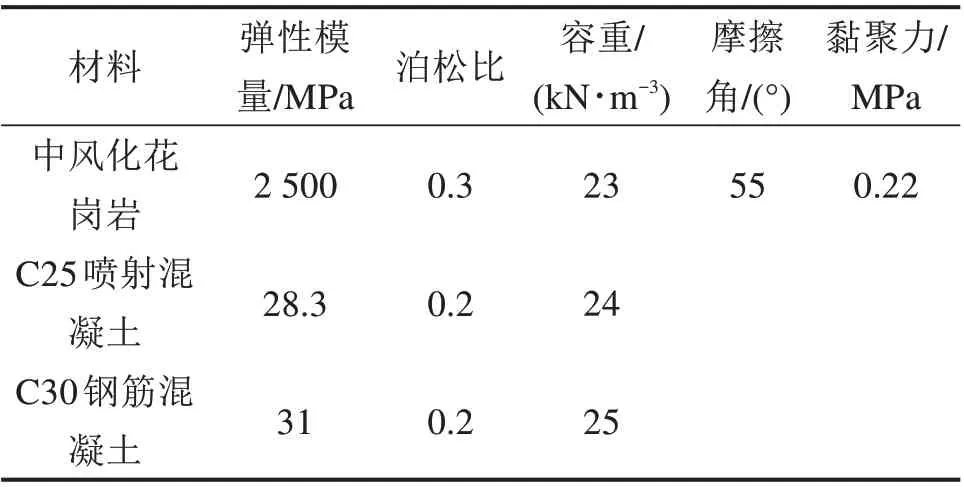
表1 力学计算参数Table 1 Mechanical parameters

有限元模型考虑隧道建设期CRD 法开挖的时空效应[8]，即在计算中，首先模拟隧道CRD工法开挖与支护过程，期间分步进行临空面的应力释放，实现围岩应力重分布，使隧道结构受力与围岩应力场更接近现场实际，再进行附加荷载的加载。隧道初期支护、临时支护与二次衬砌均采用梁单元模拟，初期支护与二次衬砌之间设置接触单元模拟初期支护与二次衬砌间的接触作用，围岩采用符合Drucker-Prager 屈服条件的平面应变单元模拟，如图4。

2.2 地层附加应力扩散角

图5为地表建筑荷载加载后其下方地层竖向附加应力云图。分析可知，建筑荷载产生的附加应力以竖向压应力为主，影响范围约从地表往下35 m 左右，受荷载水平与隧道约束影响，右侧附加应力影响范围较左侧稍深。

图6为附加主应力矢量图，表明附加应力在隧道周边无法自由扩散而形成切应力流，在拱肩、拱腰和拱脚部位局部应力集中，最小主应力值约为-318～-276 kPa，可见附加应力分布受隧道的影响较大。

在地表建筑基础下方2～22 m 深度范围内设置若干条水平测线，得出地层附加应力随深度的关系如图7。分析可见，除部分测线因穿越隧道内部空间而造成应力数据不连续外，地层附加应力总体上呈“W”型，即筏板基础正下方附加应力最大，沿基础两侧迅速减小，除却隧道附近围岩应力扰动区[9-10]，地层附加应力总体上呈现由浅到深峰值逐渐减小，范围逐渐扩大的趋势。以左线隧道中轴线为界，每侧附加应力分布均符合Gauss函数形态，因此可通过函数拟合[11]的方式求解应力扩散角。

构造附加应力分布函数：式中：a，μ，σ为拟合参数。

显然，式(1)可看作正态分布概率密度函数[12]，即X～N(μ,σ2)。因此，对结果样本只需选取[μ-2σ，μ+2σ]置信区间即可确保f(x)积分后包含不低于95%的附加荷载值，由此可计算应力扩散角[13]。

计算某深度影响范围内的平均附加应力PZ：

根据应力扩散法原理[14]，基底各深度的附加荷载相等，对于平面应变模型，则有：

式中：PK为建筑基底应力；d为建筑基底宽度；θ为附加应力扩散角。

联立式(2)和式(3)便可得出应力扩散角：

记Φ(x)为标准正态分布函数，式(4)可写为：

按式(5)计算得到附加应力扩散角如表2。分析可知，在隧道埋深范围内，其左右两侧附加应力扩散角∠α与∠β分别介于33.3°～37.0°与20.1°～27.8°，附加应力扩散角随深度的变化幅度较大，且计算位置据隧道越近附加应力扩散角越小，这主要是由于隧道周边围岩受应力集中效应的影响，竖向应力值大，造成计算的应力扩散角小。

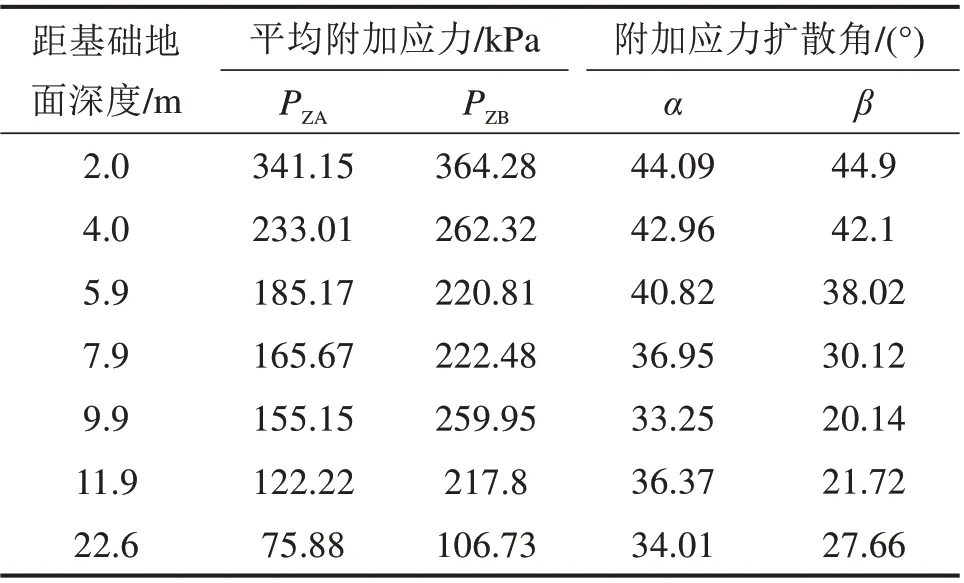
表2 附加应力扩散角计算结果Table 2 Computation of pressure diffusion angle

3 基于应力扩散的衬砌安全性分析

3.1 基于零阶优化算法的荷载-结构计算模型

以左线隧道为例，隧道二次衬砌采用梁单元模拟，围岩对结构作用采用受压弹簧模拟，弹性抗力系数150 MPa/m，外荷载取“围岩荷载+附加荷载”，其中围岩荷载采用直接加载方式，根据小净距隧道围岩压力计算方法，假定二次衬砌均承担80%外荷载作用[15-17]，得到左线隧道二次衬砌围岩压力如表3 与图8。附加荷载采用零阶优化算法迭代计算加载，结构最大计算裂缝宽度w与安全系数K按规范算法[15]计算。

表3 围岩压力Table 3 Pressure of surrounding rock

零阶优化是一种通过一定次数的抽样，拟合设计变量、状态变量与目标函数的响应函数从而求解最优解的方法，采用平方拟合的目标函数为[18]：

当设计变量与状态变量有约束条件时，可引入罚函数将目标函数转化为无约束最小值求解：

式中：xi为设计变量；ĝi，ĥi与ŵi为状态变量；f0为目标函数参考值；pk为响应面参数；X，G，H，W为罚函数，以X为例，其形式如下：

式 中：c1，c2，c3和c4为 系 数；xu与xl为xi的 上下限。

如图9，已知计算断面筏板基底反力PKA和PKB，将未知条件附加应力扩散角∠α及∠β视为设计变量，通过基底反力与设计变量按照应力扩散法原理按照式(3)计算隧道结构附加荷载，将结构最大计算裂缝宽度w定义为状态变量，将结构整体安全系数K定义为目标函数，从而建立起附加应力扩散角与衬砌结构安全系数之间的映射关系：

3.2 优化序列结果

经迭代计算，得到的优化序列结果如表4和图10。分析表明，衬砌结构安全性能与附加应力扩散角有密切关系，当左右基础下方附加应力扩散角基本一致时，左线隧道衬砌结构安全系数与最大裂缝宽度均表现为3个显著阶段。

表4 应力扩散角与结构安全性能关系Table 4 Relationship between pressure diffusion angle and safety effort of tunnel

1) 隧道安全系数：扩散角处于3°～17°，总体呈现较为稳定的下降段；17°～40°呈现平稳的水平段；大于40°时出现迅速下降的下降段。

2) 最大裂缝宽度：扩散角小于17°时，最大裂缝宽度由最大0.15 mm 逐渐减小到0；17°～29°维持0 mm 不变；大于29°时急剧上升，并在42°时裂缝宽度增大至0.2 mm，达到结构裂缝宽度限值。

3.3 安全极限范围

从一般角度考虑，将扩散角∠α与∠β均视为互不关联的独立变量，计算左线隧道结构安全系数、最大裂缝宽度随附加应力扩散角的变化如图11 和图12。结果表明：

1) 附加荷载的偏压情况对二次衬砌的承载能力有重要影响。左线隧道结构安全系数随应力扩散角的变化分为明显的3 个区域，当∠α与∠β差异较大时落于区域Ⅰ和区域Ⅱ，该区域内两侧附加荷载差异较大，偏压较严重，结构安全系数基本小于2.0，结构处于不安全状态；当∠α与∠β差异较小时落于区域Ⅲ，该区域内隧道两侧附加荷载大致相同，结构的安全系数均大于2.0，结构承载能力满足要求。此外，在区域Ⅲ内，安全系数总体随应力扩散角的减小而增大，且∠α与∠β基本相等时的方向即为安全系数的梯度方向，如图11 箭头方向。

2) 左线隧道二次衬砌最大裂缝宽度随应力扩散角的变化情况与安全系数类似，当扩散角位于最大裂缝宽度分布图左上角与右下角时(即左右两侧基础下方应力扩散角差异较大时)，裂缝宽度均大于正常使用状态下允许最大裂缝0.2 mm的限值；仅当扩散角分布在一定范围内时(图12 虚线区域)，裂缝宽度能够满足规范的限值[15]要求。

综上，存在一个安全区域，当应力扩散角大致 处 于α∈[6°，40°]，β∈[5°，40°]，α-β∈[-15°，20°]范围内时，附加荷载作用下的左线隧道结构能够满足安全运营的要求，根据“地层-结构”模型计算结果，应力扩散角位于安全区域内，因此可以认为综合服务建筑扩建工程的实施可以保证左线隧道运营安全。

同样运用上述分析方法对附加荷载作用下的右线隧道进行研究。结果表明，在单侧附加荷载作用下，右线隧道二次衬砌安全系数随着应力扩散角∠β的增大而逐渐减小，同时最大裂缝宽度逐渐增大，当∠β=28°时，二次衬砌安全系数为3.55，最大裂缝宽度为0.2 mm，结构达到正常使用状态下允许最大裂缝的限值，由“地层-结构”模型结果可知，隧道埋深范围内∠β介于20.1°～27.8°，因此综合服务建筑扩建工程的实施可保证右线隧道运营安全。

4 现场实施情况

为确保现场与计算模型吻合，避免出现超限的偏心作用，朝阳山生态文化公园综合服务建筑扩建工程按照对称方式施工，保持两侧筏基荷载基本一致严格控制基础荷载，并按照图13 所示在新建综合建筑影响范围内的隧道拱顶与两侧拱腰位置沿纵向布置了监测点，用于监测综合服务建筑施工期间隧道衬砌沉降变形，以计算断面为中心，整理得到施工完成后隧道最终沉降变形结果如图14。

监测结果表明，隧道沉降与附加荷载高度相关，计算断面与最大沉降位置基本重合，计算断面选择合理。左右线隧道最大沉降位置均位于左拱腰位置，最大沉降量分别为5.4 mm 与2.6 mm，数值上与∠α=36°，∠β=22°条件下相应位置的数值计算结果6.0 mm 与3.1 mm 较吻合，由此证明了在项目整个施工过程中，隧道处于安全稳定状态。目前，扩建工程已顺利完工并投入运营，新建综合服务建筑下方朝阳山隧道衬砌结构工作状态良好，无新增结构裂缝，隧道运营安全可靠，符合设计预期。

5 结论

1) 新建综合服务建筑基础下方附加应力扩散角随深度变化，扩散角∠α与∠β分别介于33.3°～44.1°与20.1°～44.9°之间，受朝阳山隧道围岩扰动区的影响，波动范围较大，表现为接近隧道位置的扩散角较小，远离隧道位置的扩散角较大。

2) 附加荷载的变化引发朝阳山隧道安全性变化，直观表现为隧道安全系数与最大裂缝宽度随应力扩散角变化，存在一个安全区域，即当应力扩 散 角 大 致 处 于α∈[6°，40°]，β∈[5°，28°]，α-β∈[-15°，20°]范围时，可确保朝阳山左右线隧道二次衬砌安全系数均大于2.0，最大裂缝宽度均小于0.2 mm，满足结构安全运营要求。

3) 结合“地层—结构”模型得出的隧道两侧附加应力扩散角的范围和“荷载—结构”模型得出的隧道安全性能与附加应力扩散角之间的关系，推断出朝阳山隧道两侧附加应力扩散角处于安全区域内，综合服务建筑工程实施后朝阳山隧道可安全运营。施工期间监控量测结果表明，隧道衬砌工作状态良好，实际变形量与计算结果较吻合，验证了计算方法的合理性与可靠性。

4) 提出了一种以应力扩散原理为基础，结合数值计算的方法研究了新建建筑对下方浅埋大断面隧道安全性能的影响，其分析过程清晰、结果可靠，有力指导了设计与施工，为类似工程的实施提供了参考。