基于航迹运行模式的航空器航迹优化模型

李萌，初建宇，李印凤,2，苗亚，傅航，傅子涛

(1. 华北理工大学 建筑工程学院，河北 唐山 063210；2. 中国电子科技集团第二十八研究所 空中交通管理系统与技术国家重点实验室，江苏 南京 210007；3. 中国民用航空局空中交通管理局 运行管理中心，北京 100022；4. 中国民用航空华北地区空中交通管理局 通信网络中心，北京 100621)

随着世界各国对航空运输需求的与日俱增，现行的空中交通管理模式和有限的空域资源已经不能满足航空业高速发展的要求。航班延误及空域拥堵等问题时有发生，威胁空中交通运行安全。为突破当前空管系统所处的瓶颈，在新一代空管系统中提出了基于四维航迹运行(Trajectory Based Operation，TBO)这一核心理念。TBO 是以安全、精准的管控航空器的运行为目的，参考并在空管系统内共享航空器的四维航迹(4 Dimensional Trajectory，4DT)，实现各参与方间的协同决策。四维航迹是指在航空器整个起降过程中经历的所有点的四维坐标(时间和空间)的集合[1]。TBO 是国际民航组织最新发布的全球航行计划中航行系统组块升级的总目标，也符合我国民航局空管局下发的中国民航空中交通管理现代化战略和四强空管行动方案，满足民航业提升空管运行保障能力的需求。国内外学者针对TBO 模式下的四维航迹规划,从不同角度出发展开了积极探索。DOUGUI 等[2]为了生成无冲突的4D 轨迹集，引入了一种新的光传播算法。RUIZ 等[3]提出了运用关系空间数据结构和时空数据结构的概念，进行轨迹与路径之间的战略冲突检测。SOLER等[4]研究了轨迹转换敏感环境中的4D 轨迹规划问题，建立了四维航迹的混合整数最优控制模型。YAN 等[5]以安全有效分配4D轨迹为目的，研究了全网范围的4D 飞行轨迹规划问题。GUAN 等[6]以减少总延误和航空器的冲突数量为双目标，建立航迹优化模型，并采用进化算法求解。QIAN 等[7]在减少燃油成本和延误成本的基础上，考虑安全距离的约束，建立航空器无冲突的四维航迹优化模型，并设计最大改进分布式算法求解。DAL 等[8]以最短延误和最小费用为目标，结合空域用户的偏好，建立了多目标二进制整数编码的四维航迹优化模型。SAITO 等[9]从分散航班轨迹来实现噪声公平分配的角度，提出了两阶段航迹规划方法。DAL 等[10]考虑利益相关者的偏好和延误航班重新排序的优先级等约束，建立了多目标四维航迹规划模型，并用模拟退火算法求出帕累托解。AHMED 等[11]使用3 次样条逼近方法，将四维航迹规划模型的目标函数和约束条件表示为时间节点的状态和控制值的函数。SEENIVASAN 等[12]通过设置风暴空域的飞行约束，并结合运行限制，建立了航空器航迹规划模型，并采用混合最优控制解决问题。TIAN 等[13]从绿色空管的角度出发，以常规成本和温室气体及有害气体等环保因素成本为目标，设计了四维航迹的绿色规划模型，并采用A*搜索算法和梯形并置方法来优化四维航迹。韩云祥[14]对单航空器和多航空器的航迹进行了系统规划。公言会[15]通过栅格法和元细胞自动机建立了航路网络优化模型并求解。周娟[16]从启用临时航线的角度出发得到最优航线。张阳等[17]通过改变过关键点的时间和高度，对预战术阶段的多空域航迹进行规划。何德暘[18]建立了基于飞行计划集中处理的预战术阶段航空器航迹规划理论。陈雨童等[19]以航路运行为对象，开展了面向受限空域的自主航迹规划与冲突管理技术研究。在航迹规划方面，现有研究成果主要从航路分配及微观冲突探测等方面展开研究。为满足空域扇区内的飞行需求，本文以达到扇区内的整体容流平衡为目的，以时效性和经济性为优化目标，构建基于四维航迹运行的航空器航迹规划模型，并设计带先验种群的双染色体NSGA-Ⅱ遗传算法求解。

1 巡航阶段航迹规划模型

1.1 建模思路

空域或机场容量是指空域和机场在特定时间内可接收的最大飞机数量[20]。扇区内的航路点、航路及其容量构成了带权重的空中交通网络有向图，综合反映交通流的组成及空域限制信息。空中交通网络如图1 所示，其中，p 为航路点，R 为航路，f 为流量，c 为容量。繁忙空域扇区内的流量与容量失衡问题不仅造成了空中交通网络的拥堵，还威胁着扇区内航空器的飞行安全。针对扇区内流量过大造成的空域拥堵，本文从平衡扇区容流的角度出发，兼顾时效性与经济性，以各个航空器的进、出扇时间作为决策变量，以总延误时长最小及总油耗量最少为优化目标，构建宏观层面的航空器四维航迹双目标规划模型，为航空器规划进、出扇区时间，减少各航空器之间的冲突，保障扇区容流平衡。

1.2 基本假设

基于扇区复杂的空域结构及运行情况，为简明、全面的描述问题，建立以下假设：

1) 将航空器看作一个质点，处于巡航状态；

2) 各航空器按原定计划时间进扇；

3) 上游、下游扇区均处于容流平衡状态；

4) 不考虑航空器在一个扇区内的速度改变；

5) 不考虑扇区内已有航空器。

1.3 模型参数

模型中的符号及其定义如表1所示。

表1 模型中符号定义Table 1 Symbol definition in the model

1.4 双目标优化模型

模型的目标函数及约束条件如式(1)～(7)所示：

目标函数式(1)为时间成本目标f1，表示进扇区总延误时长最短；目标函数式(2)为经济成本目标f2，表示总燃油消耗量最小，以保证不同机型的航空器在飞行过程中的油耗成本；式(3)表示扇区内容量与流量平衡约束，即在时间段Ti内，扇区S内的流量需小于等于容量，且大于等于容量的μ倍(μ为常数，μ＜1)，方可在不浪费空域资源的同时保障航空器飞行安全；式(4)和式(5)分别表示进、出扇时间间隔约束，即对于进、出扇航路点相同的航空器，进、出扇区时间需满足最小时间间隔，以减少航空器间冲突，fm+1是与fm进、出扇航路点相同的相邻航班；式(6)表示不提前进扇约束，即航空器fa规划后的进扇区时间不能早于计划进扇区时间；式(7)表示扇区内飞行时长约束，航空器fa在扇区正常飞行时有tda=taa+la/va，而规划后因采取调整措施，形成扇区内消耗时长Δt，即t′da=t′aa+la/va+Δt，则扇区内飞行时长Δt′=la/va+Δt，故为保障运行安全及效率，需约束航空器在扇区内的飞行时长。

1.5 模型求解

相较于基本遗传算法，多目标遗传算法更适用于解决多个目标函数在给定解空间上的优化问题。基于本文提出的双目标航迹规划模型，选用快速非支配遗传算法(NSGA-Ⅱ)进行求解。图2 为遗传算法求解流程。

为了更好地抑制早熟，提高算法的运行速度及搜索精度，本文使用更加符合生物特性的二倍体双链染色体结构并添加先验种群，算法中的遗传操作如下。

1) 编码方式

因问题搜索空间大且约束条件复杂，本文选用实值编码方案。研究中把各个航空器的进扇、出扇时间换算成相较于当天00:00:00的时间差，并计算为分钟，以此实值表示一个基因。另外，因问题决策变量个数较多，故以双链染色体表示一个个体，其中，一条染色体表示进扇区时间，另一条则表示出扇区时间。例如，若问题中有5架航班，它们的进扇区时间分别为08:00:00，08:06:00，08:10:00，08:15:00和08:04:00，出扇区时间分别为08:10:00，08:16:00，08:20:00，08:25:00和08:14:00，则采用实值编码的二倍体双链染色体基因型如图3所示。

2) 遗传算子

本问题为多染色体的多目标优化问题，因此选用锦标赛选择算子、模拟二进制交叉算子和多项式变异算子来进行遗传操作。

2 实例分析

2.1 算法运行结果

根据华北区域2018 年10 月历史飞行计划数据，统计分析了各扇区流量，最终以2018 年10 月28日ACC05扇区的繁忙时段16:00:00～16:29:59的飞行计划数据为基础进行预处理，预处理步骤包括：1) 在飞行计划数据中，筛选出计划进入ACC05 扇区的航班信息；2) 清洗掉进扇和出扇时间相同的航班信息；3) 统计扇区日流量，选择繁忙、有容流冲突的时段；4) 确定航班机型、进扇区点等模型所需要的数据。

利用python 进行编程，实现带先验种群的双染色体NSGA-Ⅱ算法。扇区半小时内的容量设定为23 架次。ACC05 扇区结构如图4 所示，其中主要航路有7 条，主要进扇区航路点有3 个，分别为ISGOD，LARAD-B458-UBTAB和ENGIL。部分飞行计划数据如表2所示。

表2 部分飞行计划数据Table 2 Partial flight plan data sheet

遗传算法中设置最大进化代数为500，种群规模为60。算法进化的帕累托解集如图5所示。

图5 中，F1 为航空器流进扇区延误时长，F2为航空器流在扇区内飞行时的燃油消耗量，F1 进扇区延误总时长的最优解集在94～121之间；F2总燃油消耗量的最优解集在11 682～12 783 之间。根据式(1)和式(2)，进扇区延误时间越长，规划后进扇区时间越晚，即t′aa的值越大，则(t′da-t′aa)的值越小，即F1与F2之间具有相互抑制作用，F1值得到优化的同时F2 值的优化程度会减小。帕累托最优解是使F1 和F2 尽可能达到最优的解的集合。模型最终得出多种兼顾时效性与经济性且符合约束条件的航迹优化策略，使决策者可结合实际情况对2个目标函数值进行比重加权，选择较为适当的航迹规划方案。表3列出了从帕累托最优解集中选取的9种优化方案。

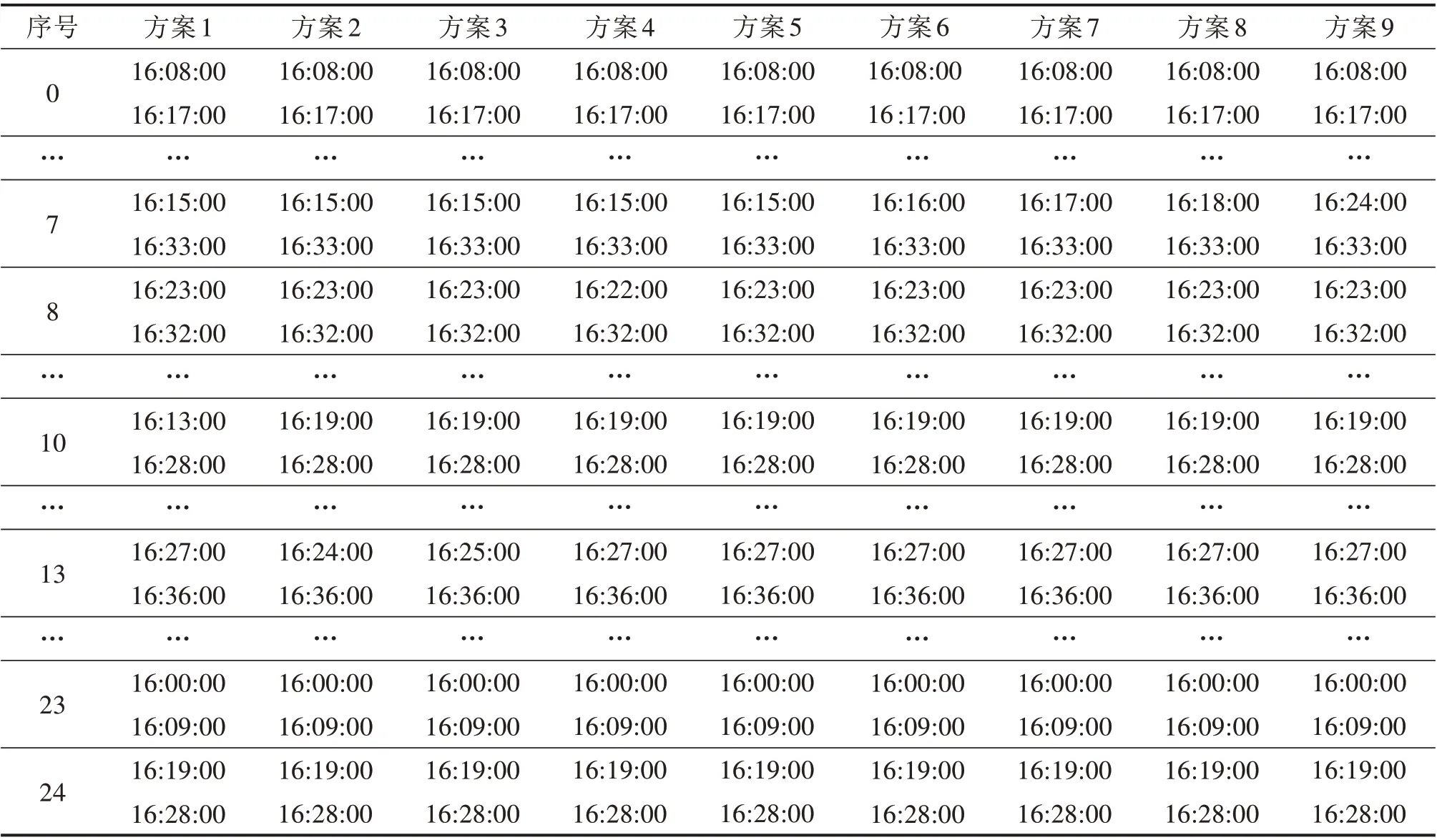
表3 进、出扇区时间优化方案Table 3 Optimization scheme of inbound and outbound sector time

2.2 算法比较

为了验证本算法的运行速度及优化效果，分别与差分进化算法、基本遗传算法、单目标双染色体基本遗传算法和不加先验种群的双染色体NSGA-Ⅱ算法进行了对比，其中，差分进化算法、基本遗传算法和单目标双染色体基本遗传算法的参数设置如表4所示。本文算法与对比算法的进化结果如表5和图6所示。

表4 对比算法参数设置Table 4 Compare algorithm parameter settings

从表5 和图6 可以看出，在优化效果上，本文算法的进扇区延误时长较差分遗传算法、基本遗传算法和单目标双染色体基本遗传算法分别平均降低了45.47%，57.77%和61.13%，燃油消耗较差分遗传算法、基本遗传算法和单目标双染色体基本遗传算法分别平均降低了37.19%，31.27%和2.49%，且差分遗传算法与基本遗传算法因自身局限性，均产生局部收敛过快的现象。在计算速度上，本文算法较无先验种群的双染色体NSGA-Ⅱ算法提升了56.58%。综上所述，本文采用的带先验种群的双染色体NSGA-Ⅱ算法在优化效果及运算速度方面都优于其他算法，可在较短的时间内提供多种较优的扇区内航空器航迹规划策略，具有灵活性和适用性，降低了扇区内的航空器冲突风险，实现了空域资源合理分配及充分利用。

表5 本文算法与无先验种群的双染色体NSGA-Ⅱ算法运行速度对比Table 5 Running speed of the proposed algorithm is compared with that of the two-chromosome NSGA-Ⅱalgorithm without prior population

3 结论

1) 改进的快速非支配遗传算法在优化程度和计算效率方面得到明显的提升，目标优化效果方面，改进的快速非支配遗传算法较差分遗传算法、基本遗传算法和单目标双染色体基本遗传算法平均提升了39.22%，且改进算法收敛稳定，不易陷入局部最优解；计算效率方面，改进的快速非支配遗传算法较无先验种群的双染色体NSGA-Ⅱ算法提升了56.58%。

2) 提出的模型可以在较短的时间内给出较优的策略，使航空器进扇区延误总时长和扇区飞行的燃油消耗总量均达到了较优的水平，给决策者提供满足其不同偏好的调整方案，符合空中交通管理过程中的实际管制需求。