基于下加载理论的土料广义塑性本构模型

张 博，朱 晟

(1.山东电力工程咨询院有限公司，山东 济南 250013；2.河海大学水工结构研究所，江苏 南京 210098)

0 引言

很多试验资料表明[1-2]，土料加卸载过程中都会产生塑性变形，并且加卸载过程中会产生一个闭合的滞回圈。为模拟这种与常规塑性理论框架不同的变形，Hashiguchi[3-5]提出了“下加载理论”。下加载理论包括2个嵌套的屈服面，即当前屈服面和参考屈服面，或称为下加载面和正常固结面。该理论在提出以来被广泛地用来改进常规的弹塑性模型，如Yao等[6]将下加载概念用于统一硬化模型描述超固结土的力学性能，这个模型也可以用来模拟循环加载下的土体行为。

Zienkiewice等[7-8]提出了土体的广义塑性理论，该理论直接定义塑性流动方向张量、加卸载方向张量及塑性模量来构建本构矩阵，并且可以较容易地反映出土的剪胀性、循环荷载变形累积性。由于该理论概念清晰且便于编程实现，近年来在土工领域的应用越来越广泛。在高土石坝的应用中，邹德高等[9]对P-Z模型进行改进，并应用于实际工程；陈生水等[10-11]基于广义塑性理论建立了可以考虑颗粒破碎和循环荷载变形特性的堆石料的广义塑性本构模型；朱晟等[12]根据高坝室内三轴试验，并结合广义塑性理论推导了可反映防渗土料和堆石料的统一广义塑性本构模型。

本文基于广义塑性理论框架，结合下加载理论，推导一个可以反映土料在复杂加卸载条件下的本构模型。

1 广义塑性理论基础

广义塑性理论中总应变增量及弹性应变增量满足如下关系：

(1)

塑性势函数为g(σ)=0，在加载过程中的塑性应变增量的方向可以通过下式确定：

(2)

式中，dλ是标量因子。

加载过程中，应力必须满足屈服面方程f(σ，h)=0：

(3)

式中，h为硬化参数，控制屈服面的大小及位置，此处假设其为εp的标量函数。

将式(1)和式(2)带入式(3)，得：

(4)

将式(2)及(4)带入(1)中第3式可得：

(5)

式(5)方括号中给出了弹塑性劲度张量Dep的一般表达式，即：

(6)

其中

(7)

式中，ng为塑性流动方向张量，nf为加载方向张量，H为塑性模量。

将式(2)、式(7)带入式(3)可得：

(8)

故式(2)可改写为：

(9)

由式(1)及式(9)可得广义塑性本构方程的柔度形式：

(10)

其中，Cep称为弹塑性柔度张量。

根据式(10)可以得出三轴应力状态下体积应变增量dεv、剪切应变增量dεs与平均应力增量dp、剪应力增量dq的关系：

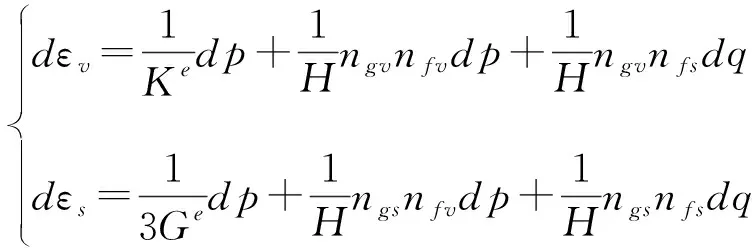
(11)

式中，Ke和Ge分别为弹性体积模量和弹性剪切模量；ngv和ngs是ng的分量；nfv和nfs是nf的分量。

2 应力应变特性

2.1 弹性变形特性

类似于剑桥模型，土体的弹性模量可以通过e-lnp图得到：

(12)

式中，κ为等向回弹线的斜率，e0为p=p0对应的初始孔隙比，ν为泊松比，一般可取值为0.3。

2.2 塑性流动方向向量

采用Lagioia[13]改进的剪胀方程：

(13)

式中，Mc为土体剪缩到剪胀转换时的应力比，η为应力比，μ不等于1。图1为Fujinomori黏土的剪胀方程，可见式(13)可以较好反映土料的剪胀规律。

图1 剪胀方程

不考虑应力主轴旋转时，塑性应变增量为：

(14)

塑性应变增量的模为：

(15)

将式(14)(15)带入式(7)中，并结合式(2)，可得塑性流动方向ng的表达式：

(16)

2.3 加载方向向量

2.3.1 加载方向的定义

采用非相关联流动法则，加载方向的定义与塑性流动方向类似，可直接用下式表示：

(17)

其中，df的定义如下：

(18)

2.3.2 强度特性

1)参考屈服面和当前屈服面。参考屈服面为正常固结状态下土料所对应的屈服面。在复杂加卸载条件下的土料的当前应力点相当于正常固结状态的应力点依照某种“映射法则”对应的超固结状态的应力点，其所在的屈服面称之为当前屈服面。当前屈服面与参考屈服面的形状相似，如图2所示。

图2 当前屈服面和参考屈服面

对式(18)积分可以得到参考屈服面表达式：

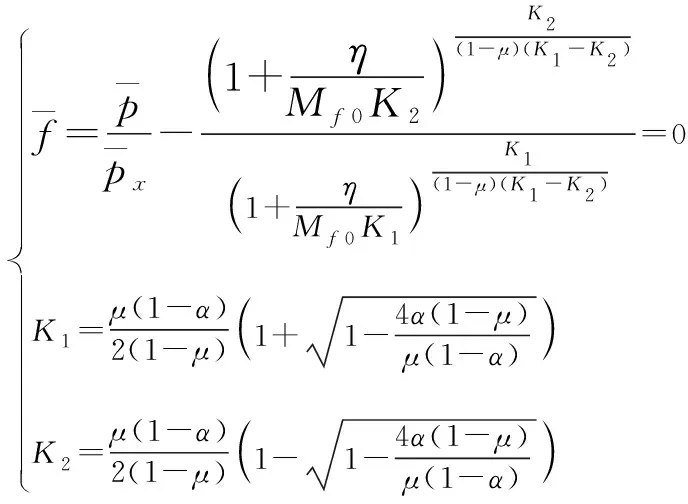
(19)

式中，Mf0为正常固结状态下土料的初始破坏应力比。

(20)

式中，κ为回弹再加荷曲线的斜率，λ为加荷曲线的斜率，e0为初始孔隙比，p0为等向压缩条件下p的初始值。

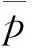
(21)

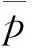
(22)

3)破坏应力比。随着复杂荷载的施加，正常固结土将变为超固结土，即本次循环荷载施加时的土体相对于首次施加荷载时表现为超固结土的变形性质。在多次加卸载过程中，土体逐渐密实，其破坏应力比也会相应增大。类似于超固结土，在复杂加卸载条件下的破坏比Mf的推导中引入伏斯列夫线(见图3)，可推得破坏时qf的表达式：

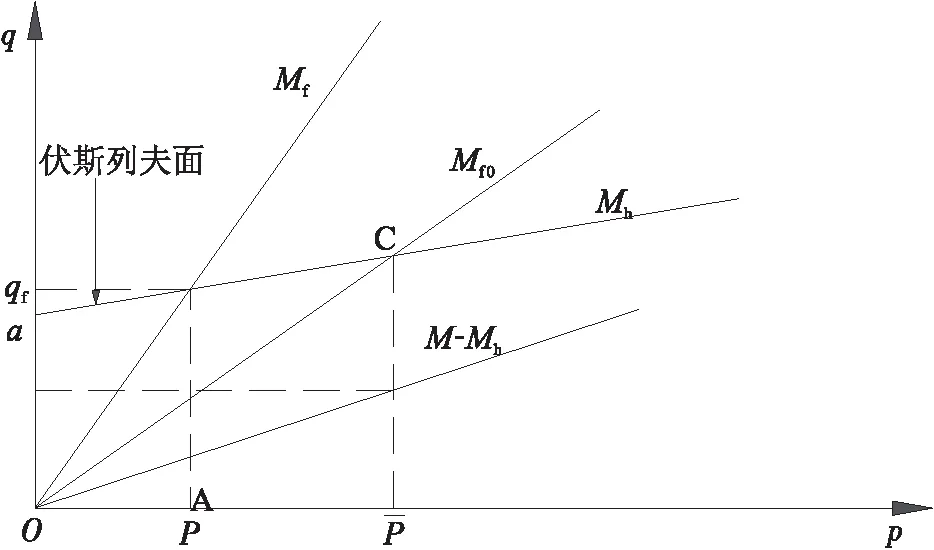
图3 破坏强度推导

(23)

由式(23)可得破坏比如下:

(24)

式中，Mh为伏斯列夫线的斜率。考察式(24)，当不受复杂荷载时R=1，破坏比Mf即为初始破坏比Mf0。

2.4 塑性模量

2.4.1 等向压缩条件

土体等向压缩条件下q=dq=0，带入式(11)第一式可得:

(25)

对土体等向固结试验结果式(9)微分可得(等向固结应力路径在子午面上沿p轴，此处用p代表px):

(26)

结合式(25)和式(26)可得等向压缩条件下土料的塑性模量如下:

(27)

由式(27)可知，等向压缩时土体塑性模量随平均应力增加而增加，体现了土体的压硬性。

2.4.2 恒压剪切条件

式(27)中塑性模量只反映了平均主应力的影响，但在恒压剪切条件下，试样的塑性模量一直减小并最终等于零。因此，考虑剪应力的影响，应将式(27)乘以一个随应力比η增大而从1减小至0的函数。参考相关文献，并通过大量的假定和试算后，本文定义的塑性模量如下：

(28)

式中，d为一个无量纲的参数，可以通过拟合三轴压缩试验资料，采用IGA反演确定。当η=0时，式(28)退化为等向压缩时的塑性模量式(27)；当η=Mf时，塑性模量H=0，塑性变形可以一直增加，最终材料破坏，此时意味着土体达到流动破坏。

2.5 加卸载准则

在常规弹塑性理论中，加卸载准则借助屈服面来确定，不能够考虑材料的记忆功能，只能用于单一加卸载应力路径而不能应用于复杂加载条件。

在本文中采用下述判断准则：

(29)

当η<ηm且dη>0时存在2种情况

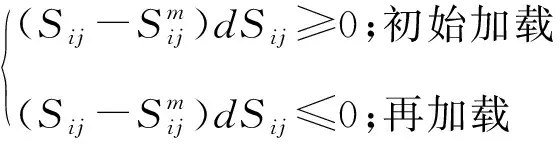
(30)

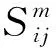
2.6 模型三维化

上面公式只适用于三轴压缩和等向压缩应力状态，不能用于一般应力状态。本模型针对黏土料提出，并且所采用的子午面上的破坏函数依然为线性函数，因此可以采用基于SMP准则[14]的变换应力法将上述本构模型推广到一般应力状态。

3 模型的验证

结合Fujinomori黏土三轴试验结果验证本文模型的合理性。

模型参数λ、κ、e0、Mh、Mf0、Mc可以通过三轴压缩试验和等向压缩试验获得，参数d可以通过IGA反演三轴压缩试验获得。Fujinomori黏土本构参数如表1所示。

表1 黏土本构参数

图4为平均主应力为196 kPa下单一加载条件下三轴压缩试验和三轴伸长试验结果与模型预测的对比图。图5和图6为复杂加卸载条件下试验结果与模型预测值的对比图。其中图5为平均主应力为392 kPa的等幅循环荷载，图6为平均主应力为196 kPa的不等幅循环荷载。由图5～6可知，在复杂荷载作用下每次加卸循环所产生的应变逐渐减小，应力应变关系曲线也随之逐渐加密。在循环荷载作用过程中，压缩曲线距离正常固结线越来越远，相当于超固结程度逐渐增大，使得超固结参数逐渐变小。通过对比2图的(c)图可知，循环次数较少时，R增加或减少的变化幅度较大，随着循环次数越来越多，R的变化幅值减小并逐渐稳定。

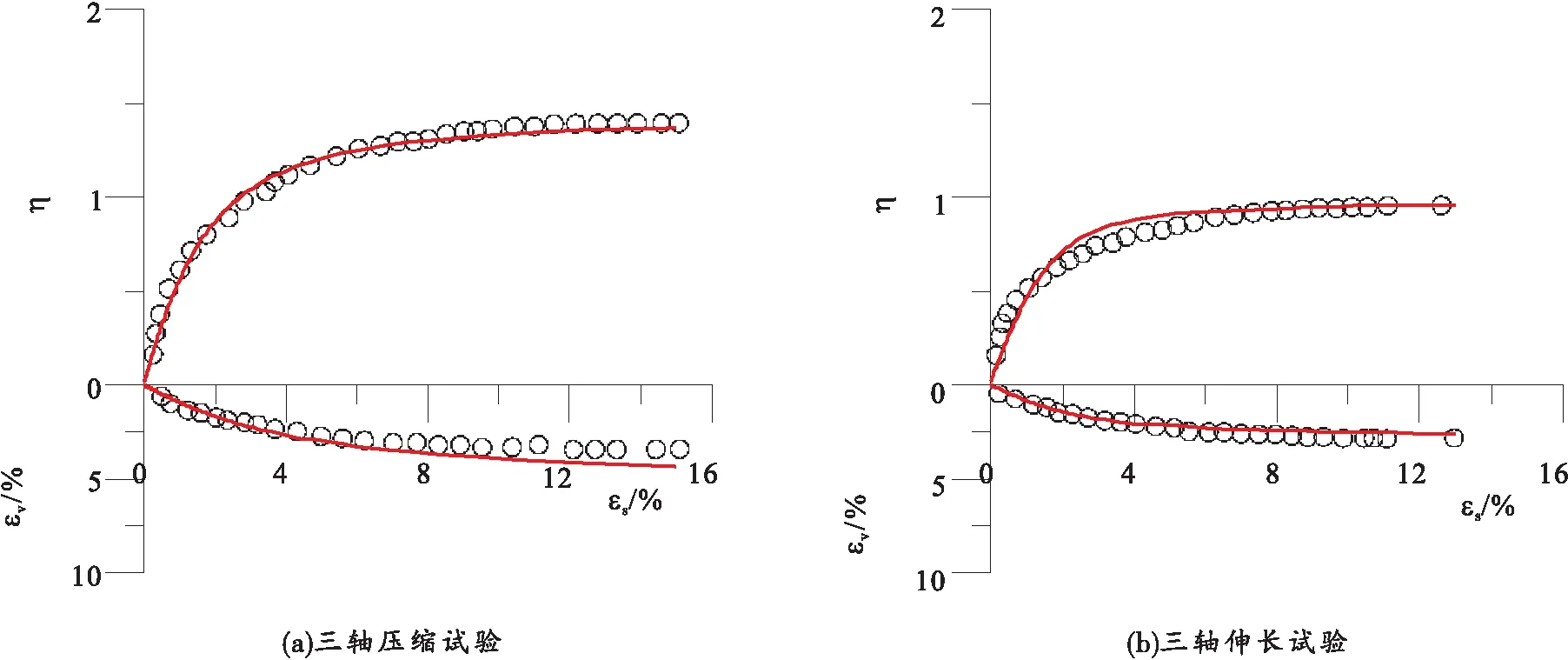
图4 单一加载条件试验结果与模型预测对比图

图5 等幅循环荷载试验结果和模型预测对比图

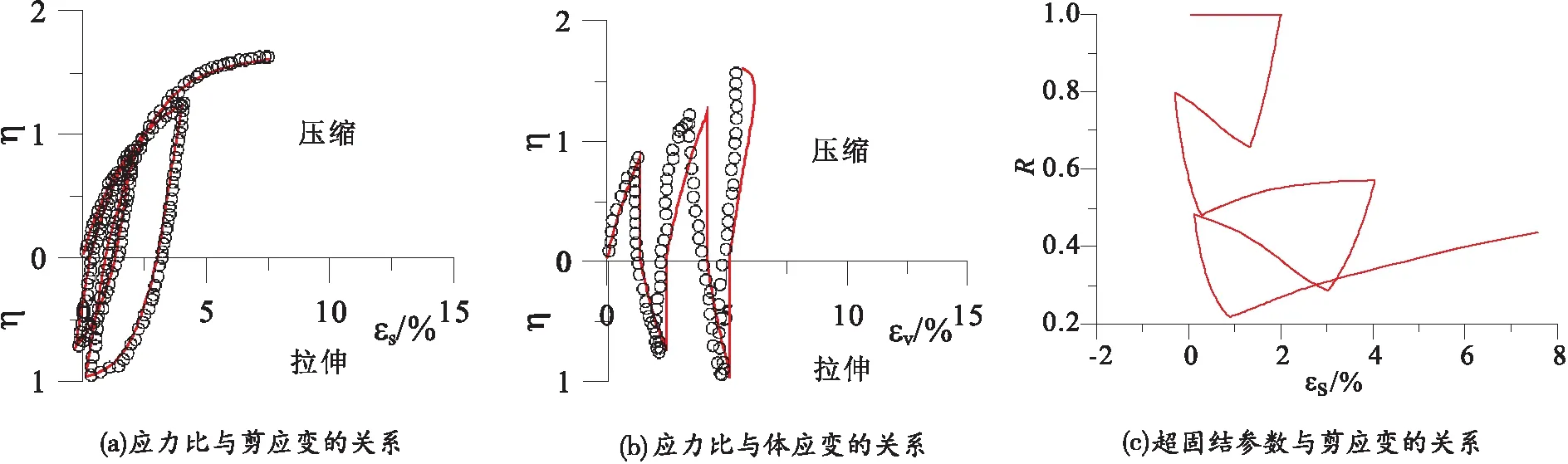
图6 不等幅循环荷载试验结果和模型预测对比图

由图4～6可知，本文提出的本构模型预测值与试验结果吻合较好。

4 结论

1)基于下加载理论的广义塑性本构模型既可以预测单一加载条件下土料的应力应变关系，也可以较好地预测复杂加卸载条件下的应力应变关系。

2)基于下加载理论，引入参考屈服面，推导了一个可反映应力历史及材料硬化行为的超固结参数。

3)该模型在广义塑性理论框架下无需推导当前应力点所对应的屈服函数，仅通过定义塑性流动方向向量、加载方向向量和塑性模量实现当前状态的模拟，使得本构建模工作具有极大的灵活性，并且该种方法也易于编程实现。