齿轮传递误差及其振动激励分析与仿真

李斯端

(德先汽车科技(上海)有限公司重庆分公司，重庆 401120)

0 引言

齿轮传动系统作为一种多自由度的弹性机械系统，系统上的振动激励源可分为外部激励和内部激励2大类，外部激励主要由驱动电机电磁谐波激励、负载扭矩波动和齿轮旋转质量不平衡、几何偏心以及系统中其他零部件的激励构成。内部激励是齿轮传动不同于其他机械结构的地方，它是由于齿轮啮合刚度和负载的交替变化引起轮齿弹性变形周期变化、齿轮传递误差等引起了啮合过程中啮入啮出冲击和速度载荷周期性波动，形成激励振动，因而即使没有外部激励，齿轮系统也会受到内部的动态激励而产生振动噪声。

齿轮传动系统的内部激励包含刚度激励、传递误差激励和啮合冲击激励3种形式。刚度激励是齿轮副在啮合过程中，由于单、双齿啮合的交替，齿轮副的啮合综合刚度在单对齿和双对齿之间周期性地交替突变，且在不同的啮合位置，每一对啮合轮齿的瞬时啮合刚度都不相同。在啮合综合刚度的作用下，齿轮的传递误差也产生周期性的波动变化，由于轮齿不断地重复啮合，传递误差的波动变化就形成了一种周期性的位移激励，导致齿轮传动系统产生振动和噪声。

本文以渐开线直齿轮为研究对象，对齿轮啮合综合刚度和传递误差进行分析和理论计算，同时运用Romax软件对直齿轮副进行建模、静力学分析和精确仿真与有限元分析，得到直齿轮副的啮合刚度和传递误差，与理论计算的结果对比具有较好的一致性，同时运用Romax软件仿真分析得出传递误差激起的振动时域波形和各阶次频谱图，为进一步的齿轮修形设计和振动噪声控制打下了良好的基础。

1 轮齿刚度激励

本文以1对圆柱直齿轮传动为例对齿轮的传递误差及振动激励进行分析，直齿轮副参数见表1。直齿轮副在Romax软件中的3D模型如图1所示。

表1 直齿轮副参数

图1 直齿轮副3D模型

轮齿刚度指的是1 mm齿宽上为使1对或多对同时啮合的无误差轮齿沿啮合线产生1 μm变形所必需的载荷。直齿轮的单对齿啮合刚度c’指的是一对轮齿接触的最大刚度，近似等于单齿啮合状态下一对轮齿的最大刚度。斜齿轮的c’指的是1对轮齿在法向截面内的最大刚度。啮合刚度cγ指的是啮合中所有轮齿刚度的平均值[1]。轮齿啮合综合刚度cm是指在整个啮合区(图2中的A～D段)中，参与啮合的各对轮齿的综合效应，其值等于参与啮合的各对轮齿的啮合刚度的叠加[2]。

对于圆柱直齿轮副，重合度一般为1～2，啮合接触点从有效齿廓起始点A(SAP)开始沿着啮合线逐步移动至有效齿廓终止点D(EAP)，如图2所示。在单齿啮合区B～C段，此时是1对轮齿参与啮合，齿轮的啮合综合刚度较小，综合弹性变形较大；在双齿啮合区A～B段和C～D段，此时是2对轮齿参与啮合，啮合综合刚度为2对轮齿综合刚度的叠加，综合弹性变形较小。可以看出，啮合综合刚度在整个啮合区是动态变化，具有明显的阶跃型突变性质。当重合度不同时，啮合综合刚度分布曲线将具有不同的形式；当重合度为整数时，啮合综合刚度的变化较小，基本不存在阶跃型突变[2]。

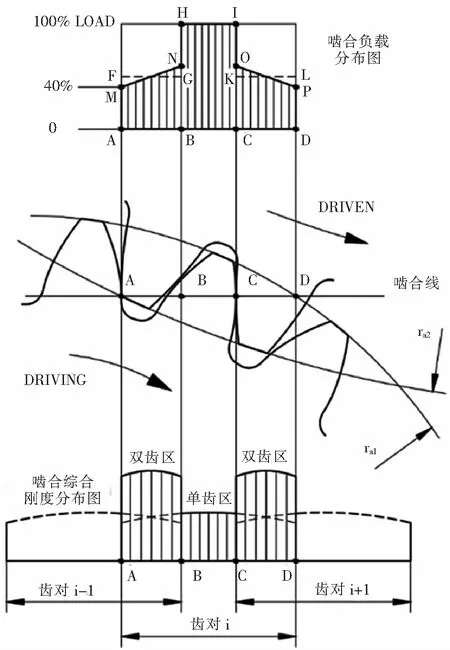
图2 啮合负载分布图

在单齿啮合区，轮齿啮合综合刚度cm等于啮合刚度cγ，即cm=cγ；在双齿啮合区，轮齿啮合综合刚度cm计算式为：

cm=c’+cγ

(1)

依据GB/T 3480.1-2019计算出的直齿轮副的单对齿啮合刚度c’和啮合刚度cγ以及啮合综合刚度如表2所示。

表2 直齿轮副理论啮合刚度 单位：N/mm·μm

通过Romax软件对直齿轮副的啮合刚度进行仿真分析，得出直齿轮副啮合时各接触点的瞬时刚度数据，如图3所示。直齿轮副的啮合综合刚度数据，如表3所示。

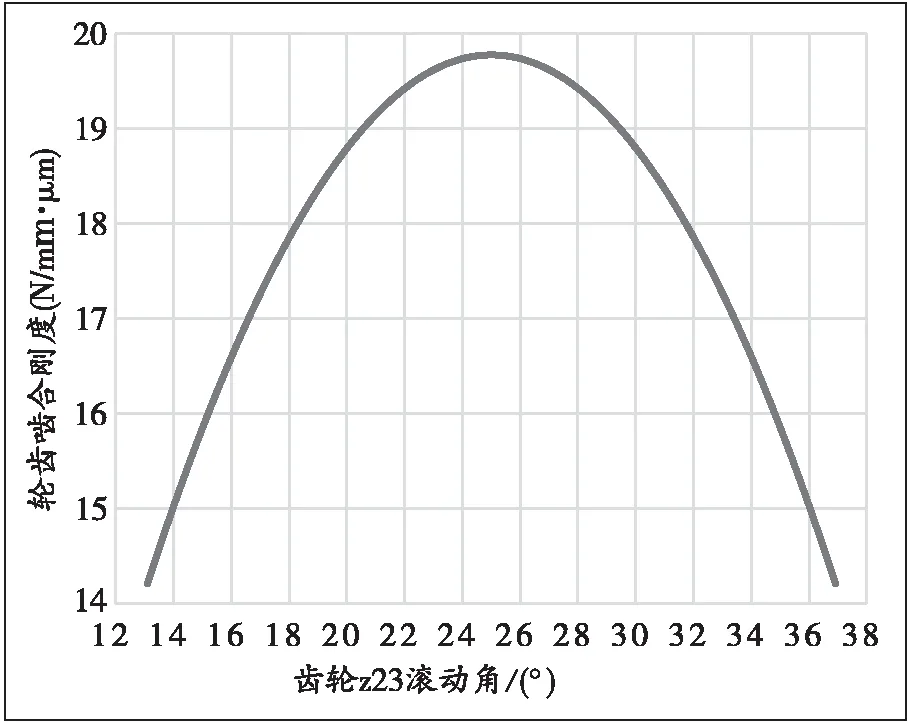
图3 直齿轮副瞬时啮合刚度分布图

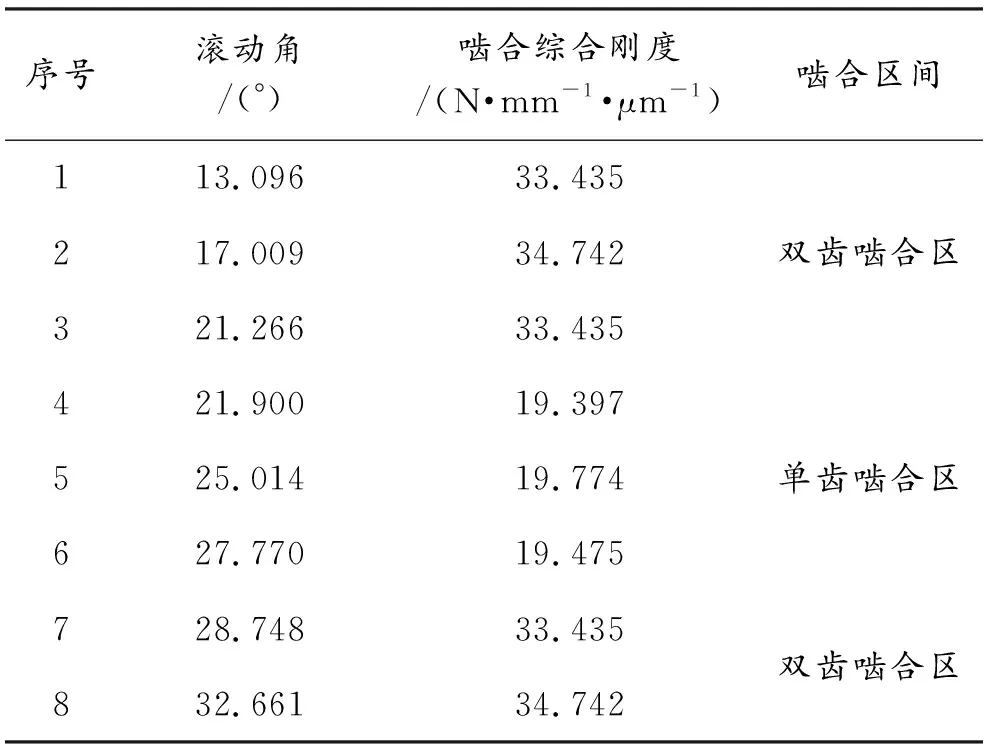
表3 直齿轮副啮合综合刚度数据

另一方面，在齿轮副啮合过程中，由于单、双齿啮合的交替，双对齿啮合区域A～B段和C～D段每对轮齿承担的负载约为单对齿啮合区域B～C段的40%～60%，但是承担的总负载始终保持不变。通过计算可得出负载的实际分布情况如图2所示[3]。齿轮啮合时沿啮合线(齿廓法向)的单位长度载荷按下式计算：

ω=Fn/b=Ft/b×1/cosαt

(2)

其中：Fn为沿啮合线作用于齿廓法向的作用力，N；Ft为分度圆上名义端面切向载荷，Ft=2M×1 000/d，N；M为齿轮所传递的扭矩，N·m；d为齿轮节圆直径，mm；b为啮合齿宽，mm；αt为齿轮端面啮合角deg。

通过上式计算得出直齿轮副的理论单位长度载荷为286.11 N/mm。

通过Romax软件仿真分析得出直齿轮副啮合时每对轮齿的单位长度载荷分布情况如表4和图4所示。总的理论单位长度载荷为286.11 N/mm，与前述理论计算结果完全一致。

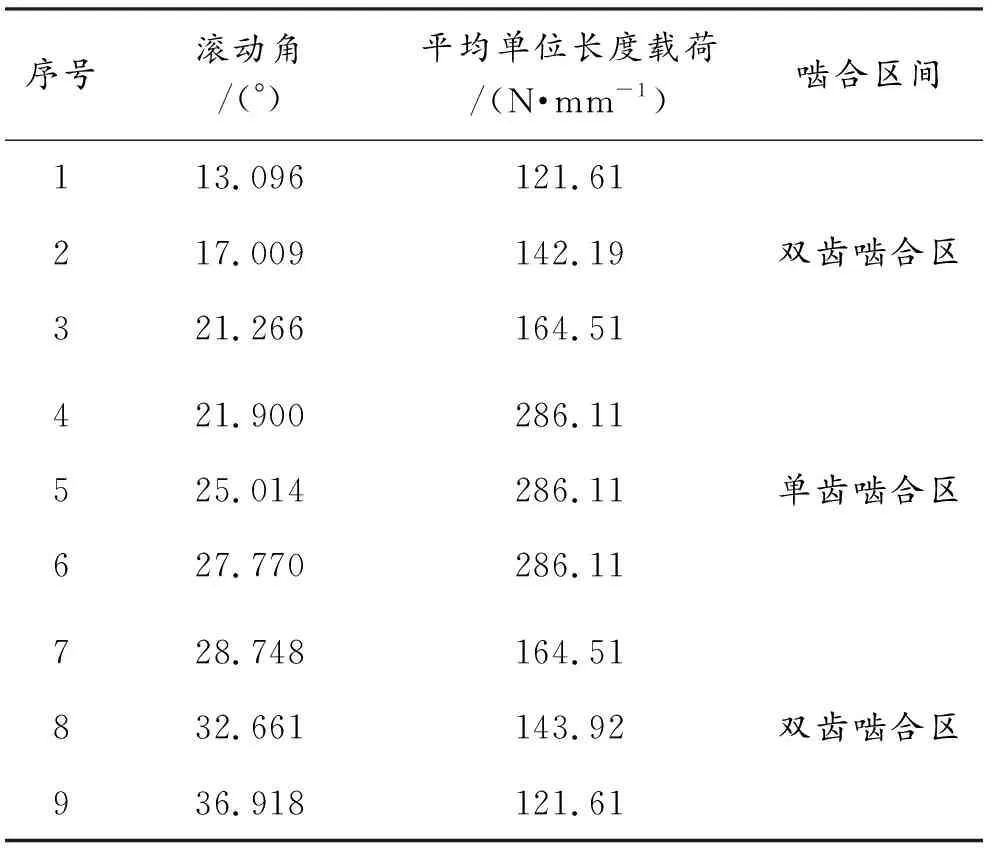
表4 直齿轮副单位长度载荷数据表

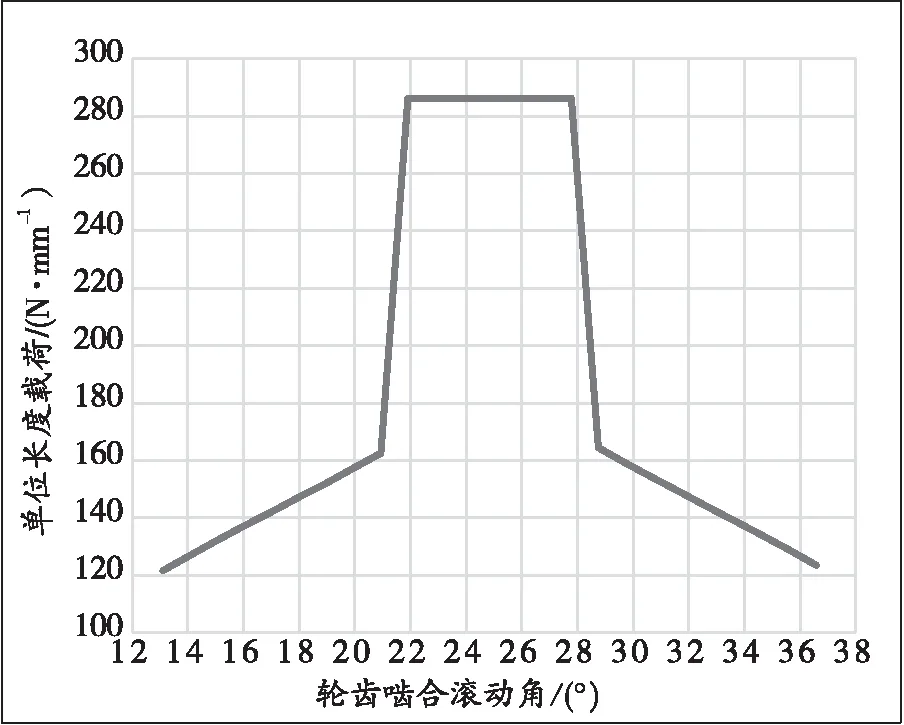
图4 直齿轮副单位长度载荷分布图

通过上述分析可知，直齿轮副在啮合过程中，轮齿啮合综合刚度和负载随着单、双齿啮合的交替进行而产生周期性的阶跃型突变，从而引起轮齿综合弹性变形周期性的交替突变，导致齿轮副角速度周期性的往复变化，对齿轮传动系统产生动态冲击激励，导致齿轮传动时产生振动和噪声。

对于斜齿轮传动，总重合度通常大于2，参与啮合的齿轮对数始终有2对以上，保证2对轮齿完全啮合的情况下啮入端轮齿从齿端逐步进入啮合，啮出端轮齿从另一齿端逐步退出啮合，啮合过程的轮齿交替是平滑过渡的，啮合综合刚度cm基本等于啮合刚度cγ，变化幅度很小，避免了直齿轮传动时的阶跃型突变。不过齿轮轮齿作为弹性体，其瞬时啮合刚度随着啮合部位的变化会产生细微变化，导致轮齿综合弹性变形在其啮合周期内产生细微波动变化，同样会引起啮合过程的动态刚度激励，不过其激起的振动幅值相较于直齿轮大幅降低。

2 传递误差激励

传递误差作为齿轮传动系统的内在激励，是由齿轮啮合本身产生的，其来源主要是齿轮制造误差和轮齿综合弹性变形。齿轮制造误差属于大周期误差，称为制造传递误差，其激励频率等于齿轮的转频，而轮齿综合弹性变形是由于轮齿接触部位的表面挤压变形和轮齿本身受载产生剪切、弯曲变形等多重因素造成，负载较大时其变形量往往是齿形误差的2～3倍，称为设计传递误差，其激励频率等于齿轮的啮合频率。传递误差TE主要由设计传递误差TEδ(φ)和制造传递误差TEΔ(φ)构成。

TE(φ)=TEδ(φ)+TEΔ(φ)

(3)

齿轮制造误差总会存在，通过设计限定齿轮的精度等级可使齿轮制造误差处于允许的设计范围内，齿轮精度等级越高，制造误差就越小，不过齿轮精度也不能无限制提高，一是因为制造误差并不是传递误差的主要构成因素；二是因为齿轮的加工成本会随着精度等级的提高呈几何级增加。汽车变速器的齿轮通常采用淬硬处理加磨齿加工，经济精度一般为5～6级。制造误差中对齿轮传动平稳性影响较大的主要是齿廓形状偏差ffα和基圆齿距偏差fpb，其他的可忽略不计。齿轮的齿廓形状偏差和齿距偏差在齿轮加工好后就是定值，基本不会因为其他因素的影响而发生改变，啮合齿轮的齿廓形状偏差和齿距偏差都是随机变量，且分别服从正态分布和差值分析，一般不会同时达到极限偏差，因此制造传递误差TEΔ在设计阶段按下式经验公式计算：

TEΔ=fpb+1/3ffα

(4)

其中：ffα为齿廓形状偏差，μm；fpb为基圆齿距偏差，μm。

轮齿弹性变形受轮齿刚度及其时变特性、载荷大小影响。一般来说，齿轮同时参与啮合的轮齿对数是周期性变化的，即齿轮的重合度不为整数。而轮齿作为一个弹性体将随载荷产生弯曲变形和接触变形，可以将啮合的轮齿简化为沿啮合线方向的时变弹簧，这样轮齿的刚度和变形随接触线位置发生周期性的变化。同时，轮齿啮合时，发生线接触，随着载荷的变化，接触线宽度也随之变化，进而导致变形随之变化(非线性)。设计传递误差为轮齿在啮合点处沿啮合线(齿廓法向)方向的位移，其计算公式为：

TEδ=ω/cm=(Ft/b×1/cosαt)×1/cm

(5)

式中：ω为齿轮啮合线上的单位长度载荷N/mm；cm为啮合综合刚度N/mm·μm。

通过上式计算得出直齿轮副的设计传递误差TEδ见表5。

表5 直齿轮副的理论设计传递误差 单位：μm

通过Romax软件仿真分析得出直齿轮副单对轮齿啮合周期内的设计传递误差TEδ(见表6和图5)，双齿啮合时轮齿的设计传递误差TEδ约为单齿啮合时的50%～60%。

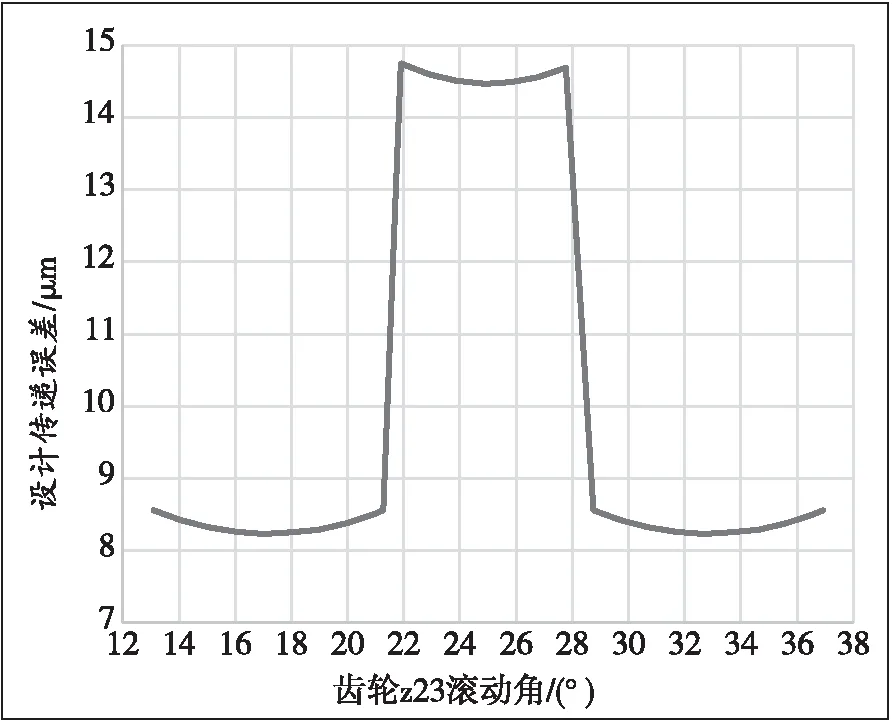
图5 直齿轮副设计传递误差TEδ分布图

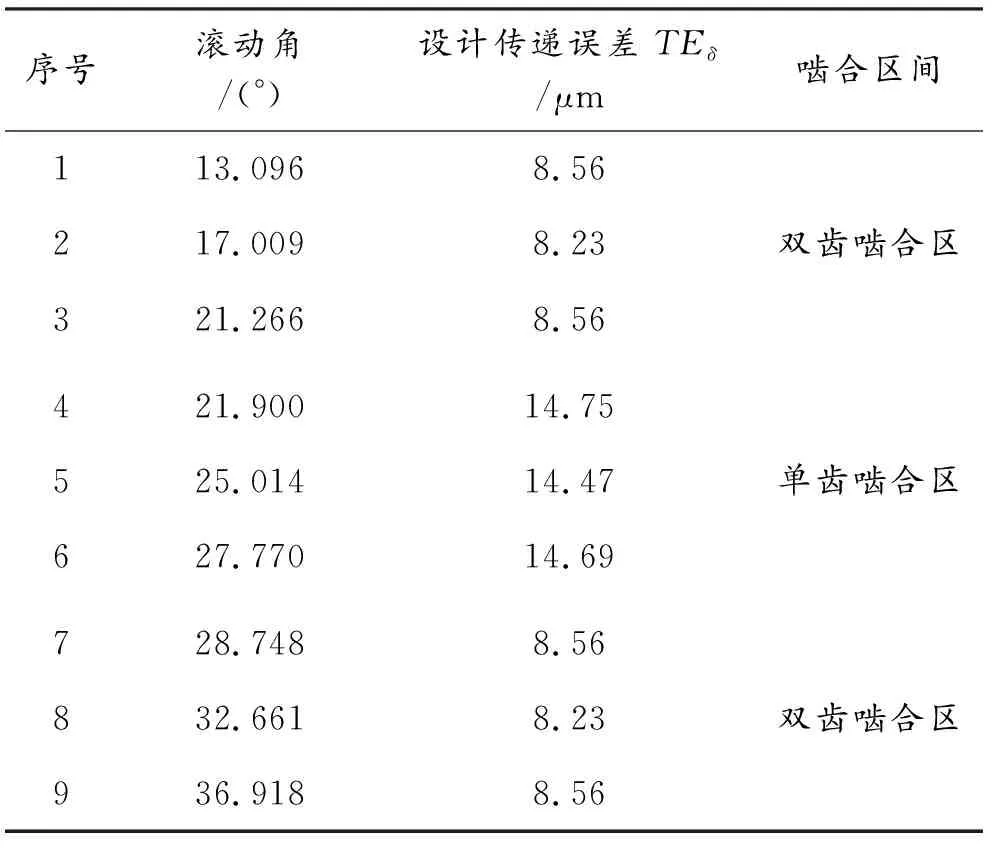
表6 直齿轮副设计传递误差TEδ数据

齿轮传动时啮合综合刚度和负载随着单、双齿啮合的交替进行而产生交替变化，造成齿轮的传递误差也在单、双齿啮合区间内波动变化，由于轮齿不断地重复啮合，传递误差的波动变化就形成了一种周期性的位移振动激励。

通过Romax软件仿真分析得出直齿轮副啮合时的静态位移变动时域波形(见图6)，其大周期波形为方波，主要是设计传递误差随着单、双齿啮合的交替进行而产生交替变化引起的周期性位移激励；其小周期波形为全波余弦波形，主要是齿形误差及轮齿综合弹性变形在其啮合区内因啮合部位的变化而产生的周期性小幅度位移激励引起的。由方波的傅里叶变换可知，频率成分包含奇数倍的高次谐波；由周期全波余弦信号的傅里叶变换可知，它的频率成分包含偶数倍的高次谐波[4]。通过快速傅里叶变换得到各阶次谐波的频谱图(见图7)，其中基频(一阶)振动频率为460 Hz，等于直齿轮副的啮合频率，其振动位移幅值为3.93 μm。当基于传递误差的任一谐波频率与减速器的某一固有频率相同或非常接近时，就会产生共振，从而发生啸叫。从图7可以看出，前三阶振动幅度较大，在后续的齿轮修形设计时要减小设计传递误差的波动范围以降低振动幅度，同时在减速器的结构和参数设计时要避免在前三阶产生共振。

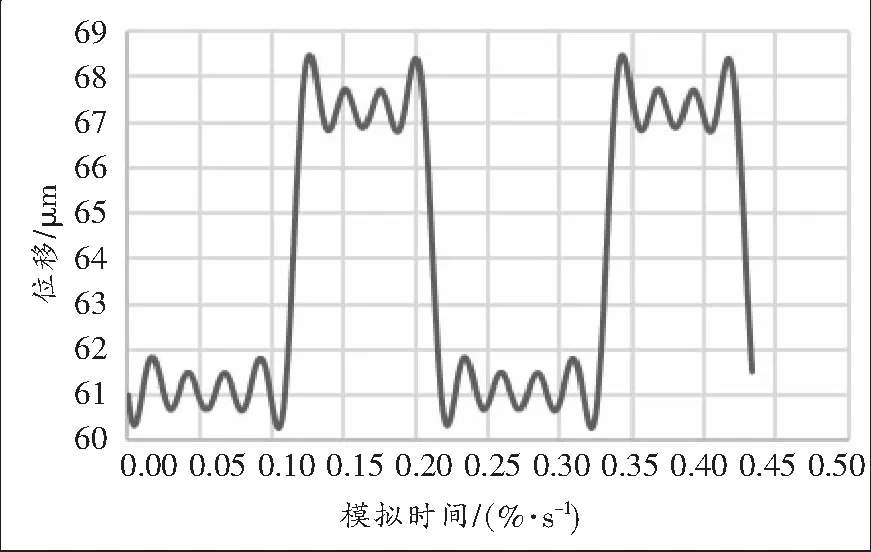
图6 静态位移变动时域波形图

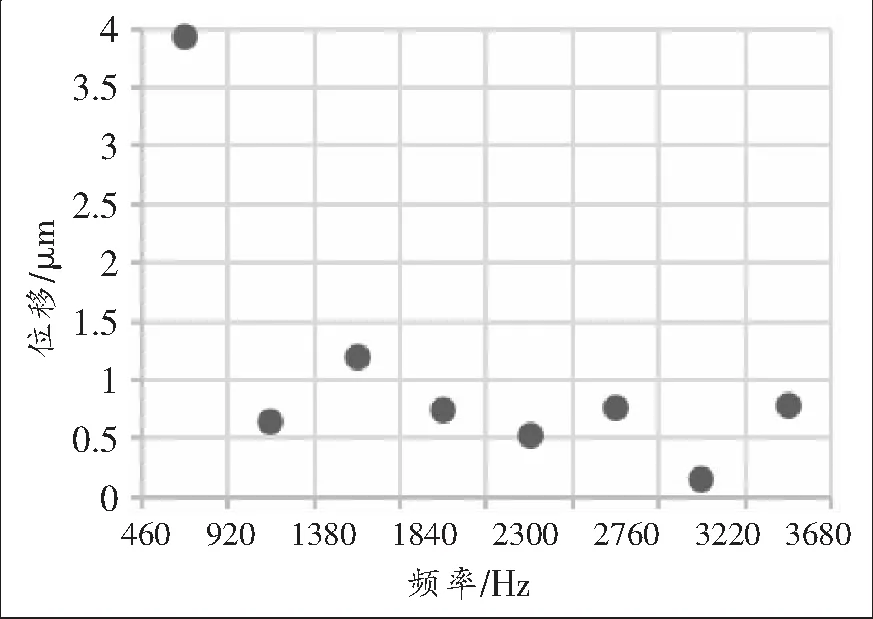
图7 各阶次谐诐频谱图

3 结论

1)本文通过理论分析和计算得出了直齿轮副的啮合综合刚度和传递误差数据，和Romax仿真分析的结果对比具有较高的一致性。单齿啮合区间的轮齿啮合综合刚度为双齿啮合时的50%～60%，单齿啮合区间的传递误差为双齿啮合时的160%～170%。轮齿啮合综合刚度随着单、双齿啮合的交替进行而产生周期性的阶跃型突变，引起传递误差周期性的波动变化。

2)啮合综合刚度cm是参与啮合的各对轮齿的综合效应，其值等于参与啮合的各对轮齿的啮合刚度的叠加。对于直齿轮副，在单齿啮合区，轮齿啮合综合刚度cm等于啮合刚度cγ，即cm=cγ；在双齿啮合区，轮齿啮合综合刚度cm=c’+cγ；对于斜齿轮副，轮齿啮合综合刚度cm=cγ。

3)传递误差TE由制造传递误差TEΔ和设计传递误差TEδ组成。制造传递误差TEΔ属于大周期误差，其激励频率等于齿轮的转频，引起的振动频率较低，一般远小于减速器的固有频率。设计传递误差TEδ的激励频率等于齿轮的啮合频率，引起的振动频率较高，各阶次频率与减速器的固有频率有较宽的重叠范围，可能引起齿轮传动系统发生共振，轮齿综合变形量越大其振动幅值就越高，振动烈度就越强，是影响传递误差的关键因素。

4)传递误差TE的周期性波动变化对齿轮传动系统产生周期性的位移振动激励，通过Romax软件仿真分析得出传递误差激起的振动时域波形和各阶次谐波的频谱图。当任一谐波频率与减速器的某一固有频率相同或接近时，就会使齿轮传动系统产生共振，从而发生啸叫。传递误差TE是影响齿轮啮合性能的主要因素，以及引起齿轮传动系统振动和噪声的根本原因。