滑移线教学中粗糙平冲头压入半无限体的非Prandtl解探讨1)

梅瑞斌 包 立 刘相华

*(东北大学材料与科学工程学院，沈阳 110819)

†(东北大学秦皇岛分校，河北秦皇岛 066004)

滑移线法作为金属塑性力学分析的主要方法之一，主要适用于理想刚塑性材料的平面应变问题，在一定条件下可以推导分析平面应力和轴对称以及硬化材料问题，不仅在力学分析中有较为广泛的应用[1-4]，更是高校塑性力学教材内容中的主要组成部分。关于粗糙平冲头压入半无限体这一经典力学问题，相关教材均基于Prandtl滑移线场，通过刚性三角形ABC在y向受力平衡的求解方法（如图1所示）分析接触面AB的平均单位压力，但该方法求解结论与光滑平冲头结果完全一样，在光滑和最大摩擦两种条件下接触面单位压力均为剪切屈服强度的5.14倍[5]，可见，Prandtl场未能准确反映粗糙接触面滑移线应力边值问题，计算结果也没有准确反映出金属塑性变形规律，给滑移线应用的课堂教学和学生理解带来了较大困扰。文献[6]给出了另外一种滑移线场，速度场也符合金属流动规律，但该场的两族滑移线在AB面中心点处重合而没有垂直，不符合滑移线相互正交原则。为此，本文基于Prandtl场理念和滑移线场应力边值特征，在研究文献的基础上构建了一种符合金属流动应力边界和滑移线性质的滑移线场，求解并分析了摩擦对接触面应力分布的影响规律，为学生理解滑移线性质和滑移线理论研究及应用奠定了理论基础。

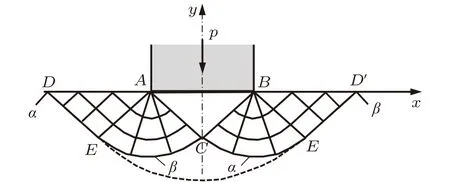
图1 粗糙平冲头压入半无限体Prandtl滑移线场

1 非Prandtl滑移线场构建

当塑性加工过程中工件与工具间出现全黏着现象时，一般认为此时接触表面上的摩擦应力为最大，即τk=k，根据应力莫尔圆描述的应力状态表达式可知，滑移线与接触表面的夹角φk为零或-π/2 。α线与β线应根据接触表面剪应力τk的正负指向情况来确定，如图2所示。

图2 黏着接触表面滑移线特点

根据黏着接触面的应力边界滑移线特征，参照光滑平冲头压入半无限体的Hill滑移线场和粗糙平冲头压入半无限体的Prandtl滑移线场，构建了新的滑移线场，如图3所示。关于该滑移线场的构建思路和解释如下。

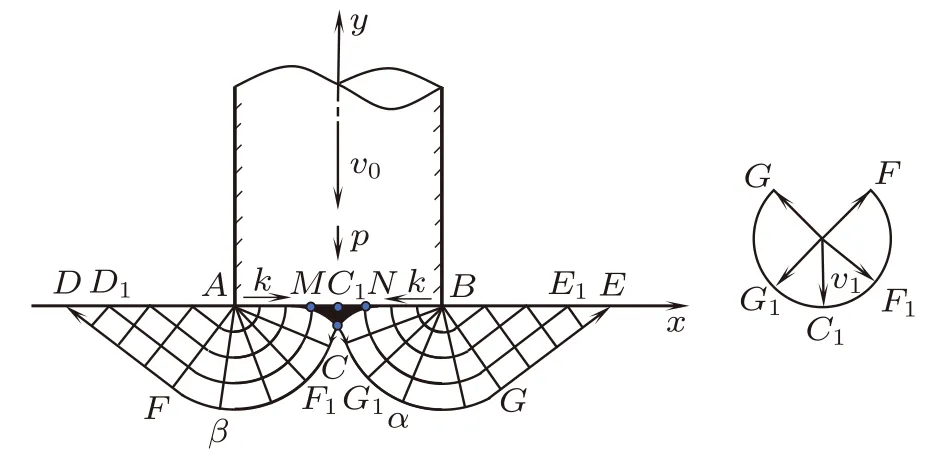
图3 粗糙平冲头压入半无限体滑移线非Prandtl场及速端图

（1）接触面为最大黏着接触摩擦，AM和BN线为最大剪切面，即为滑移线，符合最大摩擦条件的应力边值特征，AM两侧剪应力为顺时针，BN两侧剪应力为逆时针，根据规则AM为α线、MD1为β线，与AM垂直；BN为β线、NE1为α线，与BN垂直。

（2）由于冲头足够粗糙，与Prandtl场类似，中心非常小区域可近似为刚性等腰三角形MNC，MN为特殊边界，MC与NC从AB线弧形过渡到C点，C1点为中心对称点，并不发生x方向变形（对称中心，无摩擦存在），C点为速度不连续点，M、N和C非常接近C1点，α线AM的延长线（MC）与β线BN的延长线（NC）相交于C点并相互垂直。

（3）同无摩擦情况下Hill场一样，在自由表面上的塑性区也应是均匀应力状态的直线场AFD和BGE，边界滑移线与表面成45°角。

（4）由于流动的对称性，从冲头接触面引出的滑移线必须与AFD和BGE直线滑移线场连接，并与接触面呈90°，根据滑移线几何性质可知，AFC1和BGC1为有心扇形场，只是该扇形场在MNC微刚性区发生速度不连续变化。

（5）依据边界条件可以判断自由表面α和β滑移线方向上的合力指向外法线方向，左半部分塑性变形区AM，AC，AF为α线，平行于CFD的弧线为β滑移线，而右半部分塑性变形区BN，BC，BG为β线，平行于CGE的弧线为α滑移线。

（6）根据塑性变形秒流量相等原则，所以速端图闭合，如图3中所示，C1，C，M，N四个点极为接近，应力求解中刚性小三角形可以忽略。

2 应力求解与讨论

由于MNC为微刚性区，M和N点接近于C1点，可认为σyM=σyN=σyC1，基于汉基应力方程式，如果沿β线（弧线MD1），有

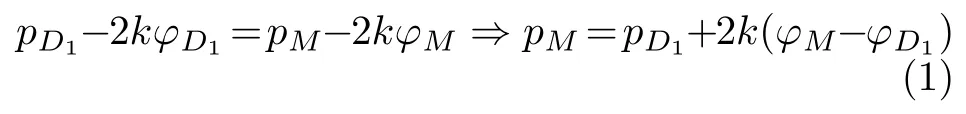
由于D1点为自由表面上的点，因此pD1=k，而根据β线时应遵守α线相同曲率方向或图示滑移线方向，可得

将式（2）中任一组角度代入式（1），均可得到

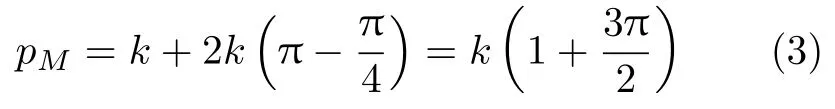
如果沿α线（弧线NE1），E1为自由表面上的点，因此pE1=k，然后据滑移线α的速度方向，确定角度，代入汉基应力方程式，可得

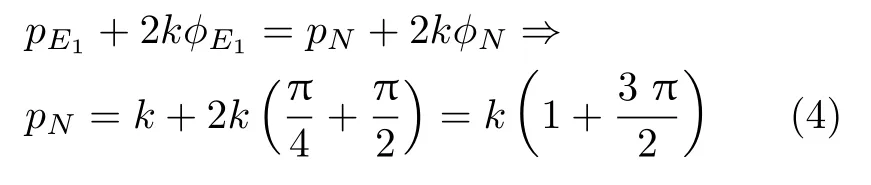
由式（4）可见，沿不同的滑移线得到的AB线上的静水压力相同，即N点处静水压力等于M点处静水压力值。

在得到M点处的静水压力后，按照点的应力张量与静水压力关系，可得到该点处应力张量分量分别为

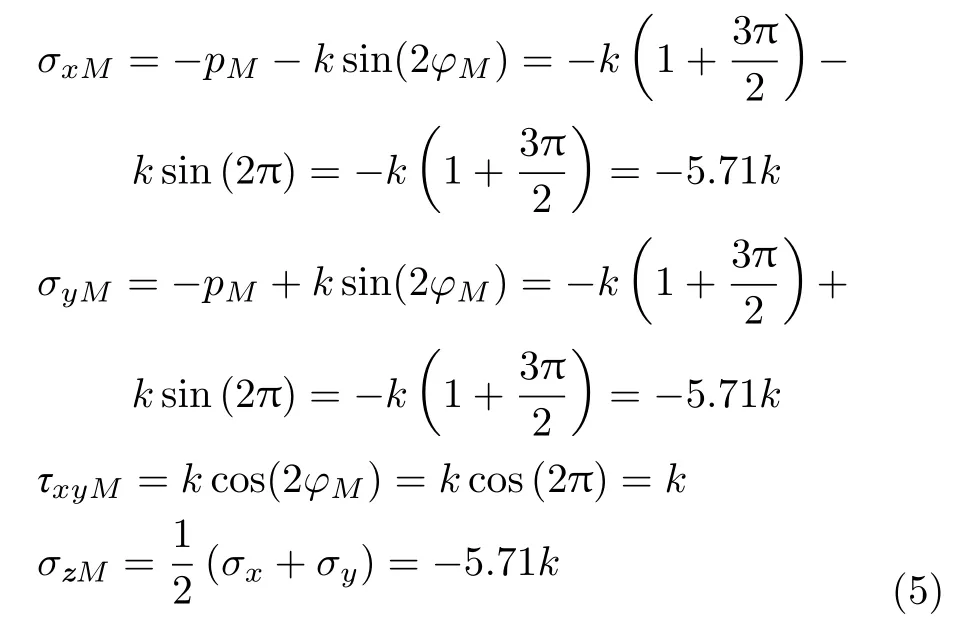
根据式（5）可以得到粗糙平冲头压入半无限体时试样与冲头接触面的平均单位压力为

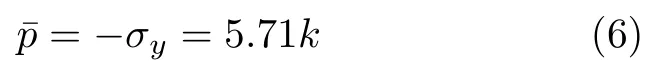
根据屈雷斯加屈服准则中屈服应力与剪切屈服强度关系，σs=2k，可得应力状态影响系数为

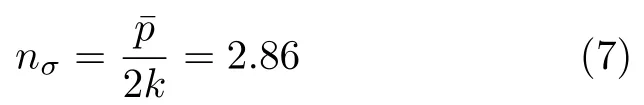
该滑移线场求解的单位压力5.71k明显大于Prandtl场的求解值5.14k[5]。通过与光滑平冲头压入半无限体结果对比[7]，可以判断出由于受到摩擦作用，接触面y方向单位接触压力和应力状态影响系数增加了11%，而x方向的应力增加更为明显，约为82%，受摩擦影响金属在x方向流动困难。计算结果相比Prandtl解更能准确反映外摩擦使塑性变形力和能耗增加的塑性变形理论，构建的滑移线场合理可靠。另外，由于Prandtl解与光滑平冲头求解结果相同，可认为5.14k是粗糙平冲头压入半无限体的平均单位压力下限解，而本文所得5.71k为上限解。

3 结论

根据滑移线性质和黏着接触摩擦条件的应力边值特征，构建了粗糙平冲头压入半无限体的非Prandtl滑移线场，得到了粗糙平冲头压入半无限体平均单位压力上限解为5.71k。与Prandtl滑移线场计算结果相比，接触面y方向单位接触压力和应力状态影响系数增加了11%，与光滑平冲头压缩半无限体计算结果相比，x方向的应力增加约82%，受摩擦影响金属在x方向流动困难，计算结果更能准确反映外摩擦使金属塑性变形力增加的塑性变形理论，构建的滑移线场合理可靠，有助于学生理解及滑移线理论的研究和实际应用。