混合长度理论教学中的拓展性讨论

贾 攀

(哈尔滨工业大学(深圳)理学院, 广东深圳518055)

流体流动有层流和湍流两种基本状态。在自然界和工程应用中层流较为少见，流动大多为湍流，故而对湍流的讨论也是不同层次流体力学教学中最核心的内容。通过对控制方程进行合理地简化，层流问题一般可求得解析解或者近似解；然而，对于湍流问题而言，由于控制方程固有的数学困难，无法解析求解，需要通过计算流体力学的方法数值求解。

湍流最显著的特点之一是流场的瞬时速度和压强在时间上表现出明显的脉动。1894年，英国曼彻斯特大学物理学教授雷诺提出将瞬时速度和压强分解为时均值和脉动值之和，即u=u¯+u′和p=+p′。进一步，将该分解代入不可压缩流动的连续方程和Navier-Stokes方程，即可得到描述平均流动的雷诺时均方程组如下

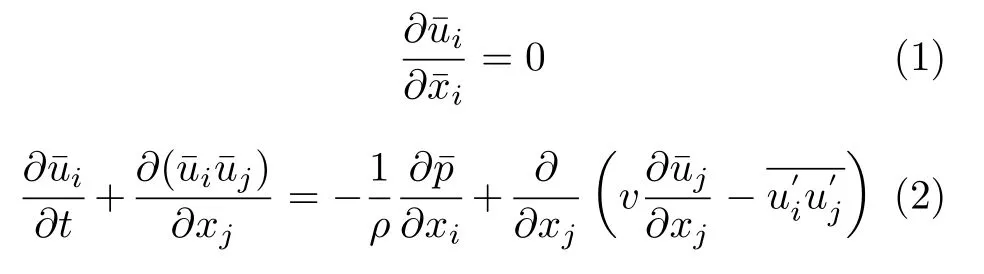
其中，v和ρ分别是流体的运动黏性系数和质量密度。相比于瞬时流动的Navier-Stokes方程，雷诺时均流动方程（2）中额外包括一个二阶脉动关联项，该项来源于对非线性对流项∂(uiuj)/∂xj的平均运算；为二阶对称张量，包含6个独立分量，具有应力量纲，通常称之为雷诺应力。上述方程组中包括4个分量方程，但是除了4个未知数u¯i和p¯ 之外，还有6个雷诺应力的分量未知；显然，未知数的个数大于方程的个数，该方程组不封闭。若要求解，则须将雷诺应力和时均流场关联起来，此即为求解湍流流动的封闭问题，相应的关联式称之为湍流模型。1877年，法国物理学家Boussinesq引入涡黏性系数的概念，发展了第一个湍流模型，即涡黏性模型[1]。在该模型的基础上，人们相继发展了混合长度理论[2]和关联于湍动能输运和耗散的K-ε模型[3]。后续，独立于涡黏性假设，人们又针对各向异性湍流发展了雷诺应力微分模型[4]。

在现有的模型中，混合长度理论的物理图像清晰明了，是物理学中比拟思想最直接的范例之一，对边界层流动、管道和槽道流动，以及各种自由剪切流动的模化十分有效，目前已广泛应用于大气科学[5]、海洋科学[6]以及恒星内部流动分析[7]。此外，该模型简洁的数学形式，允许进行一定程度的数学解析分析。因此，混合长度理论是国内外不同层次流体力学教材中介绍的重点内容[8-16]。然而，大多教材都是在简要提及混合长度理论的比拟思想之后即着重讲述混合长度的估计方法，对混合长度理论的优缺点，以及适用分析的流动则较少讨论，对该理论的发展和拓展性讨论更是少有阐述，因此，学生往往缺乏对该理论的透彻理解。这种情况下，学生在面对教材例题之外的问题时，比如近壁面流场中的黏性效应，壁面粗糙度效应等，往往十分困惑，无法准确判断是否可以使用混合长度理论；对混合长度理论的进一步发展和改进更是困难。

本文首先简要回顾混合长度理论的基本思想，然后以固体壁面剪切流动为对象，从近壁黏性和流向压强梯度效应、壁面粗糙度以及周期性波纹型壁面三个角度对混合长度理论的应用进行拓展性讨论。这将有助于教师帮助学生更加全面地理解混合长度理论，从而能够在分析实际流动问题时准确选用。

1 混合长度理论简述

1925年，德国科学家Prandtl将湍流流场中流体微团的脉动比拟于气体分子的热运动，提出了混合长度理论[2]。他假设流体微团在运动一段距离l之后才和它周围的流体微团发生动量交换，速度在运动的过程中则保持不变。在该假设下，流体微团运动的距离l可类比于气体分子运动的平均自由程，称之为“混合长度”。混合长度的估计方法是多数流体力学教材详细着墨的内容[8-9,12,15]，在此不再赘述，仅简要说明思路。如图1(a)所示，以平直壁面的剪切流动为例，z0处的时均速度为u¯(z0)， 假 设z0-l处的 流 体 微团沿z轴 正 方 向（脉动速度w′>0 ）运动距离l之后才和周围的流体混合，同时认为该流体微团混合前后的时均速度u¯ (z0-l) 和u¯ (z0) 之差 为z0处 的速度脉 动。由于l为小量，可通过泰勒级数展开、保留线性部分得到脉动速度的量级为-l(du¯/dy)|z0。类似地，可通过z0+l处的流体微团向下（w′<0 ）运动距离l之后和z0处的流体微团混合，得到z0处的速度脉动量级为l( du¯/dy)|z0。由于z0处的流体微团可随机地来自z0-l或z0+l处，因此在一段时间内从上方和下方抵达的概率是相等的，于是z0处的速度脉动应该与上述得到的两个脉动速度均值的量级相同，即进一步假设z方向的速度脉动w′与u′量级相同，同时考虑到通常u′w′<0 ，于是有，最终可得

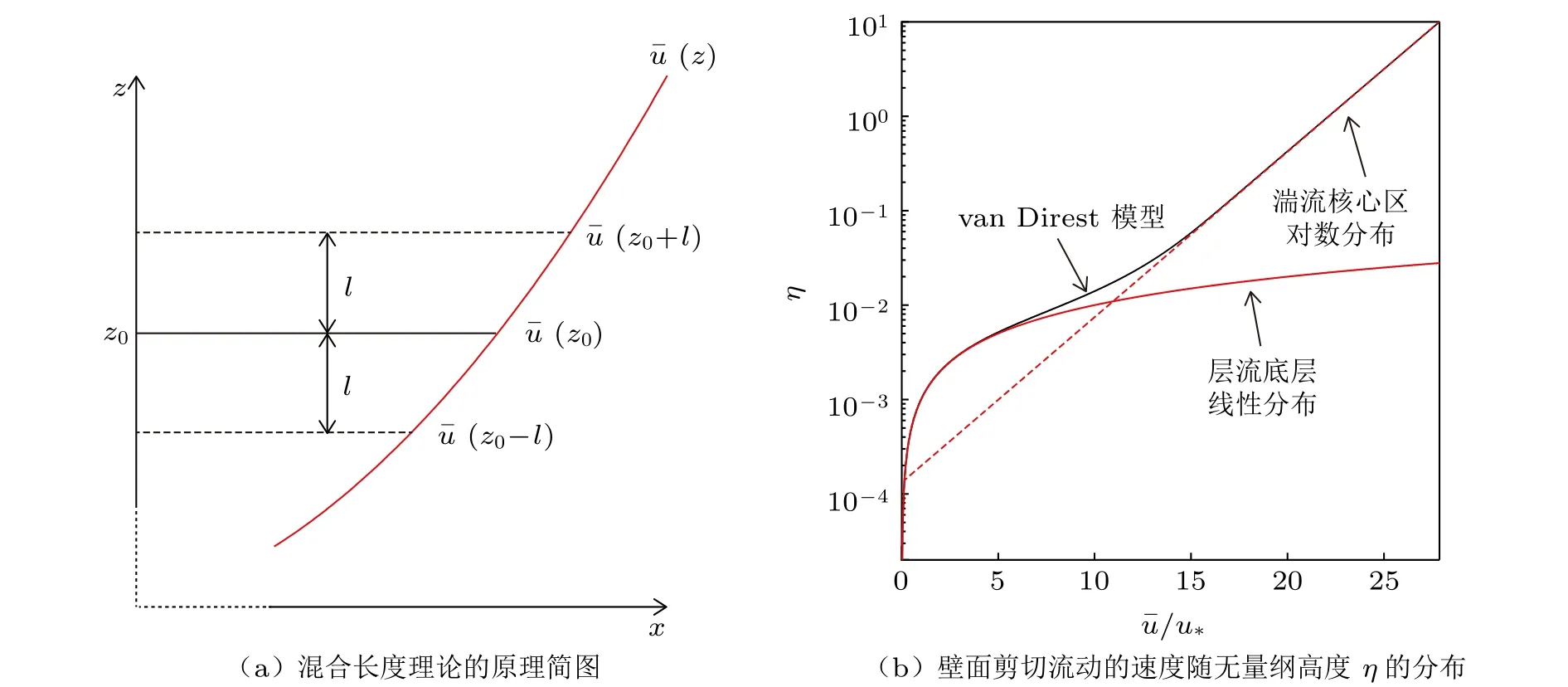
图1 平直壁面的剪切流动

其中，尺度化符号转化为等号的过程中出现的比例效应已经包含在混合长度l中。因此，涡黏性系数可估计为vt=l2|d/dy|。由上文讨论可知，混合长度理论中涡黏性系数的估计涉及到一个混合长度和一个混合频率，它们分别表征了湍流场中特征涡的长度尺度和时间尺度[14]。一般情√况下，混合频率由流场应变率的模给定其中=∂ui/∂xj+∂uj/∂xi。于是，湍流流场中分子扩散引起的黏性切应力和湍流脉动导致的雷诺切应力之和可表示为

在回顾了混合长度理论的基本思想之后，我们从三个角度探讨流体力学教学中针对混合长度理论的拓展性讨论。

2 拓展性讨论之一：平壁表面剪切流场的完全描述

对于平壁附近剪切流动，若已知壁面处的切应力为τ0=ρu2∗，其中u∗为摩擦速度，理论上即可求解流场的平均速度廓线。当流动方向的压强梯度为零时，对时均流动的控制方程沿垂直于平板方向积分可得

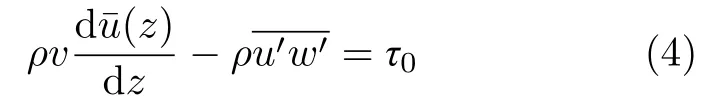
在近邻壁面处存在一个黏性底层，该层内黏性起主导作用，雷诺应力可忽略，故而时均速度呈线性分布

黏性底层之外，惯性效应占优，黏性可以忽略，流动处于完全湍流状态，称之为湍流核心区。若通过混合长度理论来模化雷诺应力，即可得到湍流核心区的时均速度廓线。Prandtl认为混合长度取值不受流体黏性的影响；同时，由于流场中一点到壁面的距离z是流动中唯一的长度尺度，因此可假设l=κz；该假设也意味着在=τ0成立的长度尺度范围内，流场中一点处的动量输运，不会受到长度尺度比该点到壁面距离z大的涡的影响，也不会受到壁面附近小涡的影响。结合流动控制方程，可得湍流核心区的速度廓线呈对数分布

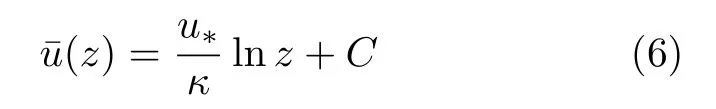
其中C为待定的积分常数，κ≈0.4 为von Karman常数，对于光滑壁面C≈5.0[8,14]。

以上通过混合长度理论得到湍流核心区对数律平均速度廓线的讨论通常作为典型的应用范例，可见于流体力学教材[8-9,12,15]。其实，在黏性底层和湍流核心区之间还存在一个黏性应力和雷诺应力都比较重要的过渡区（也称缓冲区）。显然，在黏性底层和过渡区内，速度分布都不遵循方程（6）所示的“对数律”，故而混合长度理论不能直接使用。如何实现固壁湍动剪切流场的完全描述，可作为混合长度理论教学的拓展性讨论之一。

若将方程（3）应用于黏性底层，我们可得O(y3)，l～O(y3) 。因此，湍流核心区混合长度的估计形式l=κz并不适用，需要进行衰减处理。1956年，van Direst通过引入一个指数形式的阻尼因子来改进混合长度，实现了固体壁面湍动剪切流场的完全描述[17]。改进之后的混合长度估计形式为

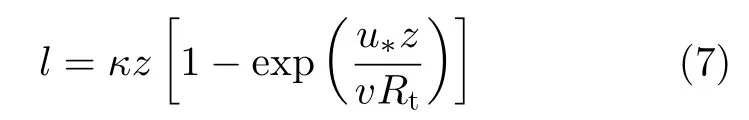
其中，Rt为过渡雷诺数。对于流动方向压强梯度为零的于平壁剪切流动来说，Rt0≈26 。将方程（3）代入方程（4）求解即可得

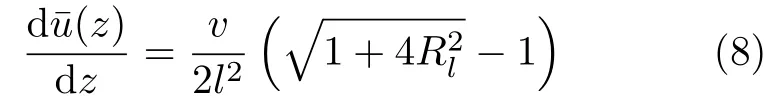
其中Rl=u∗l/v。进一步，将方程（7）代入并积分即可得到固壁面附近完整的平均速度廓线，如图1(b)所示无量纲之后的速度廓线。在壁面附近的黏性底层内（z→0 ），可得∝z的线性变化关系；远离壁面处，方程（7）中的指数项衰减趋近于零，从而可再现湍流核心区内的对数律速度分布（方程（6））。虽然van Direst修正模型是经验性的，但是能很好地同时应用于黏性底层和湍流核心区，实现了两者之间的光滑过渡（图1(b)），该修正适用于多种壁面流动模型，尤其在大涡模拟中广泛使用[18]。

除了近壁面处黏性底层的影响之外，流动方向的压强梯度也会对混合长度的估计有影响（本节上文讨论中，假设压强梯度为零，见方程（4））。1967年，Smith 等[19]在 van Direst模型（方程（5））的基础上，对Rt进行了修正，来考虑压强梯度的效应

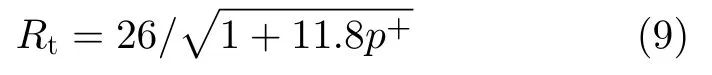
其中p+=[v/(ρu3∗)](dp/dx) 。为了使不同层间速度廓线之间光滑过渡，Granville[20]在1989年又对Rt中的相关系数作了进一步修正。下文中，我们还将对波纹型壁面导致的压强梯度效应进行讨论（第4节）。

3 拓展性讨论之二：固体壁面的粗糙度的影响

上文讨论了主要针对光滑壁面的情况。然而在实际流动中，壁面总是粗糙的；并且粗糙度等级（通过平均高度表征）对壁面切应力和流场时均速度廓线会有显著影响。壁面剪切流动中，黏性底层厚度的量级为δv～v/u∗；若壁面粗糙度的平均高度d<δv，则壁面的粗糙结构完全淹没在黏性底层中，湍流区不同尺度的涡感受不到壁面的粗糙结构，这种情况称之为水力光滑；反之，若d>δv，那么湍流区的涡会直接和表面的粗糙结构发生摩擦作用，造成可观的能量耗散，这种情况称之为水力粗糙。水力光滑和水力粗糙的基本概念多数教材会有简要地讨论，比如文献[8-9,12, 15]；但是，壁面粗糙度等级如何影响混合长度的估计，以及如何定量地分析粗糙度等级对流场速度廓线的影响，则鲜有提及，可作为混合长度理论教学的拓展性讨论之二。

为了考虑壁面粗糙度对混合长度的影响，Claudin等[21]在van Direst的基础上给出了估计混合长度，即[21]

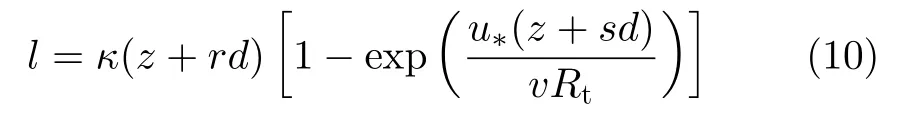
其中，r=1/30 和s=1/3 为无量纲参数，该取值通过测量具有不同粗糙度等级的固壁表面剪切流动的速度廓线标定得到[22]。实际上，rd对应于流体动力学粗糙度，可通过将湍流核心区的对数速度廓线（方程（4））外推到速度为零时对应的壁面距离给定，如图1(b)所示；显然，rd直接关联于壁面和流体界面上的摩擦力和动量输运。sd关联于黏性底层的厚度，随着壁面粗糙度等级的增加，黏性底层的厚度被抑制。以粗糙度的平均高度为特征长度，我们定义雷诺数Rd=u∗d/v，用以表征粗糙度的平均等级和黏性底层厚度的相对大小，判断壁面流动的光滑和粗糙特性。图2中给出了不同Rd下，壁面剪切流动的时均速度廓线和流体动力学粗糙度。当Rd较小时，壁面是水力光滑的，黏性底层相对较大，靠近壁面处速度线性分布（图2(a)中橙色曲线）；此时，流体动力学粗糙度基本不随Rd变化，由黏性底层的厚度δv～v/u∗决定。当Rd较大时，黏性底层隐藏在壁面粗糙结构之内，过渡区也很薄可以忽略，整个流场几乎全部处于湍流状态，混合长度直接正比于到壁面的距离，速度廓线呈对数变化（图2(a)中黑色和蓝色曲线），相应地，流体动力学粗糙度，由壁面粗糙度高度决定，随Rd的增大而增大（图2(b)）。

4 拓展性讨论之三：周期性波纹型壁面剪切流动的描述

前文有关混合长度的估计针对的都是平直壁面上的剪切流动。实际上，该理论也可推广到非平直壁面剪切流动的情况，这一点可作为混合长度理论教学的拓展性讨论之三。

为了不失一般性，我们考虑轮廓按三角函数形式变化的波纹型壁面（图3(a)）。在只关注实部的情况下，壁面轮廓的数学描述可表示为Z(x)=ζexp(ikx)，其中ζ为壁面幅值，k=2π/λ为波数，λ为波长。其他形式的壁面轮廓都可通过傅里叶级数叠加的思想得到。对于波纹型壁面，由于伯努利效应，从波峰到波谷的流动中流速降低，压强上升；相应地，从波谷到波峰的流动中，流速上升，压强下降；因此流动方向会存在一个周期性变化的压强梯度，需要指出：该梯度并不与壁面轮廓保持同相位变化[23]。由于该压强梯度的存在，Rt不能取常数，van Direst模型不可直接使用；此外，由于是非平直壁面，前文第2节关于压强梯度的修正亦不适用。针对这种情况，Hanratty[24]于1981年研究指出Rt的取值依赖于一个在空间相位上滞后于压强梯度的无量纲数H，由以下弛豫方程描述

其中τxx为应力分量，a为H的空间相位滞后的无量纲数值系数，b=(1/R0t)(dRt/dH) 表征由于压强梯度导致的Rt的相对变化。通过实验测得的波纹壁面切应力的变化特性，标定可得a=2000和b=35[25]。

对于波纹壁面来说，时均流动不再是平行流动，即使在给定混合长度的情况下，由于非线性对流项的存在，流动的控制方程组也无法解析求解。对于kζ较小的情况，通常可通过线性稳定性分析的思想求解流场：以平直壁面的流动作为基态，然后引入傅里叶模态对基态流场进行扰动，扰动后流场参数f(x,z) 的一般形式可表示为

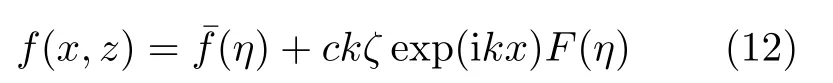
其中η=k(z-Z) 为z方向的无量纲坐标，为基态流场信息；右边第二项为扰动项，其中比例系数c为有量纲量，用以匹配各物理量的单位，F(η)为无量纲的模态函数，用以描述流场物理量在z方向的变化。通过这种思路线性化时均流动的Navier-Stokes方程，并结合van Driest和Hanratty对混合长度估计方法的修正，求解可得波纹壁面剪切流场的全息信息。详细求解过程，读者可参考文献[26]。

在这类流动中，壁面切应力一般是最为关注的物理量，按照方程（12），可表示为

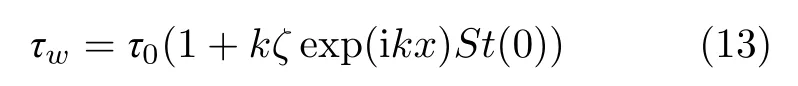
因此，只要确定切应力对应的模态函数St在η=0处的值，即可确定壁面上的切应力分布。分析表明St(0) 为复数，这表明壁面切应力相对于壁面轮廓除了数值上的差别之外，还存在一个相位差。取St(0)=A+iB，容易理解：A和B的取值依赖于壁面附近的流动状态（由壁面雷诺数Rλ=u∗/(kv) 表征）。图3(b)和图3(c)所示为A和B随Rλ的变化规律。显然，Rλ在 10-4～10-3范围内，相位差φ=arctan(B/A)>0 均成立；因此，壁面切应力相对于轮廓存在一个相位提前；也就是说，最大壁面切应力出现在波峰之前，并且在Rλ≈10-3附近出现了剧烈的变化，这些结果已经在实验中证实，进一步的讨论可参考文献[25]。

在这部分的拓展性讨论中，我们探讨了混合长度理论在周期性波纹型壁面剪切流动模化中的应用。波纹型壁面在自然界很常见，比如沙漠和河床表面，以及行星环境下的波纹构型，它们的形成和演化都依赖于壁面上的剪切流动引起质量和能量输运，已有学者借助波纹壁面的混合长度理论对这些构型进行了深入地讨论[25-26]，在教学中可通过这些有趣的应用来激发学生学习湍流理论的好奇心和兴趣。

5 结语

本文以固体壁面的剪切流动为例，从近壁黏性和流向压强梯度效应，壁面粗糙度以及周期性波纹型壁面的剪切流动三个角度对混合长度理论的拓展性教学给出了方案。前两种讨论是混合长度理论直接相关的扩展，可作为本科层次的教学拓展讨论；有关基于混合长度理论对波纹型壁面剪切流动分析，需要对流动稳定性分析的思想有所了解，可作为研究生层次的拓展讨论内容。经过这样的拓展性讨论教学之后，将加深学生对混合长度理论的理解，帮助学生厘清混合长度理论的适用范围，具备准确地应用于相关流动分析的能力。在拓展性教学的基础上，笔者还认为应该探讨混合长度理论的一些固有缺陷，比如，不同于气体分子之间的碰撞，流体微团的互相作用是连续的，两者直接比拟比较牵强等。如此，学生可以对混合长度理论有一个更加全面客观的理解。