二维圆柱对旋转单极子点源的声散射

薛丝丹，钱振昊，何嘉华，刘秋洪

（1.西北工业大学翼型叶栅空气动力学重点实验室，西安 710072；2.中国空气动力研究与发展中心气动噪声控制重点实验室，四川绵阳 621000）

在过去几十年中，旋转叶片产生的气动噪声问题一直是航空声学的研究热点，目前已经在理论分析和数值计算方面取得一些重要的成果。早期理论研究，包括Ffowcs Williams 等[1]、Lowson[2]以及Morfey 等[3]的工作，都倾向于将旋转叶片噪声源简化为理想的旋转点源，以点源模型预测旋转叶片噪声。另一方面，越来越多的研究者从计算流体动力学（CFD）和声比拟理论出发，将旋转叶片噪声源视为一系列旋转运动点源分布，采用时域[4-5]或频域[6-7]数值方法预测噪声。

研究旋转点源的声场精确解有助于发展高精度的噪声数值预测方法。吴九汇等[8]最早应用球谐级数展开方法建立了旋转点声源在自由空间中的理论解析解。Poletti[9-10]提出了旋转二维和三维单极子点源声辐射精确时域球谐解。Carley[11]提出了一种用级数展开法预测旋转单极子点源辐射噪声的理论模型。Mao等[12]利用球坐标系和柱坐标系级数展开法，推导了旋转单极子和偶极子辐射声场的精确解。进一步地，Mao 等[13]推导了旋转四极子点源声辐射精确解。这些理论模型都假设点源在自由场中旋转。

实际应用中，旋转点源辐射的声波会因周围声学边界条件的存在而发生散射效应，比如机翼和机身等结构对螺旋桨噪声的散射，使得实际声场与自由空间辐射声场存在明显差异。在已发表的学术文献中，使用理论解析方法对结构的声散射进行了有限的关注。Glegg[14]将螺旋桨声源建模为旋转偶极子点声源、中心体简化为无限长的刚性圆柱体，得到一个预测螺旋桨远场声压的公式，其中包含了轮毂的散射。Kingan 等[15]扩展了Glegg 的工作以评估中心体散射对开式转子噪声的影响。Hanson等[16]提出了一种计算飞行器机身散射开式转子噪声的方法，机身被简化为无限长声学刚性圆柱体。McAlpine等[17]应用Hanson 等的分析进一步评估机身散射对旋转单极子或偶极子点源以及开式转子噪声的影响。Kingan等[18]也进行了类似的研究。毛义军等[19]对旋转声源辐射噪声和边界散射噪声的预测方法进行了综述。

理论模型对实际物理问题进行了太多简化，需要发展可靠的数值方法以提高旋转点源的声场预测精度。本文基于点源模型，利用边界积分方法研究二维声学边界对旋转点源的声散射效应。为验证数值方法的可靠性，对二维圆柱的声散射进行了理论建模分析。

1 声散射计算的边界积分方法

观察点与源点的位置和时间分别用x和y以及t和τ表示。如图1所示，刚性固体边界S附近有一简谐振动角频率为ωs的单极子点源q（y,τ），以角频率ωr绕o点逆时针旋转，其初始相位和振幅分别为0和1，即点源可表示为：

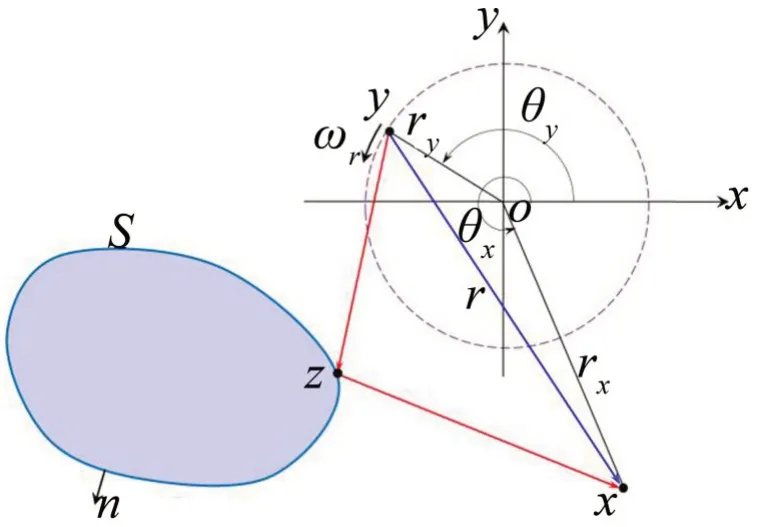
图1 旋转点源声传播示意图

那么，时域下的声学控制方程为：

式中：c0为声传播速度。在刚性固体边界上，声场应满足声学硬边界条件：

方程式（2）的基本解为自由空间格林函数G0（x,y,t-τ ），满足方程（4）：

利用方程式（2）～方程式（4）可得到：

根据Fourier变换定义：

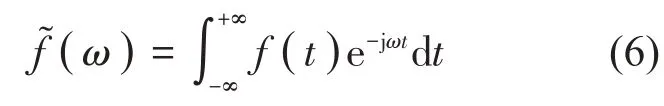
频域自由空间格林函数为：

因此方程式（5）可在频域下写成：

式中右端两项分别为入射声和散射声。

以点源旋转中心为坐标原点建立极坐标系，观察点x和源点y的位置分别为（rx,θx）和（ry,θy），假设点源的初始位置为θ0，则有：

假设声传播介质静止、均匀，对二维声传播问题，频域自由空间格林函数为：

其级数展开形式为：

其中：Jm（ · ）表示m阶Bessel 函数，Hm（2）（ · ）表示m阶第二类Hankel函数，r＜=min（rx,ry），r＞=max（rx,ry），k=ω c0为声学波数。将式（1）、式（10）和式（12）代入方程式（9）得到：

利用Dirac函数性质：

得到声入射的表达式为：

将散射边界离散为N个网格单元，采用等参边界元方法求解方程（8）以获得散射边界上的声场。当观察点置于散射边界时，积分方程式（8）可离散为一系列线性方程组：

写成矩阵形式为：

其中：

2 圆柱声散射理论解析解

二维圆柱几何形状简单，易获取散射场的理论解析表达式。将观察点的声学压力场分解为自由入射声场和圆柱散射声场两部分，前者可由式（15）决定，还需得到后者的解析表达。类似于式（9），假设圆柱声散射的表达为：

2.1 点源与圆柱同轴旋转

点源q（y,τ）绕圆柱同轴旋转如图2 所示，假设散射格林函数可表示为：

图2 点源绕圆柱同轴旋转示意图

当观察点位于圆柱表面时，将式（12）和式（20）代入声学边界条件（3），可解得：

式中：

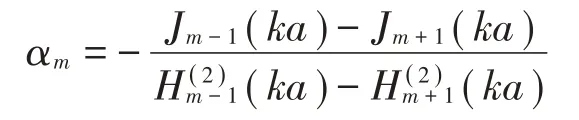
即有：

将式（1）、式（10）和式（22）代入式（19），利用式（14）得到：

2.2 点源与圆柱异轴旋转

如图3 所示，二维圆柱附近有一旋转单极子点源q（y,τ），其旋转中心与圆柱中心的距离为d，以点源旋转中心点为坐标原点建立极坐标系，对应的观察点x和源点y的位置分别为（rx,θx）和（ry,θy）；同时以圆柱中心点为原点建立另一极坐标系，对应观察点x位置为当观察点位于圆柱表面时，显然有rx＞ry和＜d。根据Graf加法定理，

图3 点源与圆柱异轴旋转示意图

可将自由空间格林函数改写为：

其中：ϕ=π+α。

进一步令：

利用式（1）和式（10），分别将式（25）代入式（9）、式（26）代入式（19），根据边界条件式（3）和关系式（14），可解得：

式中：

从而散射格林函数可写为：

将式（28）代入式（19），积分可得：

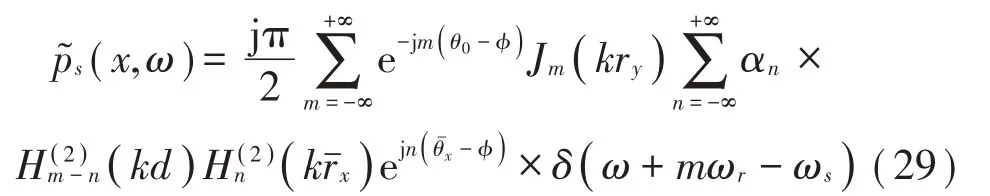
旋转单极子源的解对m具有无限项，在实际应用过程中应以截断方式采用有限项计算，截断项数M与观察点感兴趣的声波频率ω有关，当ω小于源谐振频率ωs时,截断项数应保证ω＜Mωr-ωs，也就是；当ω大于源谐振频率ωs时，应满足。除此之外，根据Bessel 函数的指数衰减性质，M不小于，[ · ]表示向上取整数。基于上述的分析，截断数M应该满足：

3 二维圆柱算例验证

采用等参边界元方法计算单极子点源与圆柱同轴和异轴旋转的声辐射特性，将结果与理论解析解对比，验证数值方法的正确性。取圆柱半径a=1.0 m，单极子点源的初始位置θ0=0°，其谐振频率和旋转频率分别为

3.1 点源与圆柱同轴旋转算例验证

如图2 所示，取ry=1.5 m。采用边界元方法进行声传播计算时，需要足够的网格数量以保证数值结果与网格无关。在圆柱表面均匀分布180个网格单元，对500 Hz 以下的声波，一个波长范围内不少于20个网格单元，可以满足网格无关性要求。数值积分采用四点高斯积分方法，线性方程组的求解采用全选主元高斯消去法。

图4为观察点（rx=10 m,θx=0°）的声压幅值谱，边界元数值解与理论解吻合一致。与固定点源产生的单频声场不同，旋转点源因存在多普勒效应，产生的噪声分布在一系列离散频率上，离散频率满足关系式ω=ωs-mωr，其中m为谐波阶次；最高峰值频率为f=160 Hz，对应的谐波阶次为m=4。在低频（小于100 Hz）和高频（大于400 Hz）处，声压几乎为0。

图4 点源绕圆柱同轴旋转时观察点声压幅值谱（rx =10 m,θx =0°）

图5为圆柱表面上160 Hz声压幅值指向性分布的边界元数值结果与理论解析结果的对比图。对不同的网格单元，数值解与理论解的一致性非常好。对相同极半径的观察点，声压的幅值是相同的，呈现出典型的单极子声场特性。

图5 点源绕圆柱同轴旋转圆柱表面160 Hz声场指向性分布

图6 为边界元方法计算得到的140 Hz、200 Hz和260 Hz总声压实部的空间分布云图，对应的谐波阶次分别为m=6、m=0 和m=-6。从图中可以看到，m=0的声波呈同心圆状向外辐射；而m≠0的声波则以螺旋状向外辐射，螺旋瓣的数量与 |m|相同，且m＞0 时螺旋瓣的方向与点源旋转方向相反，而m＜0 时则相同。

图6 点源绕圆柱同轴旋转时声场分布云图

3.2 点源与圆柱异轴旋转算例验证

对如图3 所示的点源与圆柱异轴旋转算例，选取ry=0.5 m、0°和d=2.0 m。边界元方法的数值计算采用与同轴旋转算例一致的网格，以及相同的数值积分和线性方程组求解方法。

图7 为观察点（=10 m，=0°）的声压幅值谱，边界元数值解与理论解再次吻合一致。异轴旋转点源产生的噪声分布在一系列离散频率上，这与同轴旋转的频谱特性相似，最高峰值频率为f=210 Hz，对应的谐波阶次为m=-1。

图7 点源绕圆柱异轴旋转时观察点声压幅值谱（=10 m, =0°）

在=10 m 的圆周上取不同的观察点，将数值计算的声压幅值与理论解析结果进行对比。图8为210 Hz声场的声压幅值指向性分布，对不同的观察点，数值解与理论解是一致的。由于圆柱对声波的散射作用，声场的空间分布趋于复杂化，不像同轴旋转那样具有显著的规律特征。

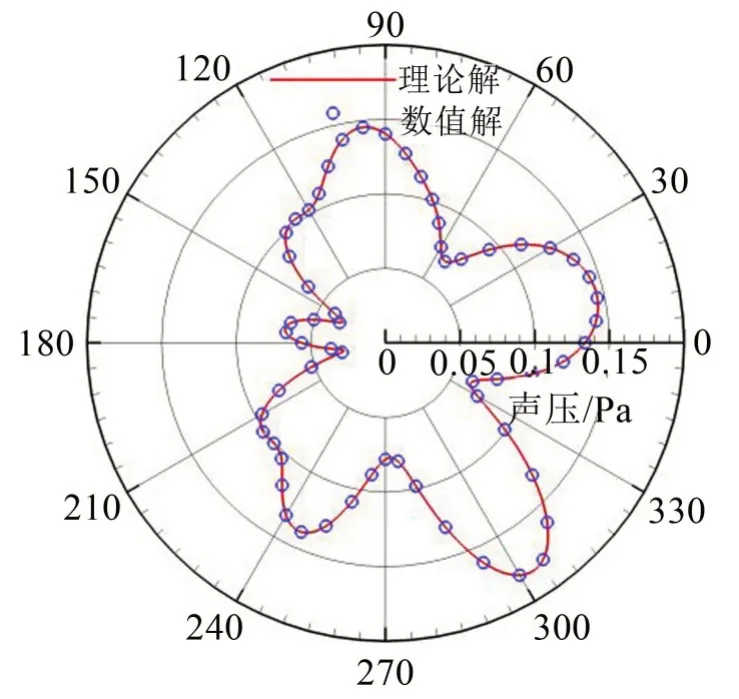
图8 点源绕圆柱同轴旋转时声场指向性图（ =10 m, f =210 Hz）

图9为边界元方法计算得到的210 Hz声场的自由入射声压、圆柱散射声压和总声压实部的空间分布云图。入射声波以明显的螺旋状向外辐射，这是由点源的旋转运动特性决定的。与同轴旋转算例不同的是，圆柱对异轴旋转点源入射声波的散射不再具有单极子的螺旋状特性，而呈现显著的偶极子特征，使得总声场在多个方向存在强传播。

图9 点源绕圆柱异轴旋转时210 Hz声场分布云图

4 结语

对任意形状的刚性散射边界，利用自由空间格林函数的级数展开式求解线性声学波动方程，建立了旋转单极子点源声辐射的频域边界元数值计算方法。同时，根据贝塞尔函数的加法定理，推导了点源与二维刚性圆柱同轴、异轴旋转状态下的声场理论解析表达式。

对点源与圆柱同轴、异轴旋转两个算例，边界元方法的数值解均与理论解析解吻合一致。点源向外辐射声波的频率由点源谐振频率、旋转频率和谐波阶次共同决定。对同轴旋转算例，谐波阶次为0 的声波以同心圆状向外辐射，不为0 的声波则以螺旋状向外辐射，螺旋瓣的数量与谐波阶次的绝对值相同。对异轴旋转算例，圆柱的声散射呈现显著的偶极子特征，声场的指向性复杂，不像同轴旋转算例具有显著的螺旋辐射特征。

在后续的研究中，将进一步考虑旋转偶极子、四极子点源的声辐射特性和运动介质的影响，以及将二维声传播的研究结果推广到三维声学问题的研究。