非刚性管中换能器灵敏度的测量方法研究
2022-10-20于龙晶王月兵唐佳玄郑慧峰
于龙晶, 王月兵, 唐佳玄, 郑慧峰
(中国计量大学 计量测试工程学院,浙江 杭州 310018)
1 引 言
随着水声探测领域的不断扩展,声信号监测设备在海洋环境的探测与资源信息的获取中发挥着越来越重要的作用。具有舰载声呐一些无法比拟的优点,线列阵已在许多国家的海军中应用[1,2]。根据线列阵工作时是否移动阵列位置,可将其分为拖曳式线列阵和固定式线列阵两种类型。和其他测量设备相同,在使用过程中为了保证信息获取的准确性,需要定期对线列阵阵元的灵敏度进行校准[3]。对于拖曳式线列阵的校准比较方便,可以直接对拖曳阵利用常规的各种换能器灵敏度校准方法进行校准[4,5];但海底固定式线列阵在应用时铺设于海底,周围有着大量混合海水的泥沙,结合其工作环境及较低的工作频率[6],此时提出适用于此类非刚性边界的低频换能器校准方法显得尤为重要。
目前常用的低频校准方法[7]主要有耦合腔校准、混响场校准[8]和管中测量等。管中测量方法又包括了振动液柱法、管中比较法(驻波管、行波管)以及行波管互易法[9]。早在1980年何祚镛就对耦合腔中刚性边界的声压的传播与互易常数的补偿做了理论推导与仿真分析[10]。2012年,研究水下混响测量技术的尚大晶将非消声水池壁面近似为纯实阻抗边界,得到了非刚性边界传播相较于刚性边界,简正波幅值变化但数量与波数几乎不受影响的结论[11]。以上研究均有很大的指导意义,但对于非刚性边界测量条件的较大型的换能器阵列校准的情况,刚性边界的耦合腔校准与混响场方法已经不能满足校准需求。在1966年Beatty L G对行波管中的刚性壁边界传播的互易常数进行了推导[12],之后薛耀泉等人利用行波管技术[13]在较大尺寸的刚性管中完成了20 Hz~4 kHz频率范围的换能器灵敏度校准。同样的,以上阐述的行波管测量的边界也为完全刚性,其中的互易常数无法直接应用,需要对非刚性边界的管中声压传播与互易常数进行重新推导。
在水声计量中,互易校准法是最常见最典型的一级校准法[14],使用时各个换能器的发送响应与接收灵敏度可以为未知,更适用于使用标准换能器不便的情况。因此本文将管中互易法作为基础,基于管中声场的公式推导出管中互易常数及其修正值,并对其进行理论仿真研究,得到特定情况下的随频率变化的互易常数值与修正值。利用比较法与自由场互易法[15]测量结果作为参照,在管中进行互易法的实验测量得到互易换能器的灵敏度曲线以及修正后的灵敏度曲线。结果显示,修正后的灵敏度曲线更接近自由场测得的灵敏度值,灵敏度曲线的变化在有效范围内,且与自由场互易法测得值误差较小,表明互易常数的修正是更准确且必要的。
2 管中互易常数的理论推导
针对管中测量环境下进行互易常数的理论推导,利用推导出的互易常数代入灵敏度计算公式,可以得到相应的灵敏度值。根据互易常数的定义可以知道,声压条件对于互易常数的计算有着至关重要的影响,因此对于管中声压的计算作为推导公式的第一步。
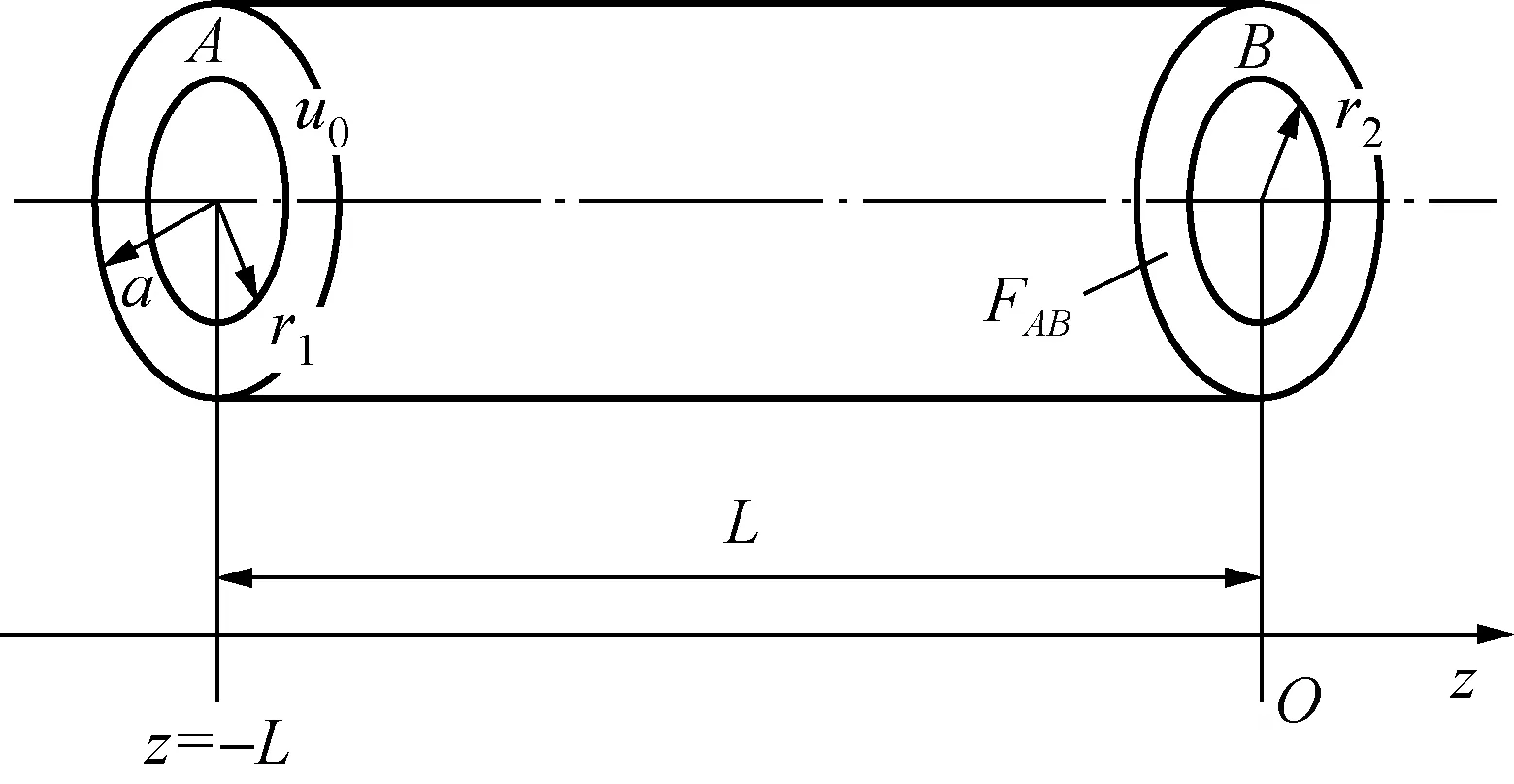
图1 管示意图及参数Fig.1 Tube schematic and parameters
如图1所示为长为L,半径为a的圆管,其中在管面A和B的位置分别有两只半径为r1和r2的换能器,发射换能器的发射面振速为u0。通过求解半径为a的刚性圆柱形管声波方程可以得到柱坐标下表示的管中声压公式[16]:
(1)
式中:J0是0阶柱贝塞尔函数;krm和kzm分别为径向和轴向的波数分量。刚性壁管中声压公式相乘于非刚性壁的损失函数[14]就可以得到非刚性管中的声压公式,损失函数表达式如下:
(2)
式中:ε为管壁声导纳率比的实数部分,表达式如下,其中ρ为管壁的材料密度,c为传播声速,Zs为壁面的声阻抗率。
(3)
由声压与质点振速的关系可以得到非刚性管中径向质点振速和轴向质点振速的公式:
(4)

① 管壁设为阻抗壁
(5)
② 终端边界
(6)
③ 阵元作活塞式振动
(7)
在这里,如图1所示,坐标设置起始点为-L,终点坐标为0,us表示边界的阻抗参数,具体的阻抗相关系数由后续推导为准。
由条件③和贝塞尔函数的正交性可以解出声压中的重要系数Am,此时采点间隔由m变为n,因此An表示为:
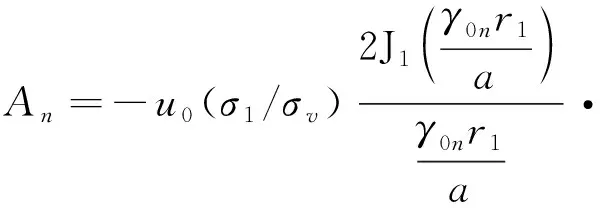
(8)
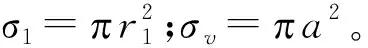
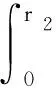
(9)
式中:γ0n为一阶柱贝塞尔函数的第n个解。因此根据互易常数的定义可以得出管中互易常数的计算公式:
(10)
式中:QF表示发射源强度;FAB表示发射换能器作用到接收面的力。求和公式中相乘的各项如下
(11)
其中:构造函数Λ1(x)=J1(x)/x。实际上存在ka<γ01,因此除了“γ00=0”一项,其他项皆有γ0n/ka<1,因此互易常数的误差项用dB值表示可以写为:
(12)
(13)
综合以上公式可知近似后的互易参量有一定的误差,因此本文将误差项ΔN补偿,补偿后的互易常数值也可以表示为
Jh=Jh0+ΔN
(14)
将行波管中的互易常数替换成补偿后的管中互易常数Jh,就可以得到补偿后的非刚性管中换能器测量灵敏度值。
(15)
式中:UFH、UHJ、UFJ为激励电压;IH为响应电流。
3 仿真分析
管长为L(实验中为1.3 m),换能器接收截面直径为30 mm,管中截面直径为100 mm。使用MATLAB基于推导出的互易常数理论式(10)进行仿真计算,将上述参数代入公式,可以得到未补偿时的非刚性管中互易常数值Jh0随频率的变化如图2。可以看到,理论情况下,在0~4 kHz的频率范围内,随着频率的增加,互易常数有上升趋势,0.5 kHz时值接近 -170 dB,4 kHz时互易常数值增加到-150左右。
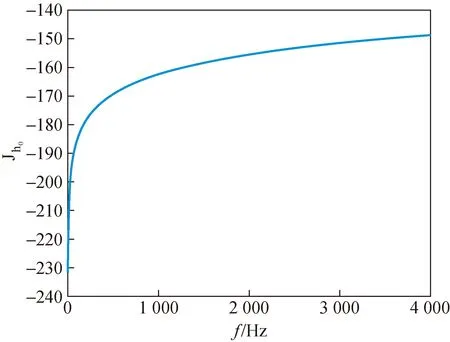
图2 互易常数随频率变化曲线Fig.2 Reciprocal constant versus frequency curve
根据理论推导中的式(12)得到的互易常数的补偿项,进行公式的理论计算,可以得到互易常数修正量随频率的变化如图3所示。
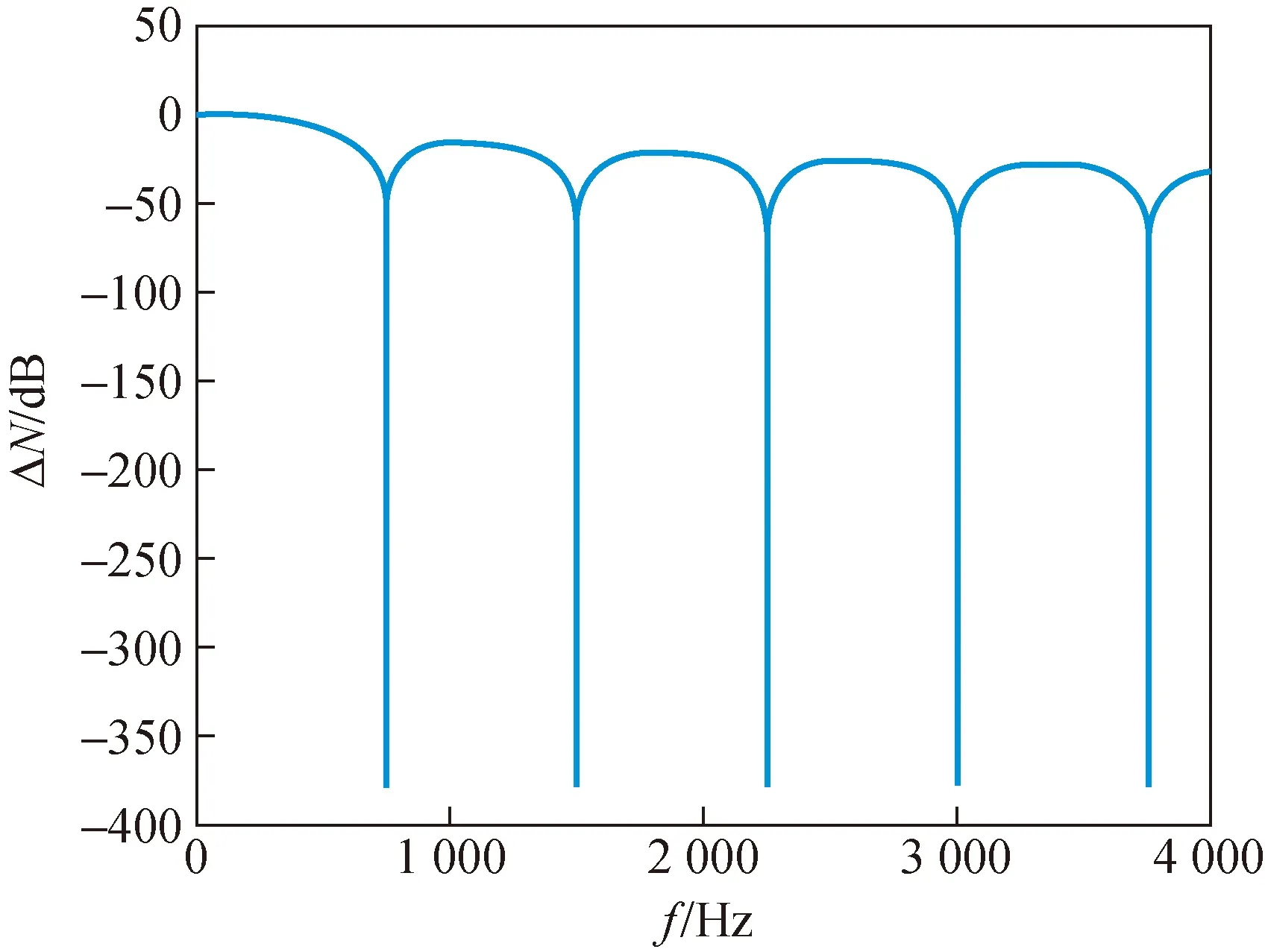
图3 互易常数修正量随频率变化曲线Fig.3 Reciprocal constant correction curve with frequency
可以看到该补偿函数在0.75 kHz、1.5 kHz等频率点处有明显骤降的奇点,可以反映出管中的声压传播特性。后续的实验为有效避开因贝塞尔公式涉及的补偿值在某频率点骤降引起的误差,可以根据实验设计的频率范围0.5 kHz~4 kHz和采样间隔为0.1 kHz重新采样,得到只有两个奇点的修正量曲线如图4。
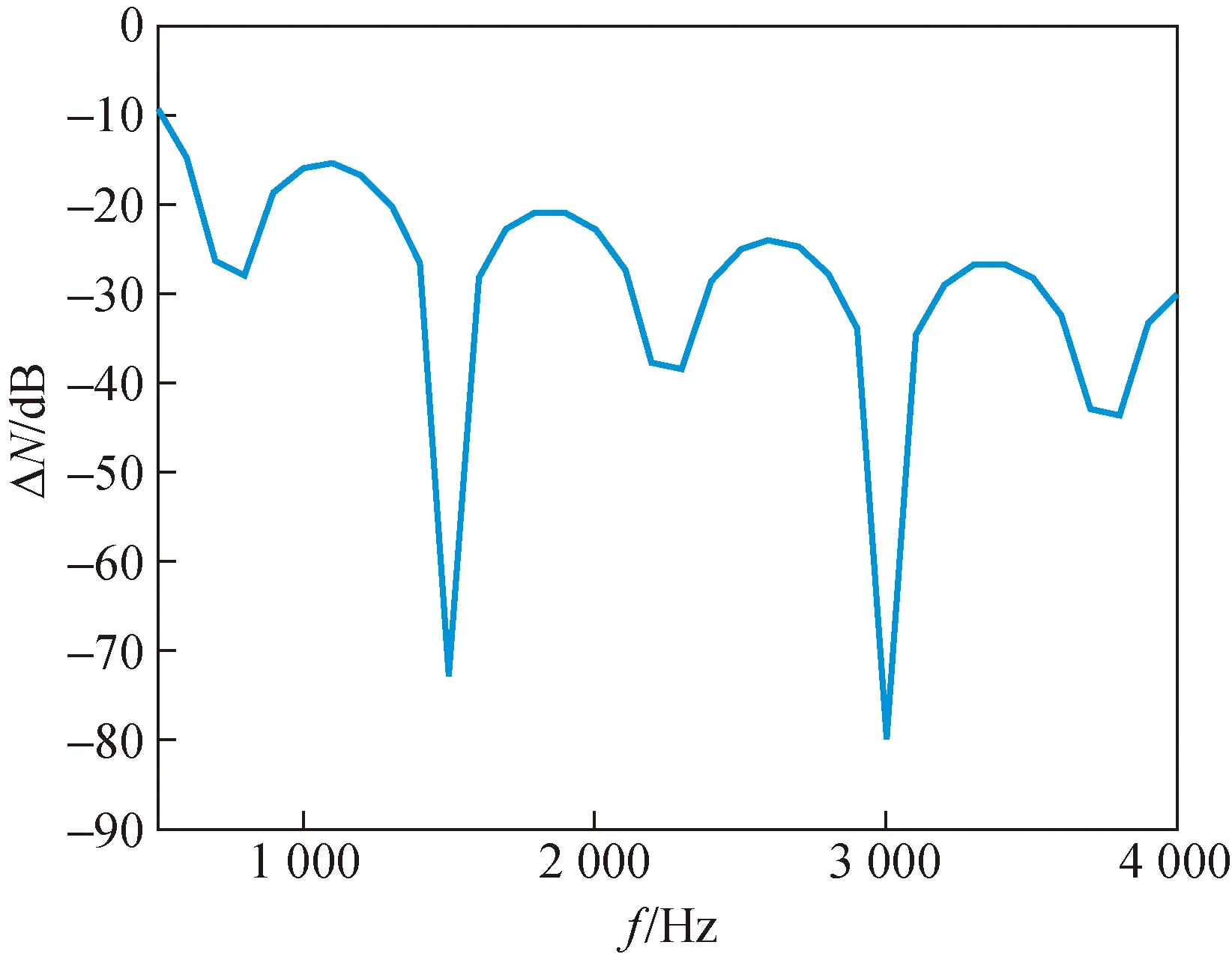
图4 重新采样的互易常数修正量曲线Fig.4 Resampled reciprocal constant correction curve
对于修正量函数自下而上给予合理范围的截取。截取方法选用最小极值点取前后两个相邻极小值点的平均值代入,可以得到最后的补偿曲线如图5。
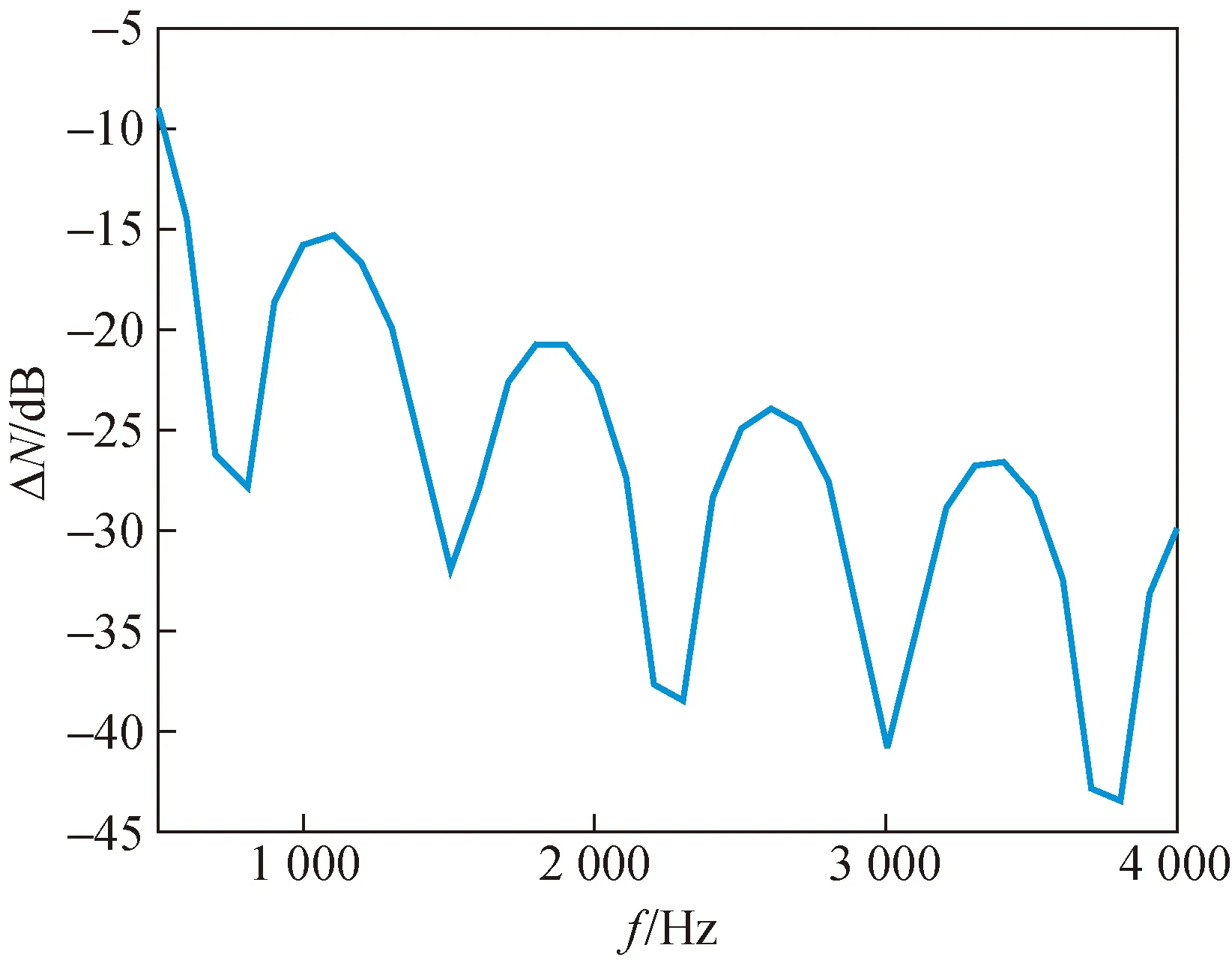
图5 截取后的互易常数修正量曲线Fig.5 Intercepted reciprocal constant correction curve
将互易常数修正量补偿到互易常数上,就可以得到补偿后的常数曲线。利用平面行波管中求灵敏度的公式,将补偿后的互易常数替换掉行波管中的固定常数,得到特定管中情况下的灵敏度值。
在低维空间中,欧式距离可以正确的表达数据的结构,所以在计算低维空间中的联合概率分布时直接使用欧氏距离,并沿用t分布将距离映射为概率:
4 实验过程设计
4.1 实验系统参数设计
管中校准法的高频极限取决于管子的直径[9]。当管子的直径超过管中声波波长的三分之一时,在管子的横截面上,声压分布受管的反射影响较大,不利于其他参数对声压影响的研究。因此结合波长与频率公式可以得到管子直径a满足以下条件:
(16)
已知水下声速c=1500 m/s,测量的频率在 5 kHz 以下,根据计算,管内直径最大可以达到 100 mm。在涉及到换能器校准方法的文献中均提出了接收换能器不能处于发射换能器的近场区,因此根据平面波区域的计算可以设置换能器之间的间距为30 cm。
4.2 实验测试系统的搭建
按照参数设计的换能器间距以及钢管的规格进行材料加工,得到一个间距为30 cm的三角支撑架以及一个内径为100 mm、厚度为5 mm的不锈钢钢管,三脚架用于根据特定的间距安装换能器并固定其位置,便于同时从管中放入与取出,钢管外包裹泡沫膜则是为了增加边界的阻抗值。
如图6所示3个换能器①②③分别对应发射换能器F、互易换能器H以及接收换能器J。其中,①、③为圆管换能器,②为小球换能器,固定在 30 cm 间距的三角支撑架上将换能器连同支撑架放入图7所示的钢管中,再将钢管放入长3 m、宽2 m、深3 m,四周带有吸声尖劈的消声水池中央,水深1.5 m的位置,进行测量。

图6 换能器及其固定装置Fig.6 Transducer and its fixing device

图7 测量管装置及布放Fig.7 Measuring tube installation and placement
根据参数设计等理论研究搭建了水下管中互易常数测量系统,实验系统如图8所示:包括不锈钢钢管,固定三角支撑架,圆管换能器,标准水听器,功率放大器,信号函数发生器,数字示波器等。
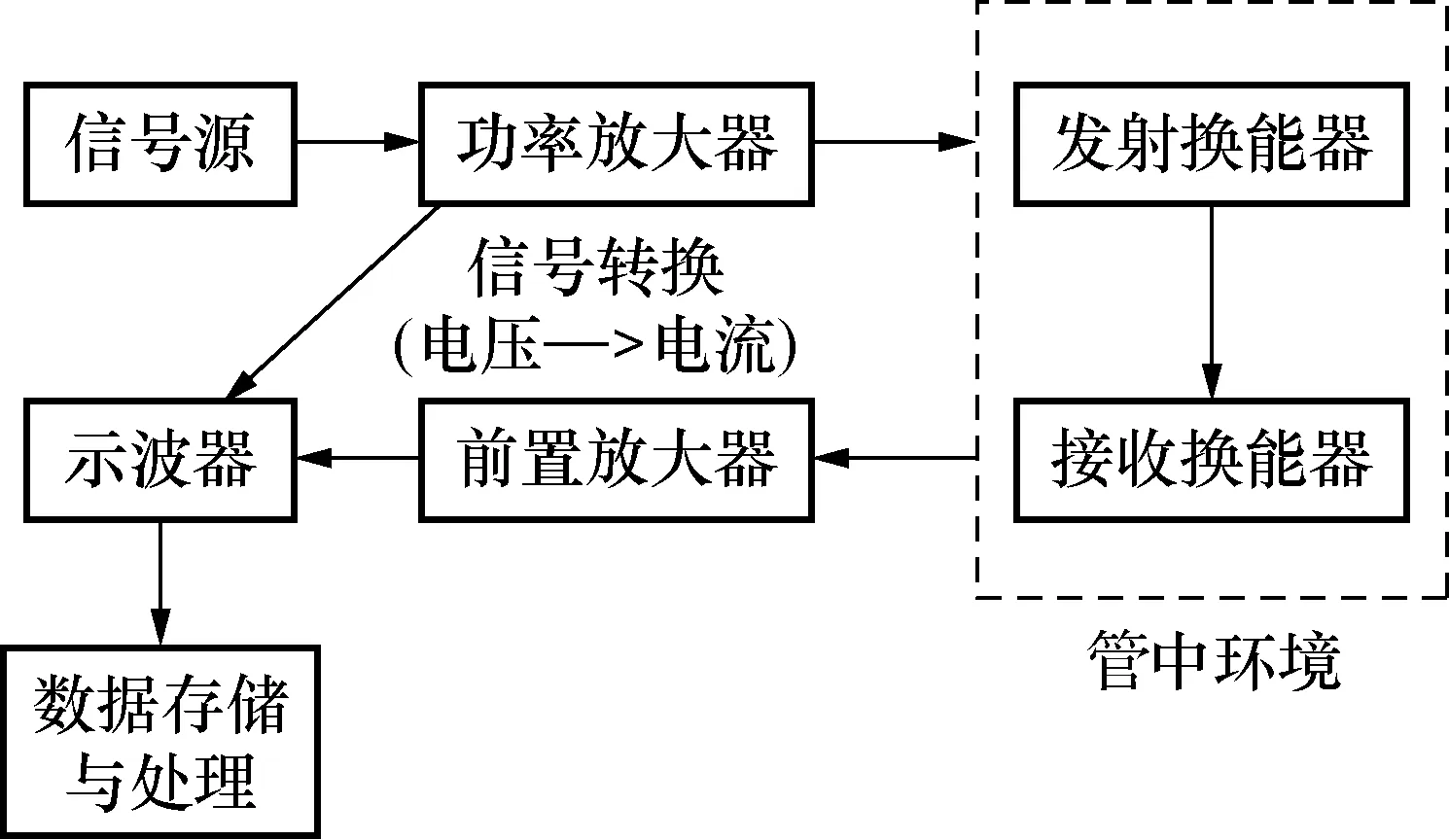
图8 实验测试系统流程Fig.8 Experimental test system flow
利用搭建的测量系统,基于如图9的互易法[17]测量步骤,对3个固定在三角支撑架上的圆管换能器进行3组激励电压与响应电流的测量,此时间距d为30 cm,采样频率间隔设为0.1 kHz,测量频率范围为0.5~4 kHz。

图9 互易法测试过程示意图Fig.9 Schematic diagram of the reciprocal method testing process
测量得到的数据进行计算得到相应的电压与电流值,结合理论推导的管中互易常数值,一同代入到公式(15)的灵敏度计算方法中,就可以得到互易换能器的灵敏度与灵敏度级曲线。
4.3 实验系统验证
运用COMSOL仿真软件对实验环境进行建模仿真,可以得到阻抗管中的声压变化规律。建立一个仿真模型如图10,水池外为完美匹配层,线列阵管为钢材料,管外包裹一层空气泡沫膜,管长为 1.3 m,管径为100 mm,将此模型在COMSOL中建立并求解。

图10 实验装置仿真模型Fig.10 Experimental device simulation model
此种边界条件情况下,管中接收点声波随频率的变化在0.75、1.5 kHz等处存在极值,有明显的浮动。浮动情况与后续实际实验搭建测得的管中电压值相一致,为后续的实验进行了初步的准备与相互验证。极值点与图3中公式计算出的奇点相符合,表现出在特定的管径、边界材料和管中布放情况下在这几个频率点确有声压的大幅变化,此情况的互易常数更需要补偿。
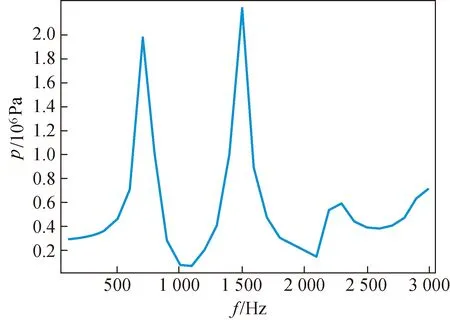
图11 仿真接收换能器的波形曲线Fig.11 Simulation of the waveform curve of the receiver transducer
5 实验测量与结果分析
5.1 自由场灵敏度测量
为了验证管中互易法的可靠性,先利用自由场比较法[18]对互易换能器进行灵敏度M的测量与计算,其基准值作为换能器性能的依据。步骤如下:首先将需要用到的换能器在水中充分浸泡,使用一个直径为30 mm的小球换能器作为声源,放置于水下1.5 m的深度,使用RESON标准水听器在距离声源30 cm的位置作为接收,得到一组发射电流与激励电压值;然后将标准水听器取出,将互易换能器放在标准水听器的位置,得到第二组信号值;最后代入标准水听器的标准灵敏度到比较法灵敏度级的计算公式中,对照标准水听器校准证书中数据,可以得到被测换能器的灵敏度级值,部分值见表1。从表1可以得到用作互易换能器的灵敏度dB值在-200左右。
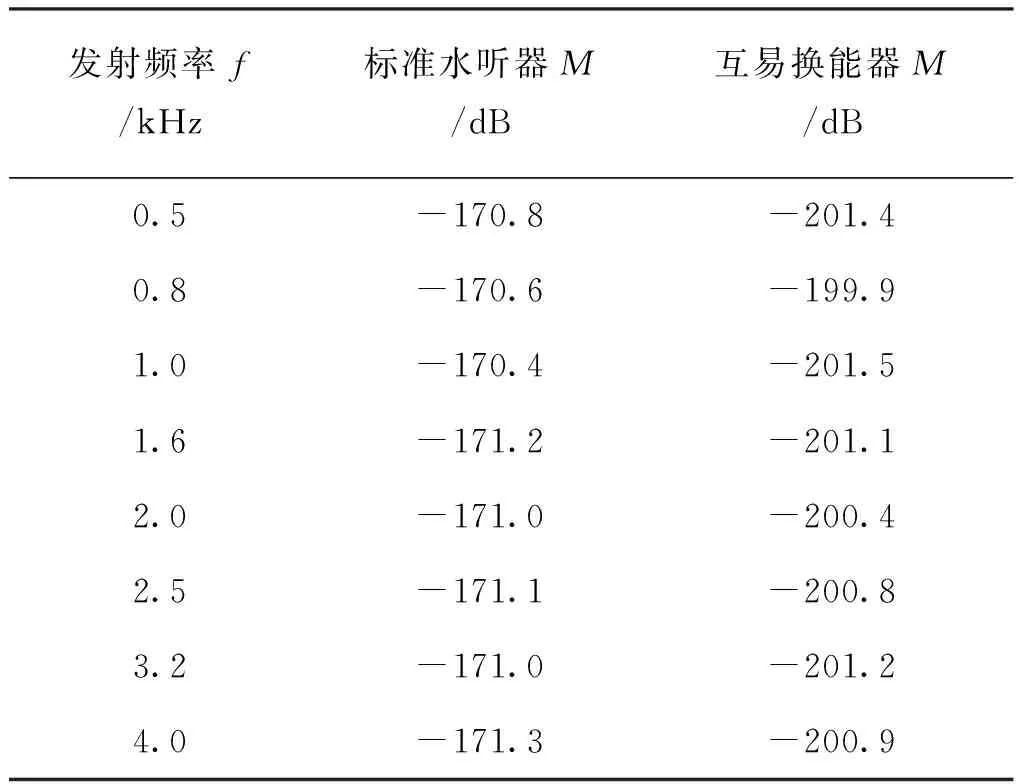
表1 自由场比较法的部分接收实验结果Tab.1 The free field comparison method partially receives the experimental results
由数据可以看到,使用自由场比较法测量圆管换能器的灵敏度在2 kHz以下的低频范围内波动幅度和误差值较2 kHz以上频率大,除了换能器本身的低频性能以外,主要原因可能为2 kHz以下频率的信号在自由场测量时由于信号衰减较快,造成信噪比不够,从而使测量值有一定的误差;而管中环境可以提高测量信噪比,有效排除这种误差,因此包裹在泥沙等类似管中环境的校准测量可以在低频测量中发挥其相应的作用。
由于管中测量发射信号为连续正弦信号,因此为了排除后续管中测量时电串等环境干扰,设置了一组自由场互易法实验,该实验使用相同的3个换能器和设备及连接线,在消声水池中发射脉冲信号进行测量。发射5个脉冲信号,经过排查,消除了主要的环境等干扰。测量结果经过自由场互易计算公式得到互易换能器的灵敏度如图12,测量频率范围为1.5~3 kHz,灵敏度的变化范围为0.89 dB。
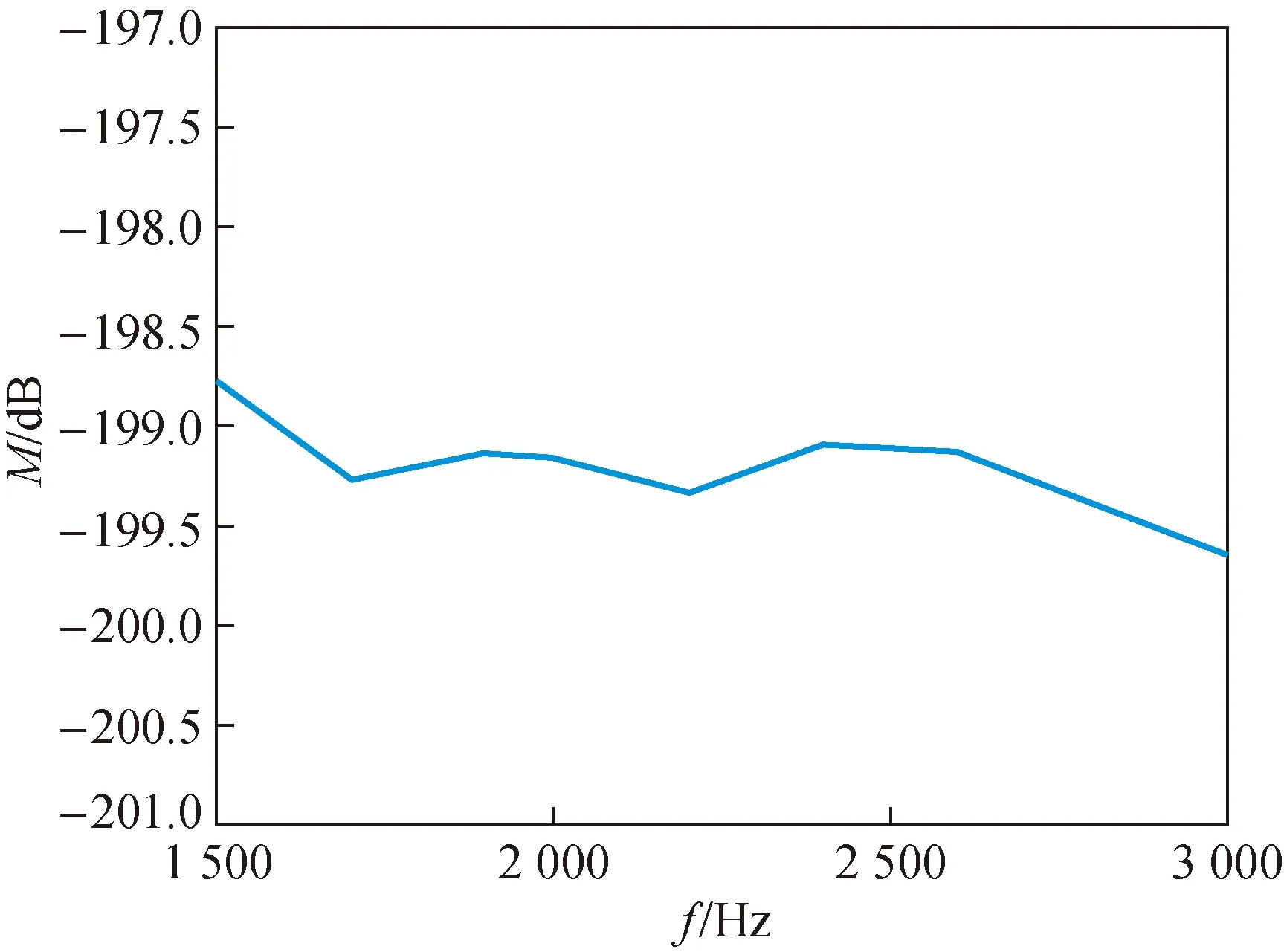
图12 自由场互易法测得换能器H的灵敏度级曲线Fig.12 The sensitivity level curve of the transducer H measured by the free field reciprocity method
5.2 管中互易法灵敏度测量
应用互易法测量得到的激励电压值UFH,UFJ,UHJ以及响应电流IH,分别将修正前和修正后的互易常数代入灵敏度公式,可以求得互易常数修正前后互易换能器的灵敏度。
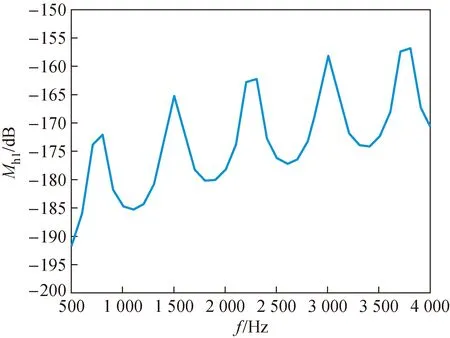
图13 修正前互易换能器灵敏度级曲线Fig.13 Sensitivity level curve of reciprocal transducer before correction
将实验测得的数据代入未修正互易常数的灵敏度公式求得的灵敏度值曲线如图14,发现使用管中测量法得到的互易换能器的灵敏度值变化较大,其中心值与自由场互易法测得的灵敏度级在数值上差别较大,因此需要将修正值代入。
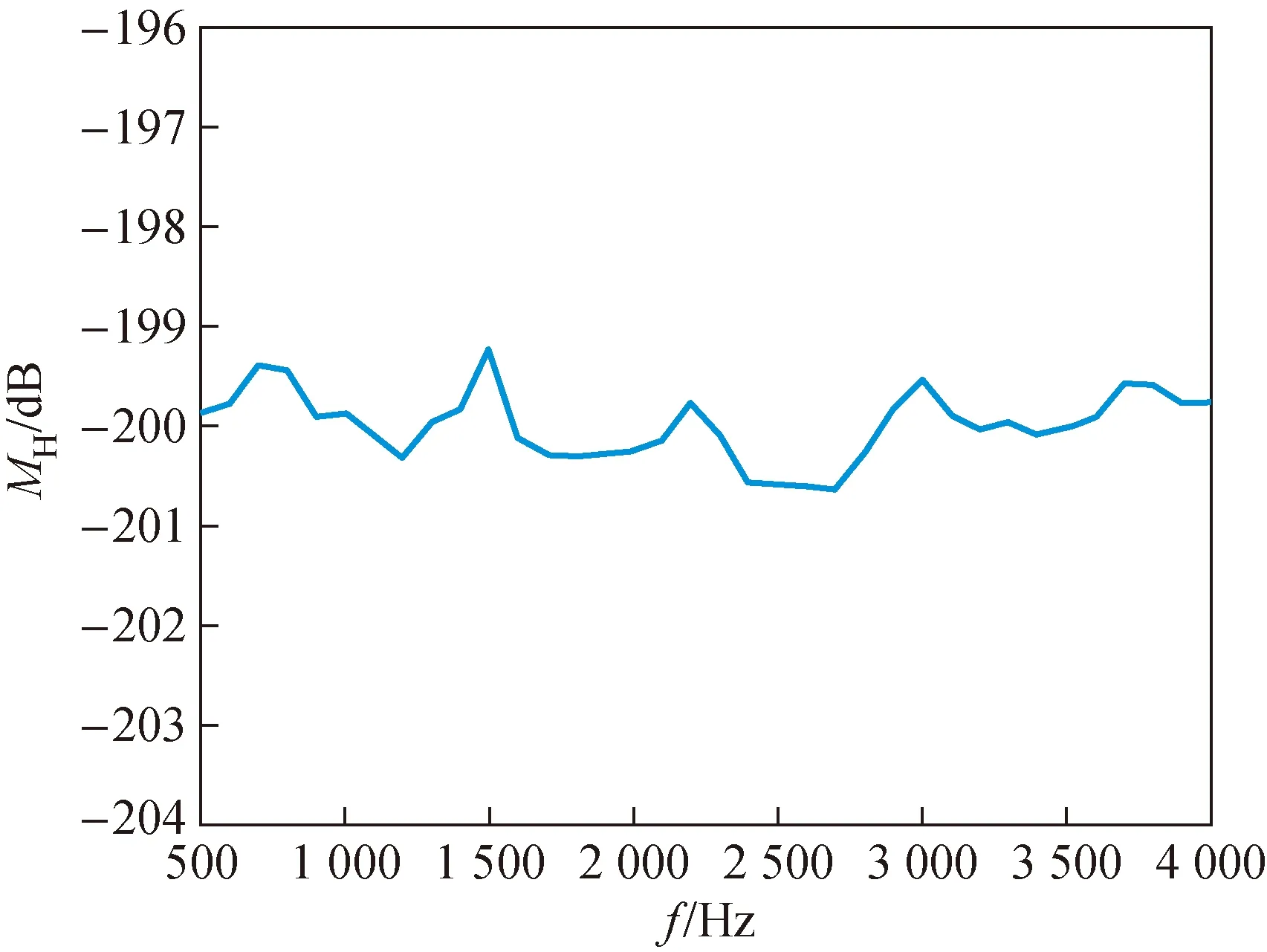
图14 修正后互易换能器灵敏度级曲线Fig.14 Corrected sensitivity level curve of reciprocal transducer
图14是将互易常数在修正量补偿后代入到灵敏度计算公式后的曲线图,量值十分接近自由场测得的灵敏度-200 dB,在0.5、1.5 kHz等频率点能明显看到补偿后的趋势,且补偿后的互易常数值代入得到的灵敏度更准确。在测量频率0.5~4 kHz范围内,可以得到换能器H的灵敏度的频响最大差值为1.41 dB,在1.5~3 kHz频率范围与自由场互易法测量误差最大为1.2 dB,误差在测量可接受的范围,验证了互易常数补偿的必要性和准确性。结果也可以看到,在1.5 kHz和3 kHz处灵敏度起伏相对其他频率大,除去这两个频率点后的曲线变化降为1.12 dB。
分析可知,这两个相对较大的误差值是在互易常数补偿时造成,因此在实验测量时尽量避开该奇点,会使灵敏度测量更加准确。
6 结 论
本文针对非刚性管中互易法的低频灵敏度校准,提出了一种基于管中互易常数修正的灵敏度校准方法,根据线列阵所处环境进行理论的边界条件及声压推导,得到特定非刚性边界环境下的互易参数值以及其修正量,利用仿真得到了随频率变化的互易常数值与修正量。搭建了实验系统并进行了对比实验,实验表明,经过修正的互易常数代入求得的灵敏度值比未修正的更加接近自由场比较法测得的灵敏度值,修正后求得的互易换能器灵敏度曲线在0.5~4 kHz频率范围内的最大起伏为1.41 dB,在 2 dB 以内,在此种测量环境中符合声学计量要求。对比仿真结果与实验结果,证实该推导合理可靠,验证了该方法的有效性和准确性。
通过对非刚性管中互易参数的推导及修正,可以使不同于密闭环境的低频灵敏度校准的管中校准成为新的校准方法,它具有较低的校准频率、方便快捷、测量条件宽松等优点。解决了自由场校准有着较高的低频下限问题,为海底泥沙下等非刚性环境中固定式线列阵的灵敏度检测与校准提供了指导。
