富水深厚砂层超深地连墙渗漏的示踪剂迁移过程模拟

于富来,王国林,于维鹤,张智军,东 盼,元熹翔,姜耘石,刘宏伟,田丰博

(1.中铁上海工程局集团市政环保工程有限公司，上海 201906；2.沈阳工业大学建筑与土木工程学院，沈阳 110870；3.西安石油大学地球工程与科学学院，西安 710065)

随着我国城市化进程不断加快，以往仅发展地面资源的道路难以实现可持续发展。为增强我国国民福祉，开发利用地下空间是一条有效的途径。在开发利用地下空间进程中，地下连续墙因具有刚度大、整体性能好的特点，在深基坑工程中受到广泛的应用[1]。目前，各学者利用各种模拟软件对基坑开挖过程分析较多，针对富水深厚砂层下的超深地连墙渗漏问题的有限元模拟较少。罗志华[2]对抽水试验过程中坑内外水位变化结果进行了数值模拟和分析，得到基坑围护、止水帷幕渗漏对抽水水位变化的影响规律；李琳[3]对基坑开挖和降水的模拟结果进行了比对，总结了基坑降水对深基坑变形的影响，并分析了地连墙存在漏水问题对基坑内外水位的影响。为判断地连墙上是否存在渗漏薄弱处，探寻渗漏点的存在对基坑内外渗流场的影响，建立了位于富水深厚砂层深基坑的二维有限元模型，模拟分析砂土中超深地连墙发生渗漏时现场实施墨水试验的可行性，探寻渗漏对地下水渗流的影响。

1 工程概况

1.1 地铁车站概况

该站为地下四层双柱三跨岛式车站，主体结构采用盖挖逆作法施工。该站主体标准段底板埋深33.55 m，盾构井段底板埋深35.45 m，较常规车站深约10～15 m，围护结构采用1.2 m厚地连墙，进行坑内降水，并辅以坑外泄压降水。

1.2 水文地质概况

该车站处地下水主要存在于中粗砂、砾砂土层中，属第四系孔隙潜水。设计初见水位埋深约为17.70～18.30 m，稳定水位埋深为16.50～17.00 m。基坑开挖范围内由上到下分别为杂填土、中粗砂层、砾砂层、圆砾层、粉质黏土层、砾砂层和泥砾层。

2 地下连续墙渗漏的有限元模拟

2.1 示踪剂迁移试验

为判断地连墙是否存在渗漏薄弱处，查清基坑内外地下水渗流路径，采用有色示踪剂进行示踪剂迁移过程模拟。因有色墨水在迁移过程中可始终保持性质稳定，故选用有色墨水作为示踪剂，在特定泄压井内压入高浓度墨水，使其作为溶质溶解在地下水中，以地下水为载体沿着渗流路径进行迁移，观察从相邻疏干井内抽出水的颜色，通过颜色变化情况判断相近地连墙是否存在渗漏点，为下一步采取有针对性的施工措施和降水井运行调度提供科学依据。

2.2 考虑渗漏影响的基坑二维有限元模型

采用有限元软件ABAQUS依据基坑施工现场情况建立二维流固耦合数值模型。在ABAQUS中设定多孔介质材料，基于总孔压进行建模，划分网格时使用特定的孔隙水压力单元，对模型进行稳态的线性渗流计算。计算时将有限元的网格固定在土体骨架上，地下水流过网格，地下水在渗流过程中满足二维非稳定流的渗流运动方程。地连墙渗漏模拟共4个分析步[4]，依次为初始分析步、地应力平衡分析步、渗漏分析步、降水分析步。

3 计算结果分析

3.1 抽水及示踪剂迁移过程模拟

通过ABAQUS软件建模分析，模拟坑内的疏干井持续抽水时，将坑外其它泄压井关闭，向特定泄压井内注入有色墨水，得到当地连墙完整情况下的水流速度矢量(图1)及存在渗漏情况下的水流速度矢量(图2)。从图2中可以看出，渗漏点的存在使坑内外产生了水力联系，形成水头差，处于坑外地下水中的有色染色剂会以地下水为载体渗入到基坑内部，从疏干井内被抽出，验证了使用示踪剂迁移试验在实际工程中判断地连墙渗漏的可行性。

3.2 渗漏点破坏程度对基坑渗流场的影响

改变渗漏点的渗透系数，将渗漏点渗透系数从2.5×10-4m/h扩大至2.5 m/h时，坑外水位从每天下降0.29 mm增加到每天下降260 mm，坑内水位从每天上升0.86 mm增加到每天上升610 mm，渗漏速度与地连墙渗漏程度呈正相关。当渗漏点的渗透为2.5×10-4m/h时，坑外水位每天下降0.29 mm，坑内水位每天上升0.86 mm，继续减少渗漏点的渗透系数，水位变化不再明显。

当渗漏点的渗透系数k≥0.25 m/h时，坑外孔隙水压力随时间变化呈凹形，坑内孔隙水压力随时间变化呈凸形，内外水位变化会随着时间的推移而逐渐变缓，其原因是渗漏点的渗透系数大，即地连墙破坏程度大，坑内疏干井的出水量小于从坑外涌入坑内的进水量，坑内水位上升，坑内外水头差减小，导致坑外地下水涌入坑内的速度变缓。当渗漏点的渗透系数k<0.25 m/h时，其孔隙水压力随时间变化呈直线形。因地连墙的破坏程度较小，渗漏点在短期内对基坑内外的水头差的影响较小，渗漏速度几乎不发生改变。

3.3 渗漏点尺寸对基坑渗流场的影响

渗漏尺寸与坑外侧形成漏斗面积呈正相关，漏斗形状随着渗漏尺寸的增大而逐渐明显。相同条件下，不同渗漏尺寸下孔压变化规律大致相同。尺寸大小与涌入基坑内的地下水含量呈正相关。渗漏尺寸为0.8 m时，坑外孔压变化量是渗漏尺寸为0.3 m时的1.75倍；以渗漏尺寸0.8 m为例，随着时间的变化孔压变化速度从0.524 Pa/s降低到0.083 Pa/s，水位下降速度随着坑内外水头差的减小而逐渐趋于平缓。

3.4 渗漏点深度对基坑渗流场的影响

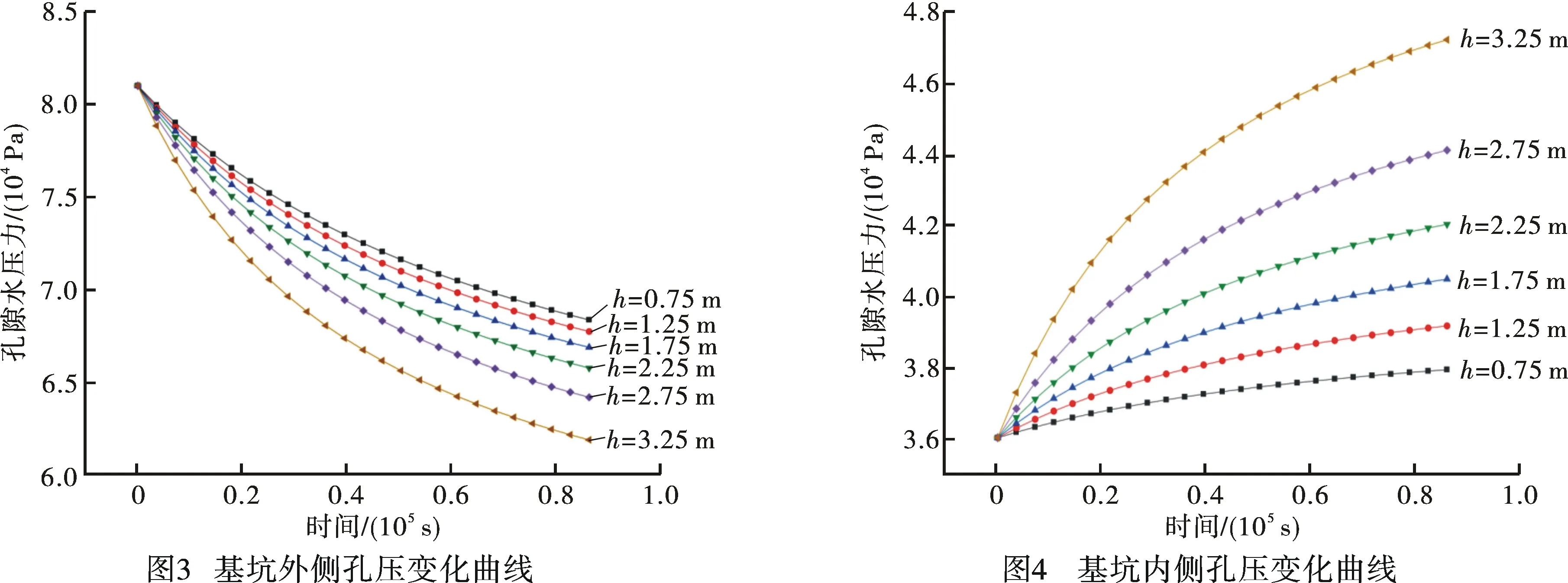
渗漏点所处地连墙的位置同样会导致坑内外水位变化规律的改变。渗漏点所处位置不同对坑内外孔压变化的影响如图3、图4所示。通过比对可以发现，地下水向基坑内渗漏速度与渗漏位置的深度总体呈正相关。当渗漏点位置从距坑内水位以下0.75 m增加到3.25 m，坑外孔压下降量增加了6.469 9 kPa；坑内孔压上升量增加了9.278 kPa。坑外孔隙水压力变化曲线均为凹形，坑内外的凹、凸形曲线是由于渗漏导致水头差的减小导致的。渗漏点不同位置对坑内外孔压变化影响规律一致，且随着渗漏位置的加深，孔压变化量呈上升趋势。

3.5 地连墙渗漏条件下渗漏点后续破坏分析

当地连墙存在渗漏点时，从坑外源源不断涌入坑内的水会对渗漏点产生进一步破坏。模拟分析结果表示，地铁车站基坑模型渗漏点处地下水流速最大，且渗漏点上侧流速约为下侧流速的1.1～1.3倍。

随着渗漏点位置的变化，渗漏点的最大流速和最小流速也随之变化，最大流速、最小流速均与渗漏点所处深度呈负相关，但最大流速变化量会随着渗漏点深度的增加而逐渐趋于平缓，最小流速变化量则会随着渗漏深度的增加而越发陡峭。

将渗漏点上下两侧流速差值随渗漏点深度变化绘成曲线，流速差值与渗漏点位置曲线总体呈凹形，且存在流速差值最小位置。对数据进行拟合分析，得到拟合曲线如图5所示。

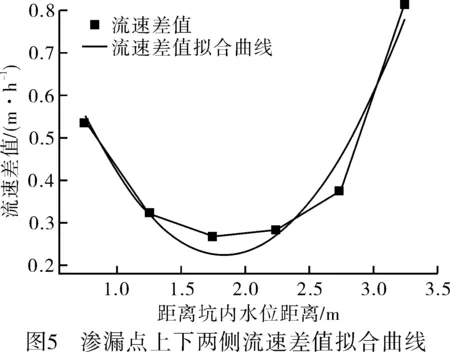
由拟合曲线可知，渗漏点部位上下两侧流速差值随渗漏点位置的降低，呈现先降低后升高的趋势，在位于坑内水位以下1.84 m时达到最小，为0.228 m/h；位于坑内水位以下3.25 m时达到最大，为0.778 m/h。由此可以判断，距离坑内水位小于1.25 m的渗漏点和距离坑内水位超过2.75 m的渗漏点，渗漏产生的后续破坏，其上侧破坏程度要大于下侧破坏程度，且渗漏点在距坑内水1.84 m处时上下两侧的破坏情况较为均匀。

4 结 论

论文依据沈阳某地铁工程，利用ABAQUS建立处于富水深厚砂层的地铁车站基坑模型，结合工程现场实际问题，判断了示踪剂迁移试验在判断地连墙渗漏问题上的可行性，研究了渗漏点各因素对基坑内外渗流场的影响，提出渗漏治理措施。

a.通过向地连墙外侧的降水井注入有色染色剂，通过观察疏干井抽出的地下水颜色变化可以作为判断地连墙是否存在渗漏的一种方法。

b.当地连墙存在渗漏时，渗漏速度与渗漏程度呈正相关。当渗漏点的渗透系数为2.5×10-4m/h时，坑内外水位单天下降量均远小于1 mm，继续减少渗漏点的渗透系数，水位变化不再明显。可将渗透系数2.5×10-4m/h作为衡量地连墙堵漏施工是否有效的标准。

c.渗漏尺寸大小与漏斗面积呈正相关。渗漏尺寸为0.8 m时坑外孔压变化量是渗漏尺寸为0.3 m时的1.75倍。故现场水位检测数据若出现异常且变化幅度较大时，可以考虑是否因附近地连墙产生了尺寸较大的渗漏点，导致附近水位变化异常。

d.水位之下渗漏点的深度与地下水渗漏速度呈正相关。基坑内外地下水渗漏的速度会随着水头差的减小逐渐趋于平缓。现场可通过坑内外水位变化情况初步确定地连墙是否存在渗漏点以及渗漏点的可能标高。

e.地连墙存在渗漏时渗漏点处地下水流速最大且渗漏点上侧的地下水流速约是下侧地下水流速的1.1～1.3倍。渗漏点上部的渗漏程度将更加严重。在对渗漏点进行补漏时，应对渗漏点上部进行额外加强处理，渗漏点所处位置越深，越应予以重视。