基于主成分分析和改进Bayes判别的岩爆等级预测
2022-10-20周宗红洪贞群
刘 剑,周宗红,刘 军,洪贞群
( 1. 昆明理工大学 国土资源工程学院,云南 昆明 650093;2. 元阳县华西黄金有限公司,云南 红河 661400 )
岩爆是深埋地下工程的地质灾害之一,对人员、设备和国家财产造成巨大的威胁。近年来,我国深部地下工程逐年增多,岩爆灾害也呈频发趋势[1-3]。
目前,相关学者从不同的方向对岩爆进行预测研究,提出了许多对岩爆烈度的预测方法。蔡美峰[4]等基于开挖扰动能量积聚理论,对三山岛金矿未来深部开采过程中可能诱发岩爆的地点和等级进行预测;陈炳瑞[5]等研发了传感—采集—传输一体化集成、32位A/D与元器件联合降噪和微震信号递归神经网络识别等技术,使微震监测技术朝着岩石工程灾害自动监测、分析与智能预警方向快速发展;李克钢[6]等提出一种基于改进综合赋权的岩爆倾向性评价方法,选取应力条件和围岩对应的15个因素作为岩爆倾向性指标,判断岩爆倾向性等级与可靠性;李宁[7]等建立了粗糙集理论和粒子群支持向量机( RS-PSOSVM )的岩爆预测模型,并将该模型用于大相岭隧道岩爆的预测;吴顺川[8]等基于PCAPNN原理建立岩爆预测模型,在保证预测精度的前提下提高收敛速度;汤志立[9]等基于9种经典机器学习算法建立岩爆预测模型,并应用于西藏多雄拉隧道的岩爆预测;谢学斌[10]等基于CRITIC-XGB算法建立岩爆倾向性预测模型,为岩爆倾向性等级预测提供一种新的可靠方法;周科平[11]等采用熵权法和云模型判定岩爆等级,建立熵权-正态云模型并应用于公路隧道工程中;王佳信[12]等基于PCA-DDA建立冲击地压的判别模型,对复杂的地质灾害进行预测。
虽然相关学者对于岩爆进行了大量研究并取得了一定成果,但是岩爆的机理十分复杂,采用数学或者力学的方法很难达到准确的预测精度。
近年来Bayes优异分类性能受到广泛关注,付玉华[13]等基于Bayes判别选取4个指标对岩爆进行了预测;宫凤强[14]等提出了地下工程岩爆发生及烈度分级预测的Bayes判别分析方法。上述岩爆预测理论都取得了较好的预测结果,但考虑到岩爆样本所属类别分布不均衡,导致了Bayes判别在决策边界附近出现误判,降低了判别的准确率。笔者提出了基于阈值改进的Bayes判别模型,在考虑到数据样本的先验概率和错误损失的前提下,不断更新先验概率的值,进而求得后验概率。设置后验概率的阈值来消除决策边界附近分类不确定性的风险。分类边界处通过最大后验概率判别存在较大误判风险,基于阈值改进的Bayes判别可以消除误判风险,提高判别的正判率。
1 主成分分析和阈值改进Bayes理论
1.1 主成分分析法理论
主成分分析是一种通过降维技术把多个变量转化成几个主成分的多元统计学方法,得到的主成分能够反映原始变量的大部分信息,通常表示为原始变量的组合。为了达到主成分所包含的信息不重叠,要求各成分之间互不相关[15]。设有p个变量第i次试 验 中的 取值 为得到原始矩阵为
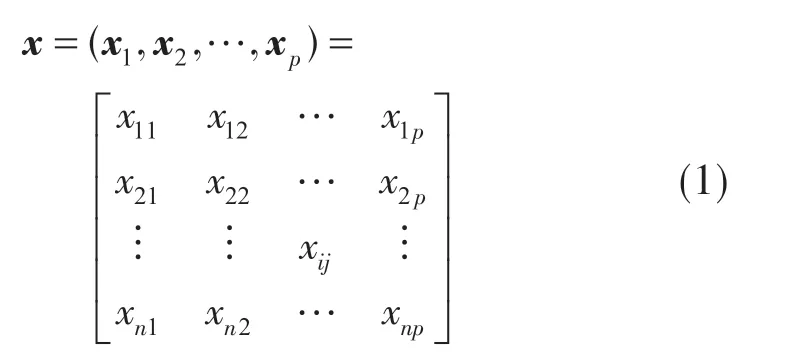
步骤1:计算xij*标准差。
主成分分析的结果易受量纲影响,为了消除量纲对变量的影响,先把各变量的单位标准化得到矩阵x*。xij*为矩阵x*的一个数,计算公式为

式中,为变量xj的观测值的平均值;sjj为变量xj的观测值的方差;为标准差。
步骤2:计算相关系数矩阵R。

和rpo为对称矩阵,指标间相关系数rop计算公式为
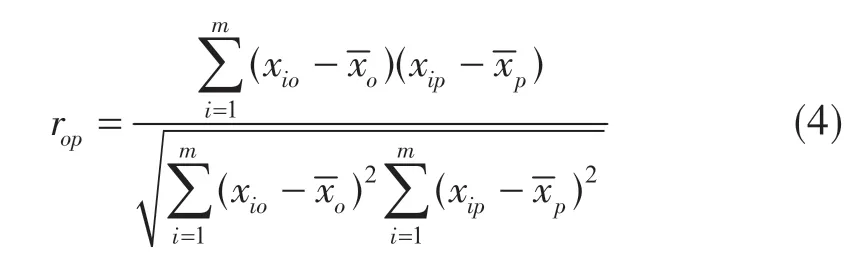
步骤3:确定主成分个数。
通常特征值大于1,累计方差贡献率大于80%,特征值记为λ1,λ2,…,λn,方差贡献率vs和累计方差贡献率vt计算公式分别为
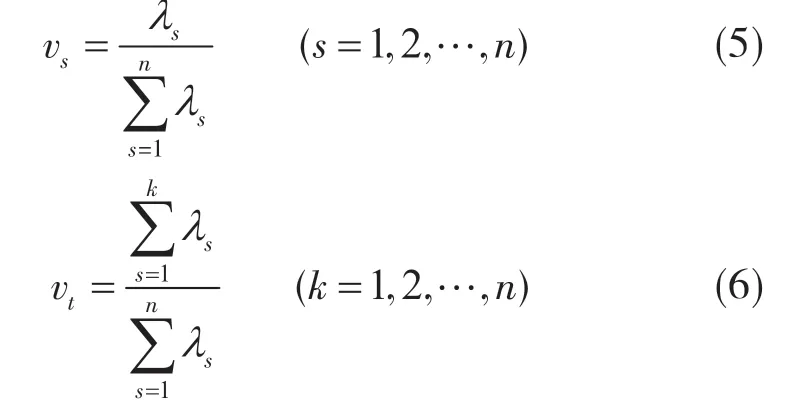
步骤4:计算提取主成分的对应得分。
其中主成分系数矩阵为U=(p1,p2,…,pn),若提取k个主成分得分
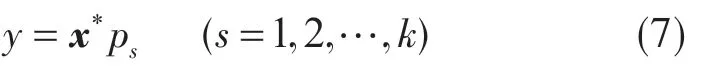
1.2 改进的Bayes判别理论
k组p维数据沿某个方向投影,投影需满足组与组之间尽可能分开的条件[16]。
先验概率ip计算公式为

式中,nω为类别属于ω的样本数量为样本总体。
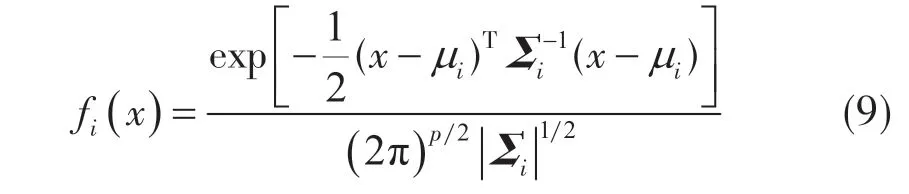
式中,iμ为第i个总体的均值;iΣ为协方差矩阵。
根据Bayes理论,样品X来自总体Gi的后验概率,计算公式为

在不考虑误判代价的情况下,判别规则为
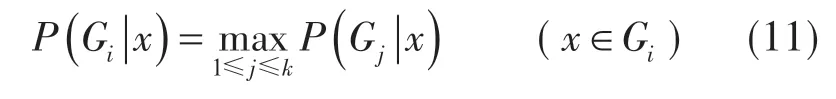
Bayes判别分析模型是根据已知分类标记的训练样本集构建一个分类器,然后根据构建好的分类器对已知属性和未知标记的数据进行分类。根据最大后验概率原则,确定最终的分类。Bayes判别分析模型在两个类别决策边界附近,属于该类的决策有很大的不确定性,易出现误判现象。本文通过设置警戒值,在分类边界处寻找一个阈值,作为Bayes判别分析模型有效性的标准,当后验概率大于阈值时,可以认为最大后验概率分类有效;当后验概率小于阈值时拒绝分类,表明该样本后验概率位于分类边界附近,分类具有较大的风险。
考虑到Bayes判别先验概率差距较大时,对后验概率分类造成较大影响,根据先验概率差距大造成误判的现象,提出一种按先验概率比例来确定阈值的方法,先验概率比例系数kj的计算公式为
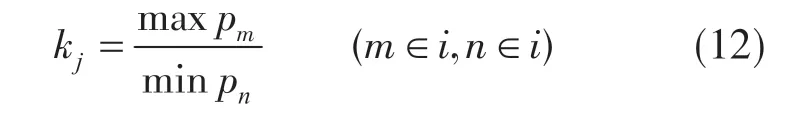
式中,i=1,2,3,4;mp和np分别为1级、2级、3级和4级先验概率;maxmp为最大先验概率;minnp为最小先验概率。
当样本数据各类别为相等数量时,各类别先验概率相等,kj=1。
后验概率比例系数计算公式为
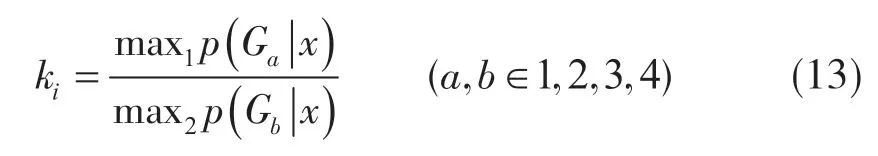

式中,Ω为阈值,即后验概率临界值。
kj>ki拒绝判别;k j<ki接受判别;当时,拒绝判别;当时,接受判别。
当设Ω=1时任何决策都会被拒绝,当Ω过小( 样本个数的倒数 )时,所有样本的决策都不会被拒绝,无法提高模型的泛化能力。
2 基于阈值改进的Bayes判别岩爆等级综合预测模型
2.1 阈值改进Bayes判别评价步骤
阈值改进Bayes判别预测模型是一个综合评判岩爆等级的模型,通过主成分分析消除信息重叠对Bayes判别分析的影响,建立改进的Bayes判别模型。通过阈值判断后验概率的有效性,相较于传统的Bayes判别分析,拒绝了岩爆决策边界的附近分类( 分类决策有很大不确定性 ),提高了模型的正判率。基于阈值改进的Bayes判别综合预测模型流程如图1所示。
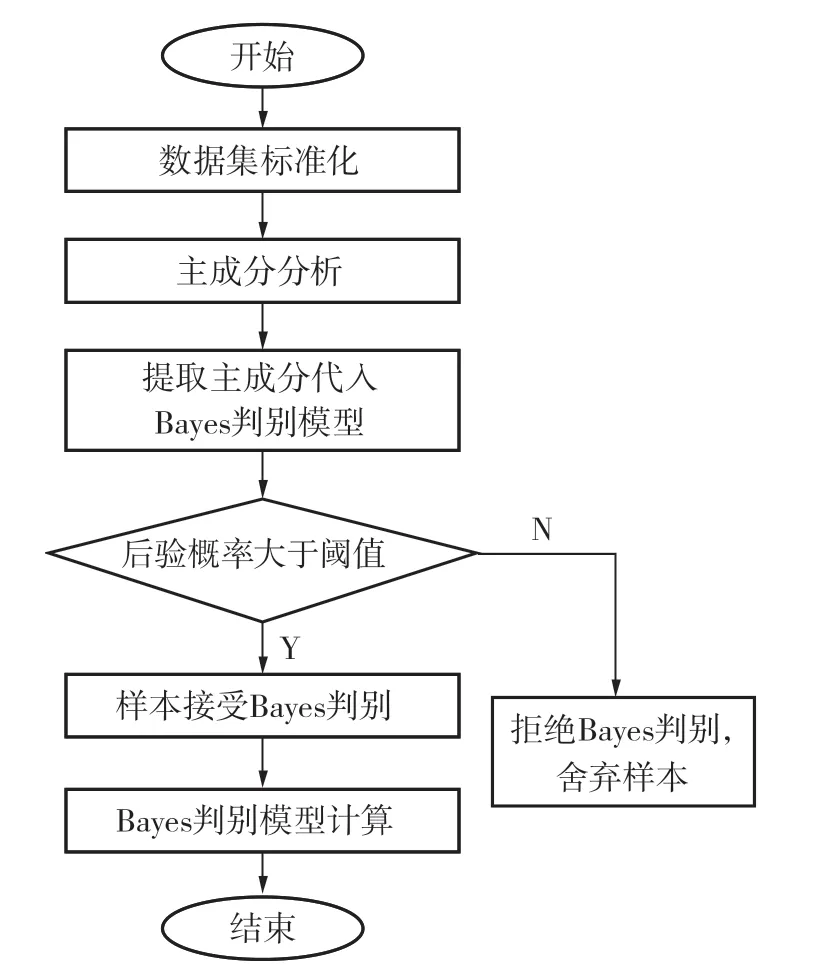
图1 阈值改进Bayes判别综合预测模型流程Fig. 1 Flow chart of Bayes discriminant synthesis prediction model is improved by threshold value
2.2 建立岩爆倾向性指标体系
岩爆发生的机理十分复杂。影响因素较多,主要包括岩体条件、应力水平、开挖方法、工程埋深及岩体的储能情况等。相关学者[2,17]研究发现,岩爆易发生在应力集中程度较高、高储能和完整的脆性硬岩中,主要破坏形式为张拉破坏、伴随剪切破坏( 抗剪记录较少,无法进行分析 )。其中围岩最大切应力( Maximum Tangential Stress,MTS )和应力集中系数( Stress Concentration Factor,SCF )能够反映围岩应力集中程度;单轴抗拉强度( Uniaxial Tensile Strength,UTS )能够反映岩爆断面破坏形式;单轴抗压强度( Uniaxial Compressive Strength,UCS )能够反映岩石的坚硬程度和完整性;脆性系数( Brittleness Index,BI )能够反映岩石的脆性大小,弹性能量指数( Elastic Energy Index,EEI )能够反映岩体储存和释放能量的性能。故本文选取以下6个指标:围岩最大切应力( MTS )、单轴抗拉强度( UTS )、单轴抗压强度( UCS )、应力集中系数( SCF )、脆性系数( BI )和弹性能量指数( EEI )等作为岩爆等级预测的评价指标,并按岩爆烈度由弱到强分为4个等级[17],分别为无岩爆( 1级 )、弱岩爆( 2级 )、中等岩爆( 3级 )和强岩爆( 4级 )。依据所选指标整理出典型岩爆工程案例数据[18-24],见表1。
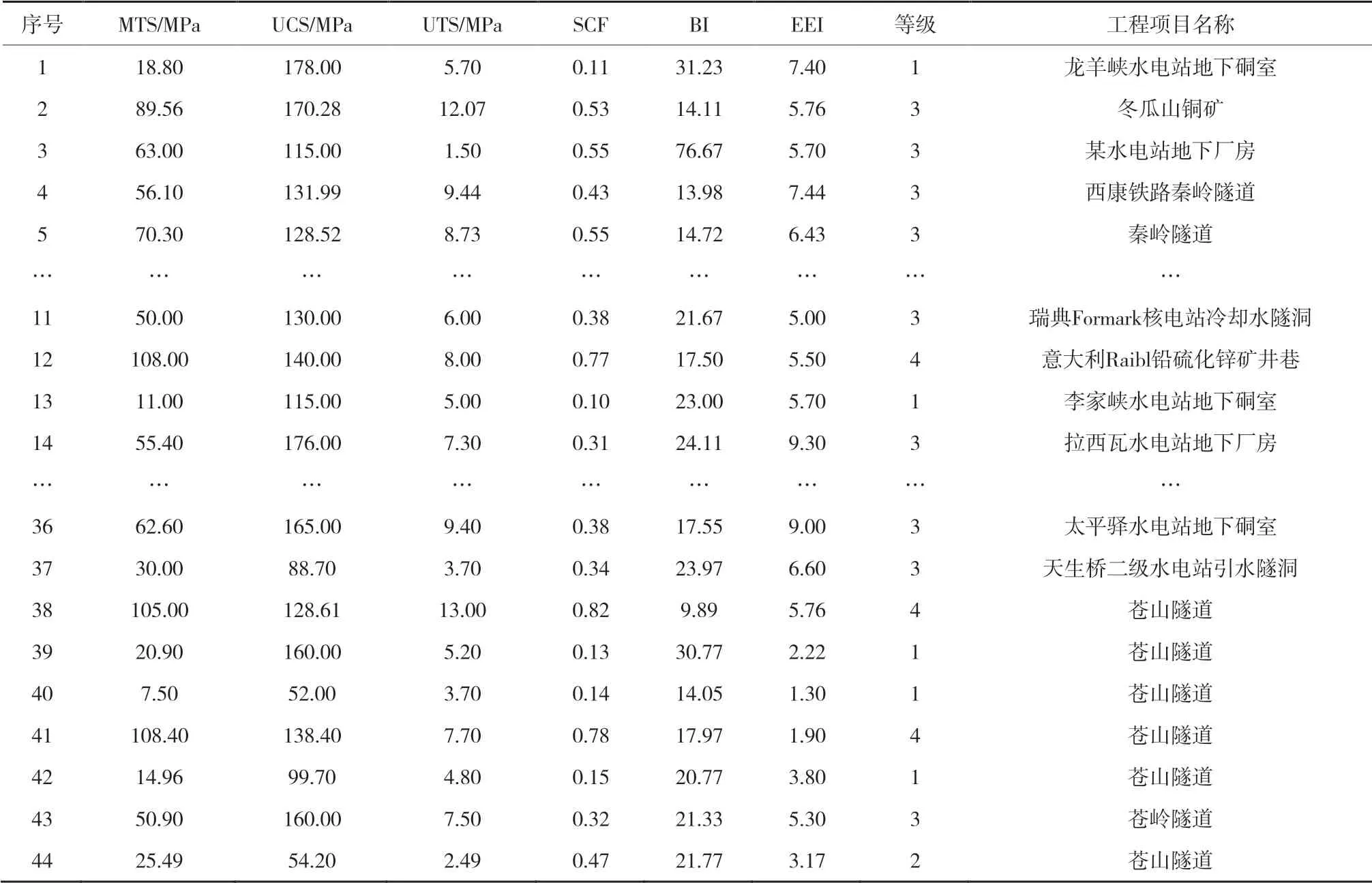
表1 实测岩爆实例数据Table 1 Actual data of rockburst
2.3 主成分分析法结果分析
为了消除指标量纲对模型判别精度的影响,对表1所列44组数据进行标准化处理。各指标的相关系数见表2。

表2 各指标相关系数Table 2 Correlation coefficient of each index
由表2可知,部分指标的相关系数大于0.5,从而使得指标之间信息重叠,有较为明显的相关性,所以采取主成分分析法消除指标之间的相关性,消除非独立性对Bayes判别模型影响,提高岩爆预测模型的准确性。
将标准化后的数据进行主成分分析,其累计方差贡献率见表3。

表3 累计方差贡献率Table 3 Cumulative variance contribution rate
由表3可知,前3个主成分累计方差贡献率为86.719%。国内外学者认为累计方差贡献率大于80%和特征值不小于1( 图2 )的主成分指标能充分取代其他指标,可以将计算得出的3个主成分Y1,Y2和Y3作为岩爆综合预测模型的指标。
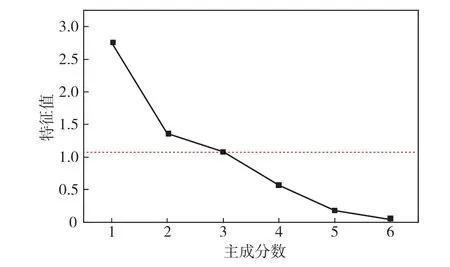
图2 主成分分析碎石Fig. 2 Principal component analysis of lithotripsy
主成分Y1,Y2和Y3与6个岩爆指标关系式为
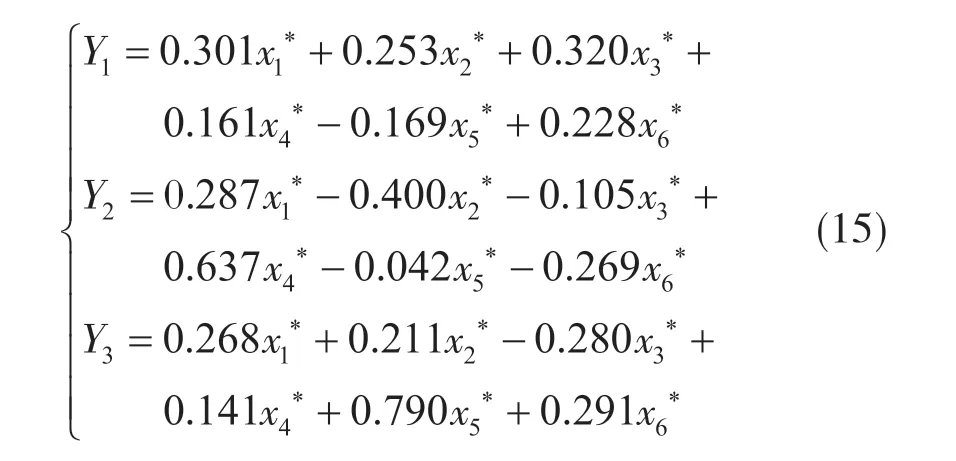
由式( 15 )可以看出,3个主成分可以充分代表围岩最大切应力( MTS )、单轴抗压强度( UCS )、单轴抗拉强度( UTS )、应力集中系数( SCF )、脆性系数( BI )和弹性能量指数( EEI )6个指标的绝大部分信息。
2.4 改进Bayes判别分析
将主成分分析的岩爆指标数据代入Bayes判别,进行岩爆倾向性等级评价。但考虑到Bayes判别模型在分类边界上受先验概率影响,位于分类边界附近,易出现分类错误,如图3所示拒绝区域内样本最大后验概率差距较小,位于分类边界附近。笔者提出一种通过阈值改进Bayes判别方法,提高Bayes判别的准确性和不同工况条件下岩爆预测的泛化能力,克服传统Bayes决策边界决策不确定性的缺点。阈值的确定会根据样本数量做出动态调整。
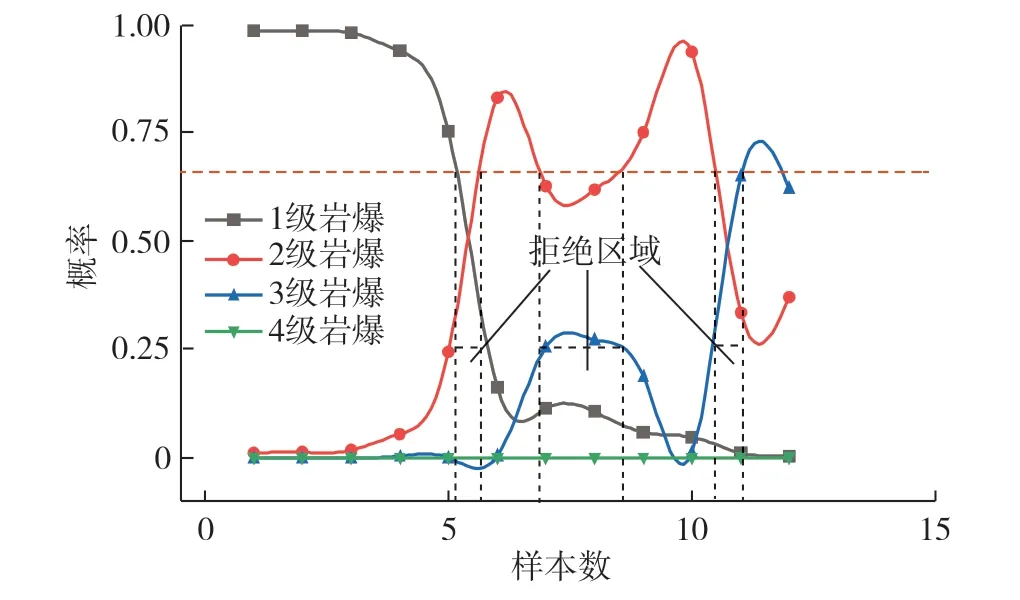
图3 Bayes判别的岩爆预测部分数据Fig. 3 Partial prediction data of rockburst based on Bayes discrimination
根据式( 8 )计算得出1级岩爆、2级岩爆、3级岩爆、4级岩爆的先验概率分别为0.205,0.114,0.500,0.182,代入式( 12 )计算出kj为4.4。Bayes计算出44组岩爆数据,将该数据分别代入式( 13 )计算出ik,按照判别规则式( 14 )筛选出后验概率位于分类边界数据,见表4。由表4分析发现,当kj>ki时拒绝判别,造成岩爆分类样本部分数据损失,如表4所示数据为决策边界附近舍弃样本。岩爆数据集各类别的样本数通常是不均衡的,造成先验概率差距较大,一部分样本后验概率处在分类边界处。
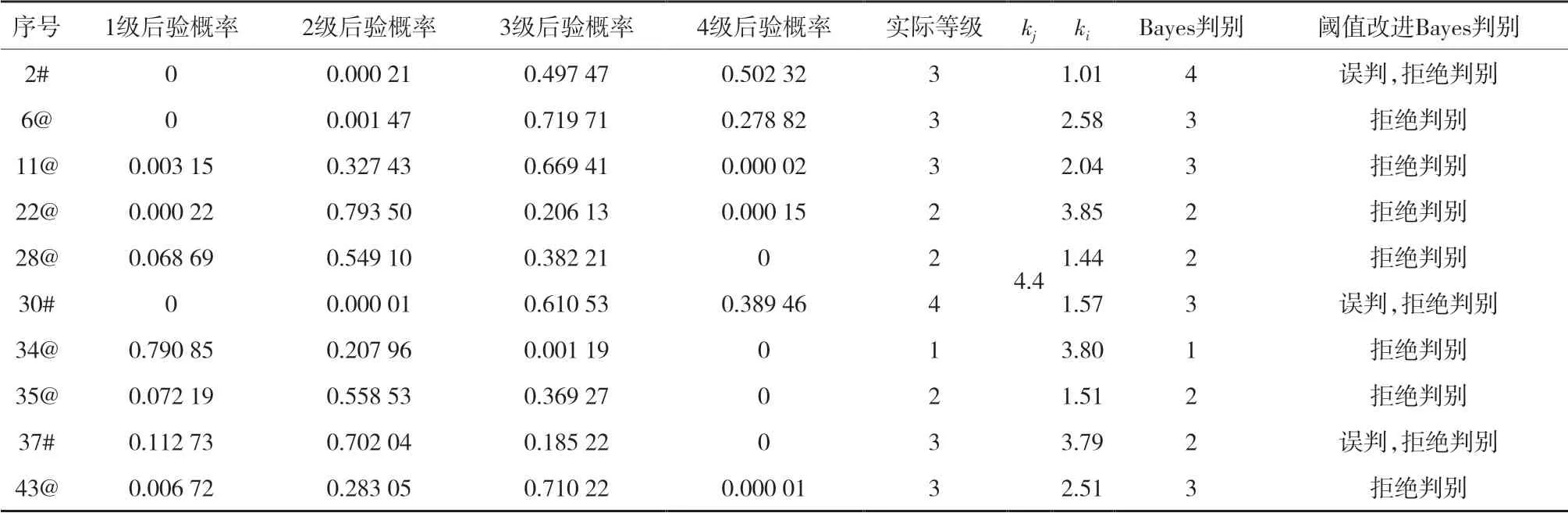
表4 决策边界附近的样本Table 4 Samples near the decision boundary
如图4所示,岩爆倾向性等级评价模型准确率为93.18%,考虑到一些样本数据类别后验概率差距较小,最大后验概率方法划分类别存在不足,即使在本次岩爆分级试验中分类正确,当调整岩爆数据集各类别的样本数时,出现在分类边界上样本易发生误判。因此笔者提出阈值改进Bayes判别,对于不满足阈值样本拒绝分类,阈值改进Bayes判别预测结果如图5所示,表明岩爆倾向性等级评价模型预测结果与实际相符。极大提高了岩爆倾向性分级的准确性。
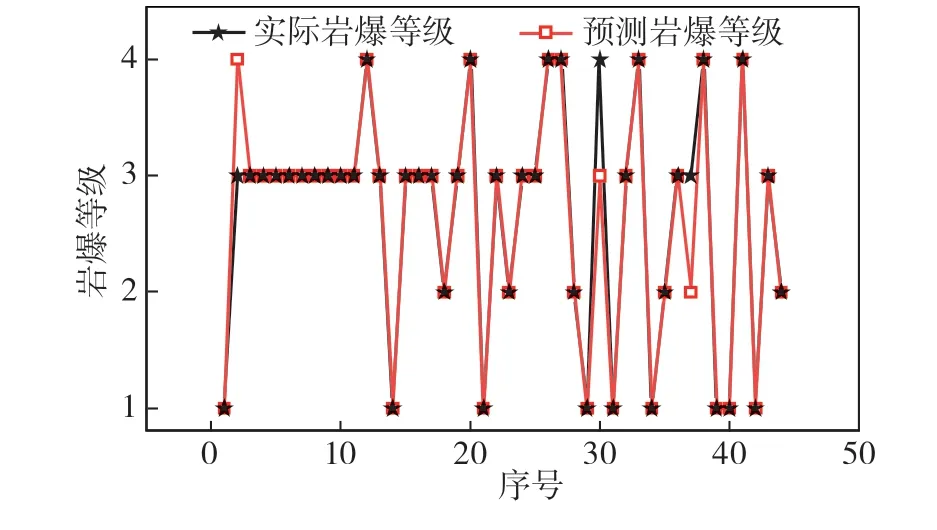
图4 Bayes岩爆预测等级Fig. 4 Bayes rockburst prediction grade

图5 改进Bayes岩爆预测等级Fig. 5 Improved Bayes rockburst prediction grade
2.5 岩爆预测模型敏感性分析
为了验证待测样本所属类别分布是否均衡,避免存在先验概率差距较大,从而造成岩爆预测模型准确率下降;同时避免样本和样本数量选择主观性的影响,本文分别根据表1随机选取样本,所属类别最少样本数量与所属类别最多样本数量之比按照1∶1,1∶2,1∶3,1∶4,1∶5和1∶6的比例代入岩爆预测模型和阈值改进岩爆预测模型。
图6为样本数量对预测模型的影响,由图6可知,随着样本比例增大,越来越多的样本后验概率处于分类边界附近,岩爆预测模型准确率随之下降,阈值改进后岩爆预测模型准确率明显提高。样本比较小时阈值改进模型改善效果不明显。

图6 样本数量对预测模型影响Fig. 6 Influence of sample size on prediction model
3 工程实例分析
为了验证主成分分析和改进Bayes判别模型的准确率和泛化能力,本文选取国内隧道、国内矿山和国内外矿山隧道3个领域的岩爆实例进行验证。
3.1 大相领隧道
选取北京至昆明高速公路中的大相领隧道进行研究。该隧道地处四川盆地,地形陡峭、埋深大、地应力强,具有典型岩爆现象,选取YK55,YK56,YK61等位置的22组岩爆数据进行分析[25]。大相领隧道岩爆原始数据见表5。将表5数据代入式( 8 ),计算每个工程1,2,3,4等级的先验概率,将计算结果代入式( 12 ),计算kj为6.5。
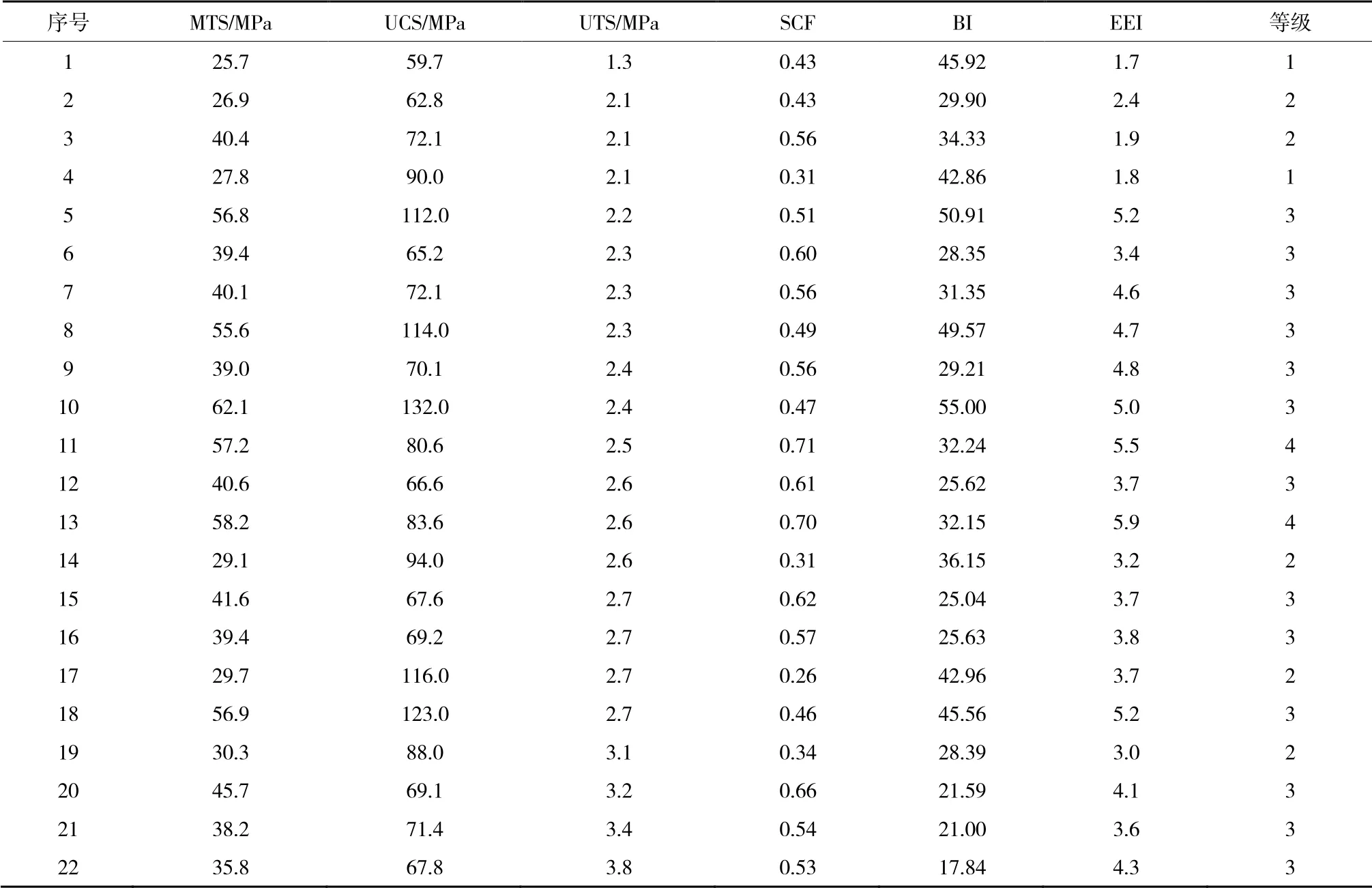
表5 大相领隧道岩爆原始数据Table 5 Original data of rockburst in Daxiangling tunnel
图7为大相领隧道Bayes判别岩爆数据。
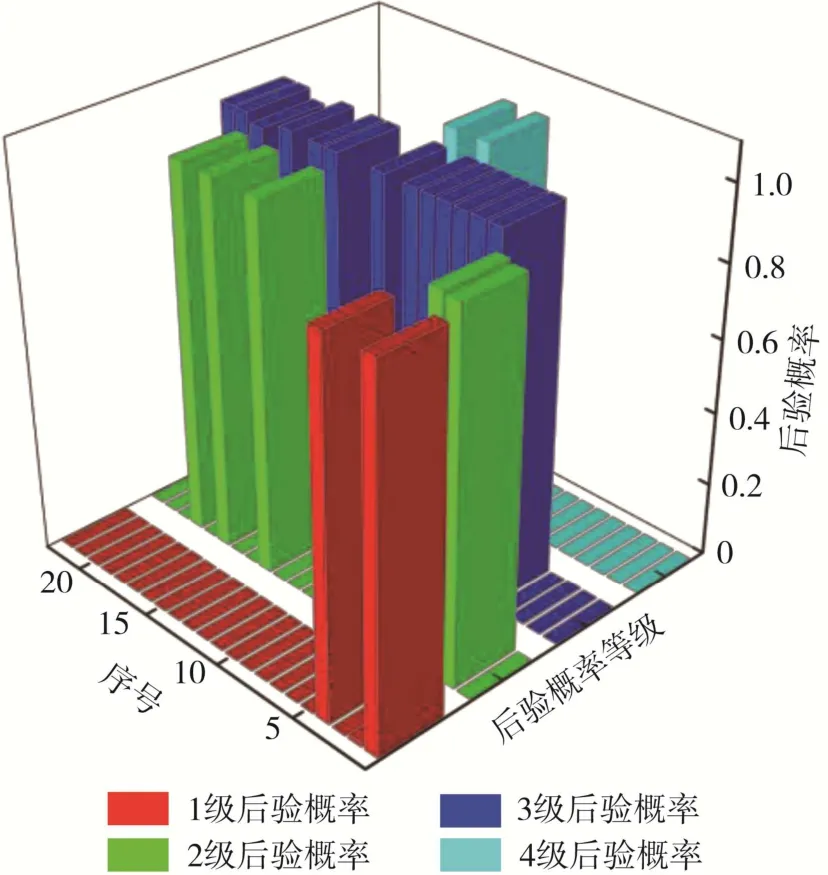
图7 大相领隧道改进Bayes判别岩爆数据Fig. 7 Improved Bayes discrimination of rockburst data in Daxiangling tunnel
根据图7将1,2,3,4等级的后验概率分别代入式( 13 )计算出每组数据ik,得出ki均大于kj,接受判别,岩爆数据的样本均不在分类边界附近,故认为经主成分分析法和Bayes判别的岩爆等级判定是可信的;由图8可知,大相领隧道预测结果与实际结果相符。主成分分析和改进Bayes判别模型应用于隧道中岩爆灾害评价准确率较高。
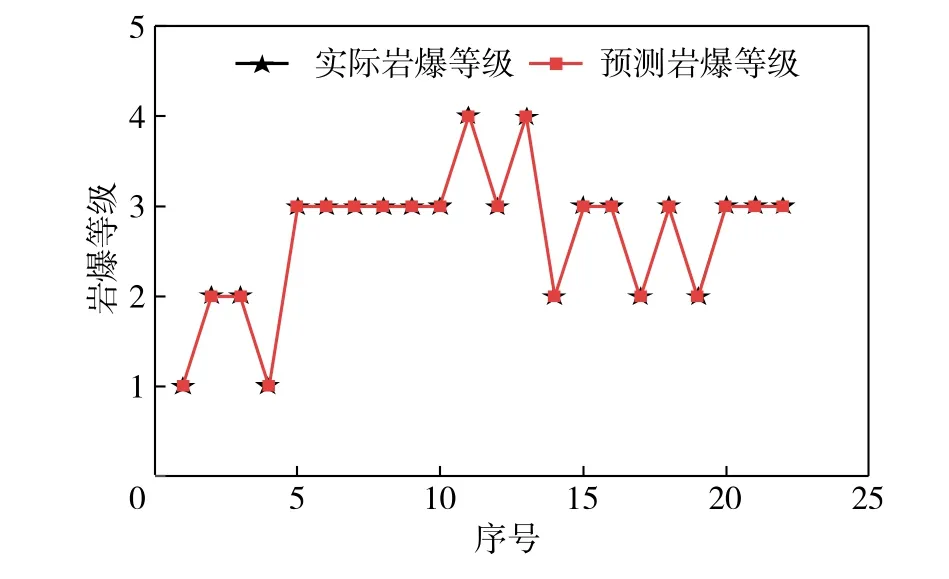
图8 大相领隧道改进Bayes判别岩爆预测等级Fig. 8 Improved Bayes discrimination of rockburst prediction grade in Daxiangling tunnel
3.2 马路坪矿
马路坪矿位于洋水背斜东翼北段,开采深度为600~750 m,随着开采深度和采区地应力增加、围岩表现出明显脆性,部分巷道出现岩爆现象[26]。
表6为马路坪矿岩爆原始数据。将表6数据代入式( 8 ),计算出每个工程1,2,3,4等级的先验概率,将计算结果代入式( 12 ),计算kj为2.5。图9为马路坪矿改进Bayes判别岩爆数据。
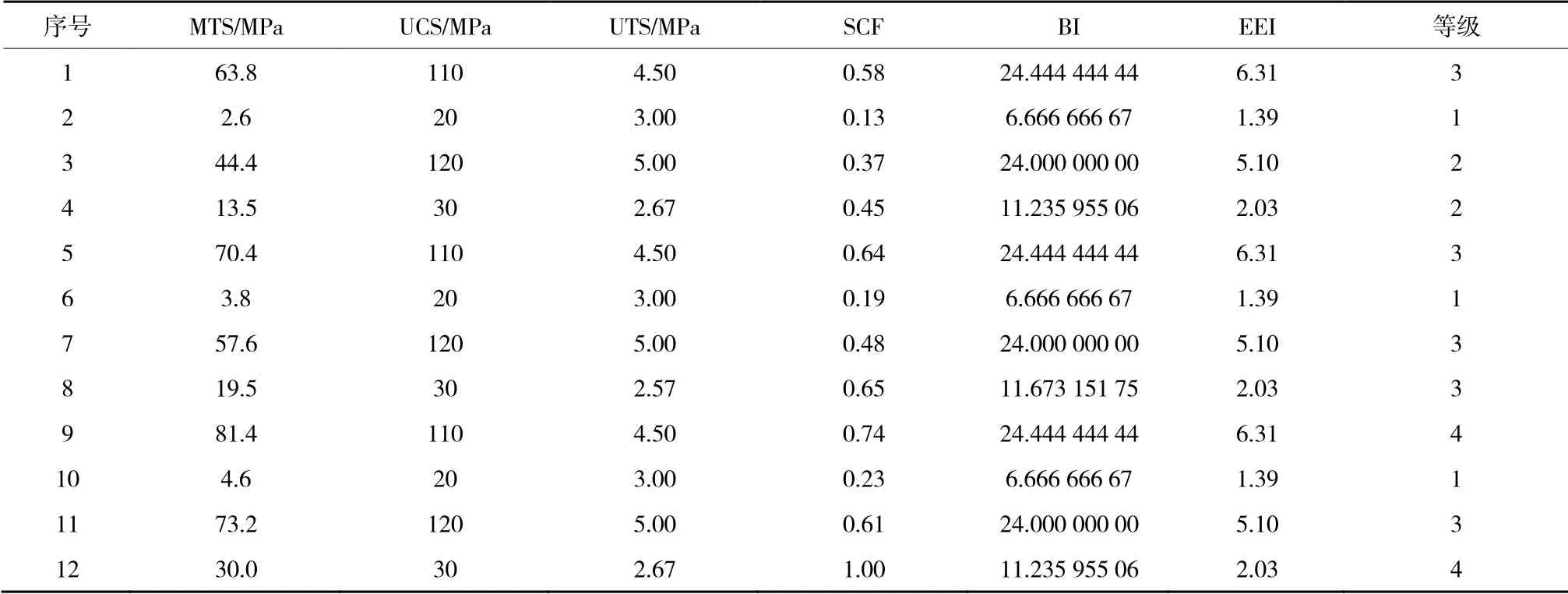
表6 马路坪矿岩爆原始数据Table 6 Original data of rockburst in Maluping Mine
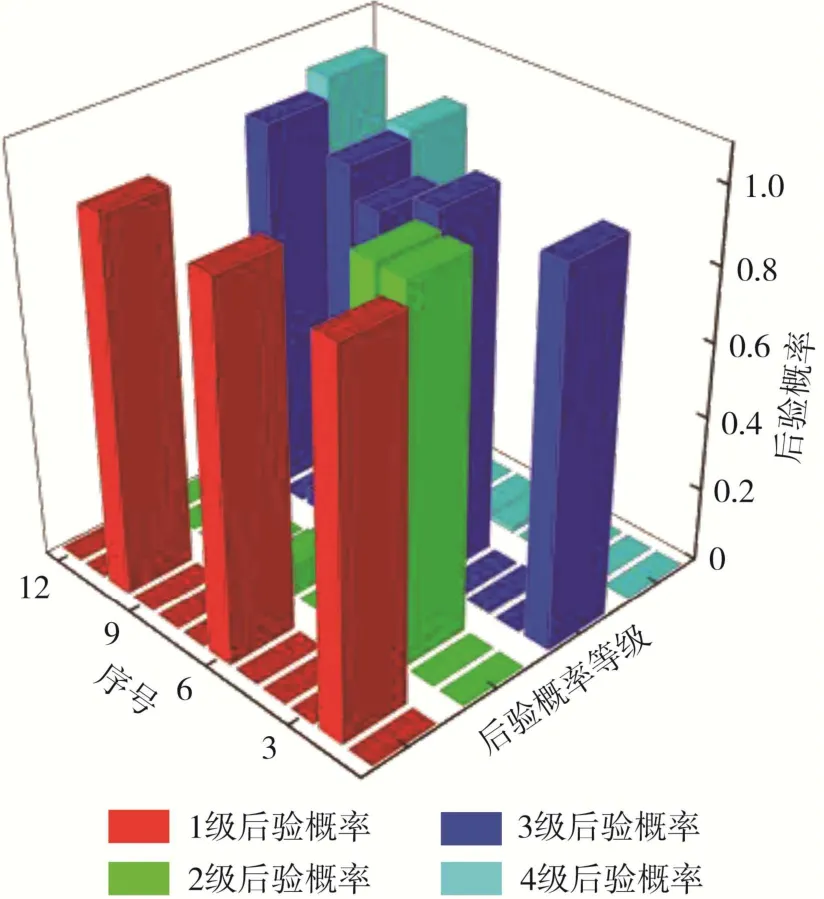
图9 马路坪矿改进Bayes判别岩爆数据Fig. 9 Improved Bayes discrimination of distinguish rockburst data in Maluping Mine
根据图9将1,2,3,4等级的后验概率分别代入式( 13 )计算出每个工程数据ik,得出ik均大于kj,接受判别。认为所有岩爆数据样本在主成分分析法和Bayes判别模型分类中均有效。由图10可知,马路坪矿岩爆预测情况与实际相符,说明主成分分析和改进Bayes判别应用于国内矿山岩爆灾害评价依然有效。
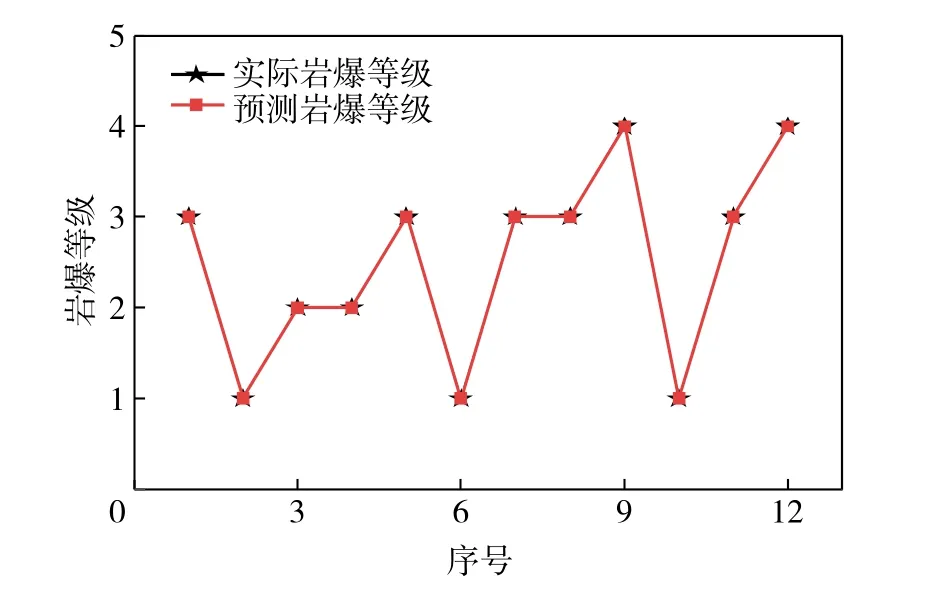
图10 马路坪矿改进Bayes判别岩爆预测等级Fig. 10 Improved Bayes discrimination of rockburst prediction grade in Maluping Mine
3.3 其他国内外矿山隧道
笔者选取其他国内外10个典型的岩爆工程,包括南非金矿、美国CAD-B矿山、前苏联X矿山和瑞士布鲁格水电站地下硐室等,进行岩爆灾害分析[27],岩爆原始数据见表7。将表7数据代入式( 8 )计算每个工程1,2,3,4等级的先验概率,将计算结果代入式( 12 ),计算kj为1.5。图11为国内外典型工程改进Bayes判别岩爆数据,根据图11将1,2,3,4等级的后验概率分别代入式( 13 )计算出每组数据ik。发现其中4k,7k,k10不大于kj,所以拒绝判别,剔出4k,7k,k10三个样本,将剩余样本再次进行Bayes判别运算,判别结果如图12和13所示。
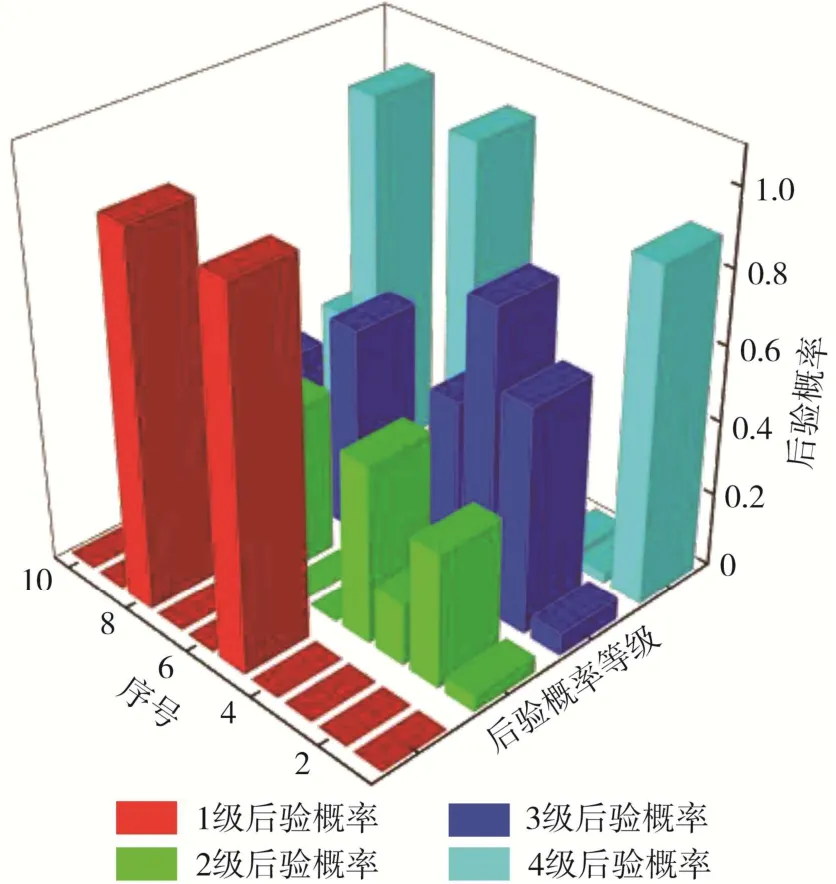
图11 国内外矿山隧道Bayes判别岩爆数据Fig. 11 Bayes discriminant rockburst data of mine tunnels at home and abroad

图12 国内外矿山隧道岩爆预测等级Fig. 12 Prediction grade of rockburst in mine tunnels at home and abroad

表7 国内外矿山隧道岩爆原始数据Table 7 Original data of rockburst at home and abroad
Bayes判别出现2个误判样本( 均为拒绝判别样本 ),阈值修正后预测结果与实际岩爆等级相符,大大提高岩爆预测模型的准确率。
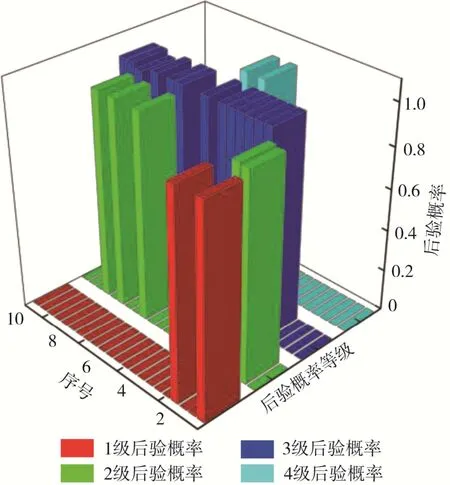
图13 国内外矿山隧道阈值改进Bayes判别岩爆数据Fig. 13 Threshold improved Bayes discrimination of rockburst data of mine tunnels at home and abroad
4 结 论
( 1 ) 提出一种阈值改进Bayes判别的岩爆综合预测模型,模型克服了传统的判别方法受原始数据代表性影响的缺点,通过阈值修正传统模型决策边界分类不确定性的缺点,后验概率小于阈值拒绝判别,提高了岩爆分级的预测精度。该模型方法简单、准确率高,为岩爆分级预测提供借鉴。
( 2 ) 在不同的地质条件下影响岩爆的因素也存在差异,本文中6个影响岩爆的指标中存在参数信息重叠的问题,故采用主成分分析法用3个新指标代替原来指标,且尽可能保留原始变量的信息,为判别分析消除影响,提高Bayes判别的正判率。
( 3 ) 采取综合评判模型对44个样本进行分析,验证主成分分析和阈值改进Bayes判别方法的可行性,并将该方法应用到大相领隧道、马路坪矿和其他国内外相关工程,预测结果与矿山实际情况相符,但也存在部分样本丢失的缺点。丢失样本问题,有待于更深入探索。
