冲击载荷下节理岩体锚固系统剪切动响应分析
2022-10-20赵增辉陈宝森
赵增辉,孙 伟,刘 浩,陈宝森,杨 鹏
( 1. 山东科技大学 能源与矿业工程学院,山东 青岛 266590;2. 山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地,山东 青岛266590 )
节理岩体在地下工程、坝基工程、矿山工程中广泛存在,受开挖扰动、爆破、地震、冲击等动力荷载作用的影响,岩体应力水平突然升高,极易在极短的时间内沿结构面发生大规模剪切滑移,锚杆急剧变形破断,造成锚固支护体系严重失效,从而引发边坡失稳、隧道坍塌、巷道顶板冒落等地质灾害或工程事故[1-5]。节理岩体锚固系统变形破坏程度剧烈,破坏机理复杂,因此,揭示动力荷载下锚固节理岩体的破坏特征对工程灾害防控具有重要意义。
针对加锚节理岩体剪切行为,研究人员运用理论分析、室内试验和数值模拟等手段揭示了加锚节理岩体准静态剪切特性[6-9]。对于动载下剪切行为主要分为2种,一种是将地震、爆破等载荷下动态剪切概念化成不同剪切速率下结构面剪切,如王刚[10]、周子龙[11]、李海波[12]、冯海鹏[13]、刘婷婷[14]等开展了不同剪切速率对软弱结构面、节理面、平直充填节理面剪切强度的影响。另一种则是直接研究冲击、爆破引起的岩体动载响应,如李鹏[15]等建立了爆破载荷下层状节理岩体数值模型,得出爆破应力波在节理岩体中的衰减速度要大于完整岩体的结论;王照刚[16]、胡帅伟[17]、宋千强[18]分析了不同锚固方式、爆破参数、动-静载荷等因素下围岩锚固系统动力响应规律;LI L[19]等通过不同锚杆直径、锚固角和下落高度的落锤冲击双剪试验,得出锚杆弯曲变形受局部剪切力控制,锚杆破断无明显拉伸变形,平均动剪切载荷小于峰值静剪切载荷的结论;吴拥政[20]等进行了加锚岩体侧向冲击试验,结果表明加锚岩体裂缝形态以剪切裂缝和受弯裂缝为主,锚杆强度和韧性能够抑制裂纹的发育。
从现有研究状况看,常法向刚度和常法向应力条件下加锚节理岩体动力冲击承载特性研究不足,冲击作用下加锚节理岩体动载响应、锚杆破断特征和系统静动载剪切异同点仍需深入研究。笔者基于显式动力学分析方法分别对常法向应力和常法向刚度边界条件下加锚节理岩体进行侧向冲击数值计算分析,揭示了冲击载荷作用下加锚节理岩体动响应特征,研究结果可为节理岩体锚固工程防冲设计及改进提供参考。
1 有限元显式动力学问题计算原理
对于动力学问题求解,有限元法的基本思想是将连续的求解区域离散成有限个单元,在一些节点上选择合适的插值函数近似代替场函数,从而将连续域无限自由度问题转变为离散域有限自由度问题。显式动力学算法采用的是中心差分的形式,以每个微小增量步的结果计算下一个增量步结果,无需直接求解切线刚度,算法简单稳健,不存在明显的收敛问题,适用于爆破、冲击、碰撞、复杂屈曲等高度非线性动力学问题[21]。
节点平衡方程为

式中,M为节点质量矩阵;u˙˙为节点加速度;P为施加的外力;I为单元内力。
当增量步开始时刻记为t0,则加速度为
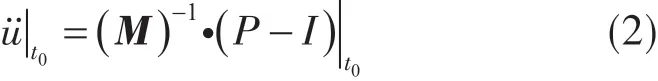
由于显式算法中总是采用集中或对角矩阵,因此求解加速度时无需求解联立方程。任意节点加速度完全可由节点自身质量和作用于节点的合力计算得出,计算成本低。通过对加速度在时间上进行中心差分,同时假定加速度在增量步内为常数,即可求出速度增量,再叠加到前一增量步中点速度,可得到当前增量步中点速度,即

继续对速度在时间上积分,再叠加到增量步开始时位移,可得到增量步结束时位移,即

这样,通过增量步开始时提供的动力学平衡条件,相继计算出加速度、速度和位移,实现在时间层面上的“显式”推进速度和位移。“显式”是指增量步结束时运动状态完全依靠增量步开始时的加速度、速度和位移。
节点增量运动状态计算完成后,根据应变率求得单元应变增量dε,利用本构关系求得增量步结束时应力σ,即,最后集成增量步结束时节点内力
2 加锚节理岩体侧向冲击计算模型
2.1 考虑边界效应的改进数值模型
目前锚固系统动载试验主要采用霍普金森杆动力加载[22]、激振锤[23]、落锤冲击[24]等载荷施加方式,如LI L[19]等针对加锚岩体受冲击载荷作用设计了落锤双剪冲击试验,如图1所示。

图1 落锤双剪冲击试验[19]Fig. 1 Drop hammer double shear impact test[19]
试验系统左右两侧固定,落锤从一定高度位置以自由落体的方式冲击中间岩石,以此分析锚杆动载响应。研究加锚节理岩体动载响应的试验能够以不同方式实现冲击能量的输入,但是无法考虑边界条件的影响。为充分考虑边界约束条件对系统冲击动力学特性的影响,笔者基于ABAQUS设计了改进数值试验方案,图2为三维模型剖面示意图,系统涉及岩石、锚杆、粘结层和冲击体等4种介质,岩石1限制各面法向位移,岩石2限制底面和前后面位移。常法向应力边界条件是岩石1上方施加常法向应力( CNL ),常法向刚度边界条件是岩石1上方施加初始法向应力和弹簧( CNS )。参考LI L[19]等的试验方案,将落锤冲击方式改为冲击体从静止状态以重力加速度做匀加速直线运动,即为横向的落锤冲击加载方式。
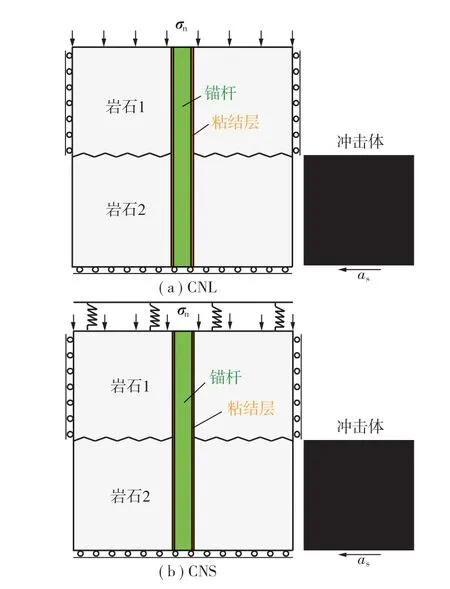
图2 不同边界条件下冲击剪切数值试验方案Fig. 2 Numerical test scheme of impact shear under different boundary conditions
2.2 模型尺寸与参数设置
节理面粗糙度和形貌设置为锯齿长度均为10 mm,取起伏角为10°。岩块尺寸均为150 mm×150 mm×75 mm,粘结层厚度为3 mm,锚杆直径为12 mm。为保证收敛性,岩块、粘结层和锚杆均选用线性减缩积分实体单元,锚杆附近的网格进行局部加密处理。
岩块弹塑性行为采用Mohr-Coulomb准则描述。考虑剪切过程中粘结层因塑性变形积累诱发的刚度劣化,采用混凝土损伤塑性模型( Concrete Damaged Plasticity Model,简称CDP )模拟粘结层的拉伸和压缩破裂行为。引入延性金属损伤模型描述锚杆的颈缩破断。参考相关文献[25-27],岩块、锚杆、粘结层的物理力学参数设置见表1,粘结层的损伤塑性模型参数见表2,锚杆-粘结层-岩石接触力学行为采用“硬”接触摩擦因数表征,各接触面摩擦因数设置见表3。

表1 模型的物理力学参数Table 1 Mechanical parameters of model
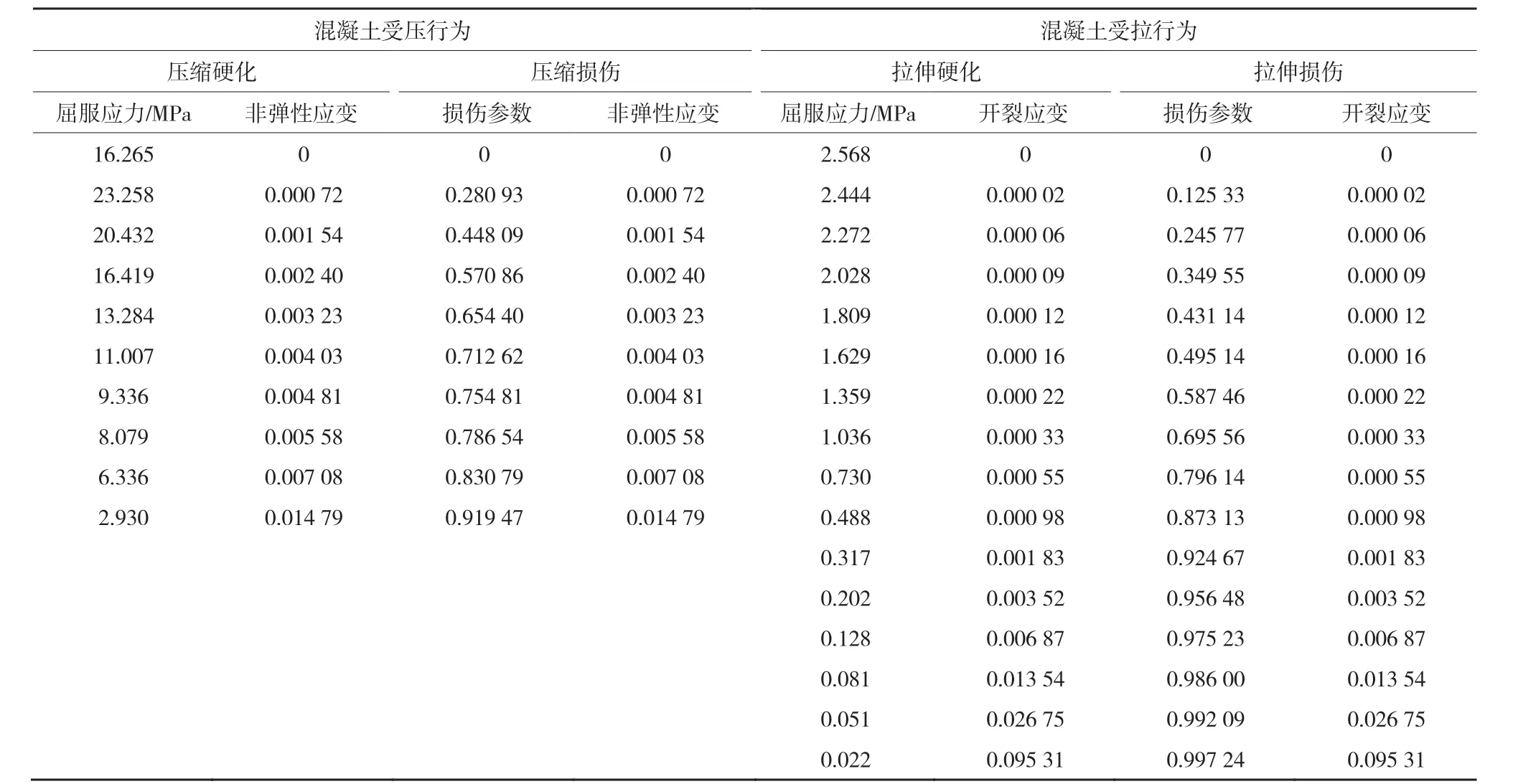
表2 粘结层损伤塑性模型参数Table 2 Damage plastic model parameters of grout

表3 接触面摩擦因数Table 3 Friction factor of contact surfaces
CNL模型法向应力为3 MPa,CNS模型初始法向应力为3 MPa,法向刚度为1 GPa/m。冲击体参数及冲击距离见表4。为输入不同的冲击能量,冲击距离分别设置为50,100,150 mm,水平冲击加速度为9.8 m/s2,则冲击体抵达岩石时对应的速度分别为0.99,1.40,1.71 m/s。冲击体质量约为受冲击岩块的1.5倍,考虑到节理岩体锚固系统尺寸等因素,可认为本文方案符合该节理岩体锚固系统的冲击定义。

表4 冲击体参数及冲击距离Table 4 Parameters of impact body and impact distance
3 加锚节理岩体冲击变形破坏特征
3.1 加锚节理岩体冲击破坏演化过程
CNL边界条件下加锚节理岩体在冲击距离为100 mm时,受冲击作用水平方向应变及破坏特征如图3所示。
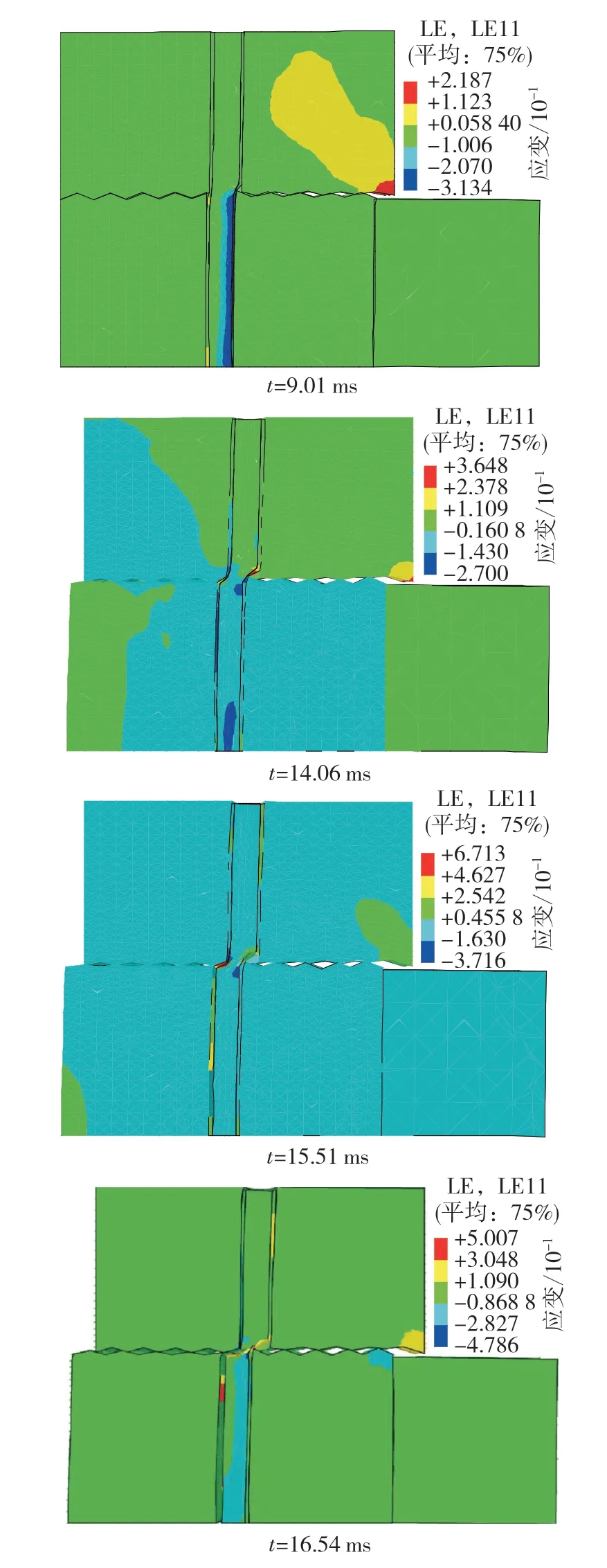
图3 加锚节理岩体受冲击作用水平方向应变及破坏特征Fig. 3 Horizontal strain and failure characteristics of bolted jointed rock mass under impact
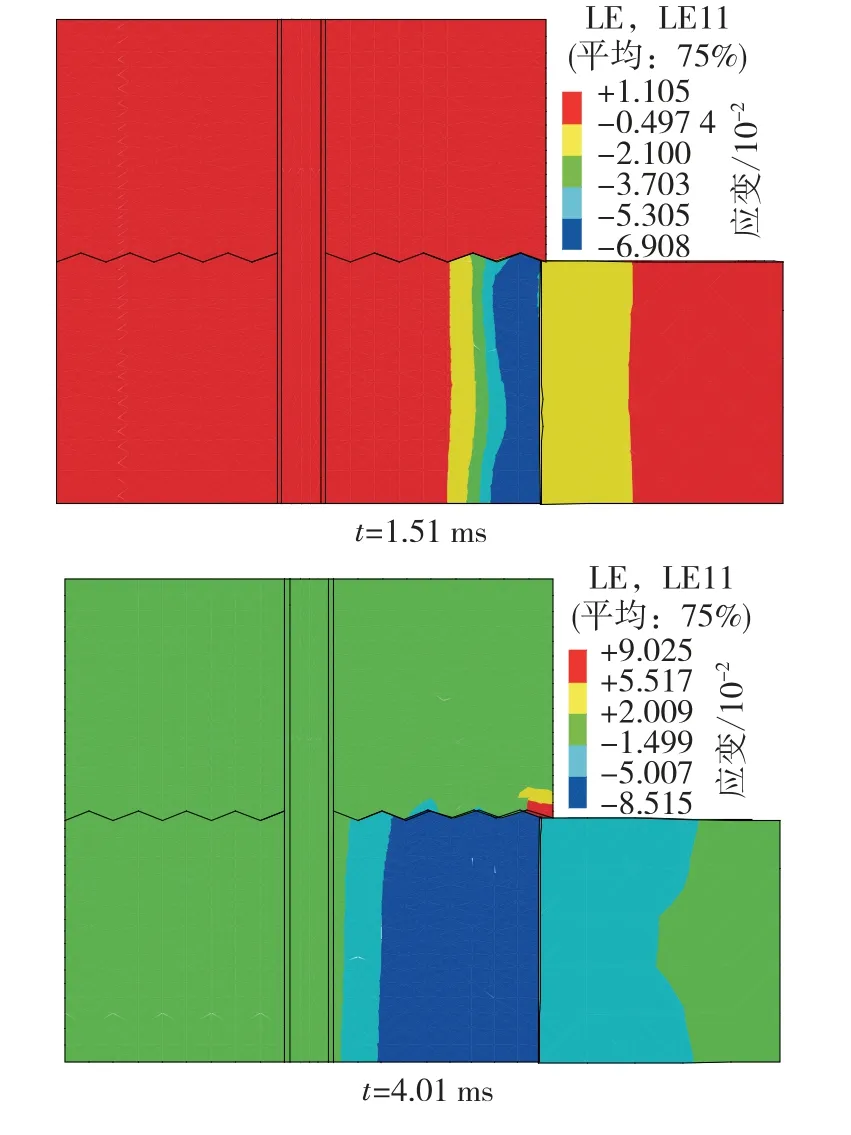
由图3可知,当t=1.51 ms时,冲击体经加速撞击到岩体上,岩石2的右侧迅速出现大致呈条状分布的挤压应变集中区域,随着冲击的进一步进行,挤压应变区向左横向扩展;t=4.01 ms时,由于岩石2的锯齿受挤压向左移动,带动岩石1的锯齿出现拉伸应变,此时锚杆并未产生明显的横向应变,抵抗冲击剪切荷载的主体主要是岩石本身;当t=9.01 ms时,岩石2中的锚杆右侧开始出现条带状挤压应变区,岩石1内部拉伸应变区域从右下角向左上方扩展;当t=14.06 ms时,锚杆应变与岩石2右侧应变在量级上相当,冲击带来的剧烈变形影响完全穿过锚杆下半部分,抵达岩石2左侧,岩石2左侧产生较大的横向挤压变形,向左移动的同时通过锯齿摩擦和剪胀带动岩石1产生向右上方移动趋势,岩石1受左右两侧位移的约束限制,也产生了挤压应变,此时岩石2中粘结层出现局部破碎,锚杆受冲击作用发生了严重的弯曲,积累了大量不可逆塑性变形,损伤加剧,破坏开始出现;当t=15.51 ms时,冲击影响遍布整个节理岩体锚固系统,粘结层单元破碎数量增多,锚杆剪切损伤破坏加剧;当t=16.54 ms时,锚杆已完全破断,锚杆横向抗剪效应失效。CNS边界条件下冲击破坏演化过程类似,不再赘述。
图4为冲击距离100 mm时不同边界条件下节理岩体锚固系统岩石2内部水平速度的演化规律。由图4可知,CNL和CNS边界条件下速度变化的共性是同一时刻右侧速度大,并向左侧快速减小直至为0;随着冲击效应向内部延伸,水平速度呈现向左侧推进的态势,岩石2右侧高速运动区域逐渐增大。2.54 ms和4.55 ms下降曲线斜率大致相同,说明冲击初期岩石横向变形梯度均匀,冲击波动稳定向前推进;6.52 ms时因锚杆横向抗剪约束作用的影响,下降曲线斜率有所减小。在同一时刻相同位置,CNS比CNL边界条件下岩石2的水平速度更小,这是由于CNS边界条件提供了额外的法向应力增量,岩体承受更大的法向应力约束,受冲击影响相对较小。
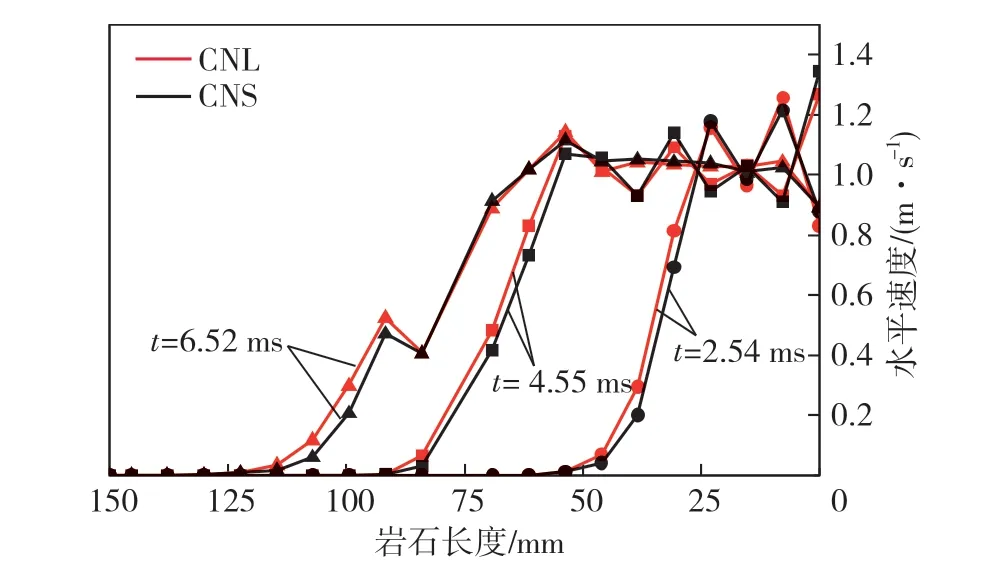
图4 CNL和CNS边界条件下加锚节理岩体内部水平速度演化规律Fig. 4 Evolution of horizontal velocity of bolted jointed rock mass under CNL and CNS boundary conditions
3.2 加锚节理岩体冲击能量演化过程
冲击体从初始速度为0的状态,以恒定的加速度经一定距离撞击到加锚节理岩体上,冲击体自身的动能是节理岩体锚固系统输入的冲击能量。以CNL边界条件为例,阐述冲击过程中冲击体与加锚节理岩体间能量交换及演化机制,CNL边界条件下冲击体和节理岩体锚固系统能量转化如图5所示。
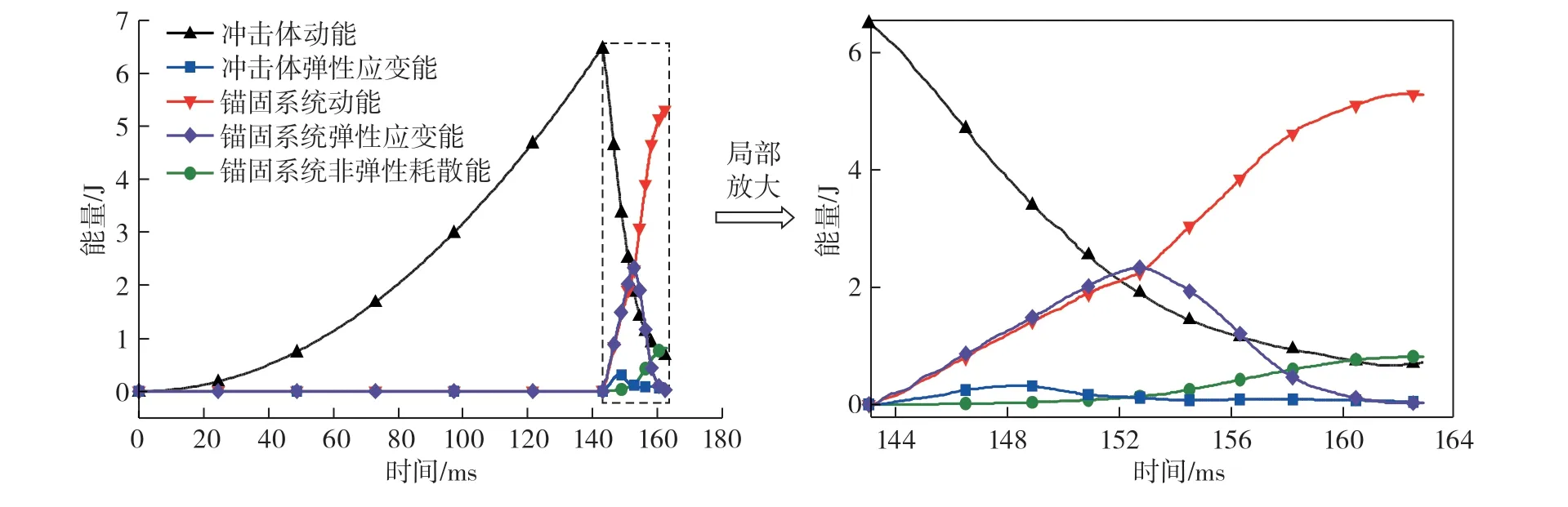
图5 冲击体和加锚节理岩体能量转化Fig. 5 Energy transformation of impact body and bolted jointed rock mass
由图5可知,0~142 ms时,冲击体以9.8 m/s2的均匀加速度作直线运动,其自身动能以抛物线形式积聚,在冲击体和节理岩体锚固系统发生冲击的过程中,冲击体动能逐渐衰减,衰减速度逐渐放缓,冲击体因冲击碰撞其内部出现微小弹性变形而储存少量的弹性应变能,随着冲击的深入,弹性应变能逐步被释放;142~153 ms时,即冲击发生的11 ms内,锚固系统的动能和弹性应变能大致呈线性增加,非弹性耗散能( 主要指塑性变形耗散能量 )基本为0,系统主要以弹性变形为主;153~162 ms时,系统动能仍在增加,储存的弹性应变能开始释放,并逐步转化为耗散能,非弹性耗散能逐渐增加,系统由弹性变形向塑性变形转化。综上可知,输入的冲击动能最终主要转化为冲击体剩余动能和弹性应变能、节理岩体锚固系统动能和弹性应变能、非弹性耗散能,其中以节理岩体锚固系统动能、非弹性耗散能及冲击体剩余动能为主。CNS边界条件下冲击体和节理岩体锚固系统能量交换及演化机制类似,不再赘述。
3.3 锚杆冲击破坏演化规律
锚杆利用自身刚度及强度,为节理岩体提供横向抗剪作用,延缓了冲击导致的变形在岩体的传播速度,锚杆自身则发生严重的弯曲变形甚至破断。冲击距离为100 mm时,锚杆变形破断过程切应变云图和演化规律如图6所示。由图6可知,当t=6.02 ms时,节理面处锚杆右侧出现呈波状分布的切应变集中区;当t=7.57 ms时,切应变集中区外围呈现左窄右宽的喇叭状分布;随着冲击的继续进行,节理面处的锚杆逐渐发生变形,锚杆轴线大致呈Z型,喇叭状分布逐渐收缩直至平行;当t=15.02 ms时,锚杆单元因损伤失效被删除,锚杆出现破碎;当t=16.54 ms时,锚杆完全破断;在6.02~12.04 ms的时间段内,波状分布的切应变集中区逐渐向左扩展,直至贯穿整个锚杆横截面。
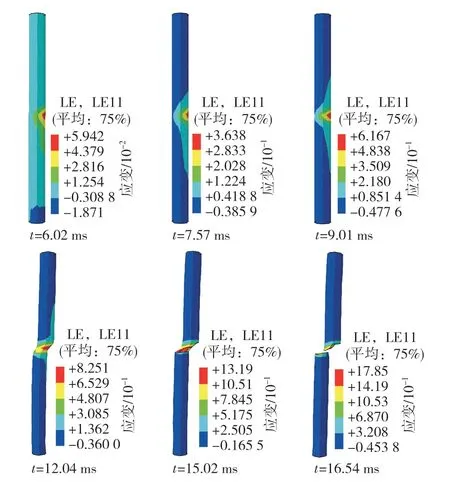
图6 锚杆切应变随冲击时间演化特征Fig. 6 Evolution characteristics of shear strain of bolt with impact time
以锚杆右侧为测线,绘制锚杆右侧切应变随冲击时间的演化曲线,如图7所示。由图7可知,曲线存在最大值,随着冲击时间的延长,切应变最大值逐渐增大,较大切应变区域逐渐收窄,说明锚杆在节理面处受到来自岩石较大的剪切力,剪切力随时间的推移逐渐向节理面处集中,最终产生拉剪破坏。

图7 锚杆右侧切应变随冲击时间的变化曲线Fig. 7 Variation curves of shear strain on the right side of bolt with impact time
图8为不同冲击距离下锚杆破断特征及切应变变化规律。由图8可知,不同冲击距离下锚杆完全破断断面特征大致相同,即下半段锚杆断面平整,上半段锚杆凹凸不平,其断面右侧因单元损伤变形过大被删除,断面左侧单元仍有残留。结合图6进行分析讨论,这主要是由于冲击载荷下锚杆剪切变形破断沿冲击方向进行,不具备静载下剪切变形破断的反对称性。残余切应变主要集中在锚杆断口附近,随着加载距离增大,残余切应变的值逐渐增大。
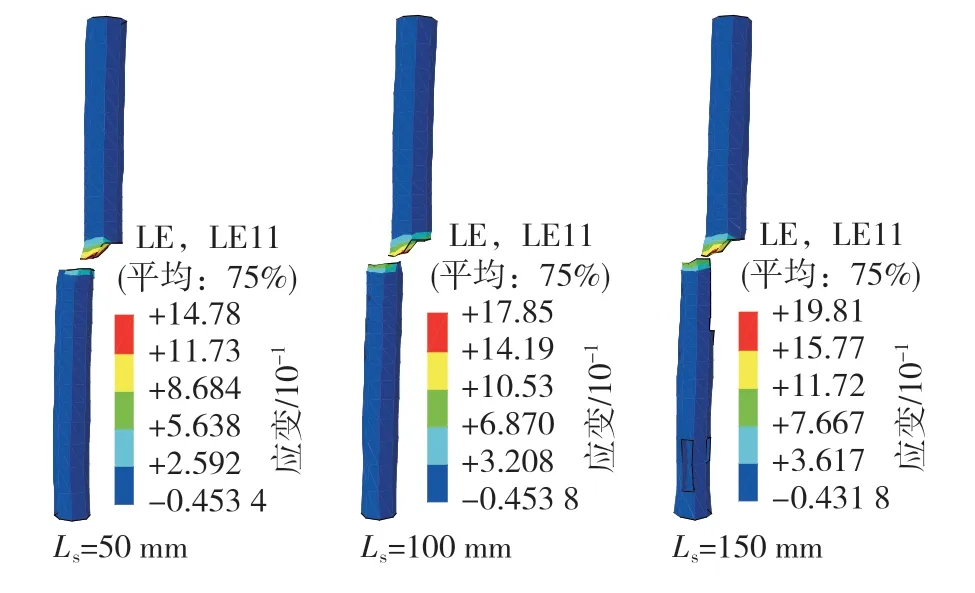
图8 不同冲击距离下锚杆破断特征及切应变变化规律Fig. 8 Breaking characteristics and shear strain variation of bolt under different impact distance
表5为不同冲击距离下锚杆偏转角及破断时间。与静载剪切相比,冲击载荷下锚杆偏转角更小,随着冲击距离增大,偏转角逐渐减小,锚杆开始破断的时间提前,破断所需时间越短,冲击烈度越大。
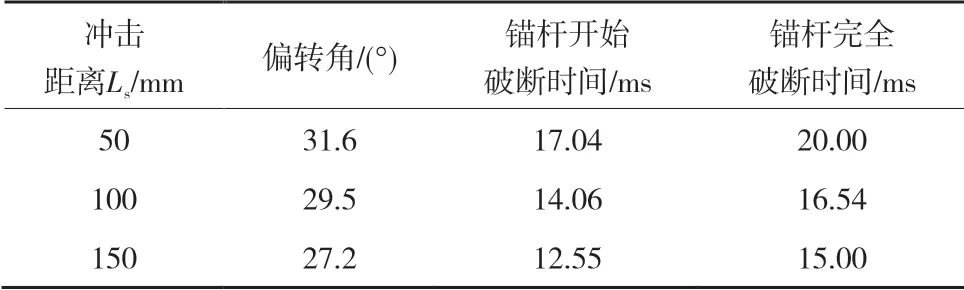
表5 不同冲击距离下锚杆偏转角及破断时间Table 5 Deflection angle and breaking time of bolt under different impact distance
3.4 粘结层冲击累积损伤破坏演化规律
选取节理面位置的粘结层单元,绘制不同冲击距离下其刚度折减系数随冲击时间变化曲线,如图9所示。由图9可知,3种冲击距离下完成刚度折减时间大致相同,同一冲击时刻,冲击距离越大,刚度折减系数越大;增大冲击距离,将对节理岩体锚固系统输入更大的冲击能量,导致剪切变形和节理面附近粘结层损伤加剧,损伤程度更严重。
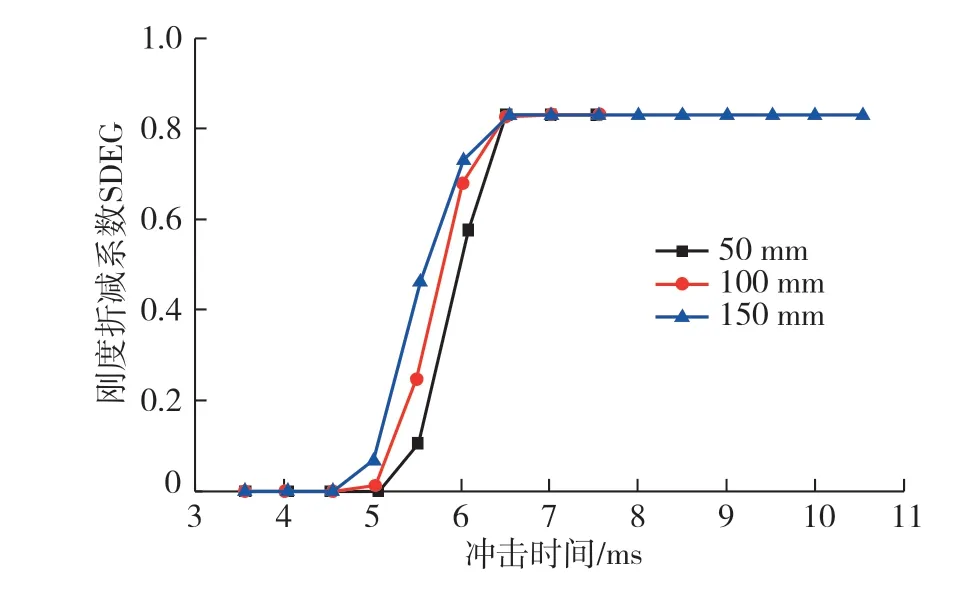
图9 不同冲击距离下粘结层刚度折减系数时程曲线Fig. 9 Time history curves of stiffness reduction factor of bonding layer under different impact distance
4 结 论
( 1 ) 冲击作用下加锚节理岩体变形破坏响应过程与静载作用下有明显不同。冲击初期,岩块是抵抗冲击剪切载荷的主体,岩块沿冲击方向依次出现挤压变形,锚杆起到了减弱岩石挤压变形的作用;随着冲击效应传递,岩块内部也出现大片挤压变形区,锚杆因受冲击作用积累了大量不可逆塑性变形,损伤加剧,最终发生破断,横向抗剪作用失效。
( 2 ) 锚杆剪切动载响应首先在受冲击一侧出现波状分布的切应变集中区;随着冲击的推进,切应变集中区外围分布形态由起初的喇叭状分布逐渐收缩至矩形分布;切应变集中区的内部集中区逐渐收窄,并向另一侧扩展,直至完全贯穿锚杆横截面,切应力逐渐向节理面处集中,最终锚杆发生拉剪破断。
( 3 ) 冲击体的冲击动能最终主要转化为冲击体剩余动能、节理岩体锚固系统动能及非弹性耗散能。冲击距离的增大可为节理岩体锚固系统输入更多冲击能量,锚杆开始破断的时间提前,破断所需时间减少,粘结层损伤加剧,冲击烈度更大。
( 4 ) 冲击初期岩石内部横向变形梯度均匀,冲击波动稳定向前推进,当锚杆开始发挥横向抗剪作用时,波动引起的速度增幅有所下降。同一时刻相同位置的CNS边界条件下受冲击岩石水平速度小于CNL边界条件,主要是因为CNS边界条件岩石承受的法向应力更大,整体性更强,所以受冲击影响相对较小。
