基于局部应变能密度法的缺口多轴疲劳寿命评估

张云平

基于局部应变能密度法的缺口多轴疲劳寿命评估

张云平

（中囯煤炭科工集团上海有限公司，上海 201401）

本文提出了包括实验和数值工作在内的综合分析，阐明了缺口行为对比例多轴疲劳寿命的影响。方法对45钢和45QT钢进行了考虑缺口半径和开口角的多轴疲劳试验，基于平均应变能量密度理论的多轴疲劳分析的分析和计算框架进行了研究，以处理能量梯度。结果显示，大量新的疲劳数据首先通过法向应力和剪应力进行汇总，然后通过凹口尖端周围受控体积中的局部应变能密度重新分析。结论缺口角度对比例载荷下多轴疲劳数据的影响较小，而缺口半径是影响疲劳寿命的主要因素。

比例载荷；多轴疲劳；应变能密度；能量梯度

工程结构部件中因局部设计形成几何不连续情况时有发生，如圆孔、沟槽、倒角、弯折、分叉、焊接余高或角焊缝引起的非连续几何特征等，常称为缺口。该缺口的存在会增加结构局部的应力集中效应，特别在复杂的循环载荷的耦合作用下极易萌生疲劳裂纹，进一步导致裂纹扩展并提前失效。在复杂载荷状态下，局部缺口受多轴应作用产生疲劳失效，成为工程领域研究的主要热点之一。

工程领域中针对缺口的研究多使用名义应力法[1-2]或局部应力应变法[3-4]，但由于缺口尖端附近存在应力集中，缺口效应能引起疲劳寿命的严重下降。通常，处理缺口应力集中的一种基本方法是引入Neuber的应力平均概念作为疲劳行为的局部特征参数。同时，一些先进的疲劳设计概念，如临界距离理论（TCD）[5-6]、应变能密度方法[7-8]用于说明缺口行为并评估包括焊接接头在内的缺口试样的疲劳寿命。这些方法的有效性已通过大量不同载荷条件下的疲劳数据得到验证[9]。另一方面，试样的疲劳寿命取决于缺口敏感性，而缺口敏感性与材料特性有关。尽管EI Haddad参数[10]或Kitagawa和Takahashi的图[11]以及其他缺陷评估准则[12]可以有效地将临界距离确定为固有缺陷（如小裂纹、裂纹和裂纹状缺口）并基于LEFM理论描述短裂纹和长裂纹之间的过渡行为，考虑材料特性与不同锐度 U 和 V 型缺口与多轴疲劳寿命之间关系的文献是有限的。

最近，国内外学者在前人理论基础上结合缺口固有特征提出了新的缺口件多轴疲劳寿命预测方法。芬兰阿尔托大学Gallo研究员不同应力集中程度的316L不锈钢缺口圆棒试件进行了多轴疲劳试验后确定疲劳裂纹由缺口尖端萌生并沿径向扩展，进而基于口尖端附近的应变梯度和最大有效应变作为损伤参量的主要特征，提出了基于缺口应变的寿命预测模型[13]。电子科技大学廖鼎等人将临界距离和应力梯度定义为与疲劳寿命相关的损伤参数从而评估低周多轴疲劳缺口效应[14-15]。与该方法相似的是，Luo等[16]针对薄壁开孔构件将临界面法与临界距离法结合对拉扭多轴疲劳行为展开研究。钟波等[17]提出了等效应力梯度因子解释对缺口效应引起的应力梯度，并应用新的考虑应力梯度影响的多轴缺口件疲劳寿命预测方法。另一方面，部分学者从局部体积法着手确定剪应力随距缺口根部变化的有效损伤距离，进而对多轴疲劳寿命进行有效的预测[18]。刘等[19]扩展了Susmel和Taylor的TCD理论来评估多轴性对缺口疲劳寿命的影响。此外，将缺口根部附近特定损伤区域通过应变能密度进行表征，将不同载荷下的应变能密度值进行叠加获得有效的缺口应变能进行缺口试件的寿命曲线预测缺口件的多轴疲劳寿命[20-22]。应用理论成功综合了严重缺口试样在不同载荷情况下的疲劳寿命表明，当失效发生时，特定控制体积上的应变能密度平均值达到临界值c。

目前，缺口试件多集中在航空航天领域的高温缺口构件展开研究，随着增材制造的技术发展，增材制造件在航空航天的使用进行更多的探索[23-25]，增材制造件的特点随着构件的尺寸变化会产生不同疲劳失效行为。对于结合特定载荷的工程应用，缺口半径变化不定，不同几何形状的缺口形貌下其多轴疲劳行为的评估仍鲜有报道。

文中研究淬火-回火(QT)状态下45钢缺口试样的多轴疲劳强度，在不同拉伸和扭转载荷下测试了不同缺口半径和开口角度试样。轴对称 V 型缺口试样的几何形状具有2个不同的恒定缺口尖端半径（0.2、1 mm）和2个V型缺口开口角度60°和90°。此外，在多轴加载下，缺口试样的半圆半径设置为4.5 mm，并采用平均应变能密度法来评估缺口构件的多轴疲劳寿命。

1 多轴疲劳试验

根据机械设计中的静力准则，首先进行静拉伸试验以确定这些材料的屈服应力。与静态和疲劳载荷相关的材料特性列在表1中，来自实验和参考文献[26]。关于缺口疲劳试样，所有试样在测试前均已抛光，以消除表面划痕或机加工痕迹的影响。采用250KN- MTS809双轴电液伺服试验系统在室温下进行力控多轴疲劳试验。试验设备和缺口试样的方案如图1所示。频率允许在5～10 Hz的范围内，这取决于槽口几何形状和负载水平。这些测试输入值和结果总结见表2—3。其中等效应力计算式见式（1）。

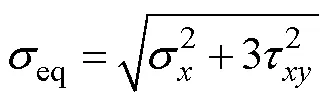
表1 静态和疲劳条件下的材料特性

Tab.1 Material properties under static and fatigue conditions

考虑到2个双轴度比（λ=a/a，λ为1和1.73），在多轴比例拉伸扭转载荷下对具有不同几何结构的试样进行了测试。图2显示了由45钢和45QT钢制成的不同V型缺口试样在比例多轴疲劳载荷下的疲劳数据。可见，缺口半径对2种材料的疲劳寿命都有显着影响。尤其是对于45 QT钢的缺口试样，这种影响可以更明显地表现出来。随着缺口半径的增加，试样的应力集中减小。比较锋利和钝的V型缺口试样的疲劳强度值，缺口半径对疲劳强度影响较大，而疲劳曲线的斜率受应力双轴比的影响。45 QT钢的多轴疲劳结果表明，在相同载荷水平下，其疲劳寿命比45钢更长。

2 分析背景

为了通过合适的局部疲劳特性参数准确评估考虑缺口半径差异的疲劳寿命，控制体积上的线弹性计算用于分析缺口行为并总结实验数据。不同缺口情况下的局部体积如图3所示。最后，可以根据式（2）计算SED。

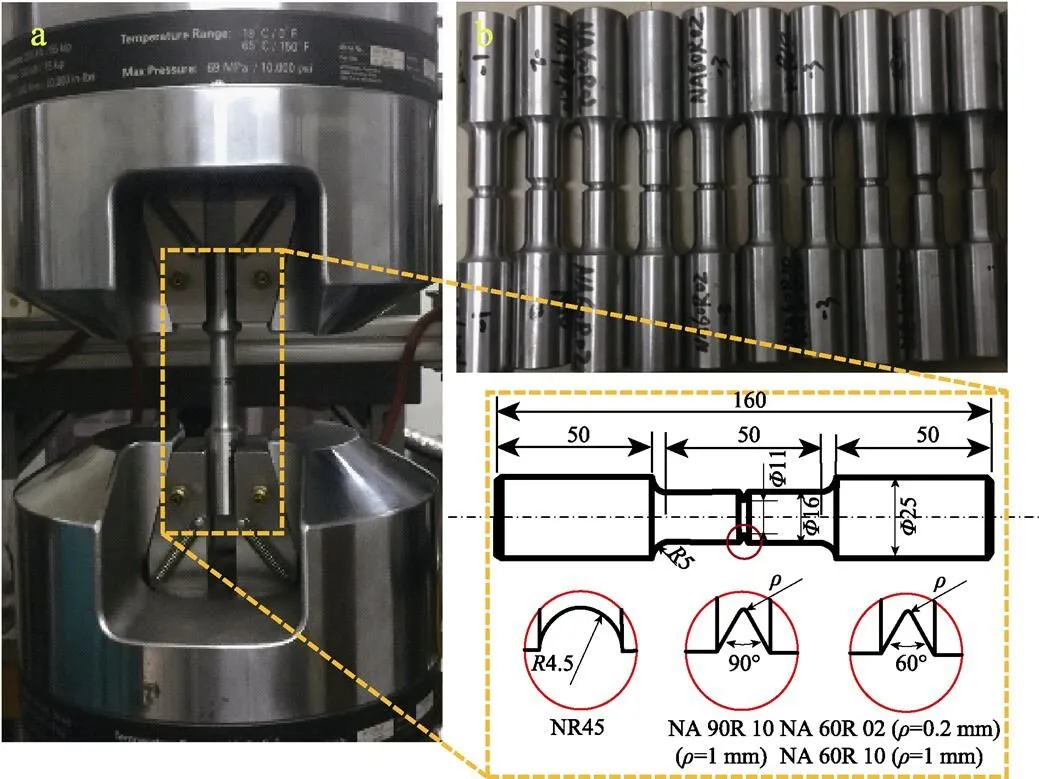
图1 多轴疲劳试验方案及缺口试样

表2 45钢比例载荷多轴疲劳试验结果

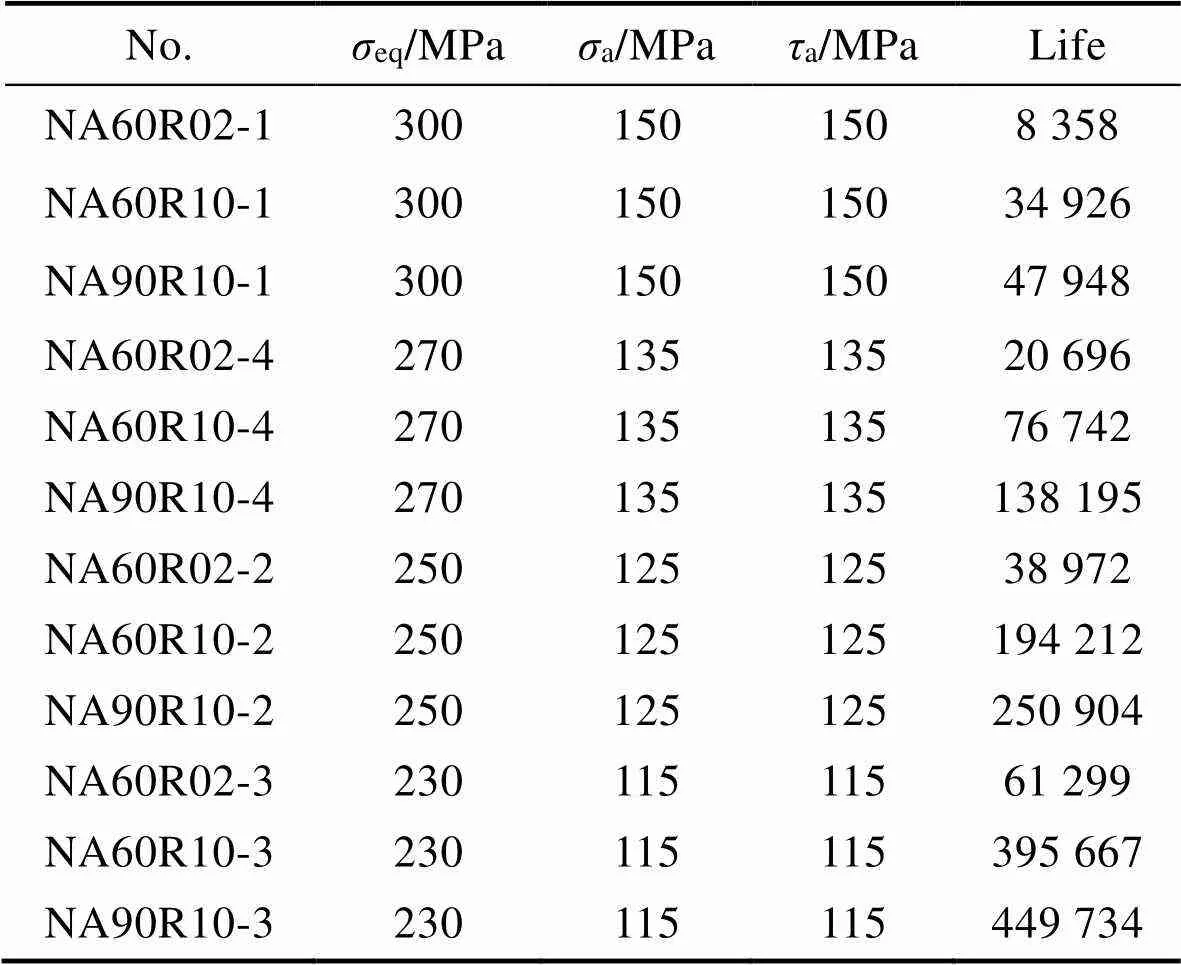
Tab.2 Multiaxial proportional fatigue tests results of 45 steel

表3 45QT钢比例多轴疲劳试验结果

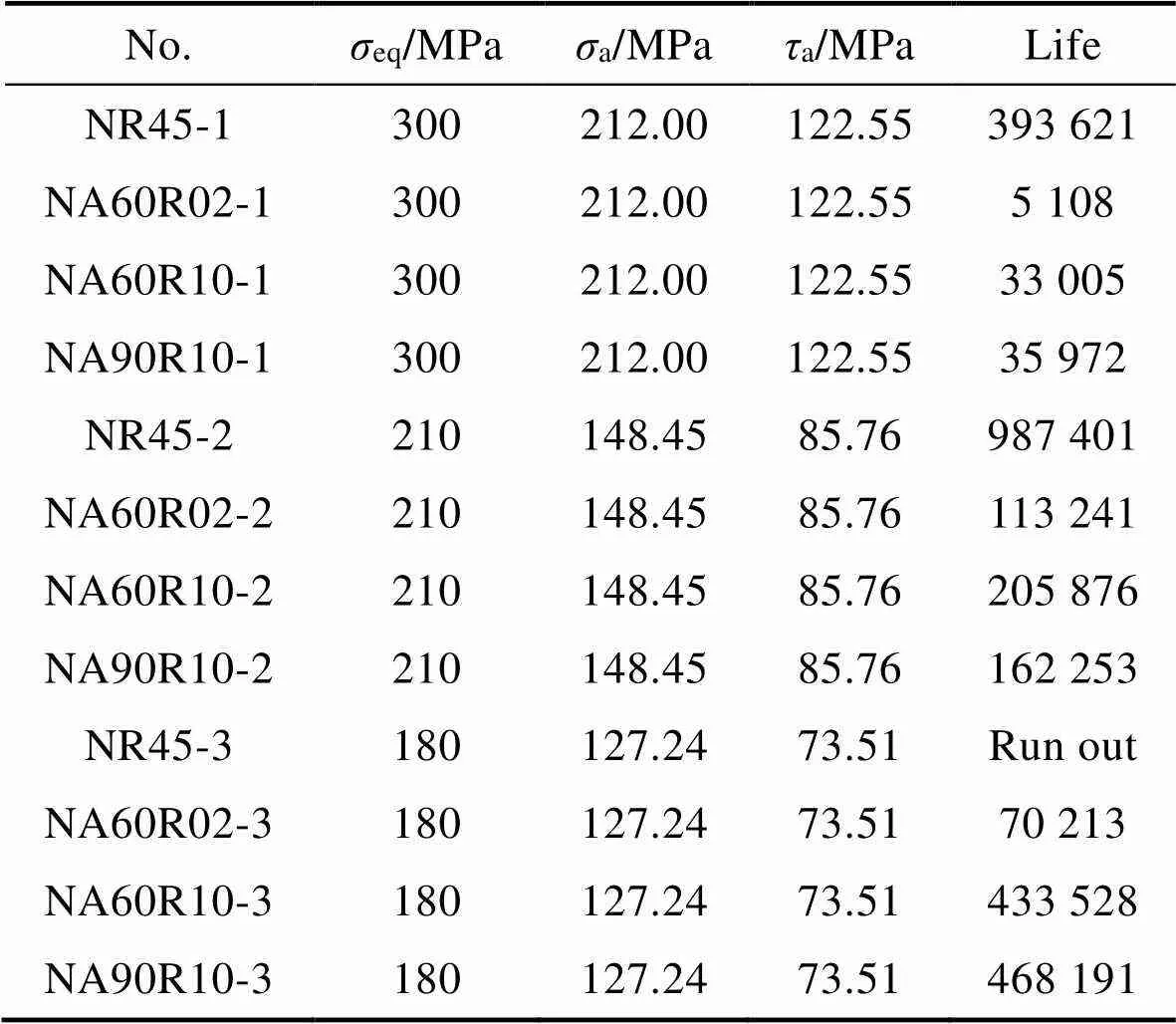
Tab.2 Multiaxial proportional fatigue tests results of 45QT steel

图2 钝性 V 型缺口试样在多轴比例加载下的疲劳数据

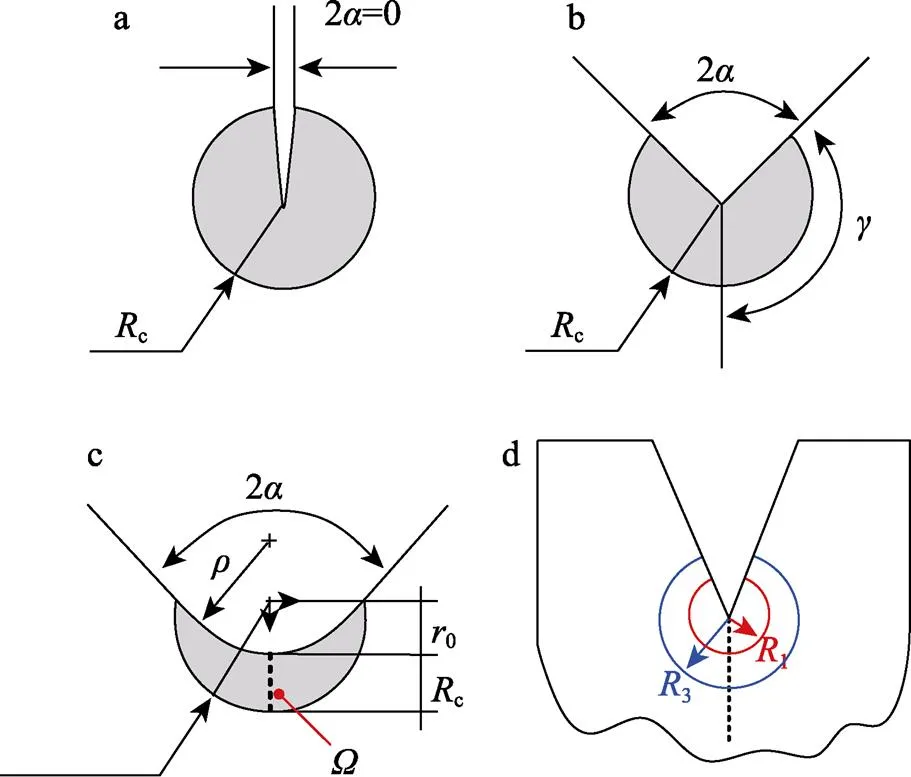
图3 尖锐V型缺口（a）、裂纹（b）和钝V型缺口（c）的控制体积，模式I和模式III的半径（d）

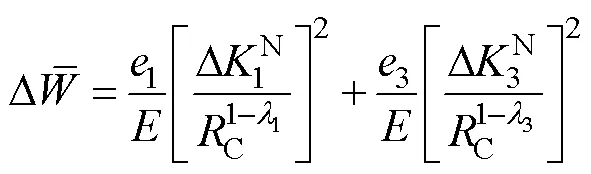
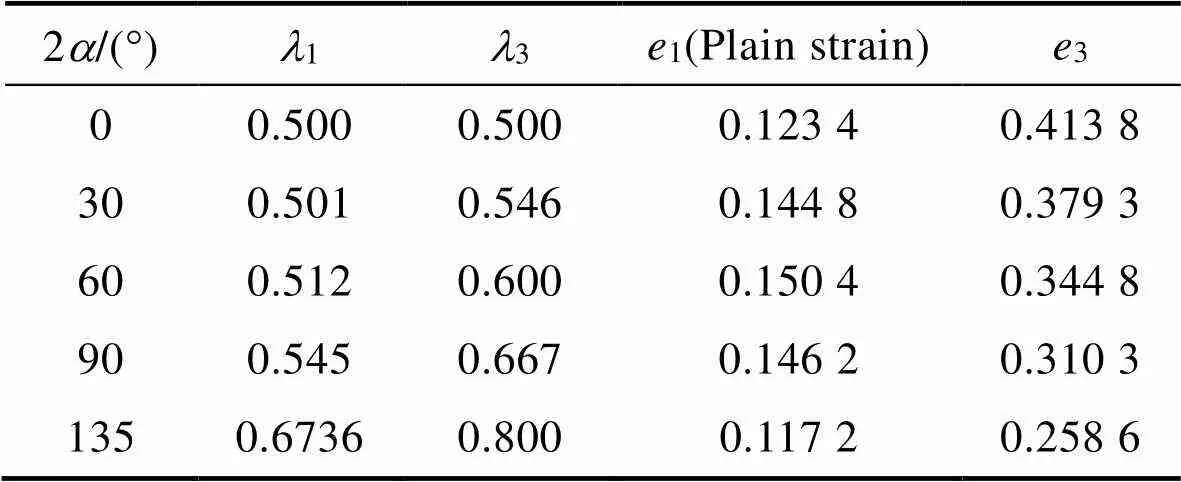
表4 缺口应力分布参数[27]

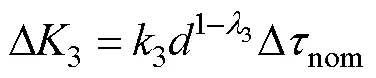
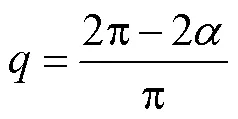
因此，区域的控制体积可以由上述方程计算。此外，可以使用这些方程来计算局部值，并说明尖锐缺口和钝缺口试样之间的疲劳寿命差异。

另一方面，为了说明应力比对疲劳数据的影响，将该参数加入到等式（2）中，并通过大量实验数据进行验证。其和之间的详细关系由等式（8）和等式（9）[29-30]表示。

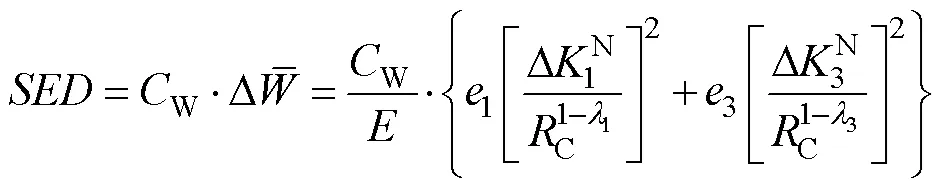
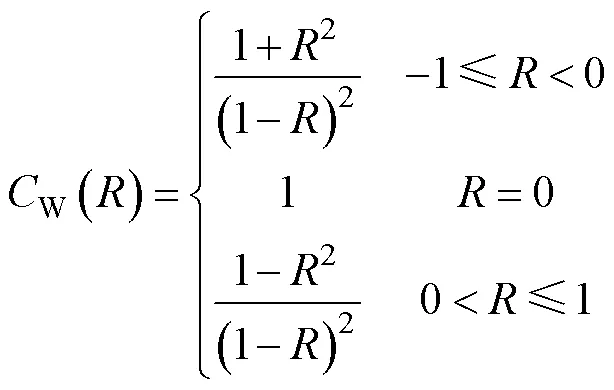
考虑应力比的多轴疲劳数据的所有结果都可以通过上述方程进行总结。这些疲劳数据主要取决于载荷比和双轴度比以及缺口几何形状[31]。计算结果将在下一节中介绍。

3 结果

如图4所示，沿缺口平分线绘制了两个缺口张角下模态I的局部归一化法向应力场和模态III的归一化剪应力场。很明显，奇异项控制局部法向和剪应力分布，最远可达约1 mm的距离。然而，它也证明了2个缺口开口角度（60°和90°）的应力分量分布之间的细微差别。以上2种材料的实验数据验证了缺口张角对多轴疲劳寿命的影响很小。

无缺口和V缺口试样在拉伸和扭转载荷下的值取决于应力强度因子和与材料特性相关的半径值。可以独立获得I型和III型失效的控制体积临界半径，可用于多轴疲劳评估。图5显示了缺口试样的有限元模型。考虑几何对称性，建立了缺口试样的半模型。轴对称应力下的单元类型（CGAX4R）由商业软件ABAQUS选择。

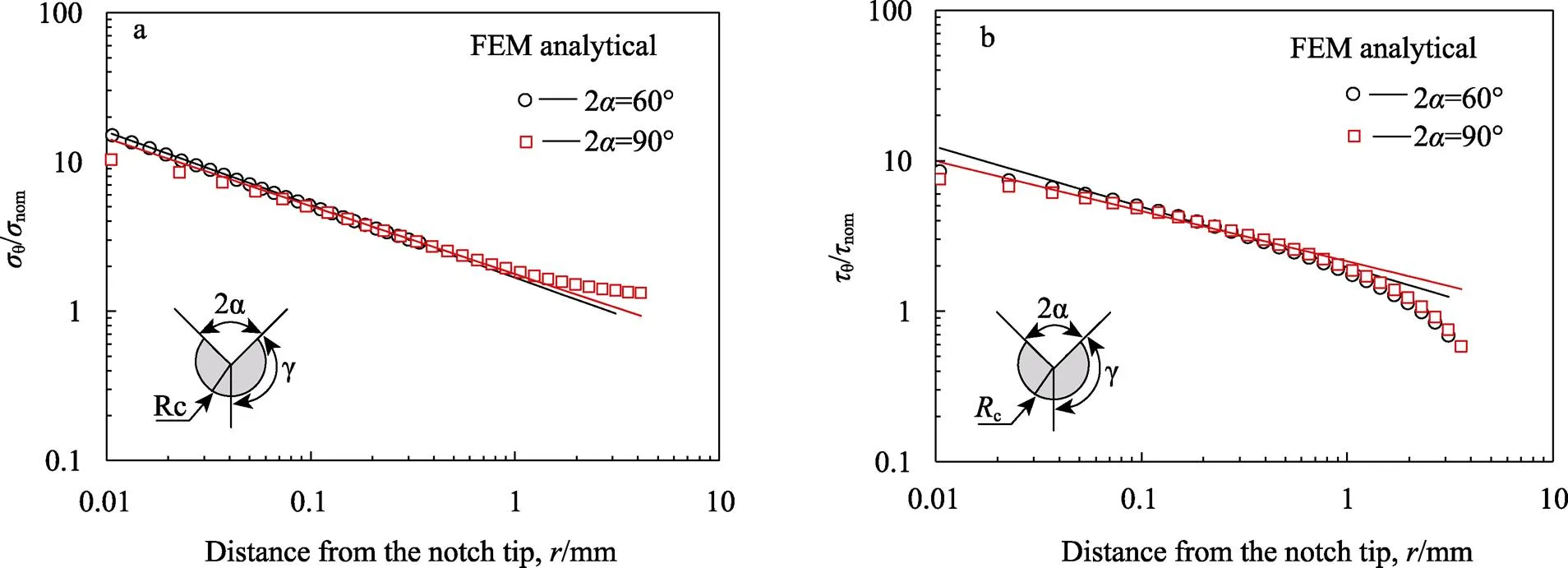
图4 沿缺口平分线的局部法向和剪应力场（I型和III型加载）.

关于在拉伸和扭转载荷条件下的不同配置，分析凹槽尖端周围的梯度以量化能量梯度分布并获得多轴结果。此外，不同缺口半径下的比例多轴疲劳数据由数值值合成。分别在100 MPa张力和扭转载荷下具有不同缺口半径的平均结果也总结在图5中。考虑到理论局部控制体积，张力和扭转值随着凹口半径从0.2 mm增加到1 mm而减小。从图6a—b中可以看出，控制体积中凹口尖端周围的分布随着距凹口尖端距离的增加而减小。与凹槽尖端的峰值值相比，局部控制体积中的平均可以有效地降低梯度。因此，可以通过处理陷波能量梯度来合成具有不同陷波半径的平均。最后，所有疲劳数据都根据图6c—d中所有缺口疲劳数据的进行了总结。从不同缺口半径的疲劳数据对比，使用45和45QT钢的平均值的统一能力可以在关于比例多轴加载的相对较窄的散射带中轻松证明。45和45QT钢的窄带验证了不同缺口试样的普遍适用性。对于45钢和45QT钢，钝缺口试样的散射指数w分别为1.41和3.2。应进一步研究其他多轴疲劳载荷情况，以说明理论疲劳数据的缺口行为。

图5 分别在100 MPa拉伸和扭转载荷下缺口控制体积的平均SED

图6 拉伸载荷（a）和扭转载荷（b）下的SED梯度，基于SED值的45钢（c）和45QT钢（d）缺口试样疲劳结果

4 结论

针对45和45QT钢V形缺口试样，对多轴加载下的缺口能量分布进行数值分析，并获得准确的数据。最后，对缺口试样进行多轴疲劳寿命评估。根据结果分布，结果表明缺口角度对疲劳数据的影响很小，而缺口半径是影响疲劳数据变化的主要因素。基于局部的确定对比例与非比例多轴加载下不同缺口半径的疲劳寿命进行预测，其准确性更高。然而，由于考虑到应力比和其他多轴情况的影响，疲劳数据有限，例如非比例多轴载荷下，其多轴疲劳失效行为以及与疲劳特性参数之间的关系仍需进一步系统研究。

[1] GOUGH H J, POLLARD H V. Properties of some Materials for Cast Crankshafts, with Special Reference to Combined Stresses[J]. Proceedings of the Institution of Automobile Engineers, 1936, 31(1): 821-893.

[2] 吴文涛, 王英玉. 一种新的多轴缺口疲劳寿命预测方法[J]. 飞机设计, 2015, 35(4): 41-46, 60.

WU Wen-tao, WANG Ying-yu. A New Method for Multi-Axis Notch Fatigue Life Prediction[J]. Aircraft Design, 2015, 35(4): 41-46, 60.

[3] MOLSKI K, GLINKA G. A Method of Elastic-Plastic Stress and Strain Calculation at a Notch Root[J]. Materials Science and Engineering, 1981, 50(1): 93-100.

[4] 邱宝象, 王效贵, 高增梁. 基于A-F类循环塑性理论的多轴局部应力应变法[J]. 机械强度, 2011, 33(4): 590-596.

QIU Bao-xiang, WANG Xiao-gui, GAO Zeng-liang. Multiaxial Local stress-Strain Approach Based on a-F Type Cyclic Plasticity Theory[J]. Journal of Mechanical Strength, 2011, 33(4): 590-596.

[5] SUSMEL L, TAYLOR D. A Novel Formulation of the Theory of Critical Distances to Estimate Lifetime of Notched Components in the Medium-Cycle Fatigue Regime[J]. Fatigue & Fracture of Engineering Materials and Structures, 2007, 30(7): 567-581.

[6] SUSMEL L. The Theory of Critical Distances: A Review of Its Applications in Fatigue[J]. Engineering Fracture Mechanics, 2008, 75(7): 1706-1724.

[7] BERTO F, CAMPAGNOLO A, LAZZARIN P. Fatigue Strength of Severely Notched Specimens Made of Ti-6Al-4V under Multiaxial Loading[J]. Fatigue & Fracture of Engineering Materials & Structures, 2015, 38(5): 503-517.

[8] LAZZARIN P, BERTO F, ZAPPALORTO M. Rapid Calculations of Notch Stress Intensity Factors Based on Averaged Strain Energy Density from Coarse Meshes: Theoretical Bases and Applications[J]. International Journal of Fatigue, 2010, 32(10): 1559-1567.

[9] BERTO F, CAMPAGNOLO A, CHEBAT F, et al. Fatigue Strength of Steel Rollers with Failure Occurring at the Weld Root Based on the Local Strain Energy Values: Modelling and Fatigue Assessment[J]. International Journal of Fatigue, 2016, 82: 643-657.

[10] EL HADDAD M H, TOPPER T H, SMITH K N. Prediction of Non Propagating Cracks[J]. Engineering Fracture Mechanics, 1979, 11(3): 573-584.

[11] PESSARD E, BELLETT D, MOREL F, et al. A Mechanistic Approach to the Kitagawa-Takahashi Diagram Using a Multiaxial Probabilistic Framework[J]. Engineering Fracture Mechanics, 2013, 109: 89-104.

[12] ATZORI B, LAZZARIN P, MENEGHETTI G. Fracture Mechanics and Notch Sensitivity[J]. ≫ Fracture of Engineering Materials and Structures, 2003, 26(3): 257-267.

[13] GALLO P, BRESSAN S, MORISHITA T, et al. Analysis of Multiaxial Low Cycle Fatigue of Notched Specimens for Type 316L Stainless Steel under Non-Proportional Loading[J]. Theoretical and Applied Fracture Mechanics, 2017, 89: 79-89.

[14] LIAO Ding, ZHU Shun-peng, QIAN Gui-an. Multiaxial Fatigue Analysis of Notched Components Using Combined Critical Plane and Critical Distance Approach[J]. International Journal of Mechanical Sciences, 2019, 160: 38-50.

[15] LIAO Ding, ZHU Shun-peng, CORREIA J A F O, et al. Computational Framework for Multiaxial Fatigue Life Prediction of Compressor Discs Considering Notch Effects[J]. Engineering Fracture Mechanics, 2018, 202: 423-435.

[16] LUO Peng, YAO Wei-xing, LI Piao. A Notch Critical Plane Approach of Multiaxial Fatigue Life Prediction for Metallic Notched Specimens[J]. Fatigue & Fracture of Engineering Materials & Structures, 2018: ffe.12956.

[17] 钟波, 王延荣, 魏大盛. 考虑应力梯度影响的多轴缺口疲劳寿命预测[J]. 航空动力学报, 2018, 33(11): 2602-2610.

ZHONG Bo, WANG Yan-rong, WEI Da-sheng. Multiaxial Notch Fatigue Life Prediction Based on Stress Gradient Effect[J]. Journal of Aerospace Power, 2018, 33(11): 2602-2610.

[18] 谭晶莹, 李江华, 孙然, 等. 基于体积法的缺口件多轴疲劳寿命预测[J]. 应用力学学报, 2016, 33(4): 726-730, 746.

TAN Jing-ying, LI Jiang-hua, SUN Ran, et al. Fatigue Life Prediction for Notched Specimen Based on the Volume Approach under Multiaxial Loading[J]. Chinese Journal of Applied Mechanics, 2016, 33(4): 726-730, 746.

[19] LIU Bo-wen, YAN Xiang-qiao. An Extension Research on the Theory of Critical Distances for Multiaxial Notch Fatigue Finite Life Prediction[J]. International Journal of Fatigue, 2018, 117: 217-229.

[20] RAZAVI S M J, PERON M, TORGERSEN J, et al. 40CrMoV13.9Notched Specimens under Multiaxial Fatigue: An Overview of Recent Results[J]. Frattura Ed Integrità Strutturale, 2017, 11(41): 440-446.

[21] BRANCO R, PRATES P A, COSTA J D, et al. New Methodology of Fatigue Life Evaluation for Multiaxially Loaded Notched Components Based on Two Uniaxial Strain-Controlled Tests[J]. International Journal of Fatigue, 2018, 111: 308-320.

[22] MENEGHETTI G, CAMPAGNOLO A, BERTO F, et al. Notched Ti-6Al-4V Titanium Bars under Multiaxial Fatigue: Synthesis of Crack Initiation Life Based on the Averaged Strain Energy Density[J]. Theoretical and Applied Fracture Mechanics, 2018, 96: 509-533.

[23] 陈国庆, 树西, 张秉刚, 等. 国内外电子束熔丝沉积增材制造技术发展现状[J]. 焊接学报, 2018, 39(8): 123-128.

CHEN Guo-qing, SHU Xi, ZHANG Bing-gang, et al. State-of-Arts of Electron Beam Freeform Fabrication Technology[J]. Transactions of the China Welding Institution, 2018, 39(8): 123-128.

[24] 顾冬冬, 张红梅, 陈洪宇, 等. 航空航天高性能金属材料构件激光增材制造[J]. 中国激光, 2020, 47(5): 32-55.

GU Dong-dong, ZHANG Hong-mei, CHEN Hong-yu, et al. Laser Additive Manufacturing of High-Performance Metallic Aerospace Components[J]. Chinese Journal of Lasers, 2020, 47(5): 32-55.

[25] 李权, 王福德, 王国庆, 等. 航空航天轻质金属材料电弧熔丝增材制造技术[J]. 航空制造技术, 2018, 61(3): 74-82.

LI Quan, WANG Fu-de, WANG Guo-qing, et al. Wire and Arc Additive Manufacturing of Lightweight Metal Components in Aeronautics and Astronautics[J]. Aeronautical Manufacturing Technology, 2018, 61(3): 74-82.

[26] CHEN, XU, HUANG. A Critical Plane-Strain Energy Density Criterion for Multiaxial Low-Cycle Fatigue Life under Non-Proportional Loading[J]. Fatigue & Fracture of Engineering Materials & Structures, 1999, 22(8): 679-686.

[27] LAZZARIN P, ZAMBARDI R. A Finite-Volume-Energy Based Approach to Predict the Static and Fatigue Behavior of Components with Sharp V-Shaped Notches[J]. International Journal of Fracture, 2001, 112(3): 275-298.

[28] BERTO F, LAZZARIN P, YATES J R. Multiaxial Fatigue of V-Notched Steel Specimens: A Non-Conv­en­tional Application of the Local Energy Method[J]. Fatig­ue & Fracture of Engineering Materials & Structures, 2011, 34(11): 921-943.

[29] SONG Wei, LIU Xue-song, XU Jie, et al. Fatigue Fracture Assessment of 10CrNi3MoV Welded Load-Carrying Cruciform Joints Considering Mismatch Effect[J]. Fatigue & Fracture of Engineering Materials & Structures, 2021: ffe.13457.

[30] SONG Wei, LIU Xue-song, XU Jie, et al. Multiaxial Low Cycle Fatigue Assessment of Notch Specimens for 10CrNi3MoV Steel and Its Welds[J]. Procedia Structural Integrity, 2020, 28: 200-207.

[31] SONG Wei, SU Lin, XU Jie, et al. Combined Effect of Prestrain History and Strength Mismatch on Crack Tip Constraints in Welded Specimen[J]. Material Design & Processing Communications, 2020, 2(6): 1-9.

Assessment of Notch Multiaxial Fatigue Life Based on Local Strain Energy Density Method

ZHANG Yun-ping

(China Coal Science and Industry Group (Shanghai) Co., Ltd., Shanghai 201401, China)

In this paper, a comprehensive analysis including experimental and numerical work is presented to illustrate the effect of notch behavior on proportional multiaxial fatigue life. Methods multiaxial fatigue tests were carried out on 45 steel and 45QT steel considering notch radius and opening angle. The analytical and computational framework of multiaxial fatigue analysis based on the theory of average strain energy density was studied to deal with energy gradient. A large number of new fatigue data were first summarized by normal stress and shear stress, and then reanalyzed by local strain energy density in the controlled volume around the notch tip. Conclusion the notch angle has little effect on the multiaxial fatigue data under comparative load, and the notch radius is the main factor affecting the fatigue life.

proportional load; multiaxial fatigue; strain energy density; energy gradient

10.3969/j.issn.1674-6457.2022.10.022

TG456.7

A

1674-6457(2022)10-0155-07

2021‒12‒30

天地科技/产学研大渗层高性能重载齿轮关键制造技术及产业化研究（2020-2-TD-CXY001）；常熟市工业攻关长寿命导向滑靴用新材料及关键制备技术的研究（CG202108）；苏州市重点产业技术创新项目采煤机主关件增材制造长寿命耐磨层关键技术及装备研发（SGC20211126）

张云平（1968—），男，高级工程师，主要研究方向为金属结构件加工与成型。