内高压成形合模力对变径管尺寸精度的影响
2022-10-20崔晓磊王祎纯温时宇徐旺成
崔晓磊,王祎纯,温时宇,徐旺成
内高压成形合模力对变径管尺寸精度的影响
崔晓磊a,b,王祎纯b,温时宇b,徐旺成b
(哈尔滨工业大学 a.金属精密热加工国家级重点实验室;b.材料科学与工程学院,哈尔滨 150001)
在内高压成形过程中,合模力加载不合理不仅会导致模具寿命降低,而且容易引起管件截面精度超差,需探究合模力对管件截面尺寸的影响以改善这一缺陷。以低碳钢和铝合金变径管为例,采用内高压成形实验与数值模拟的方法,在两种不同的加载条件下分析合模力对管件截面尺寸精度的影响规律。变径管内高压成形时,模腔上、下侧的等效应力高于左、右侧,模腔顶部的径向位移最小,分型面附近的径向位移最大。模腔在合模力的作用下被压扁,导致卸载内压和合模力后管件截面竖直方向的直径始终小于水平方向,存在一定的不圆度。SAPH440低碳钢和6063铝合金变径管的截面最大不圆度分别为0.27%和0.26%。在内高压成形过程中,合模力对截面精度的影响不可避免,需通过增大模具尺寸或采用可变合模力的加载方式以减小其影响。
内高压成形;变径管;合模力;尺寸精度;不圆度
内高压成形是一种一体化制造变截面薄壁管件的先进成形技术[1-3],因其成形的零件质量好、强度高,且能够实现结构轻量化,所以被广泛应用于航空航天和汽车领域[4-5]。与传统冲焊工艺相比,内高压成形以封闭管坯作为初始坯料,避免了焊接变形对零件精度的影响,因此通常具有较高的形状精度和尺寸精度[6-8]。然而,当管坯在内高压成形过程中受到不合理的应力作用时,也会产生失稳起皱、破裂和精度超差等缺陷[9-12]。
管件的成形精度对后续装配和结构整体性十分重要。因此,对于内高压成形管件精度的控制极其关键。Nakamori等[13]采用高精度内置传感器监控了6063-T5铝合金Y形管的内高压成形过程,结果显示,管件横截面存在一定的不圆度。蔡洋等[14]以内高压成形6063-T4铝合金副车架横梁为研究对象,测得两个典型截面的最大尺寸偏差分别为0.19 mm(0.4%)、0.28 mm(0.49%)。陈名涛等[15]以并列双支管为例,通过分析其内高压成形过程的金属流动规律,发现支管仅靠单边轴向压缩完成补料,支管中心向内偏移,支管形状呈现非对称结构。Vollertsen[16]指出,内高压成形管件的尺寸精度主要受到固有误差、系统误差和随机误差的影响。其中,固有误差主要来自模具加工误差及管件回弹;系统误差主要来自于模具磨损;而随机误差主要来自于管坯壁厚与强度的差异以及工艺参数的不同。
对轿车扭力梁内高压成形后的精度进行研究发现,调节轴向进给能显著改善截面精度。无轴向进给时,截面尺寸最大偏差为2.7%;当轴向进给增加到8%时,尺寸偏差降低到0.5%以内[17]。在弯管内高压成形时,通过改善预弯曲芯轴的条件可将截面不圆度由7.55%降低至1.43%,避免了弯曲件在内高压成形时发生破裂[18]。此外,采用充液压弯管坯进行内高压成形可以获得更好的管件尺寸精度[19]。为进一步提高管件成形精度,提出通过控制内压大小使模具弹性变形量恰好等于管件回弹量,从而使管件的最终尺寸恰好等于设计值[20]。然而,目前的研究主要关注管件截面某一方向的尺寸精度及其调控。实际上,若合模力在内高压成形过程中施加不当,容易导致管件截面不同方向的尺寸精度或形状精度超差[21]。
文中以SAPH440低碳钢和6063铝合金变径管为例,通过内高压成形实验与数值模拟,研究不同合模力下的变径管截面尺寸与不圆度,分析合模力对管件截面精度的影响。
1 实验试件与方法
1.1 实验材料及管件
实验材料为汽车用SAPH440低碳钢和6063铝合金管坯。其中,SAPH440低碳钢管坯由薄板卷制而成,6063铝合金管坯由挤压工艺得到,初始外径0均为60 mm,壁厚0均为2 mm。利用管材液压成形性能实验装置(THF-160/50)对整管试样进行液压胀形,使管坯同时受到轴向和环向的拉应力,测试管坯在双轴应力下的力学性能,得到的等效应力应变曲线如图1所示,力学性能参数如表1所示。由表1可知,SAPH440低碳钢管和6063铝合金管的极限膨胀率分别为22.08%和17.67%。
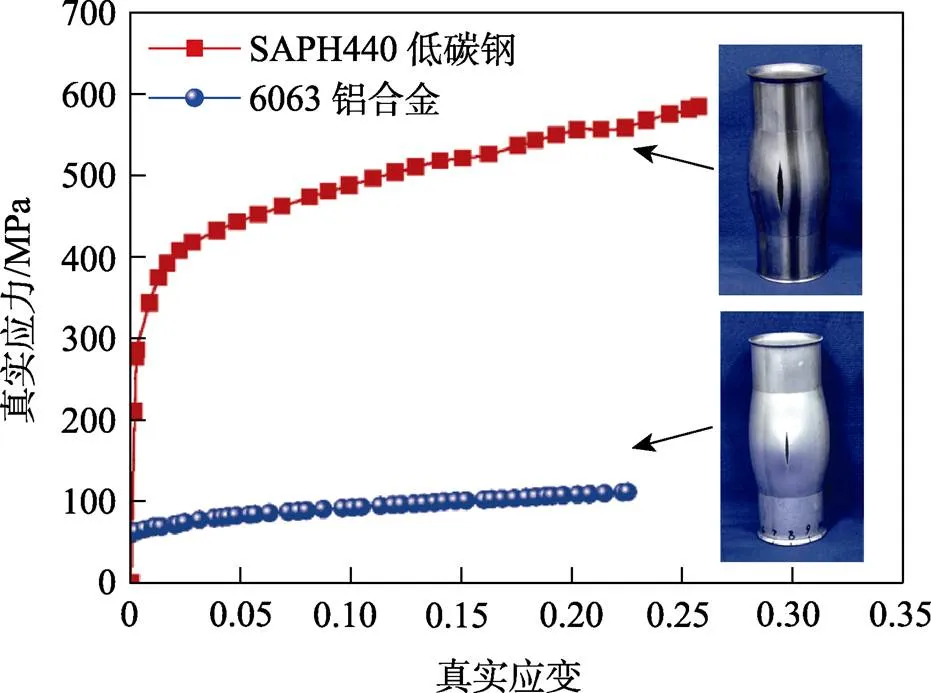
图1 管坯等效应力应变曲线
表1 管坯双轴应力力学性能参数
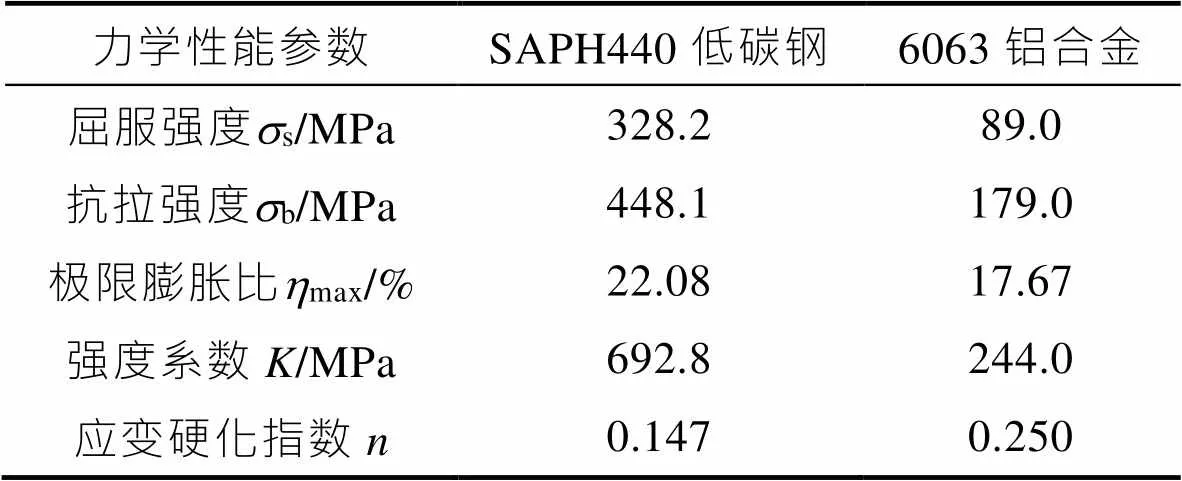
Tab.1 Mechanical property parameters of tube blanks under bi-axial stress state
对上述2种管坯进行变径管内高压成形实验。变径管的具体尺寸参数如图2所示,其中,成形区长度为120 mm(20),外径为69 mm,对应的膨胀率为15%,可以保证管坯完全贴靠模具型腔而不发生破裂。本研究主要讨论在不同合模力条件下,变径管中间横截面-处水平与竖直方向直径尺寸的变化。
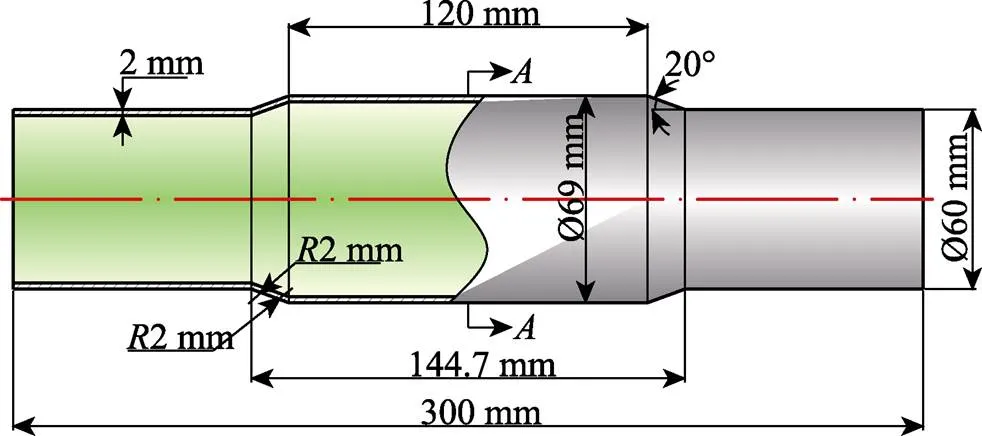
图2 变径管尺寸参数
1.2 实验装置
变径管的内高压成形实验装置如图3所示。该装置主要由实验模具、数据采集系统和控制系统3部分构成。其中,实验模具由上、下模及左、右密封冲头构成,上、下模的尺寸为300 mm×300 mm×100 mm(长×宽×高),总高为200 mm。在内高压成形实验过程中,通过锥形冲头将管端进行扩口,实现密封。实验在哈尔滨工业大学20 MN多轴数控内高压成形机平台上进行。

图3 变径管内高压成形实验装置
1.3 实验方案
在变径管内高压成形过程中采用恒定合模力的加载方式,如图4所示。即首先将合模力增加到设定值max(最大载荷),然后线性增加内压使管材发生胀形,增压过程中合模力保持恒定不变。当压力增至最大压力max后,保压5 s,然后卸载内压和合模力。
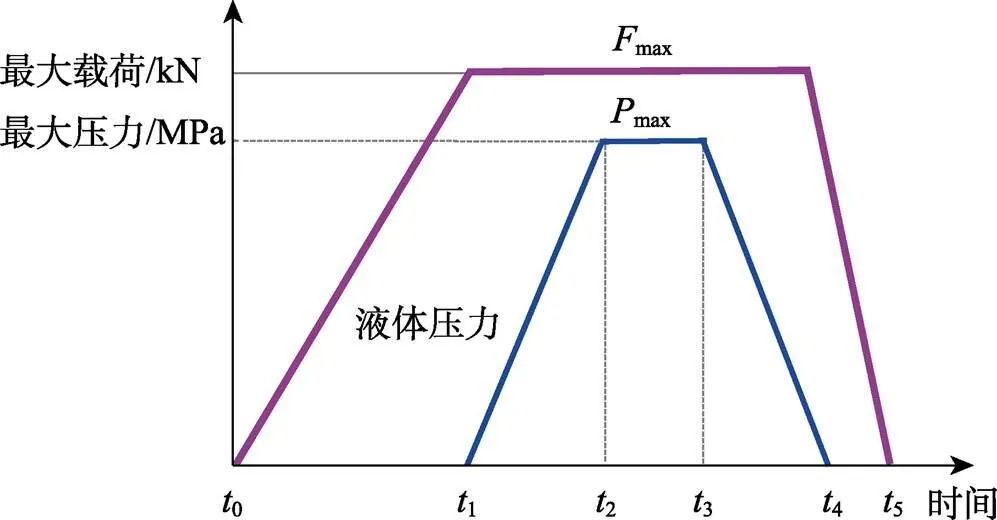
图4 恒定合模力加载曲线
具体实验方案如表2所示,主要利用两种不同的加载方式研究合模力对变径管截面尺寸的影响。方式1:内压线性加载到不同设定值,对应施加的合模力需保证内压加载至设定值时管材所受的合模力和液体反作用力之间的差值为恒定值,即max–max=200 kN,其中为液压作用面积,以研究变径管在不同内压条件成形时由合模力导致的管件横截面不圆度。方式2:内压线性加载到同一设定值,施加不同大小的合模力,以研究相同内压条件下合模力对变径管截面尺寸的影响。
表2 变径管内高压成形实验方案
Tab.2 Experimental scheme for hydroforming of variable-diameter tubular part
内高压成形结束,卸载内压并将管坯从模腔中取出后,管件发生回弹,利用游标卡尺测量得到变径管水平方向和竖直方向的直径1、2,如图5所示。
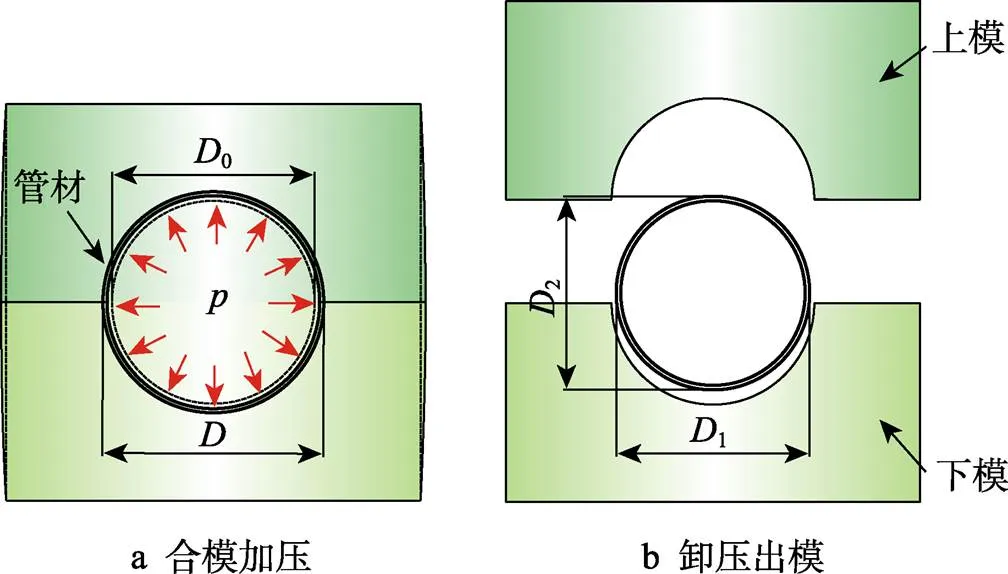
图5 变径管直径测量示意图
1.4 有限元模型
为研究变径管内高压成形过程中合模力对模具应力应变分布及模具型腔径向膨胀规律的影响,利用ABAQUS有限元分析软件进行模拟。建立变径管内高压成形有限元模型,如图6所示,该模型由管坯、上模、下模、上模板及下模板5部分组成。其中,管坯为三维可变形壳体,上、下模为三维可变形实体,其余部件均为离散刚体。将45钢的材料属性赋予上、下模:弹性模量207 GPa,泊松比0.3,屈服强度和抗拉强度分别为355和600 MPa。在模拟过程中,对下模板施加固定约束,对上模板施加合模力。管材网格尺寸设置为2 mm,选用S4R(四结点曲面薄壳或厚壳,减缩积分,沙漏控制,有限膜应变)网格单元;模具网格尺寸设置为4 mm,选用C3D8R(八结点线性实体,减缩积分,沙漏控制)网格单元。
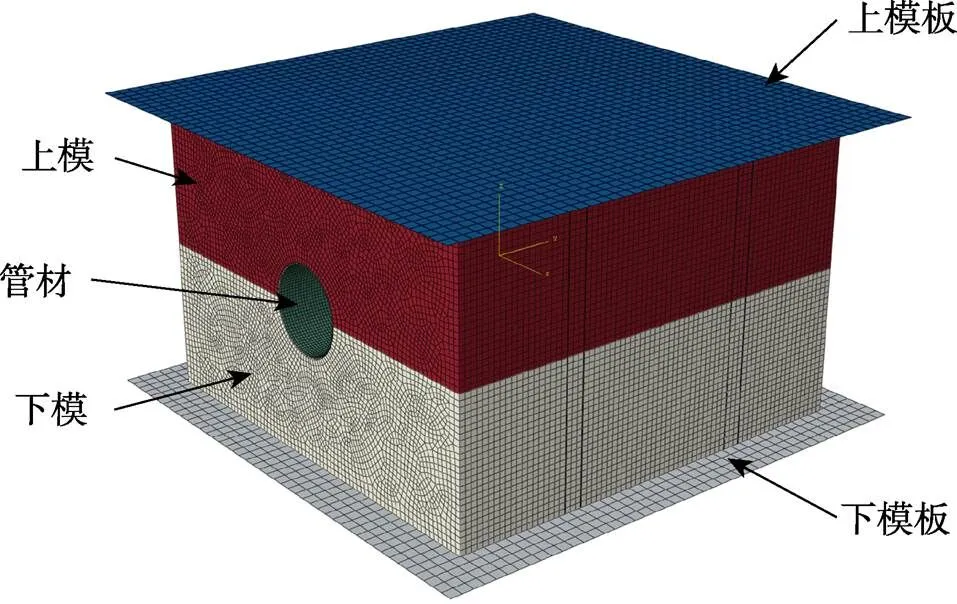
图6 变径管内高压成形有限元模型
2 结果与讨论
2.1 变径管截面尺寸精度分析
在变径管内高压成形后,卸载内压并开模,管件会发生一定量的回弹。因此,可以控制内压使模具产生一定量的弹性变形,当模具胀形量恰好能够补偿管件的回弹量时,能够显著改善管件截面的尺寸精度。在不同内压条件下测得的变径管截面尺寸变化规律如图7所示。可以看出,管件的截面尺寸均随内压增加而增大。当内压为150 MPa时,SAPH440低碳钢变径管截面水平方向的直径1(图5a)达到设计值。同理,对于6063铝合金变径管,当内压为45 MPa时,截面水平方向直径1(图5b)达到设计值。然而,管件竖直方向直径2始终小于水平方向直径1。对于SAPH440低碳钢管,截面在水平、竖直两方向的平均直径相差0.08~0.18 mm;对于6063铝合金管,两者相差0.06~0.18 mm。
产生这种现象的主要原因是,成形过程中施加的合模力会导致模具型腔发生弹性变形,被压成非圆形,进而导致变径管水平方向直径1增大、竖直方向直径2减小。SAPH440低碳钢和6063铝合金变径管的截面不圆度如图8所示,最大不圆度分别达到0.27%和0.26%。因此,变径管截面不同方向的尺寸无法同时达到设计值。对于SAPH440低碳钢变径管,当内压加载至150 MPa时,水平方向上的直径尺寸1达到设计值69.00 mm,而竖直方向直径2仅为68.82 mm。通过上述对两种变径管截面不圆度的分析可知,合模力对内高压成形管件截面形状精度的影响是不可避免的。在实际成形过程中,在保证上、下模闭合的前提下,应尽可能减小合模力或者改用随内压可变的合模力加载方式。此时,需施加更高的内压,以使管件水平方向直径尺寸达到设计值。
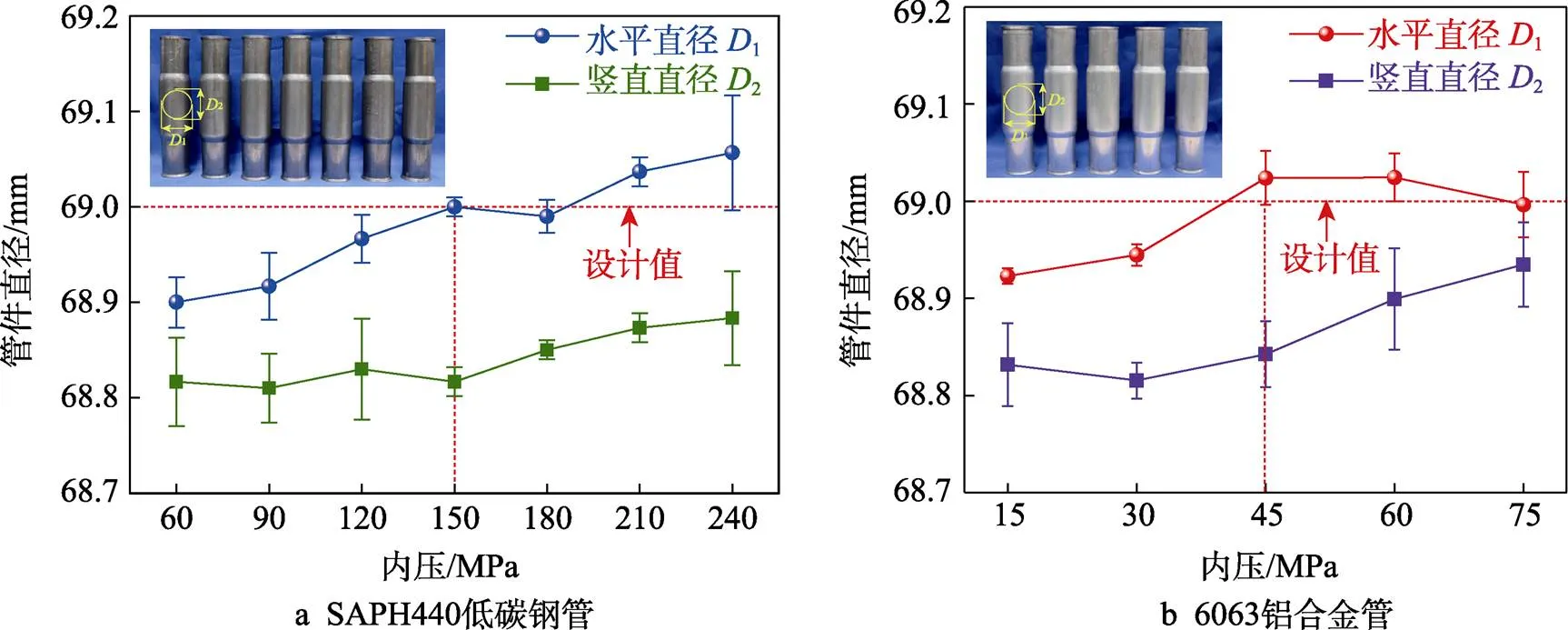
图7 不同内压条件下变径管的截面直径
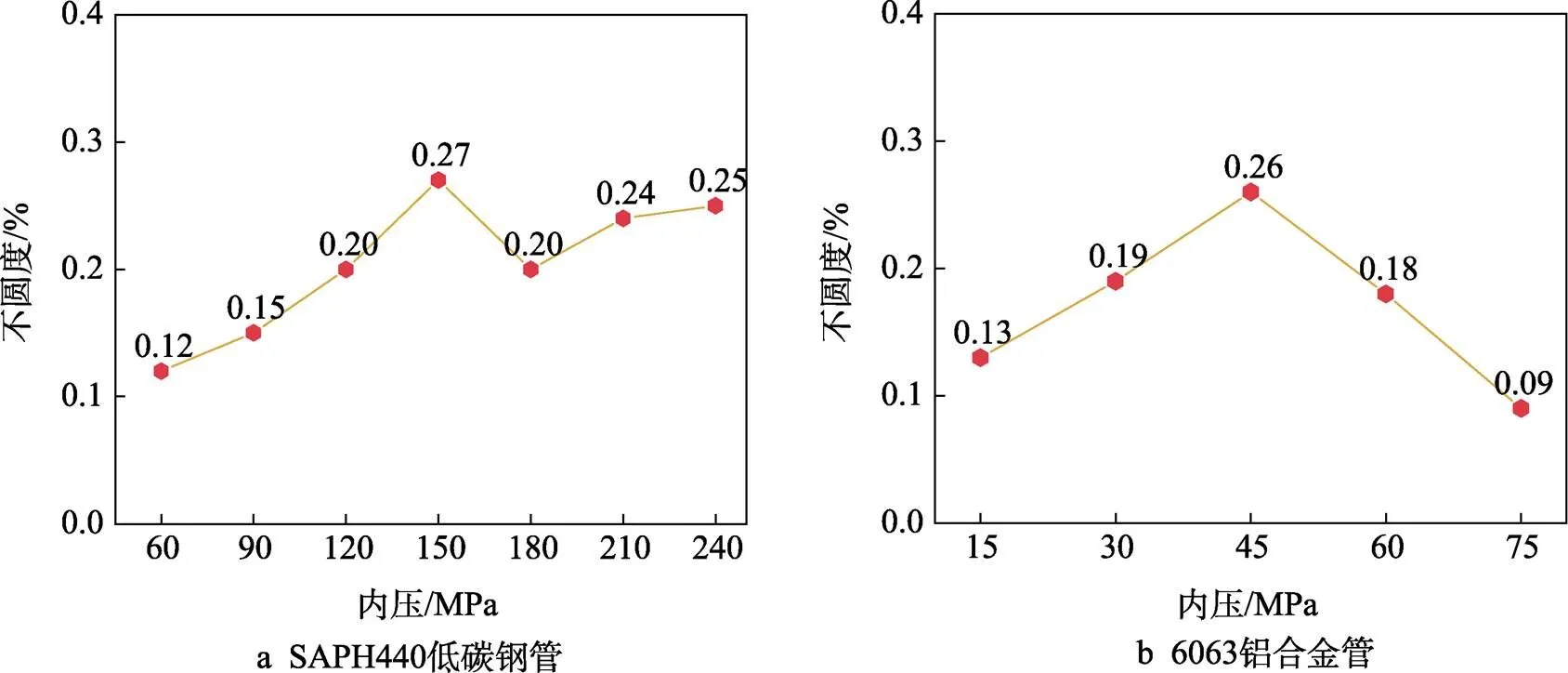
图8 不同内压条件下变径管的截面不圆度
2.2 合模力对变径管截面不圆度的影响
不同合模力条件下变径管水平和竖直方向的直径1、2如图9所示。可以看出,对于SAPH440低碳钢管,在相同内压条件下,随着合模力的增加,变径管水平方向直径1变化很小,而竖直方向直径2呈减小趋势,竖直方向直径比水平方向小0.15~ 0.20 mm。对于6063铝合金管,随着合模力的增加,变径管水平方向直径1与竖直方向直径2的变化没有固定规律,两者相差0.05~0.17 mm。
根据图9计算得到的不同合模力条件下变径管的截面不圆度如图10所示。可以看出,对于SAPH440低碳钢变径管,截面不圆度在0.21%~0.29%范围内,整体呈现出随合模力增加而增大的趋势;而6063铝合金变径管的截面不圆度在0.06%~0.18%范围内,相比SAPH440低碳钢管,其不圆度整体较小,且无明显变化规律。这可能是因为,本研究中的模具尺寸较大,当合模力在800~2 000 kN范围内变化时,模具受到的应力较小,由合模力引起的6063铝合金变径管截面形状畸变大部分处于弹性变形状态,卸压开模后发生了弹性回复。因此,图10b中6063铝合金变径管截面不圆度的差异实际上并不是由合模力导致的,而是由管坯自身的力学性能差异引起的。
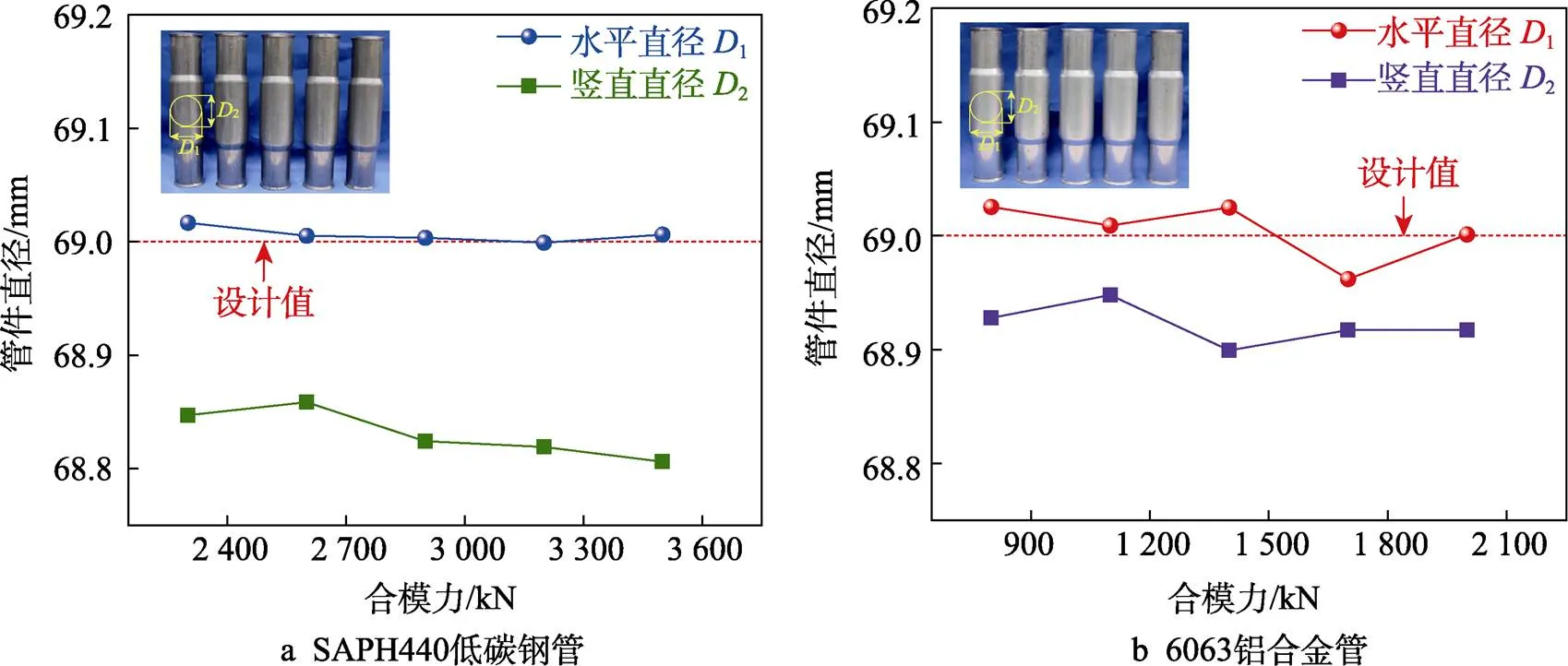
图9 不同合模力条件下变径管的截面直径
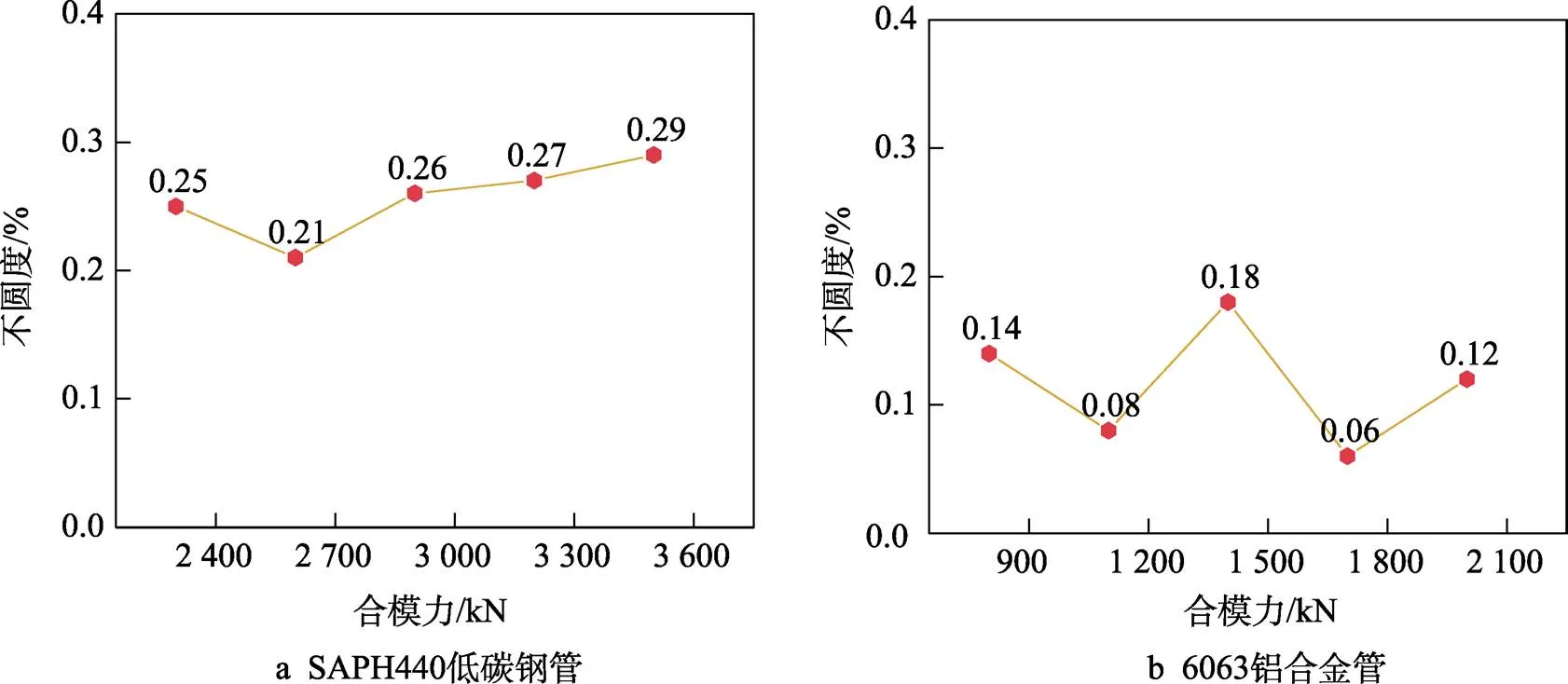
图10 不同合模力条件下变径管的截面不圆度
2.3 模具应力及变形规律
不同内压下,SAPH440低碳钢变径管在内高压成形过程中模具的应力分布规律如图11所示。随着内压的增加,模具型腔内部的Mises应力逐渐增大,模腔上、下侧的Mises应力高于左、右侧。当内压加载至240 MPa时,模具内部应力达到最大值386 MPa,最大应力点位于模腔两侧的过渡角处。分析变径管中间横截面–处模具型腔表面上的Mises应力可知,当内压加载至240 MPa时,–截面上的最大Mises应力为311 MPa,低于45钢的屈服强度,表明此时模具型腔仍处于弹性变形状态。
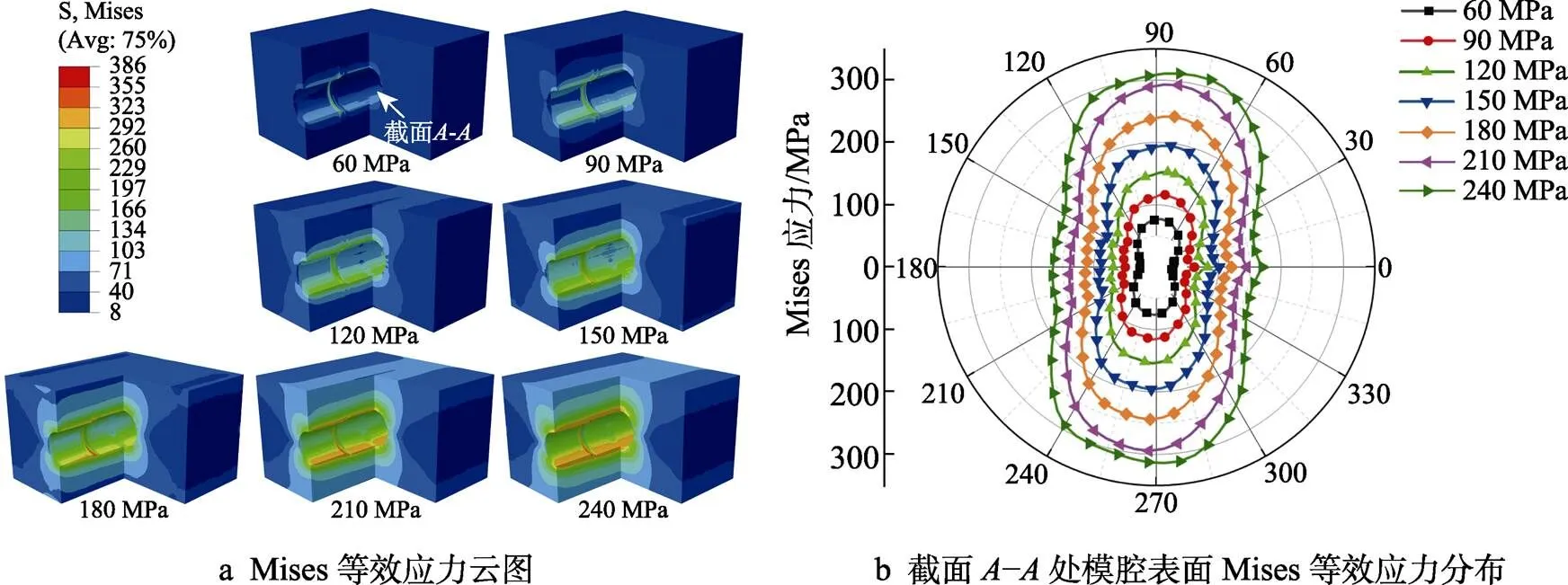
图11 SAPH440低碳钢变径管内高压成形模具应力分布
不同内压条件下,中间横截面–处模具型腔表面的径向位移分布如图12所示。可以看出,模腔顶部的径向位移最小,水平分型面附近的径向位移最大。当内压加载至60 MPa时,模腔顶部和底部的径向位移分别为–0.012和0.008 mm,水平方向的最大径向位移为0.014 mm,表明模腔顶部在合模力的作用下发生了一定的下移。当内压加载至240 MPa时,模腔顶部的径向位移为0.002 mm,水平方向最大径向位移为0.064 mm。随着内压的增加,模腔表面在水平和竖直方向上的径向位移逐渐增大,但由于成形过程中模具顶部施加有合模力,模腔竖直方向的径向位移始终小于水平方向。因此,在卸载内压和合模力后,管件竖直方向径向变形量小于水平方向,如图13所示,进一步说明了变径管内高压成形过程中合模力会影响截面的形状精度与尺寸精度。
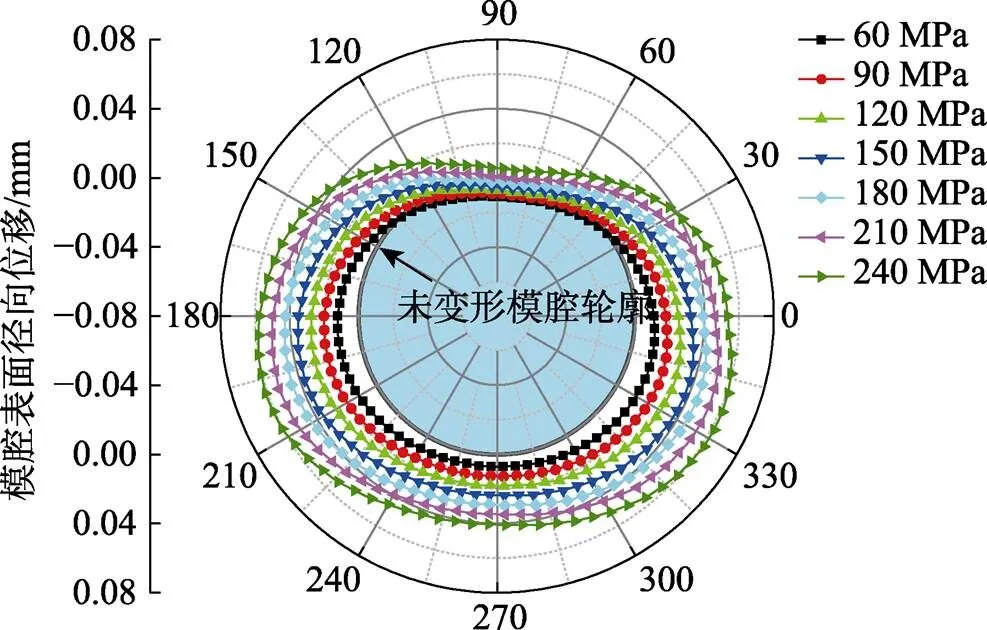
图12 不同内压条件下模腔表面的径向位移
综上所述,在恒定合模力加载方式下,合模力是影响变径管截面精度(不圆度)的重要因素,管件截面不圆度随合模力的增加而增大。可通过增大模具尺寸以减小模具变形来克服上述问题,但增大模具尺寸会导致模具体积庞大,大幅增加模具的材料与加工成本。对于大尺寸管件,即使增大模具尺寸,也无法从根本上解决恒定合模力加载导致模具变形对其寿命和管件截面精度产生影响的问题,需采用可变合模力加载方式,以降低合模力对管件截面精度的影响,这成为目前的重点研究方向。
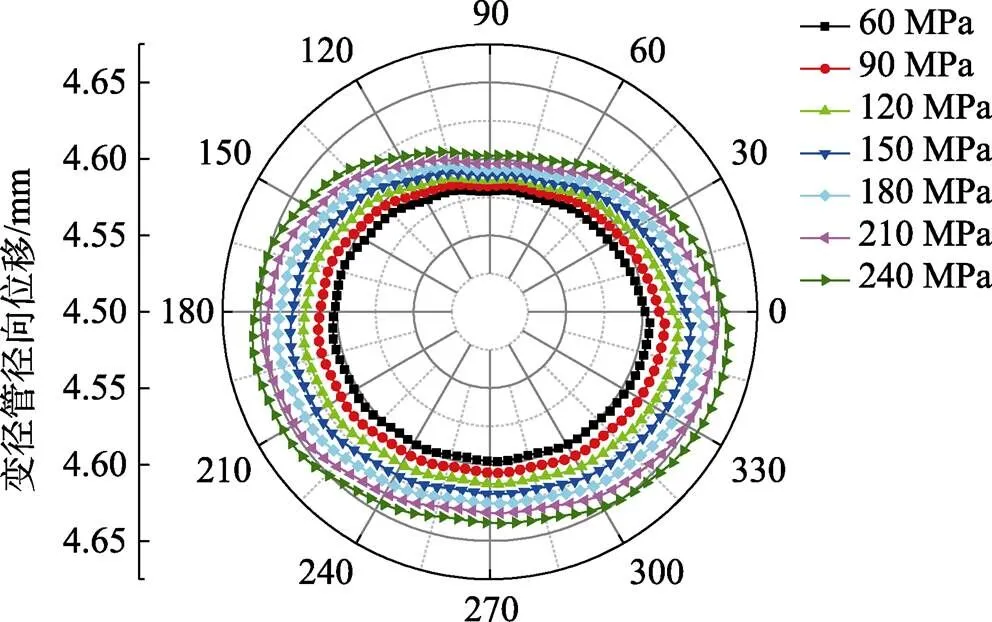
图13 不同内压条件下变径管的径向位移
3 结论
通过内高压成形实验与数值模拟,研究了SAPH440低碳钢和6063铝合金变径管的截面精度问题,得到以下结论。
1)在不同内压条件下成形变径管时,合模力会不可避免地对管件截面精度产生影响,导致截面竖直方向的直径始终小于水平方向,管件产生一定的不圆度。SAPH440低碳钢和6063铝合金变径管的最大截面不圆度分别为0.27%和0.26%。
2)在相同内压下成形时,随着合模力的增加,SAPH440低碳钢和6063铝合金变径管的截面不圆度分别在0.21%~0.29%和0.06%~0.18%范围内变化。
3)变径管内高压成形时,在合模力的作用下,模腔上、下侧的Mises等效应力高于左、右侧。模腔顶部的径向位移最小,分型面附近的径向位移最大,模腔被压扁,导致卸载内压和合模力后管件竖直方向的直径始终小于水平方向。
[1] POIANA D I, IONEL I, POPA R M, et al. Results Concerning Manufacturing of Tubular Car Components Using Hydroforming and Hydroperforation Processes[J]. IOP Conference Series: Materials Science and Engineering, 2022, 1220(1): 012038.
[2] ASHWAK A, BHIL A, MANJUNATH V B. A Review on Tube Hydroforming (THF) Technology for Automotive Application[J]. International Research Journal of Multidisciplinary Technovation, 2019: 11-18.
[3] ZHANG S H, CHEN D Y, XU Y, et al. Robust Hydroforming Technologies to Enhance the Formability of Sheet and Tube[C]. Proceedings of the 13th International Conference on the Technology of Plasticity:Forming the Future, The Minerals, Metals & Materials Series, 2021: 353-365.
[4] 苑世剑. 现代液压成形技术[M]. 2版. 北京: 国防工业出版社, 2016.
YUAN Shi-jian. Modern hydroforming technology[M]. 2nd ed. Beijing: National Defense Industry Press, 2016.
[5] HWANG Y M, MANABE K I. Latest Hydroforming Technology of Metallic Tubes and Sheets[J]. Metals, 2021, 11(9): 1360.
[6] BELL C, CORNEY J, ZUELLI N, et al. A State of the Art Review of Hydroforming Technology[J]. International Journal of Material Forming, 2020, 13(5): 789-828.
[7] 郭训忠, 陶杰, 王辉. 航空导管先进成形技术的研究进展[J]. 南京航空航天大学学报, 2020, 52(1): 12-23.
GUO Xun-zhong, TAO Jie, WANG Hui. Research Progress on Aadvanced Forming Technology for Aviation Tube[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2020, 52(1): 12-23.
[8] 李光霁, 刘新玲. 汽车轻量化技术的研究现状综述[J]. 材料科学与工艺, 2020, 28(5): 47-61.
LI Guang-ji, LIU Xin-ling. Literature Review on Research and Development of Automotive Lightweight Technology[J]. Materials Science and Technology, 2020, 28(5): 47-61.
[9] HAN C, LIU Q, LU H, et al. Thickness Improvement in Hydroforming of a Variable Diameter Tubular Component by Using Wrinkles and Preforms[J]. The International Journal of Advanced Manufacturing Technology, 2018, 99(9): 2993-3003.
[10] LIU Jing, LV Zhi-yong, LIU Yang, et al. Deformation Behaviors of Four-Layered U-Shaped Metallic Bellows in Hydroforming[J]. Chinese Journal of Aeronautics, 2020, 33(12): 3479-3494.
[11] CUI Xiao-lei, TENG Bu-gang, YUAN Shi-jian. Hydroforming Process of Complex T-Shaped Tubular Parts of Nickel-Based Superalloy[J]. CIRP Journal of Manufacturing Science and Technology, 2021, 32: 476-490.
[12] 崔晓磊. 管材流体高压成形起皱行为与皱纹控制研究进展[J]. 机械工程学报, 2021, 57(12): 226-236.
CUI Xiao-lei. Research Progress on Wrinkling Behavior and Wrinkles Control for Tube Hydroforming[J]. Journal of Mechanical Engineering, 2021, 57(12): 226-236.
[13] NAKAMORI T, SHUKUNO K, MANABE K. In-Process Controlled Y-Shape Tube Hydroforming with High Accurate Built-in Sensors[J]. Procedia Engineering, 2017, 184: 43-49.
[14] 蔡洋, 刘强, 王小松, 等. 内高压成形制备6063铝合金异形管件的壁厚分布及尺寸精度[J]. 中国有色金属学报, 2015, 25(9): 2372-2380.
CAI Yang, LIU Qiang, WANG Xiao-song, et al. Thickness Distribution and Size Deviation of 6063 Alloy Irregular Tubular Parts Prepared by Hydroforming[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(9): 2372-2380.
[15] 陈名涛, 肖小亭, 周富强. 单侧并列双支管内高压成形应力与应变分析及金属流动研究[J]. 锻压技术, 2021, 46(4): 106-111.
CHEN Ming-tao, XIAO Xiao-ting, ZHOU Fu-qiang. Research on Stress, strain and Metal Flow in Hydroforming for Unilateral Parallel Double Branch Tube[J]. Forging & Stamping Technology, 2021, 46(4): 106-111.
[16] VOLLERTSEN F. Accuracy in Process Chains Using Hydroforming[J]. Journal of Materials Processing Technology, 2000, 103(3): 424-433.
[17] 韩聪, 贺久强, 苑世剑. 780MPa超高强钢扭力梁内高压成形研究[J]. 精密成形工程, 2016, 8(5): 53-59.
HAN Cong, HE Jiu-qiang, YUAN Shi-jian. Hydroforming of an Automotive Torsion Beam with 780 MPa Advanced High Strength Steel[J]. Journal of Netshape Forming Engineering, 2016, 8(5): 53-59.
[18] 蔡洋, 王小松, 苑世剑. 预弯对铝合金管材内高压成形缺陷与尺寸精度的影响[J]. 材料工程, 2017, 45(9): 108-115.
CAI Yang, WANG Xiao-song, YUAN Shi-jian. Effects of Pre-Bending on Defect and Dimensional Precision in Hydroforming of Aluminum Alloy Tube[J]. Journal of Materials Engineering, 2017, 45(9): 108-115.
[19] 李彩霞, 张晓峰, 王敬. 预弯工艺及摩擦系数对管材内高压成形的影响[J]. 锻压技术, 2018, 43(11): 48-53.
LI Cai-xia, ZHANG Xiao-feng, WANG Jing. Influences of Pre-Bending Process and Friction Coefficient on Tube-Hydroforming[J]. Forging & Stamping Technology, 2018, 43(11): 48-53.
[20] 崔晓磊, 韩聪, 苑世剑. 加载条件对内高压成形管件尺寸精度的影响[J]. 材料科学与工艺, 2020, 28(3): 150-156.
CUI Xiao-lei, HAN Cong, YUAN Shi-jian. Effect of Loading Conditions on Dimension Accuracy of Hydroformed Tubular Parts[J]. Materials Science and Technology, 2020, 28(3): 150-156.
[21] HARTL C, ANYASODOR G, PTASCHLIK T, et al. Investigation into Reduction of Die-Cavity Deflection in Micro-Hydroforming Processes Using FEA[J]. The International Journal of Advanced Manufacturing Technology, 2010, 47(9): 853-858.
Influence of Clamping Force on Dimensional Accuracy of Variable-diameter Tubular Part in Hydroforming
CUI Xiao-leia,b, WANG Yi-chunb, WEN Shi-yub, XU Wang-chengb
( a. National Key Laboratory for Precision Hot Processing of Metals; b. School of Materials Science and Engineering, Harbin Institude of Technology, Harbin 150001, China)
During the hydroforming process, an unreasonable loading of clamping force will not only reduce the life of forming die, but also easily cause the sectional dimension accuracy of tubular parts to be out of tolerance. It is necessary to investigate the influence of clamping force on the sectional dimension of tubular parts to improve this defect. Experiment of hydroforming and numerical simulation of variable-diameter tubular parts with low carbon steel and aluminum alloy were carried out, the influence law of clamping force on sectional dimension accuracyunder two different loading conditions was analyzed. The results show that the equivalent stress on the upper and lower sides of the die cavity is higher than that on the left and right sides in the hydroforming process of the variable-diameter tubular parts. The radial displacement at the top of the die cavity is the smallest, while near the parting surface is the largest. The die cavity is pressed to be oblate by clamping force, leading to the fact that the vertical diameter of the tubular part's section is always smaller than the horizontal diameter after unloading the internal pressure and clamping force, resulting in a certain degree of out-of-roundness. The maximum out-of-roundness of variable-diameter tubular parts with SAPH440 low carbon steel and 6063 aluminum alloy are 0.27% and 0.26%, respectively. It shows that in the hydroforming process, the influence of clamping force on the section accuracy is inevitable. It is necessary to reduce its influence by increasing the size of the die or using a loading method with variable clamping force.
hydroforming; variable-diameter tubular part; clamping force; dimensional accuracy; out-of-roundness
10.3969/j.issn.1674-6457.2022.10.002
TG394
A
1674-6457(2022)10-0012-07
2022–05–07
中国博士后科学基金(2020M670907);黑龙江省博士后基金(LBH-Z20017);国家自然科学基金(51805357)
崔晓磊(1986—),男,博士,讲师,硕士生导师,主要研究方向为薄壁管流体压力成形理论与技术。
