AlCl分子低激发态光谱性质的从头计算研究

国慧杰，桑纪群，姜 文，李 瑞,任晓辉，艾瑞波

(齐齐哈尔大学 理学院，黑龙江 齐齐哈尔 161006)

近年来，单卤化铝在分子激光冷却方面的潜在应用引起了人们越来越多的关注。一氯化铝(AlCl)是一种天体分子，Cernicharo等人于1987年在天体环境中检测到AlCl的存在[1]。在化学方面AlCl被认为是一种非常有效且经济的还原剂，可以用来生产光伏级硅[2,3]。此外，AlCl的光谱特性可用于监测饮用水中的氯含量[4]。AlCl的电子结构和光谱性质的实验和理论研究非常重要。

在实验方面，1934年Bhaduri[5]等人对AlCl进行了早期光谱研究。Reddy[6]测得了该体系10个波段在真空紫外区中的跃迁。Wyse[7]测量了基态在毫米波区域的转动谱，并进行了相应的光谱分析。Dearden[8]使用332～570 nm激光共振增强光电离光谱技术研究了24000～60000 cm-1的高激发电子态，研究了AlCl分子电子态的光谱常数。此外，Saksena[9]在高分辨率光谱仪下观察a3Π-X1Σ+跃迁，并确定了a3Π态的转动常数。Mahieu[10]研究了A1Π-X1Σ+跃迁，获得了这两种态的精确转动常数和振动常数，并讨论了在v′=10振动能级下A1Π态的预解离。1987年，Rogowsiu[11]通过激光诱导荧光技术确定了AlCl分子A1Π态的辐射寿命。Lide[12]应用高温谱仪研究了AlCl的跃迁并得到光谱常数。

理论方面，Brites[13]等人利用MRCI方法计算了AlCl分子电子态势能曲线及光谱常数，研究了该体系的跃迁偶极矩，并预测了A1Π态的辐射寿命。Langhoff[14]等人采用从头计算方法计算AlCl的光谱常数，并得到了AlCl分子的A1Π态的v′=0振动能级的辐射寿命。在2016年，杨等人[15]使用ACVQZ基组研究了X1Σ+，a3Π和A1Π态的势能曲线，永久偶极矩和跃迁偶极矩等光谱性质。Petrie[16]采用G2理论计算了AlCl分子基态的Re和De值。Wilson[17]利用耦合簇理论[CCSD(T)]，计算了包括AlCl在内的几种分子的基态Re和De值。Hamade[18]计算了12种态的PECs并预测了光谱参数。Wan[19]采用从头计算方法研究了AlCl分子的电子结构以及激光冷却的可行性。Daniel[20]和张[21]等人采用从头计算方法研究了A1Π-X1Σ+的跃迁，以及电子态的电子结构。

综上所述，对AlCl分子的低激发电子态进行了一系列研究。关于低激发态的电子结构和光谱信息仍然较为有限，精确度需要进一步提高。在这里，本文基于高精度的MRCI+Q方法对AlCl分子的电子态进行理论研究，给出了最低解离极限相关的12个Λ-S态的PECs。基于计算的PECs，获得束缚态光谱常数。并对PDMs，SO矩阵元，TDMs，FCFs和辐射寿命进行计算。

1 计算方法

本文使用由Werner等人开发的量子化学程序包MOLPRO[22]对AlCl分子最低解离极限Al(2Pu)+Cl(2Pu)的12个电子态进行从头计算研究。计算中Al和Cl原子均采用aug-cc-pwCVQZ-dk基组[23-25]。为了能够获得精确的低激发电子态的电子结构，在本次计算中通过以下三个步骤进行：第一步，采用HF自洽场方法对AlCl分子的基态(X1Σ+)波函数进行计算，在HF方法获得的波函数基础上采用完全活性空间自洽场(CASSCF)方法对获得的基态波函数进行优化。最后在CASSCF波函数基础上，采用MRCI[26]方法来获得高精度的能量和波函数。在计算过程中为了保证精度，采用戴维森修正(Dacidson(+Q))[27]来修正MRCI方法的大小不一致性。

由于MOLPRO程序自身的局限性，采用了C∞v点群的阿贝尔子群C2v群的不可约表示来描述，二者之间的不可约表示对应关系为：Σ+=A1，Π=B1+B2，Δ=A1+A2，Σ-=A2。AlCl选择4a1、2b1、2b2分子轨道作为活性空间来构建电子态波函数。在MRCI计算中，AlCl分子活性空间的分子轨道对应Al的4s4p壳层以及Cl的3s3p壳层。Al内部的1s2s2p电子和Cl内部的1s2s2p电子被放置在闭壳层中。

基于MRCI+Q方法获得的AlCl分子的12个Λ-S态的势能曲线，利用LEVEL[28]程序数值求解薛定谔方程获得AlCl分子的光谱常数。同时基于计算获得的数据绘制出了AlCl分子的DMs、TDMs以及SO矩阵元随核间距变化的曲线。同时计算出的AlCl分子FCFs对应的振动能级的信息，并将11Π-X1Σ+的FCFs绘制成柱状图进行讨论。基于计算获得的FCFs和TDMs，计算了态与态之间跃迁的辐射寿命。

2 研究结果

2.1 AlCl分子的光谱性质

采用MRCI+Q的方法计算出AlCl分子最低解离极限Al(2Pu)+Cl(2Pu)的12个Λ-S态。该解离极限对应的电子态为：X1Σ+、21Σ+、11Σ-、11Π、21Π、11Δ、13Σ+、23Σ+、13Σ-、13Π、23Π和13Δ，其中有6个单重态，6个三重态。为了能够清楚地看到AlCl分子能量和核间距之间的关系，将其二者的关系绘制于图1中，其中(a)为单重态，(b)为三重态。从图1中可以看到，X1Σ+、11Π和13Π是典型的束缚态，具有较深的势阱。在核间距R=2.5 Å时，13Σ+和23Σ+态之间存在避免交叉点，导致23Σ+态形成势阱，13Σ+态出现势垒。

实验.a[30]，实验.B[29]，实验.c[32]，理论.d[31]，理论.e[14]，理论.f[15]，理论.G[21]，理论.h[19]，理论.i[16]，理论.j[13]

表1中基态X1∑+的平衡核间距Re为2.141 7Å，与实验值[29,30]的误差仅为0.011 6Å(0.5%)。基态的De实验值为5.15eV[29]，理论值在5.17～5.27eV范围[13-16,19,21,31]，本文的计算值5.22eV与Yang等人[15]的计算结果吻合较好。对于X1∑+和11Π，两者平衡核间距非常接近差值为0.003 Å，所以X1∑+和11Π跃迁的FCFs高度对角化，将在后面讨论。从图1中可以看到，这两个电子态的PECs形状也非常相似。

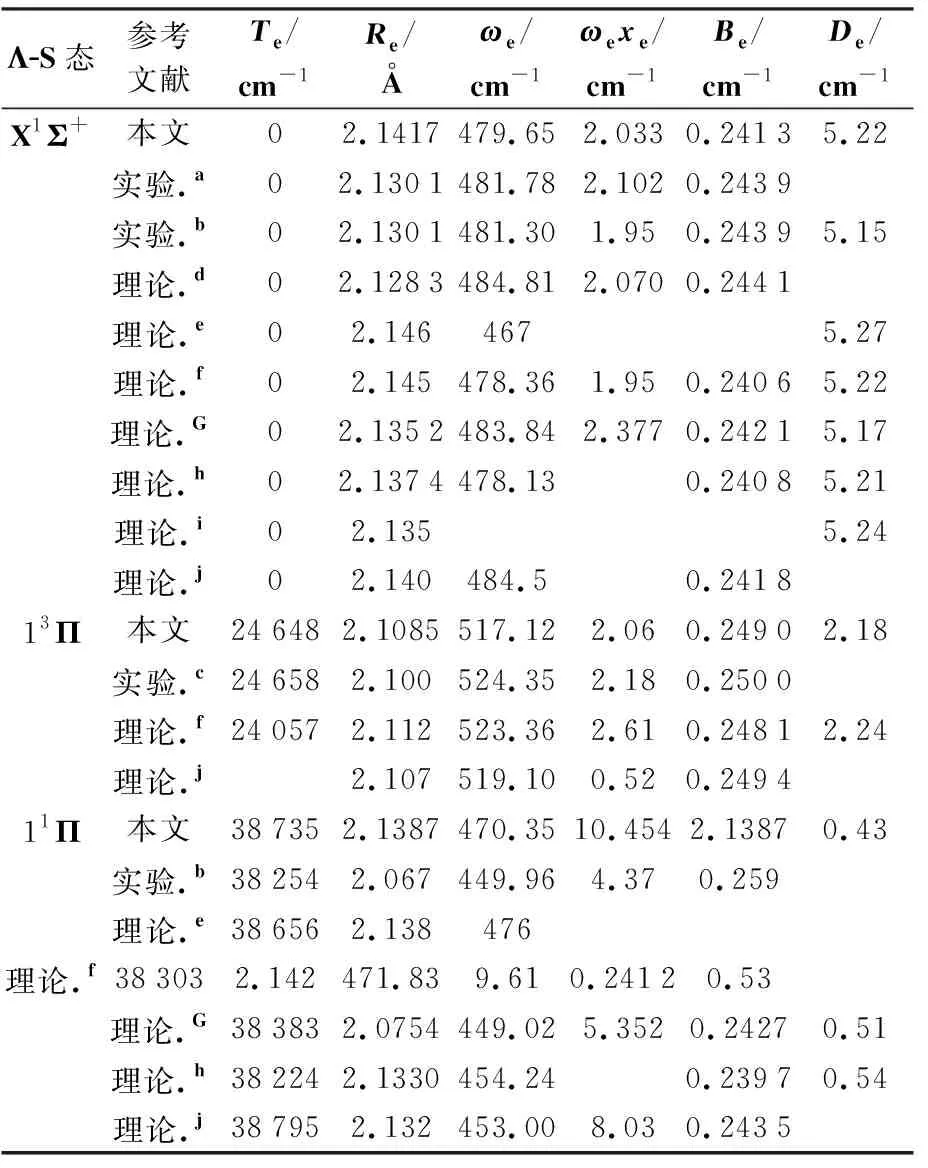
表1 AlCl分子L-S态的光谱常数

从图1中可以观察到11Δ和11Σ-的势能曲线几乎重合，13Δ和13Σ-的势能曲线几乎重合，21∑+与11Δ和11Σ-势能曲线相交，23∑+与13Δ和13Σ-势能曲线相交，这些交叉的态之间可能会发生很强的相互作用。11Π和13Π态的解离能为0.43eV和2.18eV。对于11Π态，计算的Te和ωe值为38 735cm-1和470.35cm-1，与先前的实验值[29]38254和449.96cm-1符合得很好，误差分别在1.3%和4.5%之内。本次工作计算Re的结果与其他理论和测量值之间的误差均小于3%。对于13Π的Te、ωe、Be和Re值分别为24 648、517.12、0.249 0cm-1和2.108 5Å，与实验结果[30]24 658cm-1、524.35cm-1、0.250 0cm-1和2.100Å相一致，偏差分别为0.04%、1.4%、0.4%和0.4%。

图1 AlCl分子Λ-S态的势能曲线

图2 AlCl分子Λ-S态DMs随核间距的变化关系

如图2所示，基于MRCI波函数，计算了12个Λ-S态在核间距2.0-6.0 Å范围的DMs随核间距的变化关系曲线。从图中可以看出这些态的DMs随着核间距的增加逐渐趋于零，证实了解离产物均为中性原子。在图2中可以发现X1∑+的电偶极距在R=4.5 Å时存在极小值为-4.722 12a.u.。而11Δ和11∑-以及13Δ和13∑-的电偶极距变化规律近似。

图3中绘制了与13Π态和11Π态交叉区域势能曲线图。可以看出电子态之间存在交叉。为了阐明AlCl分子各个电子态之间的强相互作用，将计算得到的电子态之间的自旋轨道矩阵元|Hso|绘制于图4中。11Π和13∑+、13∑-和13Δ以及11Π和13∑+电子态在核间距R=2.8～3.2Å之间，能量范围在42 000cm-1和43 000cm-1之间存在交叉。11Π和13∑+、13∑-和13Δ以及11Π和13∑+电子态处于交叉点时SO矩阵元分别在17、130、134cm-1附近。由于13Π和13∑+电子态的势能曲线在核间距R=3.4～3.5 Å之间发生了交叉，处于交叉点时SO矩阵元在70cm-1附近。从图4中可以看出，SO矩阵元整体趋势先增加到极大值然后逐渐减小趋于水平。

图3 与13Π态和11Π态交叉区域势能曲线

图4 AlCl分子SO矩阵元随核间距的变化关系

2.2 AlCl分子跃迁性质

在图5中绘制了AlCl分子13Σ+-13Π和11Π-X1Σ+之间的跃迁偶极距随核间距R的变化曲线。从图中可以看出随着核间距R逐渐增大，13Σ+-13Π和11Π-X1Σ+之间的跃迁偶极距均趋向于0。对于13Σ+-13Π跃迁，TDM曲线随着键长急剧下降；而11Π-X1Σ+跃迁，TDM曲线随着键长增大而增大。利用TDMs以及FCFs计算11Π态的辐射寿命。

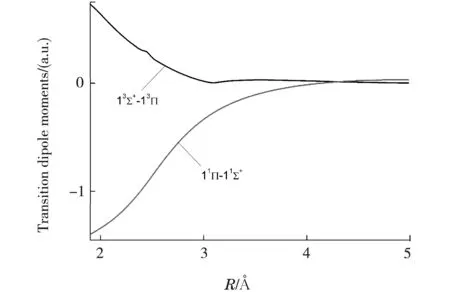
图5 AlCl分子13Σ+-13Π和11Π-X1Σ+态TDMs随核间距的变化关系

利用LEVEL程序计算了11Π-X1Σ+跃迁的FCFs，并将计算结果列于表2中。通过表中数据可以看出本次计算的FCFs与其他理论计算的结果吻合程度较高。11Π-X1Σ+的FCFs呈现出高度对角化的变化趋势。为了方便分析，将振动能级ν′=0到ν′=5和ν″=0到ν″=5以柱状图的形式绘制于图6中。从图1中可以看出11Π和X1Σ+的势能曲线形状相似，且拥有相近的平衡核间距，这意味这些态的FCFs是高度对角化的，这有利于激光制冷中的光循环的闭合。

表2 11Π-X1Σ+之间跃迁的Franck-Condon因子

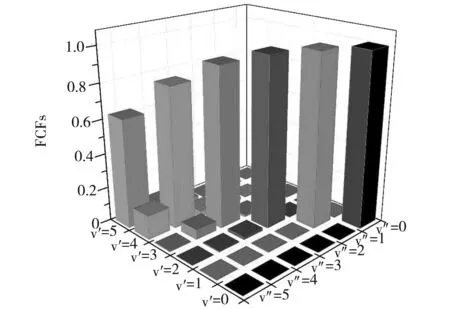
图6 11Π-X1Σ+的FCFs和振动能级之间的关系

利用电子态之间的TDM、FCFs以及振动能级之间的能量差，根据如下公式对电子态的辐射寿命进行计算，公式如下：

在这个式子中，qν′ν″代表Franck-Condon因子；TDM代表跃迁偶极距的平均值，其单位是原子单位(a.u.)；ΔEν′ν″代表的是振动能级ν′和ν″之间的能级差；τ代表辐射寿命，单位是秒(s)。计算出的结果在表3中列出，本次计算的结果与其他实验和理论结果在同一数量级且非常吻合，本次计算在实验误差范围内。从表中可以看出理论值均随振动能级的增加而递增。因为其具有较短的辐射寿命和高度对角化的Franck-Condon因子，可作为激光制冷的目标分子。

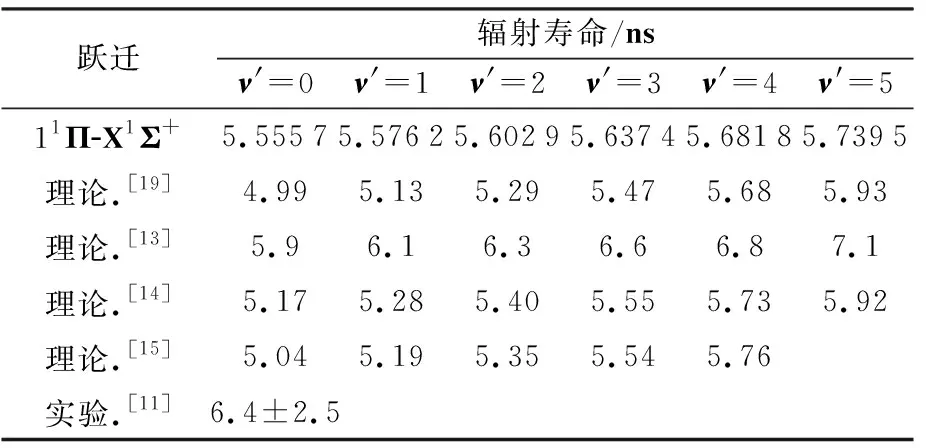
表3 11Π-X1Σ+之间跃迁辐射寿命

3 结 语

本文采用MRCI+Q方法对对AlCl分子的电子态和光谱性质进行了详细的理论研究，结果与实验值吻合较好。获得了Λ-S态的势能曲线和光谱常数，DMs以及SO矩阵元。揭示了各种曲线交叉和避免交叉。此外，还获得了TDMs、FCFs和辐射寿命等跃迁特性。本文的工作对在理论上寻找激光冷却候选分子，以及深入理解电子激发态的结构和动力学相关性质具有一定的参考意义。