基于高斯-柯西变异海鸥优化算法的柴油机共轨压力控制研究

李进龙，王贵勇，王煜华，邓冬荣，赵 友，何述超

（1.昆明理工大学 云南省内燃机重点实验室，昆明 650500；2.柳州职业技术学院，柳州 545616；3.昆明云内动力股份有限公司，昆明 650500）

0 概述

高压共轨系统是目前应用最广泛的柴油机燃油喷射系统，其具有转速和喷油可独立控制、高喷射压力、喷油量和喷油正时灵活可调等特点，能达到优化缸内燃烧和降低排放的目的［1-4］。共轨管压力是决定喷油压力和喷油量的关键因素［5］，在系统控制策略中对轨压的控制非常重要。轨压控制包括稳定控制和快速响应控制，稳定控制是指实际轨压稳定在目标值附近且瞬时波动量尽可能小；快速响应控制是指当发动机进行工况切换时轨压能快速达到目标值且超调量较小［6］。

柴油机采用的轨压控制模式为“前馈加反馈”，前馈控制是指通过转速和喷油量查询轨压MAP 的方式，反馈控制则是通过PID 控制器对轨压进行控制［7］。在反馈控制中，PID 控制器的参数决定着轨压控制效果，但PID 控制器参数整定需要花费许多资源和时间，且整定好的参数移植性较差。对于PID 参数整定，常用的方法有固定参数法［8］、神经网络法［9］、滑模变结构［10］、模糊控制法［11］等。在发动机实际运行过程中轨压是非线性时变的且有一定迟滞［12］，上述方法无法保证发动机在所有工况下的PID 参数均为最优。近些年，新型人工智能算法不断发展，获得广泛关注。在高压共轨系统控制优化方面，文献［13］中通过遗传算法对模糊PID 进行优化，实现对喷油量的灵活控制，但由于算法离散的操作，未能对结果进行有效验证；文献［14］中通过改进的遗传算法对共轨系统结构参数进行优化，降低了直喷汽油机共轨压力波动，但未考虑对超调量的控制；文献［15-16］中基于遗传算法和粒子群算法对传统轨压PID 控制器进行了改进，实现对轨压的优化控制，但为加快算法收敛速度而选择了较小的种群规模。海鸥算法是一种新型群智能算法，相较于遗传算法和粒子群算法，该算法在保证寻优精度的同时还有着结构简单的优势，可避免由于算法结构复杂难以应用到控制器中的问题，同时能获得较好的控制效果。与传统的工程手动整定PID 参数方法相比，使用海鸥算法自适应整定方法在使轨压更稳定、响应更快的同时，又避免了控制参数移植性差的问题，节省参数标定带来的人力、物力和时间成本的浪费，提高电控单元（electronic control unit，ECU）的开发效率。因此，提出一种基于改进海鸥算法的轨压PID 控制器参数整定方法，以实现优化柴油机工作性能的目的。根据柴油机高压共轨系统实际工作中非线性时变和滞后性的特点，结合混沌理论、非线性惯性权重和高斯-柯西变异策略优化后的海鸥算法，设计了在线自适应整定参数的轨压PID 控制器，并在MATLAB/Simulink 环境中通过仿真试验验证该方法的可行性和有效性。

1 高压共轨系统实时仿真模型开发

高压共轨系统主要由高压油泵、共轨管、喷油器及电控单元（electronic control unit，ECU）组成，结构组成如图1 所示。其工作原理主要是油箱中的燃油经低压油泵进入高压油泵，经过高压油泵加压后将其供入共轨管中储存，之后再定时定量供给喷油器进行喷油。在共轨管中，高压油泵的供油量和喷油器的喷油量会达到动态平衡状态，使得轨压稳定在一定范围内。

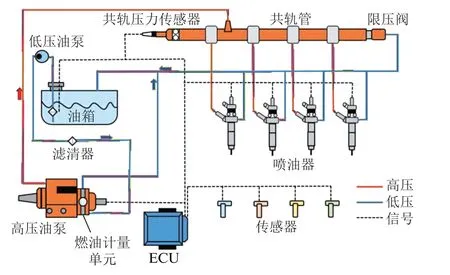
图1 高压共轨系统结构

为保证模型仿真的实时性，在对共轨系统进行建模时进行如下假设：（1）燃油在共轨系统中的流动为恒温过程；（2）整个共轨系统不存在燃油泄漏；（3）各管道不存在流动阻力；（4）各零部件不会产生弹性形变；（5）燃油一维非稳态流动；（6）各容腔压力处处相等，忽略燃油流动产生的压力传播时间。

1.1 燃油计量单元及高压油泵模型

燃油计量单元（fuel metering unit，FMU）安装在高压油泵的进油侧，通过ECU 控制电磁阀开度进而调节进入高压油泵柱塞腔的燃油体积。为兼顾模型仿真的实时性和准确性，FMU 的工作特性以MAP 形式给出，如式（1）所示。

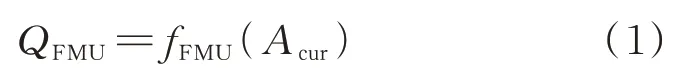
式中，QFMU为通过FMU 的燃油体积流量，mm3/s；Acur为当前电流值，mA。

通过FMU 的燃油进入柱塞腔，经偏心凸轮驱动柱塞加压形成高压燃油供入共轨管，凸轮轴每旋转1周发生3 次供油事件，其供油关系如图2 所示。

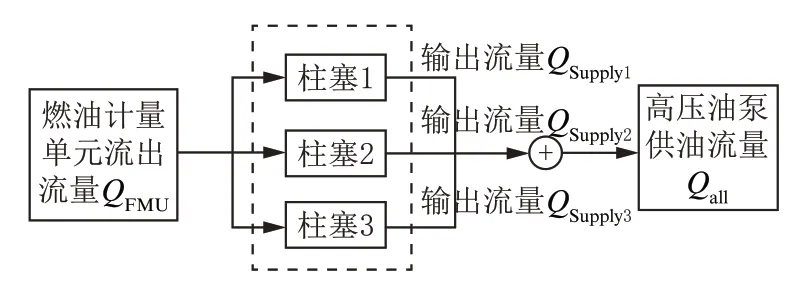
图2 高压油泵供油关系

高压油泵中3 个柱塞径向间隔120°分布，柱塞工作被划分为吸油和压油两个行程。高压油泵运行过程是相对复杂的，在模型计算过程中，可以忽略燃油在高压油泵中的工作过程，仅考虑高压油泵的输出供油流量［17］，以此来提高模型的计算速度。由于凸轮型线计算过程较为复杂，文中将凸轮型线计算简化为类正弦过程，模型中供油流量的大小由柱塞腔容积决定，忽略简化凸轮型线对高压油泵内部燃油工作过程的影响。图3 为简化后柱塞位移与凸轮轴相位关系图，将部分无有效柱塞升程凸轮相位归入吸油或压油行程。此时，柱塞吸油和压油行程均视为180°凸轮轴转角，3 个柱塞吸油会出现重叠过程。以柱塞3 为例，凸轮轴相位为0°≤φ＜60°和120°≤φ＜180°时柱塞1 和柱塞3、柱塞2 和柱塞3均处于吸油行程，供给柱塞3 的流量Qin1为QFMU的一半；凸轮轴相位为60°≤φ＜120°时，仅柱塞3 处于吸油行程，供给柱塞3 的流量为QFMU。

图3 柱塞位移与凸轮轴相位关系

当凸轮轴转角为180°时，柱塞进入压油行程，当柱塞压力大于轨道压力才会向轨道供油，否则不供油，图4 为单个柱塞的工作过程。图中，φ为凸轮轴相位。

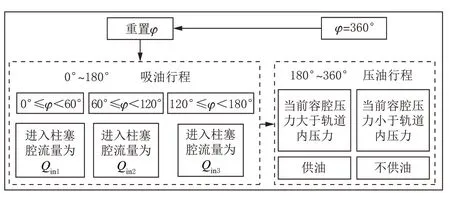
图4 柱塞工作过程

进入共轨管的燃油流量受柱塞腔体积的影响，柱塞腔体积随凸轮轴转角时刻变化，二者关系见式（2）。

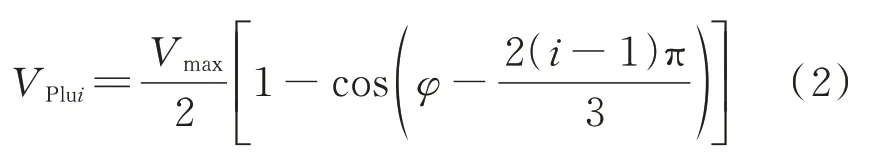
式中，VPlui为第i个柱塞腔瞬时容积，mm3，i=1，2，3；Vmax为柱塞腔最大容积，mm3。柱塞腔内压力由流体可压缩性方程计算得到，如式（3）所示。

式中，pPlui为第i个柱塞腔内瞬时压力，MPa；K为燃油体积模量，MPa；Qin为进入柱塞腔的燃油体积流量，mm3/s。燃油弹性模量与压力的关系见式（4）。

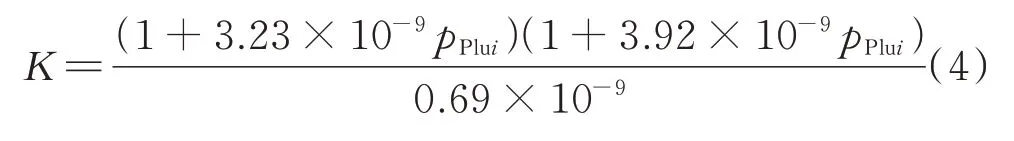
当柱塞开始供油时，进入共轨管内的燃油体积流量由伯努利方程计算得到，如式（5）所示。

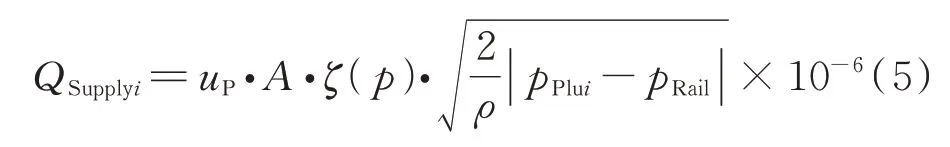
式中，QSupplyi为第i个柱塞的供油体积流量，mm3/s；uP为流量系数；A为柱塞腔到共轨管的有效流通面积，mm2；pRail为轨压，MPa；ζ(p) 为阶跃函数，当pPlui＞pRail时ζ(p)=1，否 则ζ(p)=0；ρ为燃油密度，kg/m3。ρ由经验公式计算得到，如式（6）所示。

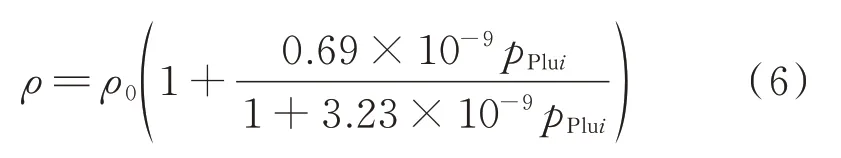
式中，ρ0为常压下燃油密度，0.853 g/cm3。进入共轨管内的总油量见式（7）。

1.2 共轨管模型

共轨管内压力主要受高压油泵供油量、喷油器喷油量及流向低压油道的燃油量扰动。轨压的计算公式见式（8）。

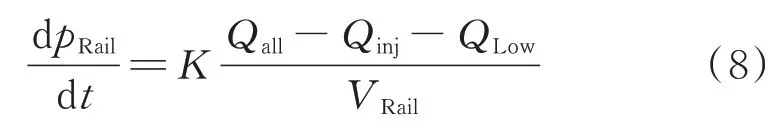
式中，Qinj和QLow分别为进入喷油器的燃油流量和共轨管流向低压油道的燃油流量，mm3/s；VRail为共轨管容积，mm3。

1.3 喷油器模型

该共轨系统共有4 个喷油器，喷油器的喷油速率主要由轨压、喷孔面积ANH、流量系数CD及喷孔两端压差决定，喷油速率计算公式见式（9）。

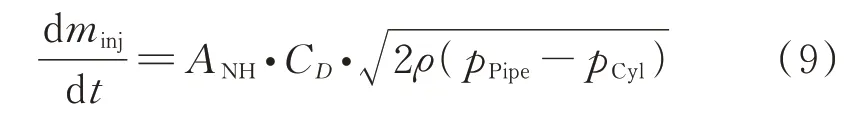
式中，minj为单位时间内喷油器喷出的燃油质量，mg；pPipe为高压油管 压 力，MPa；pCyl为 缸内压力，MPa。

1.4 模型实现及验证

以某型增压中冷4 缸柴油机高压共轨系统为建模对象，基于MATLAB/Simulink 软件环境搭建了燃油计量单元、高压油泵和共轨管等子模块，同时基于AVL/Cruise M 软件搭建了包含喷油器模型的目标柴油机模型。柴油机模型包含空气滤清器、增压器、中冷器及废气再循环系统等模型元件，高压共轨系统模型框架如图5 所示。

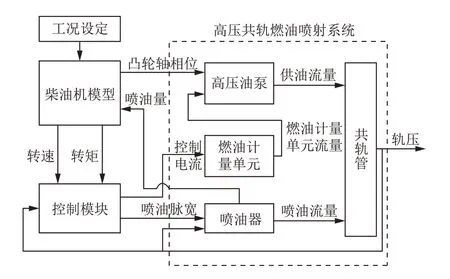
图5 高压共轨系统模型框架

在高压共轨系统中，喷油器对共轨管压力波动有着极大的影响，为了验证喷油器模型的准确性，需要对喷油器模型的喷油量进行验证。在AVL/Cruise M环境下，将喷油器模式设置为轨压进入模式，将模型的仿真数据与台架试验数据进行对比，验证了喷油器在不同轨压和喷油脉宽下的喷油量，结果如图6所示。每循环喷油量最大误差均小于5%，证明该喷油器模型可用于后续高压共轨系统模型集成测试。

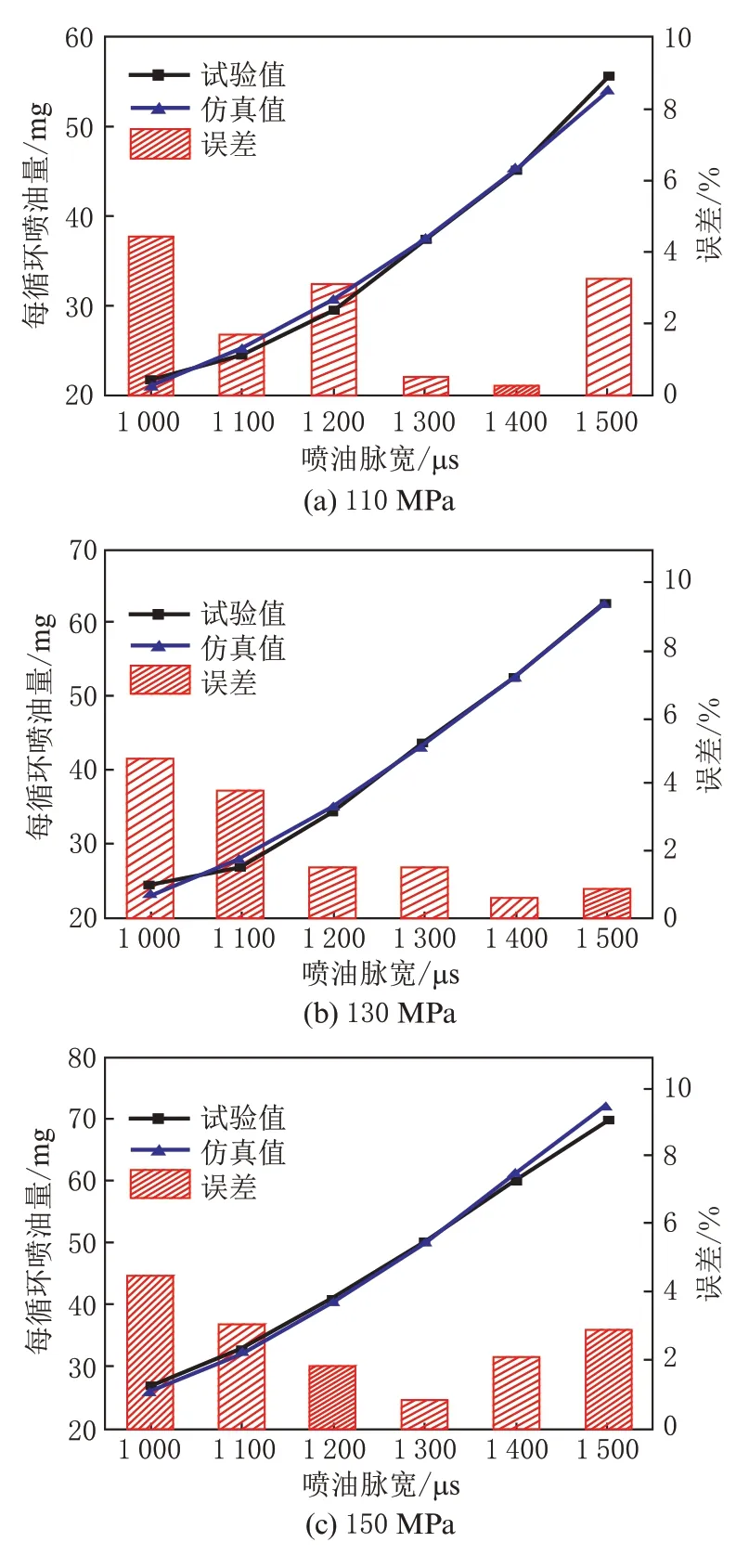
图6 不同轨压和喷油脉宽下喷油准确性验证

将柴油机模型在AVL/Cruise M 环境下编译生成DLL（动态链接库）文件，在Simulink 环境中与其他子模型整合成完整的柴油机及高压共轨系统模型。在不同转速下，高负荷时发动机供油量和喷油量较大，对轨压扰动较为显著，因此选取发动机最大转矩工况点（1 600 r/min、100% 负荷）和高转速工况点（2 800 r/min、100% 负荷）对模型进行验证，将仿真结果与台架试验数据进行对比，结果如图7 所示。仿真数据与试验数据较为符合，误差在5% 以内，具体数据如表1 所示。据此可认为所建立的高压共轨系统模型能够较好地模拟共轨管的轨压波动情况，可用于检验算法的控制效果。

表1 共轨压力波动数据

图7 高压共轨系统模型轨压波动验证

2 海鸥算法基本原理及改进措施

2.1 基本海鸥算法

海鸥是一种具有高智慧的群居鸟类，它们会随着季节的变化进行迁徙和觅食。在迁徙时，海鸥按照一定规律保持个体飞行并避免相互碰撞；在捕食时，海鸥以螺旋轨迹飞向猎物并发起攻击。根据海鸥的迁徙和捕食规律，Gaurav Dhiman 教授于2019年提出了一种新型群智能算法——海鸥算法（seagull optimization algorithm，SOA），该算法原理简单，具有较高的搜索精度和收敛速度［18］。

2.1.1 迁徙（全局搜索）

在迁徙途中，为了避免发生碰撞，采用A 来计算海鸥的个体更新位置，如式（10）、式（11）所示。

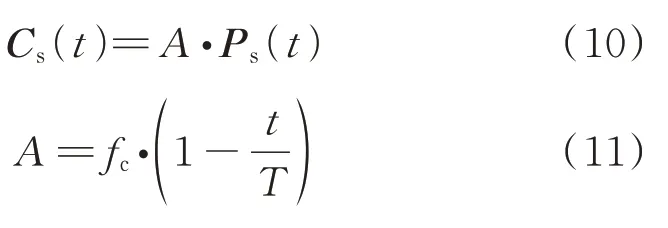
式中，Cs(t) 为不与其他个体发生干涉的新位置；Ps(t)为当前海鸥位置；t 为当前迭代次数；A 为海鸥在解空间中的动态过程描述；fc为控制因子，一般设为2；T 为最大迭代次数。海鸥避免与其他个体发生碰撞，会朝着最优位置移动，最优个体位置方向计算公式见式（12）。

式中，Ms(t)为最优个体位置的相对方向；Pbs(t)为最优个体位置；B 为负责平衡全局搜索和局部搜索的变量；R 为［0，1］内的随机数。海鸥朝着最优位置移动，最终会到达一个新的位置，海鸥与最优位置之间的距离Ds(t)如式（14）所示。

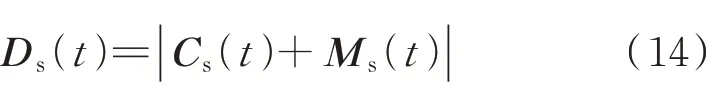
2.1.2 攻击（局部搜索）

海鸥在空中进行螺旋运动，通过不断变换速度和角度攻击猎物，其运动轨迹如式（15）所示。

式中，r 为螺旋半径；θ 为［0，2π］内的随机数；u 和v为螺旋形状相关常数。海鸥的攻击位置见式（16）。

2.2 改进海鸥算法

海鸥算法结构简单，有着较好的寻优能力，但也存在一定的缺陷，例如算法收敛过早、容易陷入局部最优等［19］，这会导致在寻优过程中无法得到轨压PID 控制器参数的最优组合。为此，提出了一种基于高斯-柯西变异的混沌海鸥算法，在一定程度上更好地平衡算法的全局搜索和局部搜索能力，避免算法早熟，加快后期收敛速度。

2.2.1 Tent 混沌映射种群初始化

海鸥算法在初始化种群的时候是完全随机的，初始种群在搜索空间上的分布具有不确定性，当初始种群分布不均匀时，会导致算法早熟或陷入局部最优。混沌映射由于具有遍历性、随机性和整体稳定性等优点被广泛应用于优化领域。混沌映射能代替随机数生成器生成混沌序列，对种群进行初始化，且往往能取得较好的效果。

Tent 映射又称帐篷映射，是最常见的混沌映射之一，具有均匀的分布函数和良好的相关性，可以在种群初始化的时候生成分布均匀的种群，其表达式见式（17）。

式中，xk为第k次迭代的混沌值；a为常量，文中设为0.4。将Tent 映射迭代1 000 次的取值分布与普通随机取值进行对比，如图8 所示。相比之下，混沌映射的取值分布更加均匀，更适用于算法种群初始化。

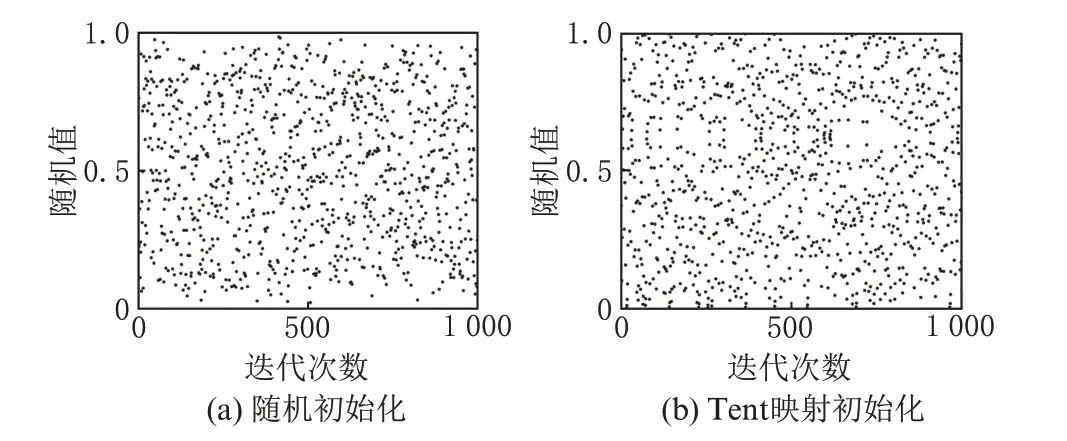
图8 初始化取值分布图

2.2.2 非线性收敛因子和自适应权重

收敛因子A在算法计算过程中是线性下降的，而算法的收敛过程是非线性化的，因此线性下降的A并不能与算法的整个搜索过程相契合。为此引入激活函数中的tanh 函数（双曲正切函数）将收敛因子A非线性化。tanh（x）的表达式见式（18）。

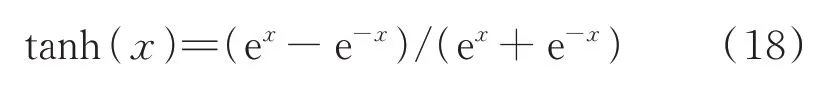
选取tanh（x）函数在［-3，3］区间上的图像，对图像依次进行伸缩、对称和平移等操作，将A的迭代式代入其中得到改进后的公式，见式（19）。

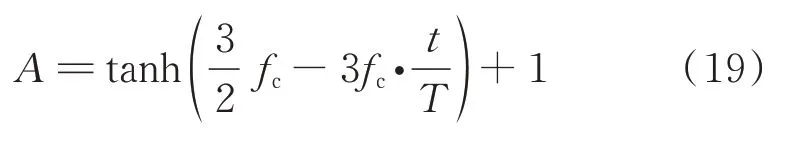
图9 为改进前后A的图像对比。由图9 可知，在迭代前期A的值较大且下降速度缓慢，有利于增大海鸥的搜索范围，提高算法的全局搜索能力；在迭代中期A快速下降有利于加速算法收敛；在迭代后期A的值较小且变化缓慢，有利于加强算法在局部范围内的搜索能力。

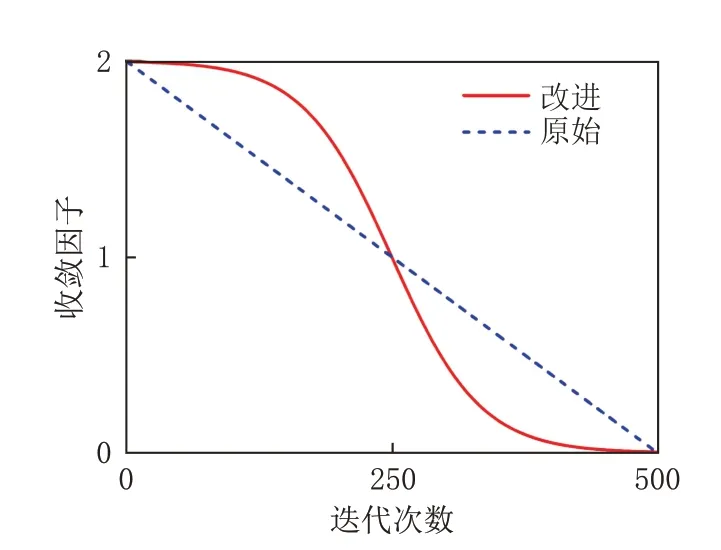
图9 收敛因子改进前后对比

引入自适应惯性权重更加符合算法的寻优机制，增强算法后期寻优能力，避免海鸥陷入局部最优。惯性权重公式见式（20）。

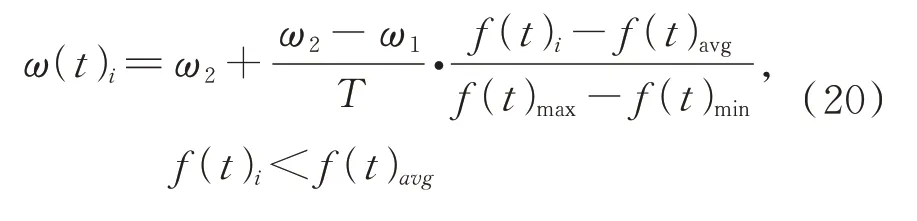
式中，ω(t)i为第i个代理在第t次搜索的权重；ω1、ω2为初始最小和最大权重；f(t)i为第i个代理在第t次 搜索 的适应度值；f(t)avg、f(t)max、f(t)min分别为第t次迭代种群适应度的平均值、最大值和最小值。

2.2.3 高斯-柯西变异策略

柯西变异和高斯变异能提升算法的优化性能，其中，柯西变异可以提高种群多样性，加速海鸥朝着全局最优解移动；高斯变异可以增强算法的局部搜索能力，避免陷入局部最优的困境，增强算法跳出局部最优的能力。变异公式见式（21）和式（22）。

式中，Pgs(t)、Pcs(t) 分别为高斯变异和柯西变异后的海鸥位置；RGau为高斯随机数；RCau为柯西随机数。为判断何时开始局部搜索，需要引入海鸥的历史最优适应度变化率。开始进行局部搜索的条件是变化率连续n代小于阈值α，判断公式见式（23）。

式中，f(Ps(t))为最优海鸥适应度。阈值α的取值十分关键，阈值过大会使得算法无法充分对解空间进行搜索，陷入局部最优；阈值过小会使得海鸥集中在历史最优解附近，无法找到全局最优。文献［20］中指出当阈值为0.000 1 时能有效判断算法是否进行高斯变异。

2.3 算法优化结果分析

为验证改进后的海鸥算法（improved seagull optimization algorithm，ISOA）的有效性，选取25 个具有不同特征的测试函数对SOA 和ISOA 进行测试。此处由于篇幅限制，从其中分别选择3 个单峰测试函数和3 个多峰测试函数的结果进行分析，如表2 所示。F1～F3 为单峰测试函数，单峰测试函数可以有效检验算法的全局搜索能力；F4～F6 为多峰测试函数，多峰测试函数可以对算法的收敛速度和精度进行有效检验。

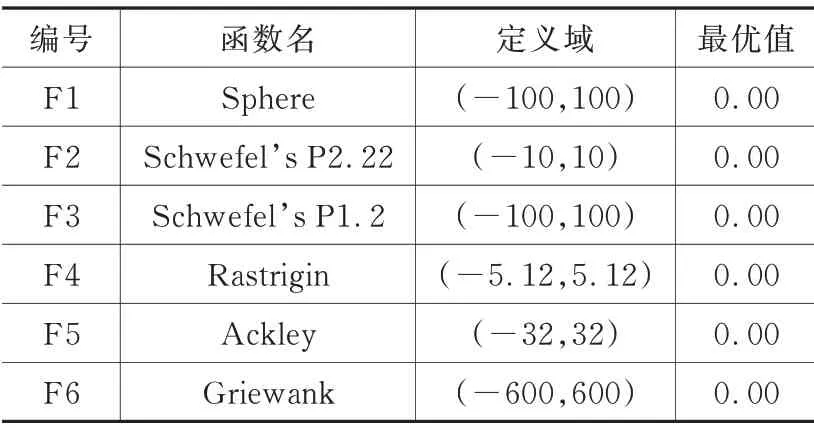
表2 选用的6 个测试函数

在进行测试时，算法种群规模均设置为50，最大迭代次数为100，函数测试维度d设置2、30 和60共3 组。为避免算法随机性带来的影响，两种算法在每一个限制条件下各运行15 次，剔除最好和最坏的结果后得到的平均值则为各测试函数下适应度值的最优值，结果如表3 所示。

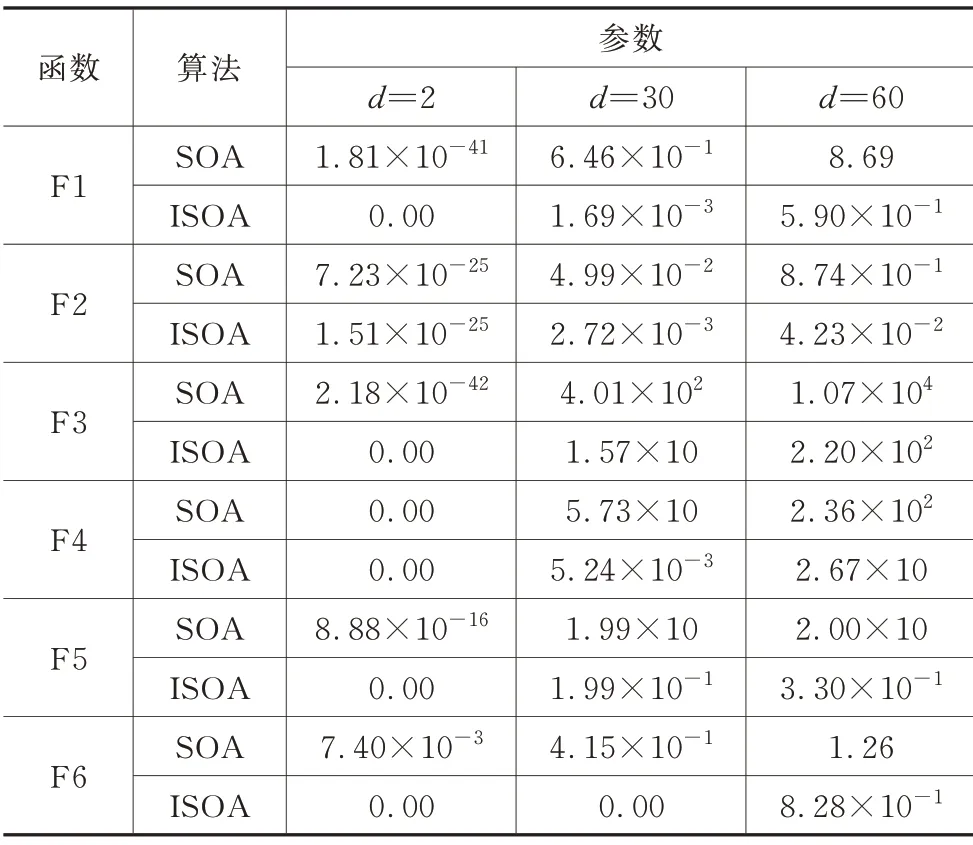
表3 测试函数优化结果

从表中可以看出，相比SOA，ISOA 的计算结果更接近理论最优值，说明ISOA 寻优精度更高，且算法在一定程度上具备跳出局部最优的能力。

图10 为改进前后算法对6 个测试函数在30维度下求解最优值的收敛曲线对比。从图中可以看出，ISOA 的收敛曲线下降更快，以较小的迭代次数收敛到最优值，且计算值更接近于理论最优值。ISOA 较SOA 有更快的收敛速度和更高的收敛精度，同时解决了SOA 在部分情况下不收敛的问题。

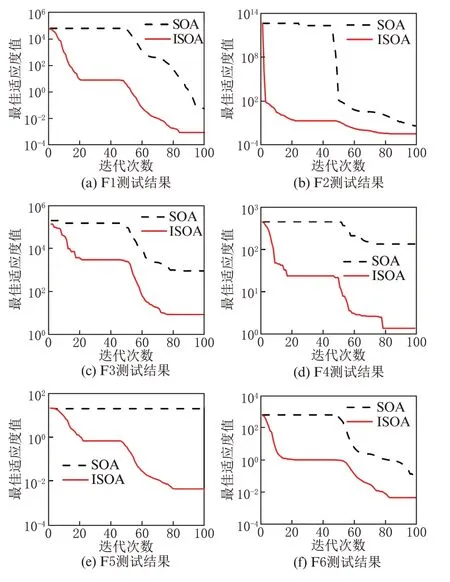
图10 SOA 和ISOA 算法收敛速度对比

3 高压共轨系统轨压控制仿真分析

3.1 轨压控制优化及参数自整定过程

在发动机实际工作过程中，共轨压力主要受喷油量和供油量两个因素影响，轨压保持稳定的条件是喷油量和供油量处于动态平衡过程。喷油量是由喷油控制策略决定的，本研究中主要讨论如何优化供油量来优化轨压的稳态特性和动态特性。在轨压控制策略中，轨压的PID 控制是一个重要环节。ECU 根据发动机当前工况确定轨压目标值，通过与来自轨压传感器的实际轨压计算偏差。轨压偏差进入PID 控制器后计算得到控制电流大小，经过信号转换后，最终由高压油泵将燃油供入共轨管，对轨压进行调节。

发动机的许多控制过程是以轨压稳定控制为前提，其稳定性和快速响应性是柴油机诸多性能的影响因素［21］。由于高压共轨系统在实际运行过程中是非线性时变的，根据轨压的连续变化不断调整供油量更加符合共轨系统的运行特点。因此，在原有控制策略的基础上，通过ISOA 算法根据轨压偏差在线自适应寻优PID 控制器的参数，替代MAP 查询参数的方式来优化轨压控制过程，动态调整供油量的大小，尽可能地平衡喷油事件对轨压的影响，使得稳定工况下轨压波动尽可能小。同时，在动态工况下，将超调量和轨压稳定时间作为优化目标，通过优化PID 参数减小超调量和缩短稳定时间。优化轨压PID 控制过程可减小轨压波动对喷油及其他控制过程造成的影响，最终实现优化发动机性能的目的。图11 为ISOA 算法的PID 控制原理图。在寻优过程中，将比例参数Kp、积分参数Ki和微分参数Kd这3 个参数定义为解空间中的一个坐标点，海鸥个体在解空间中的坐标代表PID 参数的一个组合［Kp，Ki，Kd］，且在这个空间中存在一个点使得轨压的控制效果最好。图12 为参数整定计算流程图，具体步骤如下：（1）参数初始化。种群数量设为50，最大迭代次数设为100，利用混沌映射生成初始海鸥种群。（2）适应度值计算。在控制过程中，优化的目标是在稳定工况下轨压波动量尽可能小，在工况切换时稳定时间尽可能短且超调量较小。适应度函数表达式见式（24）。

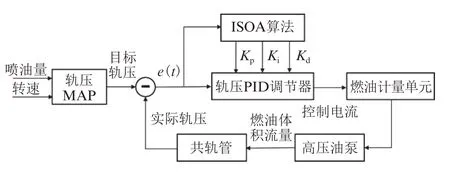
图11 ISOA 算法的轨压PID 控制原理图

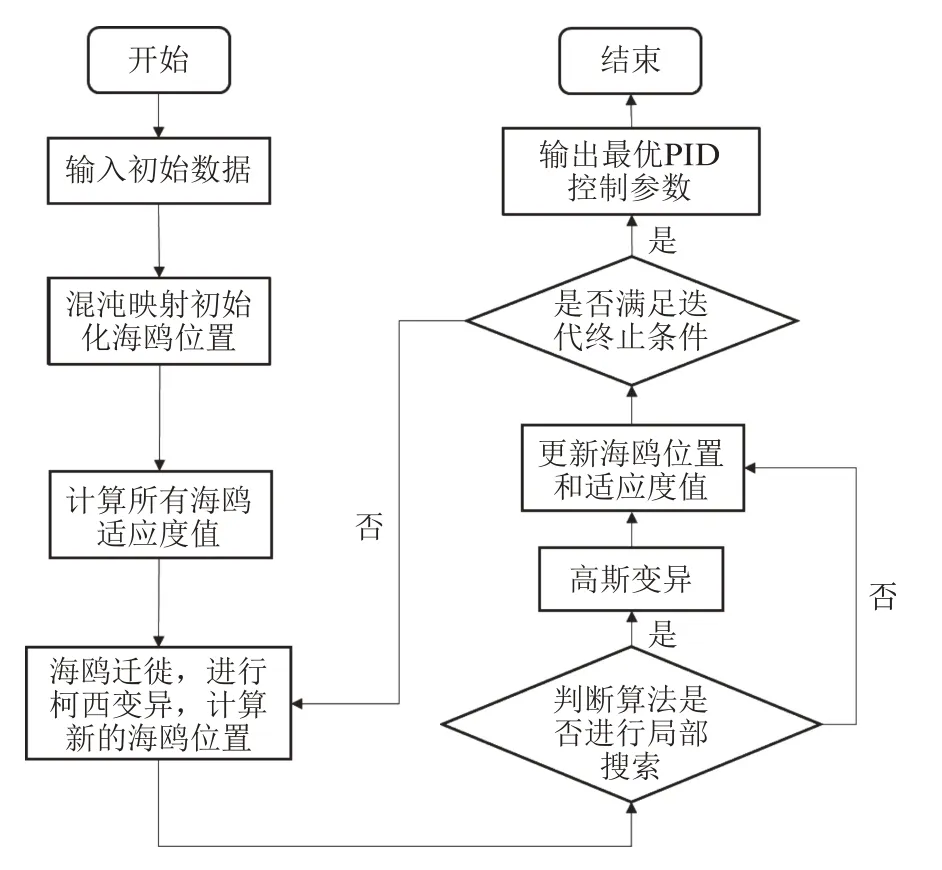
图12 自适应PID 轨压控制算法流程图

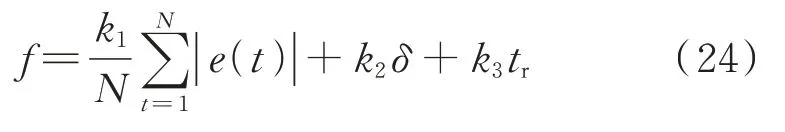
式中，e(t)为瞬时轨压偏差；δ为超调量；tr为稳定时间；N为采样点个数；ki为加权系数。将海鸥位置代入式（24）得到适应度值，并确定最优海鸥位置。（3）海鸥迁徙。按照式（10）～式（14）控制海鸥进行迁徙，并进行柯西变异。（4）更新海鸥位置，计算当前海鸥适应度值，若当前个体适应度值优于历史个体最优适应度值则将其更新，否则不更新。（5）根据式（23）判断是否进行局部搜索，若是则按照式（15）、式（16）计算海鸥攻击位置，并进行高斯变异，否则进入下一步。（6）计算所有海鸥的适应度值并更新全局最优个体位置。（7）判断是否达到最大迭代次数，若是则输出最优解，否则跳转到步骤（3）继续搜索。

3.2 轨压稳定工况仿真测试

在MATLAB/Simulink 环境下，将算法程序与上述搭建的柴油机及高压共轨系统模型集成进行仿真测试。为了验证算法的可行性和有效性，将工程整定方法和粒子群算法（particle swarm optimization，PSO）与ISOA 进行比较。

为验证算法在不同轨压下的控制效果，将发动机负荷设定在30%，转速分别为1 200 r/min、2 000 r/min 和2 800 r/min 时分析ISOA、PSO 优化后的PID 和工程整定增量式PID 对稳定工况下轨压的波动抑制效果，结果如图13 所示。其中，工程整定下的轨压波动曲线通过标定软件INCA 实时采样真实台架轨压数据绘制而成。由图13 可以看出，工程整定方法下的轨压虽然能稳定在目标轨压附近，但是局部会出现轨压突变或周期性震荡。PSO 和ISOA优化后的轨压均能更好稳定在目标值附近，且未出现较大轨压波动，其中ISOA 优化后的轨压波动明显更小。

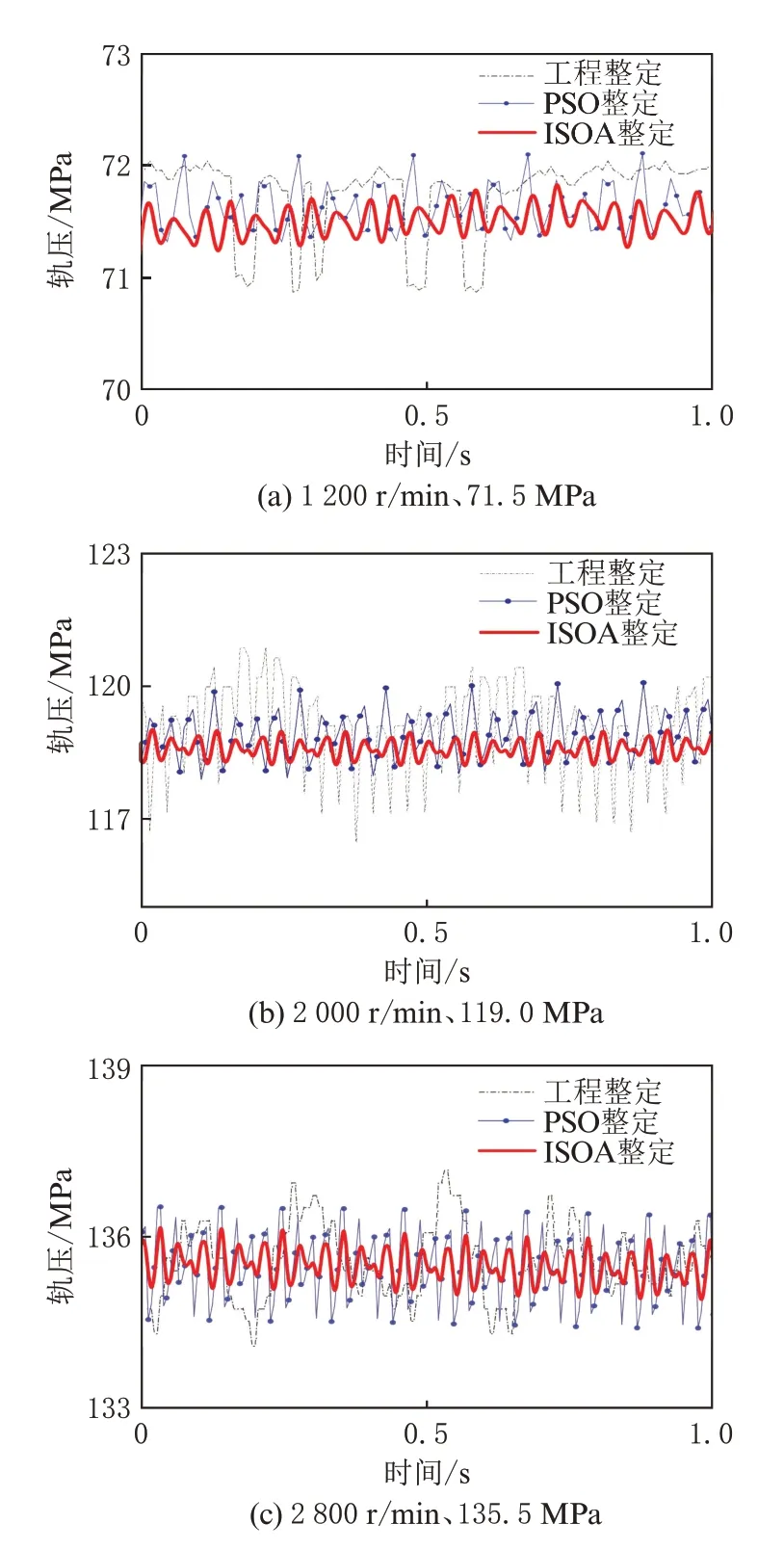
图13 不同稳定工况下3 种整定方法轨压波动对比

表4～表6 为3 种工况下轨压波动的具体数据。在3 种稳定工况下，PSO 和ISOA 优化控制的轨压波动幅值和方差均小于工程整定方法，且ISOA 控制的轨压波动更小更稳定。相比于工程整定方法和PSO，ISOA 优化后的轨压波动幅值分别减少33%和16% 以上。

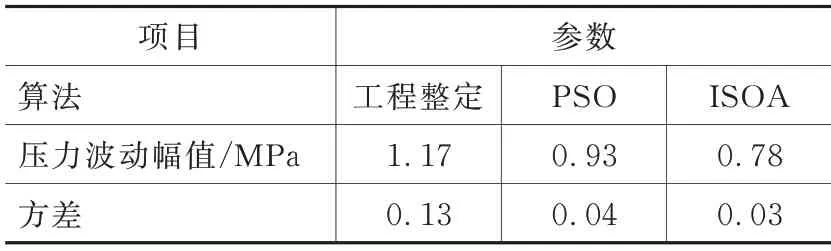
表4 1 200 r/min、71.5 MPa 下轨压波动数据

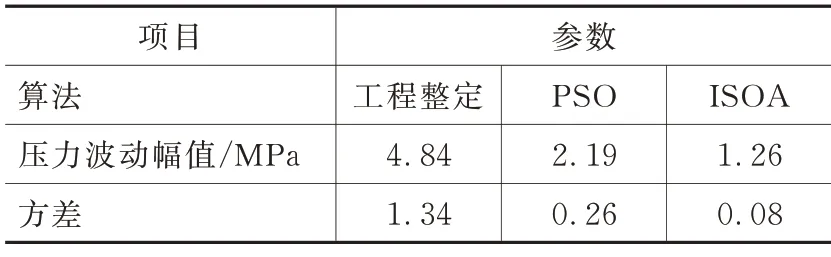
表5 2 000 r/min、119.0 MPa 下轨压波动数据

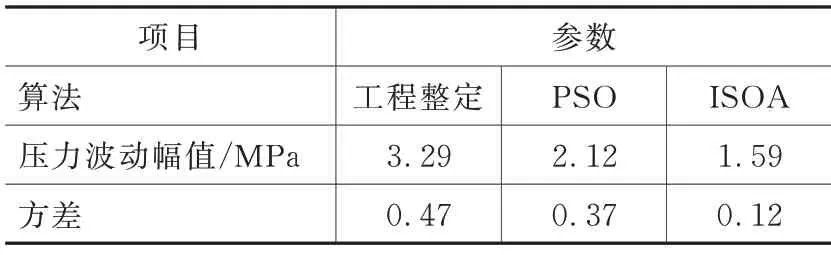
表6 2 800 r/min、135.5 MPa 下轨压波动数据

3.3 轨压变化工况仿真测试

在对轨压控制效果检验时，不仅需要分析稳定工况下轨压的波动情况，同时也需要考虑工况切换时控制方法对轨压的稳定时间和超调量的影响。

为此，将发动机转速稳定在2 000 r/min，负荷从60% 升高至90%，待转速稳定一段时间后再将负荷降低至60%，分析了该过程中3 种方法优化后的轨压变化情况。为了便于观察轨压的变化情况，此处将轨压变化曲线进行滤波处理，结果如图14 所示。

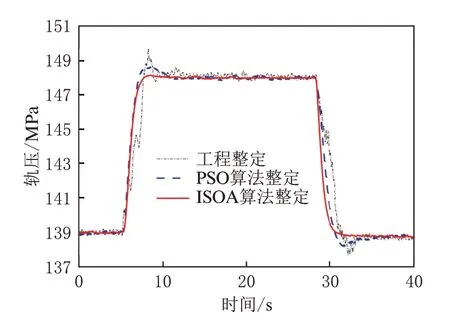
图14 负荷升降时轨压变化情况（60%负荷～90%负荷）

在图14 中，当发动机负荷变化时，PSO 和ISOA控制下的轨压能快速响应达到目标轨压并保持稳定。当负荷升高时，ISOA 的轨压响应速度和PSO 基本相同但超调量更小，相比于工程整定方法和PSO，稳定时间分别缩短0.50 s 和1.27 s，超调量分别减小了1.59 MPa 和0.48 MPa。当负荷降低时，ISOA 控制下的轨压几乎未出现超调量。相比于工程整定方法和PSO，稳定时间分别缩短0.92 s 和0.81 s，超调量分别减小了1.13 MPa 和0.55 MPa。

当发动机加、减速的时候，轨压会随之改变。为此，将发动机转矩设定为200 N·m，分析了工程整定方法、PSO 和ISOA 算法控制下，发动机转速从1 000 r/min 升高到1 400 r/min，待转速稳定后再降低至1 000 r/min 时的轨压变化情况，将轨压变化曲线进行滤波处理，结果如图15 所示。

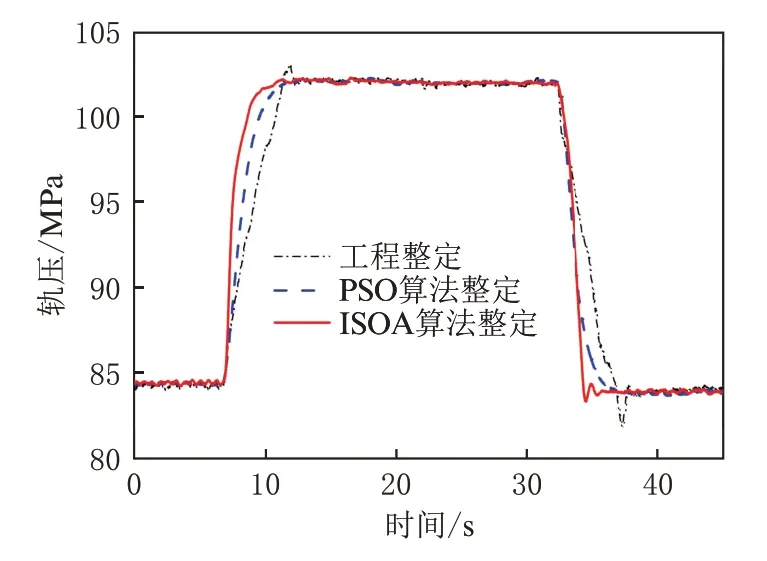
图15 加、减速时轨压变化情况（1 000 r/min～1 400 r/min）

当转速变化时，ISOA 控制下的轨压能在较短时间内达到目标轨压并保持稳定。在转速升高时，相比于工程整定方法和PSO，稳定时间分别缩短0.60 s 和0.34 s，超调量分别减小了0.95 MPa 和0.05 MPa。在转速降低时，相比于工程整定方法和PSO，稳定时间分别缩短1.69 s 和0.84 s，超调量分别减小了1.45 MPa和-0.43 MPa。此时尽管ISOA 控制下轨压超调量大于PSO 方法，但稳定时间较PSO 更短。

4 结论

（1）针对算法的寻优精度和收敛速度，使用不同测试函数对改进前后的海鸥优化算法进行测试，结果表明：改进后的算法在寻优精度和收敛速度等方面有了较大提升，且具备一定的跳出局部最优的能力。

（2）采用改进的海鸥优化算法对控制参数在线寻优后减小了轨压的稳态波动量，同时在动态控制过程中缩减了轨压的稳定时间和超调量。在3 种稳定工况下，相比于工程整定方法和PSO，ISOA 优化后的轨压波动幅值分别减小33% 和16% 以上；在动态过程中，稳定时间分别缩短14% 和8% 以上，超调量分别减小了71% 和20% 以上。ISOA 有较高的计算精度和更快的收敛速度，在轨压稳定控制和快速响应控制方面有明显的优势及可行性，具有较好的工程意义。