基于Campbell理论的航空发动机涡轮叶片共振裕度分析
2022-10-19田森吴娅辉贾志婷张大治谢兴娟姜延欢
田森,吴娅辉,贾志婷,张大治,谢兴娟,姜延欢
(航空工业北京长城计量测试技术研究所,北京 100095)
0 引言
航空发动机是最复杂的、多学科集成的工程机械系统之一,涉及空气动力学、工程热力学、燃烧学、结构强度、控制技术、试验与测试技术、材料学和制造工艺等众多学科及技术领域。由于航空发动机的服役环境较恶劣,在实际运行过程中会承受不同类型的交变载荷[1],整体的失效问题会被逐渐放大。而作为航空发动机的核心组成部件之一的涡轮叶片,其运动工况除了要承受高速旋转产生的离心载荷、实际飞行条件下高温高压气流非均衡变化产生的气动载荷、复杂环境无规律变化导致的温度载荷外,还要承受强迫振动及涡轮叶片本身自激振引起的共振、喘振及颤振等载荷。近些年来,随着发动机故障问题的频繁出现,据相关材料统计分析,因发动机振动失效引起的事件约占发动机总失效事件的60%,因叶片振动导致的失效事件则占总振动失效事件的70%之多[2],叶片振动导致的疲劳损伤和断裂已成为航空发动机失效工况中最为严重的问题。
目前国内航空发动机热端部件设计技术与国际先进水平仍有较大差距,尤其是涡轮叶片等重要零部件受振动影响的工作寿命远低于发动机实际要求,现已成为航空发动机技术发展所面临的瓶颈难题。因此迫切需要从叶片的固有振动与动力学响应特性等角度出发进行深入研究和分析,避免共振频率等现象的出现。为发动机涡轮叶片的设计、性能评估和故障诊断提供可靠的理论支撑[3]。
本文将非接触模态试验测量法与半物理场仿真计算法相结合,同步完成对叶片振动特性的分析[4]。基于模态分析基本理论确定发动机涡轮叶片的振动特性,采用模态试验中自激励锤击法与ANSYS软件求解的结果进行横向对比,以验证求解方法的可靠性以及叶片仿真建模的合理性。整合该涡轮叶片在各工况下固有频率和模态振型的结果,绘制出不同转速下的Campbell图[5],基于共振裕度理论计算,给出容易发生危险的工作转速及对应工况,并提出相应改进措施。对发动机涡轮叶片的振动故障分析和性能评价具有较强的指导意义。
1 模态分析基本理论
对涡轮叶片进行模态分析主要是为了获得该转子的振动特性,其振动模态为转子系统结构所固有的属性[6],叶片模态分析主要包括叶片本身固有频率的计算和每阶对应振型的归类。本文主要借助模态分析的基本理论确定涡轮叶片的振动特性。
1.1 模态分析基本原理
本文所研究的是某型号航空发动机涡轮叶片,其本质是一个连续变化的多曲面复杂结构,常规计算方法无法得到一个准确的结果。因此,需要经离散化处理计算将其变成一个符合实际工况条件下的多自由度系统。依据有限元弹性力学理论方法,该多自由度线性弹性系统的基本运动微分方程公式为[7]

式中:[M]为多自由度线性弹性系统的质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵;为加速度响应;为速度响应;X(t)为位移响应;F(t)为动态激励载荷。
通常情况下,模态分析的理论计算均采用无阻尼自由振动法来进行求解。此情况下,式(1)中的[C]{},{F(t)}默认为0。因此可将涡轮叶片转子系统的模态分析问题转化为求解特征值与特征向量问题,为
求解可得
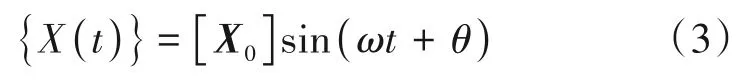
式中:ω为多自由度系统的固有频率值;[X0]为振幅矩阵,即n维n列。将式(2)和式(3)进行整理,得

特别注意,当该系统进行自由振动时,振幅矩阵为有效值,依据克莱默法则可以计算得到

由于式(4)和式(5)中的X0和ω2的求解问题是一个求解广义特征值的问题,则这n个特征向量分别满足

从上述分析结果可以看出,模态分析的整个计算过程实质为一种不同空间类型条件下的坐标变换。因传统的模型计算是在物理坐标条件下,无法与模态坐标点数值相对应,所以要将建立好的方程组联立求解,最终确定出该弹性系统的模态参数。其中,联立方程组中待求解的矩阵为模态矩阵,矩阵中每列的参数信息代表该解算对象的模态振型,模态振型所对应的具体变形大小并无实际意义,只是相对振型的变化量,与结构仿真的变形有所区分。因此一般情况下,一个完整的多自由度弹性振动系统其自由度个数、固有频率个数和固有主振型个数均为相等。
2 涡轮叶片的ANSYS模态分析
ANSYS有限元分析利用数学近似的方法对真实物理系统(结构和载荷)进行结构模拟。本文的仿真计算分析对象是某型号航空发动机涡轮叶片,采用实体建模分析法,完成对叶片的结构建模,随后基于ANSYS-Modal模块环境,完成对叶片固有振动特性的分析与计算。
2.1 实体建模
航空发动机涡轮叶片是一个多曲面复杂结构,其建模的难点在于其外轮廓剖面曲率大、叶身整体厚度宽,并在叶高方向存在明显的变化趋势。解决这些问题正是航空发动机涡轮叶片建模的关键点。从另外一种角度分析涡轮叶片的实质为较多复杂曲面叠加的结果,所以在建立几何模型时,采用实体建模法完成。完整的叶片结构是由叶盆、叶背及榫头几部分组成,如图1所示。

图1 结构模型Fig.1 Structural model
因涡轮系统本身质量较大、工作环境温度较高,所承受的交变载荷较复杂,在叶片设计制造时优先选用镍基高温合金材料,其良好的力学性能和抗氧化指标可满足试验测试需求。叶片材料的力学性能参数如表1所示[8],其中线膨胀系数及热导率都会随着温度的升高而变大,在900℃左右时,线膨胀系数达到15.48×10-6,热导率达到25.24 W/(m·℃)。

表1 涡轮叶片材料的力学性能参数Tab.1 Mechanical property parameters of turbine blade materials
2.2 模型计算
有限元几何模型网格划分方法通常分为自由网格划分法和映射网格划分法。其中映射网格划分法适用于规则图形,故采用自由网格划分法。叶片的榫头部分采用四面体二阶单元,叶身的部分采用六面体单元,叶身的网格划分精度和密度较高,可满足后期试验对叶身振动特性的分析。考虑到叶片榫槽及进排气孔承受较大的载荷和变形,模型的单元数量应确保具有67993个。虽然整体采用自由网格划分方法[21],但是使用了Solid 186带中间节点的六面体三维实体单元,弥补了因自由网格划分的不足与缺陷。有限元网格划分模型如图2所示。

图2 网格划分Fig.2 Meshing
除完成涡轮叶片的网格划分外,还需根据实际工况对叶片施加边界约束条件[22]。通常情况下,在ANSYS-Modal中约束条件的施加方法分为两种:第一种是在模型的关键点、线和面上施加约束条件;第二种是在单元和有效节点上施加约束条件。通常对于多基准面叠加的结构模型,为了避免由于网格大小的改变而造成边界条件施加位置、精度、以及方式的变化,一般采用第一种方法。为了更加符合涡轮工作叶片的实际工作状态,边界条件上的具体约束施加位置为该涡轮叶片底端面上节点的法向全位移约束[9],如图3所示。

图3 计算边界条件Fig.3 Calculating boundary conditions
2.3 结果分析
结合实际工况具体分析,一般情况下,在叶片的各阶振型中,低阶固有振型对叶片的影响高于高阶固有振型,频率越高,振幅越小,危险性也越小。模态分析产生的振形数值并非实际意义的值[10],仅表示方程的特征解,还需要从叶片的振型与固有频率两方面进行深入分析。因此选取叶片振动特性的前6阶进行分析,各阶振动模态分析结果如图4所示。
从图4可以看出,叶片的第1阶振型为1阶周向弯曲振动,固有频率值为863.69 Hz;第2阶振型为1阶轴向弯曲振动,固有频率值为3100 Hz;第3至第6阶分别表现为1阶的扭转振动、1阶的二次轴向弯曲扭转振动、1阶的二次扭转振动、1阶的二次周向扭转弯曲振动,固有频率值分别为4008.1,4738.1,5925.2,6558.9 Hz。依据叶片振型的变化趋势,可以看出涡轮叶片的尖端和前缘侧壁处会存在较大变形,会在发动机工作区域内部形成不稳定的气流流场,从而降低实际的工作效率,严重的会引发涡轮叶片发生颤振和疲劳损伤的现象[11]。

图4 叶片1~6阶振型图Fig.4 Modal shapes of blade in order 1~6
考虑不同工况下涡轮叶片的工作转速也不相同,离心力对叶片的固有频率也会造成一定的影响,主要是因为涡轮叶片在离心载荷的作用下,会承受一个初始载荷场,随转速的间隙性变化,叶片的固有频率及刚度会发生不同程度的改变。为此,选择发动机在静止、滑行、进场、慢车、爬升、起飞六个状态[13-14]即对应不同转速情况下固有频率的变化趋势进行后续分析,如表2所示。

表2 不同工况下涡轮叶片固有频率Tab.2 Natural frequency of turbine blade under different working conditions
3 涡轮叶片的试验模态分析
模态分析试验的最终目的是获取被测目标的模态参数,包括输入和输出的信号处理、传递函数模型的解算分析、模态参数特征的有效识别等。因此,对涡轮叶片开展模态分析试验,可以确定该叶片的实际振动频率、振型等振动特性参数。本文通过试验自激励锤击法对叶片进行模态分析,将测量结果与有限元仿真分析结果进行对比验证,确定模型构建的合理性与实用性[12]。
3.1 硬件搭建
模态试验分析以某型号航空发动机涡轮叶片作为研究对象,试验硬件测试系统主要包括德国NV公司的自激励锤、Polytec公司的PSV-500激光测振仪、数采机箱、数据处理等部分组成,如图5所示。该试验系统中叶片的固定夹具是根据实际尺寸自行设计加工。

图5 模态分析试验系统Fig.5 Modal analysis test system
本文所提到的模态分析试验有别于传统的试验手段及解算过程。传统的试验手段是在叶片表面的特定坐标布置压电式加速度传感器,通过采集该传感器的响应信号与激励信号,两者做模/数转换,完成对应信号分析,对叶片的规格尺寸、传感器的选型及布置方式提出较高要求。而激光测振仪则可以很好地规避这些问题,通过提取叶片表面的振幅和频率完成对应信号的分析与解算,可满足远距离、高空间分辨力、响应频带宽、被测研究对象结构复杂等特点的场合。
3.2 试验过程
为了模拟叶片的实际工作状态,将其固定在实验台上,通过图像识别手段,将多曲面叶片的投影传输到数据处理模块中,并在叶片表面建立了135个测量点,按照单侧从上到下依次排列,如图6所示。按顺序,将第1测量点既作为模态试验的响应信号输出点也作为本次试验的激励点之一,剩余测量点同为激励点。将试验中自激励锤信号作为激励信号与采集设备Ⅰ号通道相连接,激光干涉仪采集到的信号作为响应信号与采集设备Ⅱ号通道相连接。用力锤依次敲击135个测量点,确保每个测量点都能被连续敲击3次以上,测量系统会自动计算每个测量点的平均响应函数,并分别与涡轮叶片实体模型中的有效节点相对应,最后利用动态信号分析软件获取叶片前6阶的振动频率与振型。

图6 模型测试点分布Fig.6 Model test point distribution
3.3 试验结果
按上述方法对某型号航空发动机涡轮叶片进行振动模态试验,分析后得到前6阶的模态振型结果如图7所示,叶片每阶的固有频率参数如表3所示。

图7 1~6阶振型试验结果Fig.7 Test results of 1~6 mode shape
表3 叶片1~6阶固有频率Tab.3 Modal natural frequencies of blade in order 1~6
将模态试验测量结果与无转速条件下ANSYS模态仿真分析结果进行对比验证,如图8所示。固有频率的数值随着模态阶数的增大而增大,试验数值与总体的变化趋势与仿真建模的处理结果相接近[15]。虽然模态试验法获得的每阶固有频率值略高于仿真结果,主要是由于试验环境条件、设备的测量误差以及所建立的计算模型与实际叶片的差别所造成的,但均在误差合理控制范围内,说明该实体模型的建立符合计算要求。

图8 仿真结果与试验结果比对Fig.8 Comparison of simulation results with test results
4 共振裕度分析
发动机叶片在不同转速下工作时,受外界复杂环境及不同激励载荷的影响,会激发出多种形式外激力,主要包括结构产生的机械力和空气流动造成的气动力。其中一部分力会随工作过程的变化呈现出周期性变动,而这些周期性变化的力也是迫使发动机叶片发生强迫振动的激振力。激振力的组成分为两部分:一是由于转子的不平衡导致零件产生交变力载荷引起的机械激振力;二是空气在流动过程中会与各通道内部的有效零部件之间产生间隙阻隔现象,造成气流流场分布不均衡,从而引发尾流激振力。所以当出现上述类型激振力的频率与发动机叶片的固有频率相等或成倍数时,就会发生共振现象。此时发动机叶片整体的振幅达到最大、内部振动应力值骤增,极易造成叶片疲劳寿命的缩短、叶片本身的疲劳损伤以及内部裂纹萌生等现象[16]。
4.1 计算结果分析
为进一步明确航空发动机工作过程中叶片的共振特性,需要基于一种特殊曲线的坐标图展开分析研究,即Campbell图,共振图[23]。当在Campbell图中出现激振力的频率曲线与不同转速下的动频曲线发生相交时,可以确定共振转速。这要求发动机涡轮叶片在前期设计时,其共振转速与工作转速的共振裕度要大于10%[17-20]。通过查阅航空发动机设计手册及相关文献,发现叶片的个数及排列布置方式会影响激振力的频率。外界激振力频率的计算公式为[4-5]

式中:fB为叶片的激振力频率,Hz;K为叶片的结构系数(K=1,2,…,n),其最大值为三级转子涡轮叶片的个数25,N为工作转速,r/min。
由于在低频区域段内振幅较高、危险较大,所以K值一般取到前3阶。结合表2中涡轮叶片不同工况下的固有频率,绘制的Campbell图如图9所示。图9中,叶片每阶的固有频率趋势线与外激振力频率线的交点即为有效共振点,该点处对应的转速值即为共振转速。一般情况下,将共振转速与工作转速附近的区域划分为危险区域。所以在叶片的前期设计及制造时尤其注意。本章节所研究的共振裕度校核分析也就是针对共振转速而言。
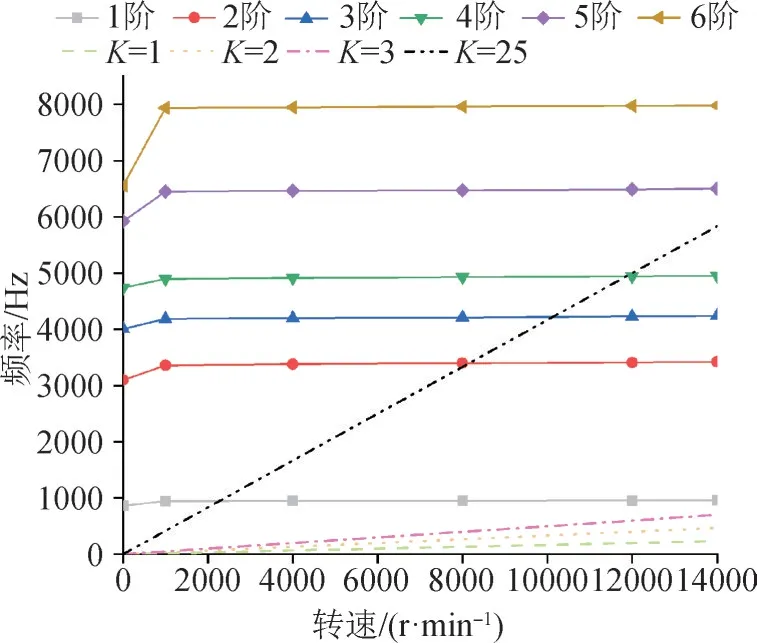
图9 坎贝尔图Fig.9 Campbell diagram
从图9可以看出,K倍激振频率线与涡轮叶片不同转速下前6阶的所有固有频率线存在4个交点,也就意味着存在4个比较危险的共振点。特别是在K=1,2,3的激振力射线与叶片各阶固有频率曲线上无交点。因此需要着重对K=25的激振频率曲线进行共振裕度校核。共振裕度校核计算公式为

式中:δ为共振裕度;N共振为共振转速,r/min;N工作为工作转速,r/min。
共振裕度校核结果如表4所示。

表4 共振裕度校核结果Tab.4 Resonance margin check results
从表4中涡轮叶片的共振裕度校核结果可以看出:叶片在飞行慢车和爬升的工况下会存在共振裕度小于10%的情况,其余工况[8]均满足共振裕度都大于10%的条件。因此,在叶片的前期设计及制造过程中,应尽量避免易引起叶片共振或谐振的工况,或在实际运行下,注意调节相应工况下的转速即可。
5 总结
基于ANSYS有限元模态分析理论和方法,求解了发动机涡轮叶片在不同转速下的固有频率和模态振型。通过与激光测振仪的测量结果进行比对,发现了ANSYS仿真计算结果与试验法模态分析结果趋势保持一致,两者之间误差较小;确定了仿真三维模型构建的正确性与实用性。
采用构建合理的仿真模型,绘制了该涡轮叶片在不同工作转速下的Campbell共振图。发现了K倍激振频率与叶片的固有频率共有4个交点,即4个共振转速,分别对应最大转速的16.2%、58.4%、72.9%及85.6%最大转速。通过与发动机涡轮叶片的工作转速进行共振裕度校核分析,发现只有在发动机慢车状态下会出现共振裕度小于10%的情况。因此建议发动机由慢车状态调整到最大转速时,应进行快速调节,以保证安全通过共振转速;且在叶片的前期设计制造时应进行结构的合理优化,从而避免共振现象的出现。
