干扰吸收峰影响下TDLAS温度测量方法研究
2022-10-19梅园园蔡静常海涛许江文
梅园园,蔡静❋,常海涛,许江文
(1.航空工业北京长城计量测试技术研究所,北京 100095;2.中国计量大学计量测试工程学院,浙江 杭州 310018)
0 引言
可调谐半导体激光吸收光谱技术(Tunable Diode Laser Absorption Spectroscopy,TDLAS)利用被测气体组分对激光的共振吸收,使激光能量产生衰减,进而对气体参数进行分析和判断,具有灵敏度高、非侵入性、响应速度快等优点,可实现温度、组分浓度、压强等流场多参数的在线高精度测量,已经成为流场诊断领域中一种非常重要的检测方法[1-2]。根据激光器加载的扫描信号不同,TDLAS技术可以划分为波长扫描调制吸收法和波长扫描直接吸收法。
波长扫描直接吸收法是TDLAS测量中最简单常用的实验方法,可通过波长调谐获得整个分子吸收线型,在实际应用中,往往需要根据所测的透射光信号得到积分吸光度,进而反演出所需流场参数。目前普遍采用Voigt或Lorentz线型对测量的直接吸收光谱进行拟合及数值积分,获取光谱的积分吸光度值,以减小测量过程中背景噪声的干扰[3-4]。基于直接吸收双线比值法测温时很难筛选出主吸收峰旁边没有任何干扰吸收峰的谱线对,主吸收峰旁边会叠加一些幅值较小的干扰吸收峰[5-9]。在这种情况下,为简化光谱数据处理算法,可忽略小的干扰吸收峰,对测量吸收光谱单峰拟合后进行温度反演,但对拟合结果准确性存在一定影响,会增大温度反演误差[8-9]。
针对目前TDLAS波长扫描直接吸收法测温领域存在的干扰吸收峰影响温度测量准确性的问题,本文在现有的线型拟合基础上,提出一种基于线型对称的积分吸光度计算方法,排除干扰吸收峰对温度测量的影响。使用SDAS双线比值法,根据吸收光谱仿真数据进行温度反演计算,并在实验室环境下搭建一套TDLAS测量系统,进行管炉测温实验,验证存在干扰吸收峰时,根据线型对称性获取积分吸光度进行温度测量的可行性。
1 测量原理
1.1 TDLAS测温基本原理
TDLAS技术的测量原理基于Beer-Lambert定律,即

式中:α为吸光度;v为频率,cm-1;It为穿过气体介质后的出射光强度;I0为入射光强度;P为气体总压强,atm;Xabs为吸收气体摩尔浓度;S(T)为谱线强度,cm-2·atm-1;L为光程,cm;φV为吸收线型函数,cm,其积分面积满足归一化特性。
温度为T时,谱线强度S(T)可表示为
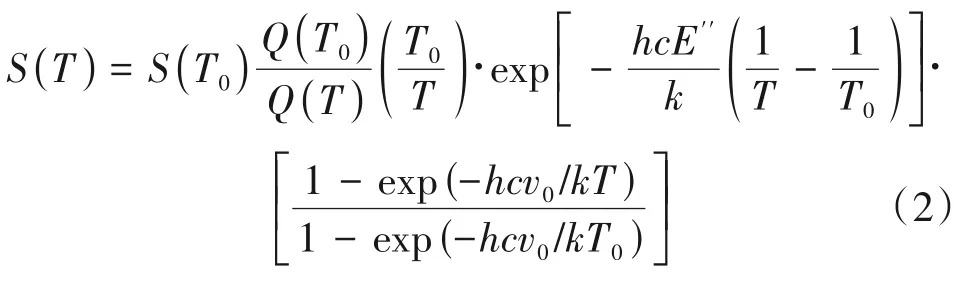
式中:S(T0)为参考温度T0下的谱线强度,可通过HITRAN光谱数据库查到其具体大小;Q(T)为吸收分子的配分函数,常用温度的分段函数来表示[10];h为普朗克常数,J·s;c为光速,cm/s;k为波尔兹曼常数,J/K;E''为吸收跃迁的低态能量,cm-1;v0为吸收线的中心频率,cm-1。
对吸光度α(v)在频域上积分得到积分吸光度A,它表示吸收谱线覆盖的面积,即
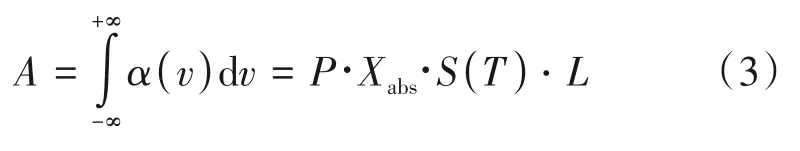
假设待测场内温度、浓度分布均匀,经过同一光路的两条吸收谱线的积分吸光度的比值是温度的单值函数,因此可求得激光路径上的平均温度,即
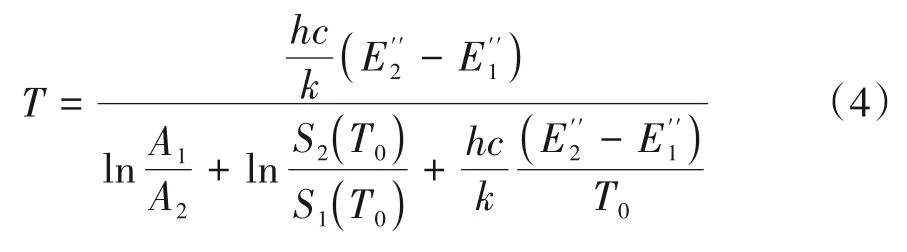
式中:A1和A2分别为两条吸收谱线的积分吸光度;E''1和E''2分别为两条吸收谱线的低态能量,cm-1。
由式(4)可知,在两条测量谱线确定的情况下,温度测量的准确性取决于两吸收谱线的积分吸光度,即吸收谱线覆盖的面积计算准确与否。根据基线拟合未吸收区域选择的“经验法则”[11],若获得的吸收光谱曲线在距中心频率四倍线宽范围内,除主吸收峰外无其余吸收峰,则可认为无干扰吸收峰,此时可利用谱线的全部信息获得积分吸光度;反之则认为存在干扰峰,其会对吸收谱线覆盖面积值的计算产生影响,需要考虑消除干扰。
1.2 基于对称的Voigt线型拟合
在燃烧研究中,实际的吸收谱线常用Voigt线型函数来描述,该函数为高斯线型函数与洛伦兹线型函数的卷积积分,其表达式为

对于Voigt吸收线型,吸光度α(v)可以表示为积分吸光度A和Voigt线型函数φV(v)的乘积
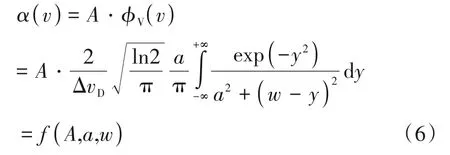
由式(6)可知,Voigt线型的非线性依赖于A,a,w三个参数,只能采用迭代方式进行非线性拟合来确定。根据文献[13]中的查表法来近似Voigt函数,采用遗传算法进行Voigt线型拟合。该算法以拟合曲线和实测曲线的残差平方和为适应度函数,将种群个体分别代入到适应度函数中,依据函数值大小分配适应度值:函数值越小,则拟合曲线和实测曲线的残差平方和越小,适应度值越大[14]。通过对多变量最优值进行搜索,得到给定范围内的最优拟合参数。
待拟合参数A,a,w初值设置如下:
1)利用线型函数关于中心频率v0对称,且在v0处取得最大值的特性,以波峰为标志,利用寻峰函数求得吸光度曲线的极大值位置。对中心频率至无干扰吸收峰一侧频率末端的吸光度进行数值积分,以积分值的2倍作为积分吸光度A的初值;
2)按光谱线宽定义,根据实测吸收光谱数据获得谱线半宽的初值Δv,并设定Δv=ΔvD=ΔvC;
3)由式(5)计算得出拟合参数a,w的初值。
Voigt线型拟合的流程图如图1所示,其中实测曲线为中心频率至无干扰吸收峰一侧频率末端。该拟合方法根据中心频率至无干扰吸收峰一侧频率范围的吸光度即可得到全频域的积分吸光度,不受干扰峰频域段的影响。
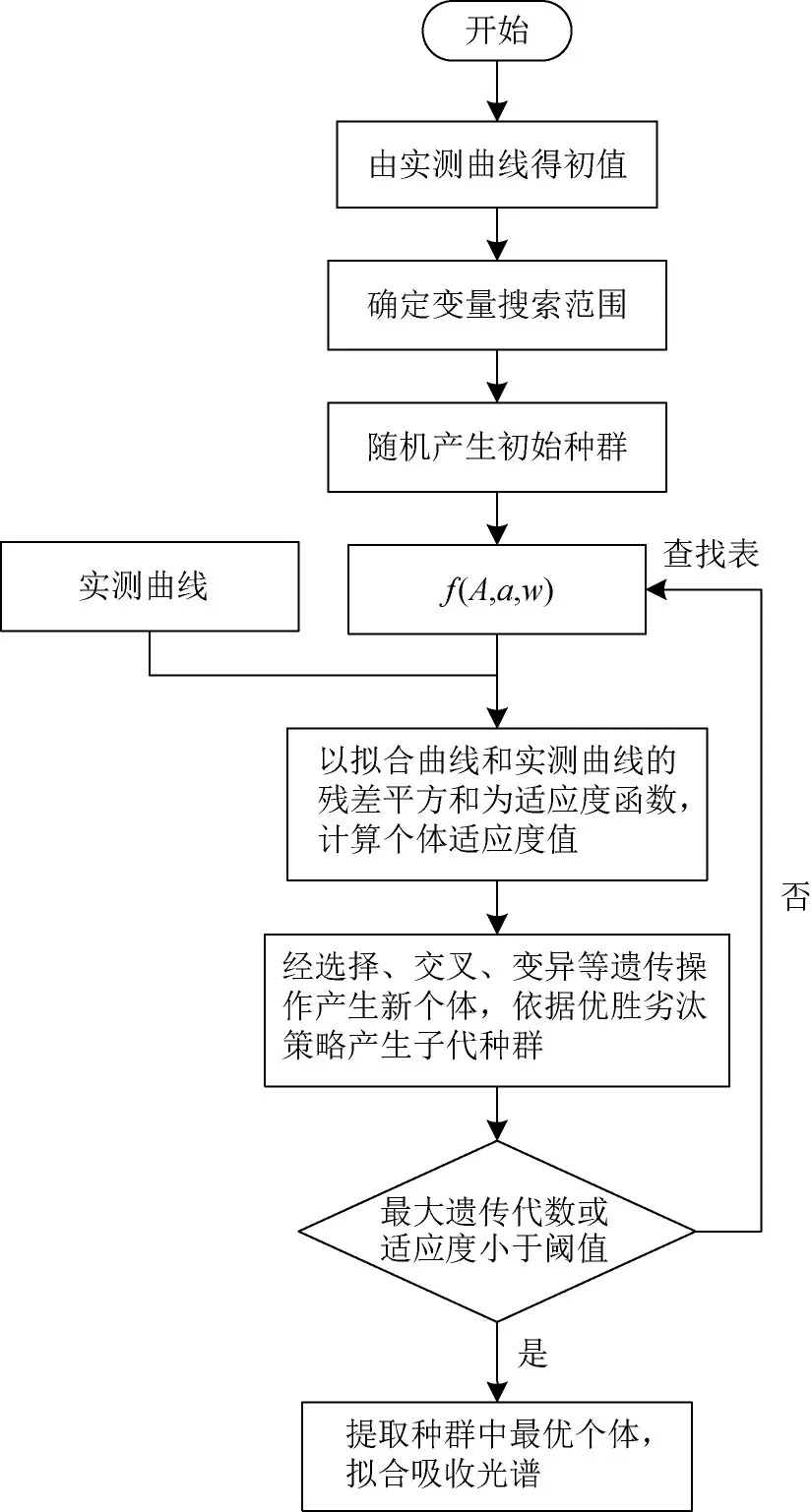
图1 遗传算法流程图Fig.1 Flow chart of genetic algorithm
2 实验系统
为验证根据吸收线型对称性获取积分吸光度进行温度测量的可行性,在实验室搭建了一套TDLAS测量系统,实验装置主要由激光光源、激光控制器、TDLAS中温标定炉、探测器及数据采集处理系统构成,实验系统整体结构示意图如图2所示。
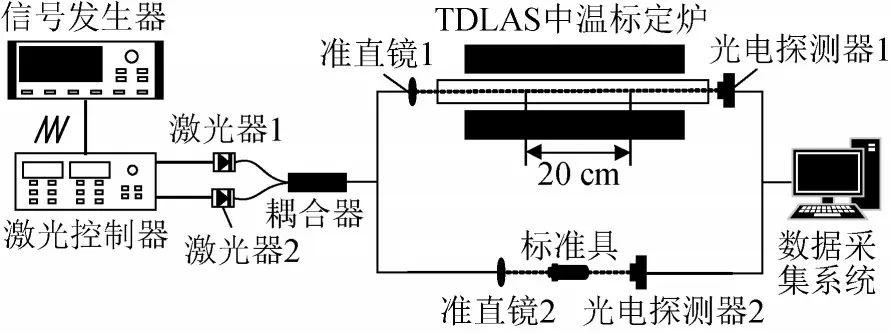
图2 TDLAS测量系统装置示意图Fig.2 Schematic diagram of TDLAS measurement system
3 仿真分析及实验结果讨论
3.1 仿真分析
在仿真过程中通过斯坦福大学开发的Spectra-Plot光谱数据模拟平台获取吸收光谱数据[16]。在压强为1 atm,光程为10 cm,温度为1000 K,浓度为20%的环境下用Voigt线型模拟了两条谱线的吸收光谱,如图2所示。7185.6 cm-1的吸收光谱在主吸收峰短波方向有一个小的干扰吸收峰,7444.4 cm-1的吸收光谱在主吸收峰长波方向有两个小的干扰吸收峰。
根据仿真数据,分别选择不同的积分范围计算积分吸光度,进行温度解算,计算结果见表1。

表1 不同积分范围温度计算结果Tab.1 Temperature calculation results in different integration ranges
实验选用TDLAS测量中常用的7185.6 cm-1和7444.4 cm-1两条H2O吸收谱线[15],由两个DFB激光器(型号为NLK1E5GAAA)及相应的驱动系统分别获得。根据激光器工作特性曲线,对信号发生器(型号为NF WF1968)和激光控制器(型号为ILXLightwave LDC-3724C)的参数进行设置,以对激光器进行电流调制,使其输出波长在所选谱线中心波长附近重复扫描。入射光经过2×2分束器分为两路,一路激光经过准直镜(型号为Zolix CFC-5X-C)后入射到待测温度场,作为被测的透射光信号;另一路激光经过自由光谱范围为1.5 GHz的标准具(型号为ThorsLab SA200-12B),采集干涉信号,用于对激光器输出光波长进行标定。两路光信号均通过探测器(型号为ThorsLab PDA20CS2)转换为电信号后由基于Labview软件实现的光谱数据采集系统保存。
实验所用的TDLAS中温标定炉可提供长度为20 cm,温度为100~1000℃均匀、稳定的高温环境,温度控制误差为±2℃。测量时,两侧腔内通入干燥的N2吹扫,以消除非恒温区中H2O对测量结果的影响。实验过程中,管炉温度范围设定为573~1173 K,每隔100 K取一个测量点。

图3 两条谱线的吸收光谱仿真图Fig.3 Simulation diagram of absorption spectrum of two spectral lines
通过表1可知,7185.6 cm-1及7444.4 cm-1谱线主吸收峰旁边的干扰吸收峰对温度反演结果有影响,根据对称性计算积分吸光度可消除干扰吸收峰的影响,提高温度计算准确性。
根据线型函数的对称性获取积分吸光度,采用仿真吸收光谱数据计算仿真温度点分别为400,600,800,1000,1400,1800,2200,2600 K时的温度值;忽略干扰峰的影响,对全频域段采用单峰拟合的方法计算各点的温度值用于对比。计算结果见表2和图4,可知基于线型对称法的温度测量平均相对误差为1.11%,而单峰拟合法的温度测量平均相对误差为5.66%,证明基于线型对称法的温度测量方法是可行的。
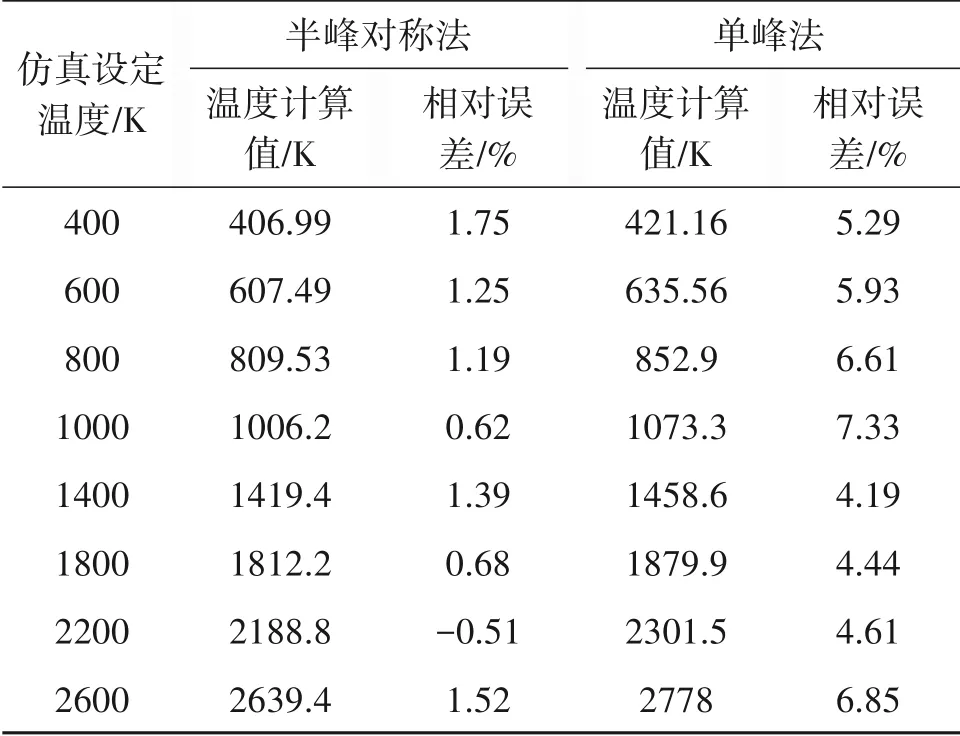
表2 不同仿真温度下温度计算结果Tab.2 Temperature calculation results at different simulation temperatures

图4 TDLAS仿真计算温度Fig.4 Temperature calculated by simulation
仿真吸收光谱温度反演误差存在的原因为:基于线型函数满足归一化条件,理论上积分吸光度是全频域积分的结果。在实际计算中,为排除其他频域处吸收谱线的影响,假设吸收光谱除了主吸收峰外,其余频率处吸光度值近似为0,将积分范围从无穷大缩小为主吸收峰附近一定频域,会使积分面积有所损失,使得计算结果存在不可避免的误差。
3.2 实验结果与讨论
使用100 Hz锯齿波扫描信号对DFB激光器进行调谐,以温度873 K为例,将所采集的透射光信号、标准具信号进行100次扫描周期平均,以消除激光器和探测器的随机噪声,平均后的信号如图5所示,并在其中标出了无吸收部分示意区域。标准具信号中峰与峰之间的频率间隔为标准具信号的自由光谱范围,根据标准具信号峰值点信息,利用三次样条插值,可将采样点的时域信号转换为频域信号。
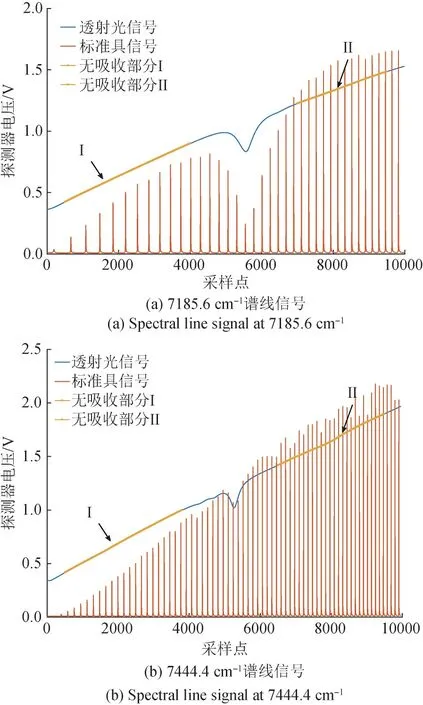
图5 周期平均后的透射光信号和标准具信号Fig.5 Transmission signal and etalon signal after periodic averaging
选择透射光It中无吸收部分进行三次多项式拟合,确定入射光强I0,然后通过(-ln(It(v)I0(v))计算吸光度得到测量的吸收光谱,之后进行Voigt线型拟合,获得吸收谱线的积分吸光度。由于7185.6 cm-1的吸收光谱在主吸收峰短波方向有一个小的干扰吸收峰,7444.4 cm-1的吸收光谱在主吸收峰长波方向有两个小的干扰吸收峰,它们与主吸收峰部分重叠在一起,考虑到线型函数的对称性,拟合时仅拟合主吸收峰中心波数至无干扰频域段。积分吸光度的初值为原始吸收光谱中心频率至无干扰频域段吸光度数值积分的两倍。实验测量吸收光谱和拟合结果如图6所示。
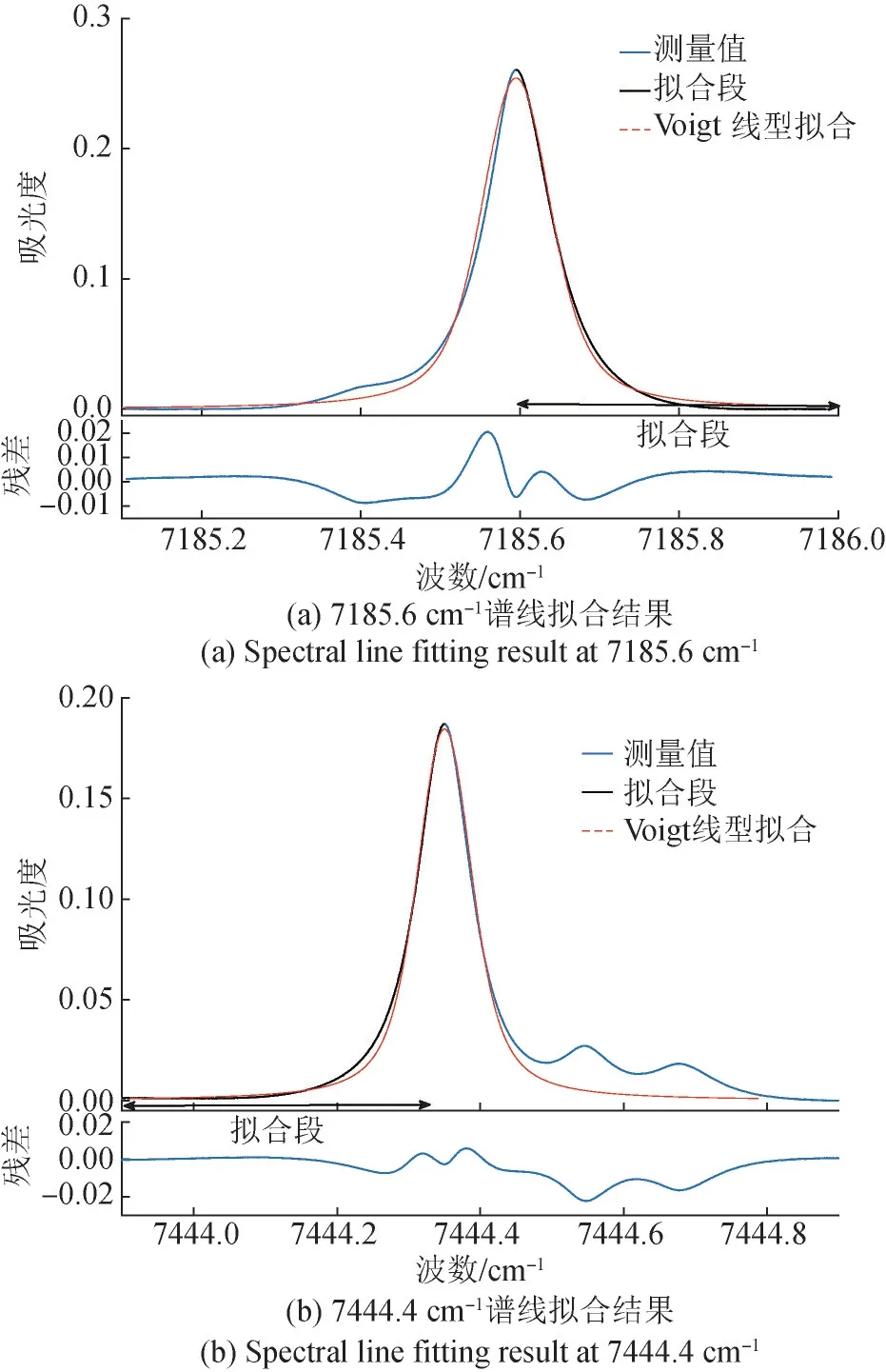
图6 实验测量吸收光谱与Voigt线型半峰拟合结果Fig.6 Half peak fitting results of absorption spectrum measured experimentally and Voigt lineshape
积分吸光度分别选择初值和半峰拟合值,根据式(4)计算标定炉温度;并计算忽略干扰峰影响,对主吸收峰直接进行单峰拟合后的温度,与标定炉设定温度进行对比,计算结果和相对误差见表3和图7。

表3 不同积分吸光度获取方式下温度测量结果Tab.3 Temperature measured with different integral absorbance acquisition methods

图7 TDLAS温度测量结果Fig.7 Temperature measured by TDLAS
根据表3可知,根据吸收光谱线型对称性得到积分吸光度初值,经Voigt线型半峰拟合后测量温度的平均相对误差为1.02%。图7表明,使用该方法得到的测量温度与标定炉设定温度具有较高的一致性。而单峰拟合的测量温度平均相对误差为9%,其中温度低于873 K时,测量温度的平均相对误差为1.81%;温度高于873 K后,测量温度的平均相对误差为14.4%,产生此现象的原因是温度升高后,7444.4 cm-1谱线主吸收峰长波方向干扰吸收峰变大,对测量结果影响增大。
4 结论
针对波长扫描直接吸收法测温准确性受干扰吸收峰影响的问题,提出了根据吸收光谱线型对称性获取积分吸光度的方法。基于吸收光谱线型函数关于中心频率对称,且在中心频率处取得最大值的特性,根据中心频率至无干扰吸收峰一侧频率范围的吸光度,利用对称性计算得到全频域的积分吸光度,以此来排除干扰吸收峰对测温准确性的影响。使用吸收光谱仿真数据进行了温度计算,并在实验室环境下进行了实验验证。使用线型对称法,仿真计算和实验测量得到的温度平均相对误差分别为1.11%和1.02%;使用忽略干扰峰影响的单峰法,仿真计算和实验测量得到的温度平均相对误差分别为5.66%和9%,证明根据线型对称性获取积分吸光度的方法可有效消除干扰吸收峰的影响,提升温度测量准确性,特别是在873 K以上的高温段,使用线型对称法的优势更为明显,为提升TDLAS波长扫描直接吸收法测温技术的准确性与可靠性提供了有力支撑。
