基于斯格明子的自旋转移矩纳米振荡器的微磁学模拟

吴圆圆，路炳文，王炳峰，蔡廷涛，许玉鑫，周安航，张 召，胡成超

(聊城大学 材料科学与工程学院，山东 聊城 252059)

0 引言

斯格明子是一种受拓扑保护且具有手性自旋结构的纳米磁性粒子，最早由英国核物理学家Tony Skyrme[1]提出，作为一种拓扑孤子用于描述介子与重子统一场理论。大量研究显示斯格明子可以在玻色-爱因斯坦凝聚[2]、液晶[3]和量子霍尔体系[4]等中存在。随后，Rößler[5]等在理论上预言了斯格明子可以在具备空间反演对称性破缺的磁性薄膜或体材料中存在。直到2009年Mühlbauer[6]等在B20族化合物MnSi中通过小角度中子散射实验观察到斯格明子的存在，以及多个课题组在不同材料和结构体系的室温零场下[7-12]观察到斯格明子可以稳定存在将斯格明子推向研究热点。由于斯格明子具有体积小、结构稳定以及易受外加激励驱动的特性，被广泛认为有望成为新一代自旋电子器件的信息载体。

斯格明子作为信息载体，可以应用于赛道存储器[13-15]、自旋转移矩纳米振荡器(Spin Torque Nano-Oscillator, STNO)[16-18]、晶体管[19]、逻辑器件[20]和类脑器件[21]等自旋电子器件。其中，自旋转移矩纳米振荡器作为新一代的微波振荡器，是斯格明子作为信息载体非常重要的一项应用。微波振荡器利用频率合成技术产生需要的频率或波形信号，在微波毫米波仪器及系统应用范围广、需求大，是微波信号发生器的核心部件。传统的振荡器件以LC振荡电路为核心，具有线宽大、可调谐振幅窄[22](仅15%)的缺点。因此，人们提出了一种基于磁电阻效应和STT(spin transfer torque) 效应的自旋转移矩纳米振荡器[23]。这种新型器件主要有两种可选择的信息载体，即磁涡旋[24]和磁性斯格明子[25]。由于斯格明子无论是在尺寸、稳定性以及驱动电流大小上均优于磁涡旋，被认为是STNO的优良信息载体。基于斯格明子的自旋纳米振荡器具有低能耗、高输出功率以及宽频可调性，因此，研究斯格明子在材料中的稳定存在因素以及纳米圆盘中电流驱动斯格明子的动力学行为，对于基于斯格明子的STNO的研发具有重要意义。

本文运用微磁学模拟方法研究了斯格明子在电流密度和DMI (Dzyaloshinkii-Moriya interaction) 常数下的存在区间以及尺寸变化，分析了边界效应以及STT等对斯格明子的作用，模拟了斯格明子在纳米圆盘中不同电流密度和DMI常数下的动力学行为，最后探究了斯格明子个数对振荡器能效的贡献，为基于斯格明子的自旋纳米振荡器的设计与器件化提供理论预测和指导。

1 模型与方法

本文使用基于有限差分法的三维微磁学模拟软件OOMMF(Object Oriented MicroMagnetic Framework)，对基于斯格明子的STNO进行微磁学模拟. 磁演化采用包含DMI、STT和适当边界条件的LLG(Landau-Lifshitz-Gilbert)方程[26,27]

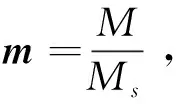
其中Λ为自由层和极化层的不匹配系数，P为电流极化率，J为电流密度，e为电子电荷，t为自由层厚度，Ms为饱和磁化强度。自由层磁矩在自旋转移力矩和阻尼的作用下的力矩分析如图1所示。

本文采用STNO模型是一个MTJ结构，它由钉扎层、间隔层和自由层组成，如图2所示。其中钉扎层采用的材料是重金属，作用是为MTJ提供自旋极化电流，并与自由层共同产生磁阻效应；间隔层采用的材料为MgO，用来隔绝钉扎层和自由层之间的层间耦合，提高自由层磁矩对电流的响应；自由层实际由CoPt双层膜组成，CoPt双层膜的界面能够为存在于Co膜中的斯格明子提供面DMI。图中黄色部分为电极，用于注入自旋极化电流。本工作中我们分别通过电极对STNO施加极化方向为-z和+z方向的自旋极化电流，进而对斯格明子在STNO中的形核和驱动进行研究。由于在OOMMF中，我们可以通过代码等效替代钉扎层和间隔层的作用。因此，本工作中我们皆以自由层作为模型进行运算，下文便不再赘述。

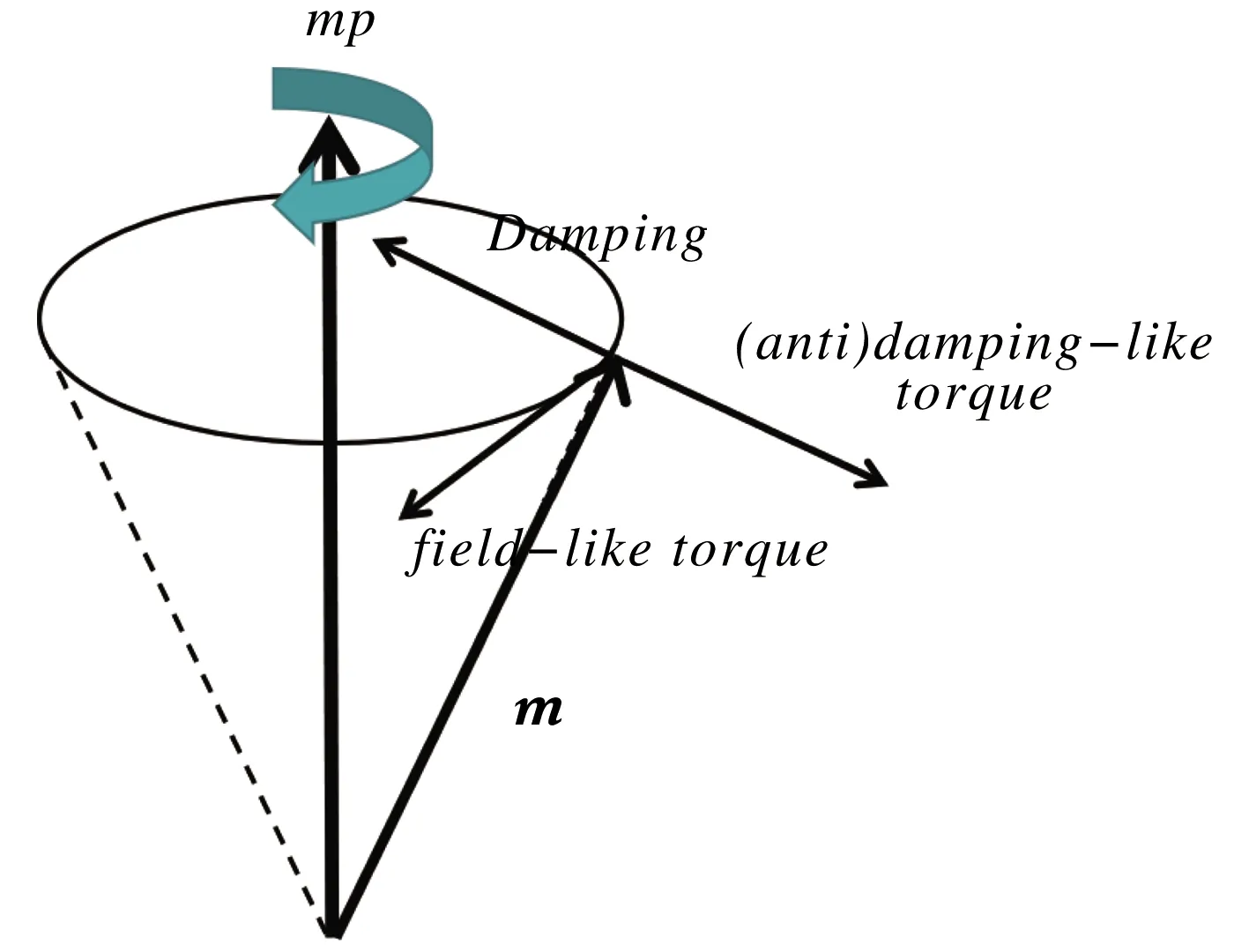
图1 自由层磁矩在电流有效场和阻尼作用下的力矩分布图

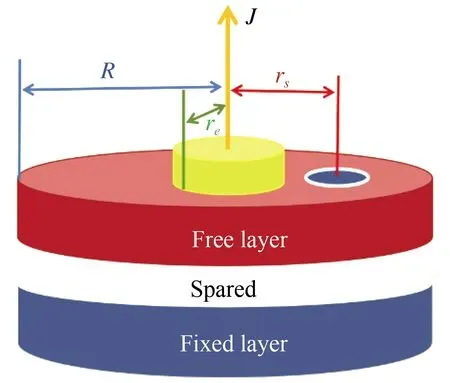
图2 由钉扎层、隔离层、自由层组成的纳米圆柱示意图[25]

本文的模型尺寸：圆盘底面直径d=60 nm,厚度t=1 nm，离散化单元尺寸为1.0 nm×1.0 nm×1.0 nm。如无特殊说明，本文采用如下材料参数：交换常数A=15 pJ/m，垂直各向异性常数Ku=0.8 MJ/m3，LLG阻尼因子α=0.3，Gilbert旋磁比γ=2.21×105，饱和磁化常数Ms=0.8 MA/m，电流自旋极化率P=0.4，不匹配系数Λ=1.0。

2 结果与讨论

2.1 纳米圆盘中电流诱导斯格明子成核

在纳米圆盘中，斯格明子具有一定的存在区间，例如：自旋极化电流诱导斯格明子成核时具有最小的阈值电流，否则较小的电流不足以提供克服普通铁磁性结构与斯格明子之间拓扑壁垒的能量，而较大的电流可能使自由层磁矩全部翻转导致斯格明子湮灭；现阶段发现可以稳定存在斯格明子的材料较少，这是由于斯格明子要求材料具有一定的DMI和强垂直各向异性。为此，我们首先探究了不同大小的DMI及电流密度下斯格明子的形核情况，如图3所示。

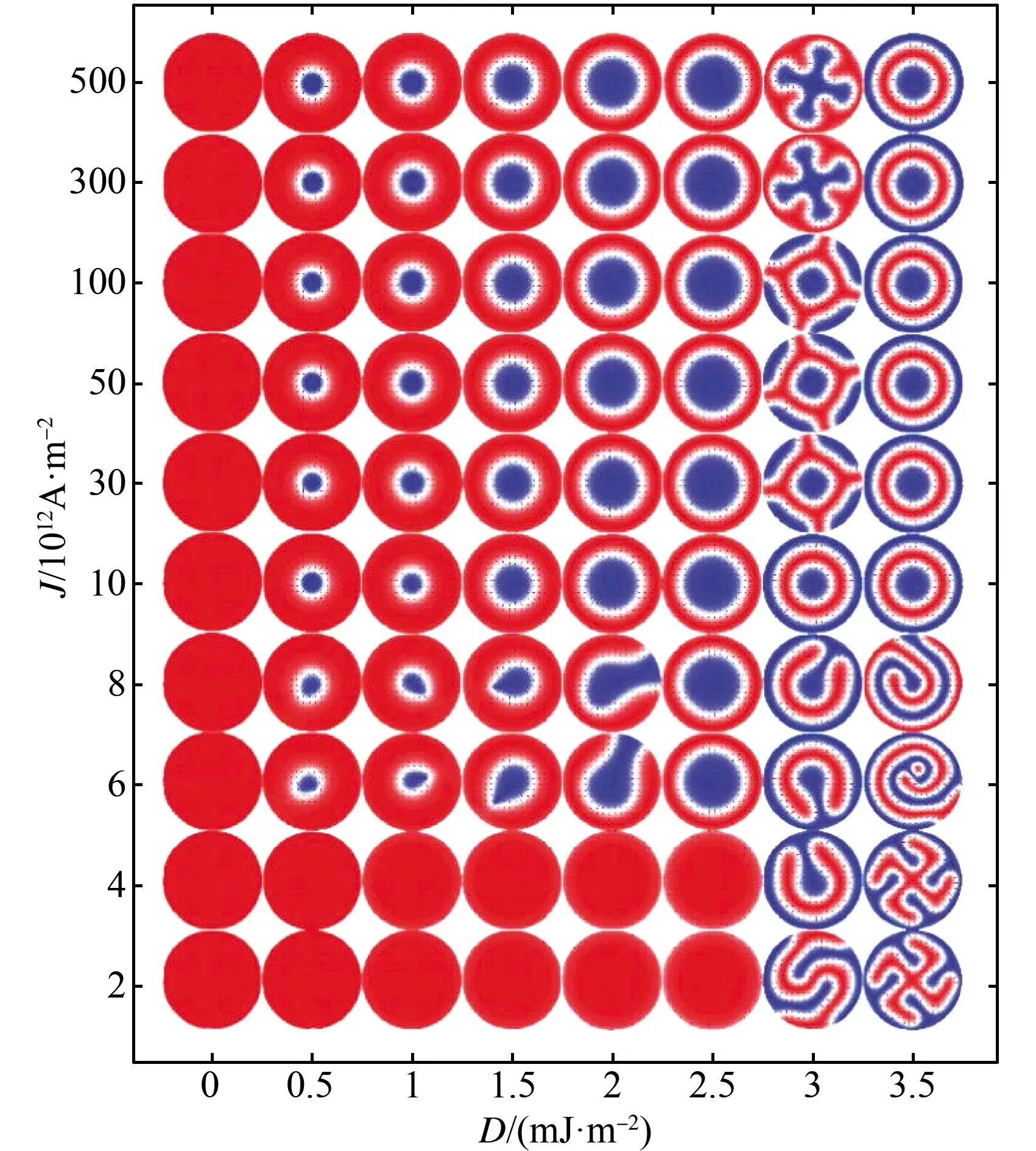
图3 不同大小的DMI常数和电流密度J下 纳米圆盘的磁化状态

从图中我们可以看出，在注入极化方向为-z的极化电流时，对于没有DMI即D=0时的纳米圆盘，无论施加多大的电流，都不能产生斯格明子，甚至不能使磁盘局域磁矩翻转。而只需要极小的DMI，将D调大到0.5 mJ/m2，从电流达到一定值开始，纳米圆盘发生局部磁矩翻转，产生磁泡等拓扑平庸结构，这是由于DMI和垂直各向异性的存在有利于磁矩在空间中连续变化并稳定存在。此时，若电流增大到10×1012A/m2，斯格明子将在纳米圆盘中生成并稳定存在。不难看出，随着DMI的增大，斯格明子尺寸逐渐增大，并且形核阈值电流有减小趋势。D在0.5～2.0 mJ/m2区间内，随着电流的增大，纳米圆盘的稳定磁态经历了由初始磁态过渡到普通磁畴或磁泡，再由普通磁畴或磁泡过渡到斯格明子的过程。并且在电流逐渐增大的过程中斯格明子的尺寸有变大的趋势，但并不明显。当D增大到3.0 mJ/m2时，由于DMI太大，导致边界效应过强，甚至在不加电流的情况下就会由边界开始发生磁矩的翻转，并逐渐扩展，产生不规则的的磁畴结构。此时随着电流的增大，纳米圆盘中的磁态不断变化，由形状不规则的磁畴变为形状对称的磁畴，而在电流达到300×1012A/m2及以上时，圆盘磁矩会发生复杂变化，最后形成与小电流下截然相反的外红内蓝式规则畴壁。当D进一步增大到3.5 mJ/m2时，随着电流的增大，圆盘磁态经历了风车式磁畴、迷宫畴和双重斯格明子三种磁化状态。值得一提的是，在D=3.0～3.5 mJ/m2的区间内，除了双重斯格明子，其他畴结构无论形状是否规则，无论施加电流密度或大或小，畴结构都会在纳米圆盘中不断转动。

2.2 单个斯格明子在纳米圆盘中的振荡

在探究DMI及电流密度对斯格明子形核情况的影响之后，我们开始探究单个斯格明子在纳米圆盘中的振荡，并分析了它的动力学行为。振荡模型如图2所示，将单个斯格明子放置在圆盘边缘并通过注入极化方向为+z的反向电流(与诱导斯格明子成核时注入的-z极化方向电流方向相反)驱动斯格明子进行振荡。在本小节，采用的DMI系数为2.7 mJ/m2。

图4 (a) 未加电流时，单个斯格明子在纳米圆盘中的 运动轨迹；(b) 施加电流时，单个斯格明子 在纳米圆盘中的运动轨迹

本文并没有直接注入自旋极化电流诱导斯格明子转动，而是先模拟了未加电流时斯格明子的运动行为，如图4(a)所示。我们发现斯格明子会从圆盘边缘以螺旋形轨迹进动至圆盘中心。这是由于放置在边缘的斯格明子所受边界斥力并不均衡，处于一种高能量不稳定的状态，而当斯格明子处于圆盘中心时，受力均匀较为稳定，处于低能量态。因此，放置在边缘的斯格明子具有自发向圆盘中心运动的趋势。而马格努斯力、进动阻尼与边界斥力的共同作用则导致其运动轨迹为螺旋状。

下一步，我们在纳米圆盘中间注入d=5 nm，J=0.6×1012A/m2的反向电流。发现在该电流下，斯格明子尺寸急剧减小，后经过周期性变化稳定在一较小尺寸，同时在这一过程中斯格明子进行半径增大的外螺旋运动至一稳定轨道，并进行顺时针匀速圆周运动，如图4(b)所示。通过受力分析，不难发现加电流与不加电流时斯格明子运动行为不同的原因：在施加反向电流时，斯格明子受到沿运动轨迹切向的自旋转移力矩与阻尼力矩，两者方向相反。在电流足够大时，STT作用大于阻尼，赋予斯格明子切向速度以及顺时针运动方向。当斯格明子运动轨道半径达到一定大小时，沿径向向外的马格努斯力小于径向向里的边界斥力，二者形成向内合力，提供圆周运动所需的向心力。

图5 电流驱动单个斯格明子振荡时，进动半径rs、 进动频率f与电流密度J的关系

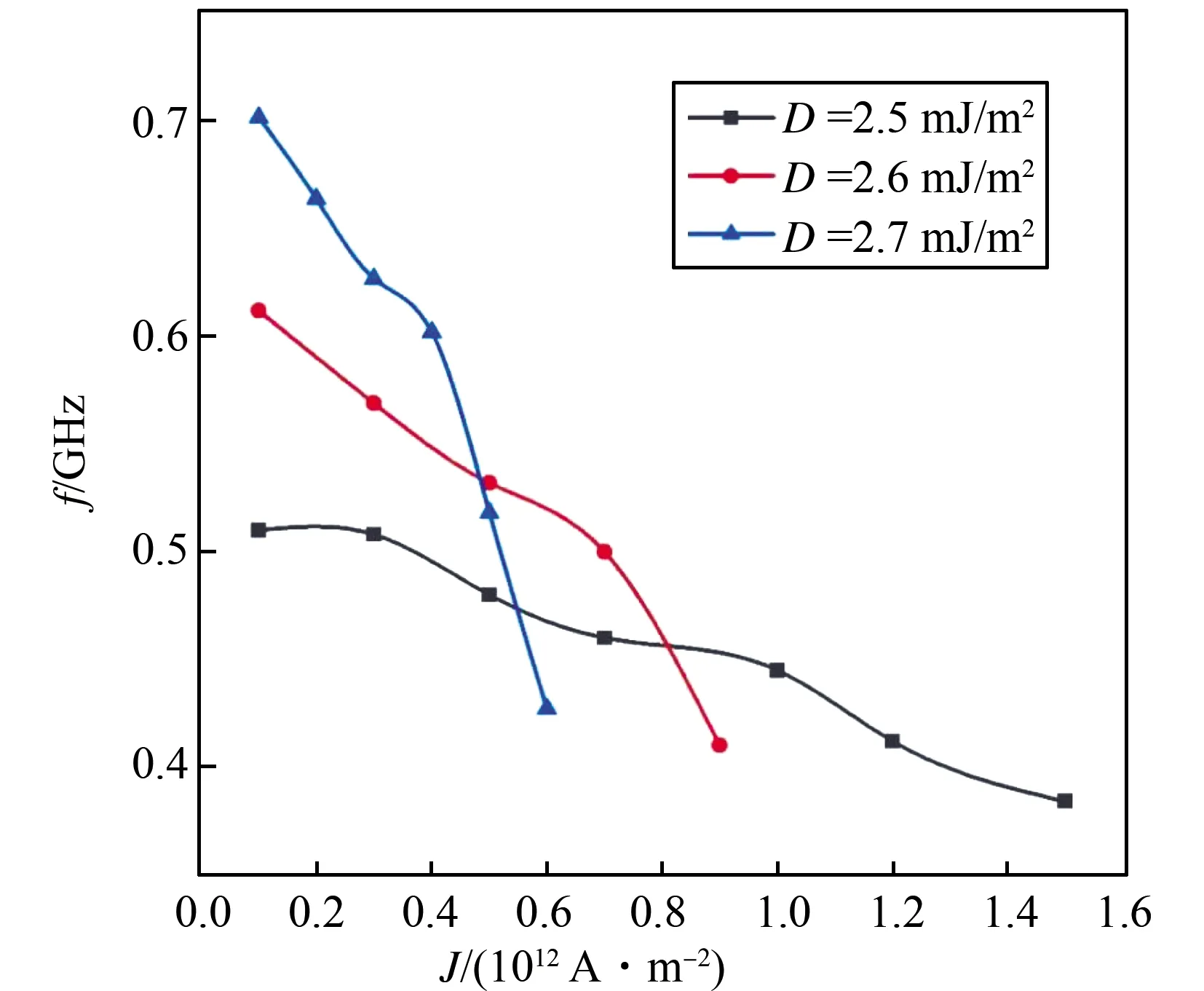
图6 不同DMI下斯格明子进动频率f与电流密度J的关系

为了进一步研究纳米圆盘中斯格明子的进动频率f，我们通过模拟不同电流密度下斯格明子的进动行为，得到电流密度J对斯格明子进动半径rs和进动频率f的作用规律，如图5所示。随着电流密度的提高，斯格明子所受的STT增大，切向速率提高，所需要的向心力增大。因此，斯格明子需要运动到边界斥力更强的轨道上去，对应于进动半径的增大。令人惊讶的是，随着J的提高，斯格明子进动频率f反而减小。我们推测这可能是因为rs越大斯格明子越靠近边界，而由于边界能量较高，磁矩翻转所需要的能量增大，斯格明子移动难度增加；且rs增大斯格明子转动一圈路径增长。这两点不但抵消了电流增大所导致的切向速率提高对斯格明子进动频率的增幅，而且使斯格明子转动一圈的时长增加，频率下降。

为了验证上述规律的普适性，我们对不同大小DMI下电流密度J对斯格明子的进动频率f的影响规律进行了探索，如图6所示。在不同大小的DMI下，斯格明子进动频率随电流密度的增加而减小，与图5结果保持一致。并且我们发现，由于在较小电流下DMI越强越利于磁矩在空间中连续分布，磁矩翻转越容易，因此斯格明子进动频率越高。如在电流密度为J=0.2×1012A/m2时，f随DMI常数的增大而增大。在提高电流密度的过程中DMI越大的模型，斯格明子进动频率下降速率越快。当J增大到0.6×1012A/m2的时候，D=2.7 mJ/m2模型中斯格明子最终湮灭；而增大到0.9×1012A/m2时，D=2.6 mJ/m2模型中斯格明子最终湮灭。这是由于DMI越强，斯格明子尺寸越大。但随着尺寸的增加，斯格明子在纳米圆盘中稳定进动的半径浮动区间越小，越容易触碰边界而湮灭。因此DMI越小，斯格明子可稳定进动区间越大，可稳定振荡的电流区间越大。最后我们发现DMI越大，STNO输出频率可调控区间越宽。

2.3 多个斯格明子在纳米圆盘中的振荡

在研究了单个斯格明子振荡情况的基础上，我们模拟了不同数量斯格明子在纳米圆盘中的运动过程，如图7(a)所示。在本小节中，单斯格明子模型与上文保持一致。在放置两个斯格明子和三个斯格明子时，我们分别按中心对称和以圆心为重心的等边三角形放置，目的是使各斯格明子受力均衡，保持稳定。模型尺寸、材料参数以及斯格明子距离圆心距离与单斯格明子模型保持一致。在施加J=0.6×1012A/m2的反向电流后，放置一个、两个、三个斯格明子的模型中均出现了斯格明子进动行为。其中，单斯格明子和双斯格明子模型中斯格明子均按顺时针进行圆周运动，反常的是三个斯格明子模型中斯格明子按逆时针进行圆周运动。进动期间，各斯格明子之间相对距离保持一致。从进动频率上来看，模型中斯格明子的数目越多，单体进动频率越小。然而，从STNO输出功率上来看，在检测器数量均为一个时，若要产生一个完整周期的微波信号，单斯格明子需要进动一周，双斯格明子则只需进动半周，三个斯格明子更是只需要进动三分之一个圆周。此时，三个斯格明子模型的STNO输出整体频率最高，双斯格明子其次，单斯格明子最小。

图7 (a) 以0.3 ns为间隔，一个、两个、三个斯格明子在纳米圆盘中的进动轨迹;(b) 以0.9 ns为间隔， 三个斯格明子在纳米圆盘中的运动状况

由于三个斯格明子模型出现了反常的逆时针进动行为，我们对三个斯格明子模型展开了进一步的研究。如图7(b)所示，我们以0.9 ns为间隔，记录斯格明子在圆盘中的进动轨迹。我们发现，在0～8.1 ns期间，斯格明子按逆时针进行圆周运动，与图7(a)结果保持一致，并且进动速率随时间递减，直到8.1 ns进动速率降低为零。从8.1 ns开始，斯格明子开始进行进动速率随时间不断提高的顺时针圆周运动，并在30 ns左右，开始进行匀速圆周运动，保持稳定。

3 结论

本文通过微磁学模拟软件OOMMF对自旋转移矩纳米振荡器中斯格明子在纳米圆盘中的产生和振荡机制进行了系统研究。自旋极化电流诱导斯格明子形核过程中，外加电流强度和材料本征DMI共同决定了材料最终的磁畴态. 斯格明子的形成需要外加电流达到特定的阈值，斯格明子的最终尺寸与DMI强度正相关. 对斯格明子在纳米盘中的进动和螺旋运动的动力学分析表明，斯格明子在特定轨道稳定振荡是材料的本征阻尼、纳米盘的边界斥力、马格努斯力以及自旋极化电流提供的STT效应等协同作用的结果：纳米盘材料和尺寸选定的条件下，斯格明子的振荡半径(和振荡频率)分别与自旋极化电流强度呈现正相关(和负相关)；考虑材料的DMI对斯格明子的振荡频率的影响时，要同时兼顾外加极化电流强度的大小. 多斯格明子振荡器模型表明，虽然单个斯格明子振荡频率有所降低，但是器件整体输出的振荡频率随着斯格明子数目的增多而增大. 本工作对于基于自旋转移矩斯格明子振荡器研发过程中的钉扎层、间隔层和自由层的材料选择、镀膜层数以及施加电流强度的大小具有重要的参考价值，对于缩短新型斯格明子振荡器的研发周期和降低研发成本具有重要的理论指导意义.