四元数矩阵方程最小二乘问题的半张量积解法

王 栋，李 莹，丁文旭

(聊城大学 数学科学学院，山东 聊城 252059)

0 引言

矩阵方程在计算机科学、量子物理、统计、信号与彩色图像处理、刚性力学、量子力学、控制理论、场论等领域有着广泛的应用[1-6]。因此，许多学者对不同代数结构上的矩阵方程都进行了研究，并使用不同的方法得到许多结果[7-15]。例如，Chu通过GSVD分解研究了实矩阵方程AXB+CYD=E，并给出了其最小二乘解[7]；徐使用 CCD分解得到了复矩阵方程AXAH+CYCH=F的最小二乘解和对称(反对称)解[8]；廖结合GSVD和CCD研究了复矩阵方程AXBH+CYDH=E的极小范数最小二乘问题[9]；王利用四元数矩阵的复表示研究了四元数矩阵方程AXB=C的最小二乘双对称解、斜对称解、中心对称解[11]；袁研究了四元数矩阵方程(AXB,CYD)=(E,F)的η-bi-Hermitian 解[13]；宋给出了多类广义Sylvester四元数矩阵方程解存在的充要条件和解的表达式[14]等等。

近些年来，程及其团队提出了矩阵半张量积(STP)理论[16]以解决非线性系统的线性化问题。STP打破了经典矩阵乘法在维数上的限制，并且有许多有趣的性质，比如换位矩阵、伪交换性等。大量学者将STP作为工具，已在博弈论[17]、图论[18]、逻辑系统[19]等多个领域取得了许多重要成果。

1 问题描述

我们将利用矩阵半张量积研究下列四元数矩阵方程的最小二乘问题

(1)

因为Hermitian矩阵在工程问题和线性系统理论中起着重要作用，我们将研究(1)的最小二乘Hermitian解。具体问题如下

问题1设Ai∈Qm×n，Bi∈Qn×q，C∈Qm×q，求

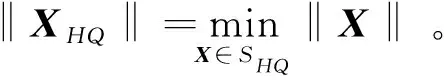
本文的结构如：第2节列举四元数矩阵和STP的基础知识。第3节提出一种四元数矩阵的实向量表示，并给出部分性质及证明。第4节用这种实向量表示、矩阵半张量积和MP逆来研究问题1。第5节提供算法和算例以验证第4节对于问题1 求解结果的准确性。最后，第6节进行简单总结。

2 预备知识

定义1[20]一个四元数q∈Q可以表示为q=a+bi+cj+dk，其中a,b,c,d∈R，三个虚部i，j，k满足i2=j2=k2=ijk=-1，ij=-ji=k，jk=-kj=i，ki=-ik=j。

定义2[21]设A∈Rm×n，B∈Rp×q，矩阵A和B的半张量积定义为A*B=(A⊗It/n)(B⊗It/p)，其中t=lcm(n,p)是n和p的最小公倍数。

如果n=p，矩阵A和B的半张量积就变成了矩阵经典乘法。因此，矩阵半张量积可以看作矩阵经典乘法的推广。

定理1[21]设A，B，C是实矩阵，a，b∈R，则下列性质成立

(1) (分配律)A*(aB±bC)=aA*B±bA*C，(aA±bB)*C=aA*C±bB*C；

(2) (结合律) (A*B)*C=A*(B*C)；

(3) 设x∈Rm，y∈Rn，则有x*y=x⊗y。

矩阵和向量的半张量积具有如下的伪交换性。

定理2[21]设x∈Rt，ω∈Rt，A∈Rm×n，则有x*A=(It⊗A)*x,A*ω=ω*(It⊗A)。

换位矩阵的作用就是交换向量的半张量积中两个向量的顺序。

定理3[23]设x∈Rm，y∈Rn，则下式成立W[m,n](x*y)=y*x。

3 四元数矩阵的实向量表示及其相关性质

我们将提出四元数矩阵的实向量表示并给出其部分性质及证明。首先介绍四元数的实向量表示。

定义5设x=x1+x2i+x3j+x4k∈Q，其中x1,x2,x3,x4∈R，定义

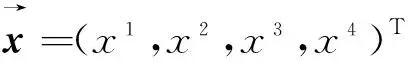
基于四元数的实向量表示，将四元数向量的每一个元素都实向量表示，即可得到四元数向量的实向量表示，如下。

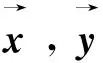
四元数矩阵的每一行(每一列)都是四元数向量，将矩阵按行(列)分块，即可通过四元数向量的实向量表示得到四元数矩阵的实向量表示，如下。

为四元数矩阵A的实行排形式。

下面给出四元数向量和矩阵实向量表示的性质。

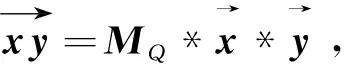
证明通过简单的计算，我们可得(1), (2)，下证(3)

根据定理5，我们可以得到下述四元数矩阵实表示的相关性质。

证明(1), (2), (3)显然成立,下证(4)

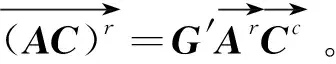
根据定理6和矩阵半张量积的相关性质，我们可以推出三个矩阵乘积的实向量表示，这是解决问题1的关键。

定理7设A∈Qm×n，B∈Qn×n，C∈Qn×q，则

(2)

(3)

同理，(3)式易得。

4 问题1的矩阵半张量积解法

本节我们将利用矩阵半张量积解法来求解问题1。利用Hermitian矩阵的特殊结构，我们将提取其独立元素进行计算，以简化运算规模。

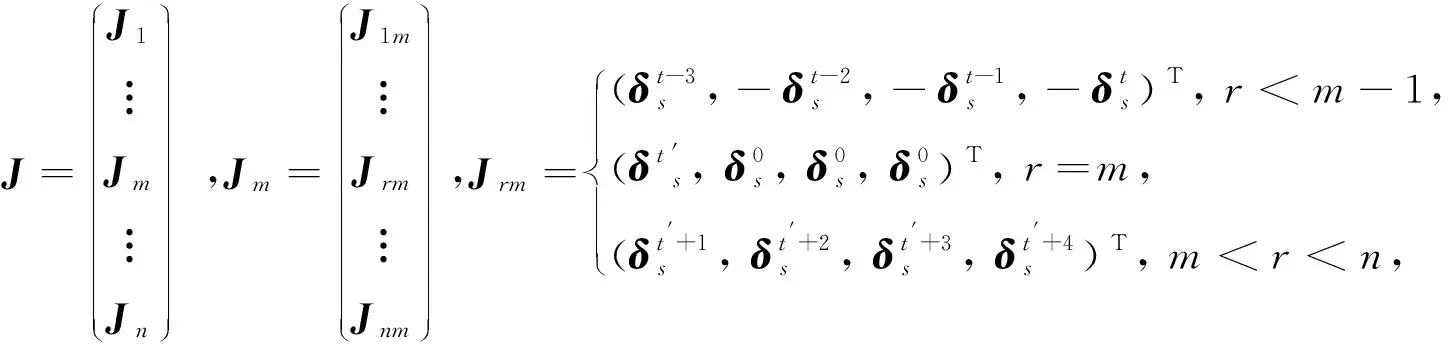
(4)

则问题1的解集可表示为

(5)

问题1的极小范数最小二乘Hermitian解XHQ满足

(6)

证明由定理7、定理8可得

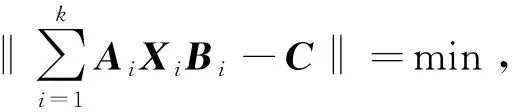
(5)得证。

由于

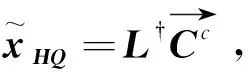
推论1 设Ai∈Qm×n，Bi∈Qn×q，C∈Qm×q,(1)有Hermitian解的充要条件是

(7)

其中L为(4)式。若(7)成立，则(1)的解可以表示为

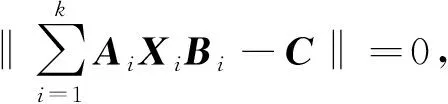
因此，对于任意X∈SHQ，都有

成立。

因此，若(1)有Hermitian解X，则X满足

由经典矩阵理论可知

5 数值算例

算法1

Begin

Step1 输入Ai∈Qm×n，Bi∈Qn×q，C∈Qm×q,G，G1′，J，W[4nq,4n2];

End

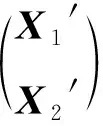
算例2取不同规模下四元数矩阵方程(1)，分别用实表示[24]、复表示[25]和实向量表示方法进行误差比较，使其进行k次，统计其最优次数，取k=30，三种方法的最优次数表如图2所示。

图1 不同维数下问题1的误差图 图2 不同维数下三种方法达到最优次数图

由图1可看出该算法的有效性，由图2可看出在维数变大时，实向量表示方法误差最小的概率会更大。

6 结论

本文提出了一种基于矩阵半张量积，求解四元数矩阵方程最小二乘问题的方法。利用此方法可以避免四元数乘积中冗杂的运算，将四元数矩阵方程转化为实矩阵方程，使求解过程更加简便。通过验证，该算法精度较高，可行性较强。