基于似然比方法的弹壳击针头3D 痕迹检验研究

谭铁君, 刘明星

(1.西南政法大学刑事侦查学院, 重庆 401120;2.重庆高校刑事科学技术重点实验室, 重庆 401120)

0 引言

枪弹痕迹检验可以分析事件性质、重建现场、串并案件和为诉讼提供证据,其在侦查和审判中的地位不容忽视。 在枪弹痕迹检验中,可利用弹壳痕迹鉴别枪支或枪支种类,检验涉及到的弹壳痕迹主要包括:击针头痕迹、弹底窝痕迹、抛壳挺痕迹等。 传统的弹壳痕迹检验方法主要依赖痕迹特征的形态比较和鉴定人的经验判断,检验结果主观性比较强。为了提高检验鉴定的准确性、可靠性和客观性,对痕迹特征进行定量测量,基于数据统计进行分析评判,逐渐成为枪弹痕迹检验技术发展的新趋势[1-2]。 早期弹壳痕迹特征测量的方法主要是基于读数显微镜进行二维特征的测量,特征数据精度和应用效力有限。 随着3D 光学测量技术的发展以及超景深三维立体显微镜的使用,对弹壳痕迹特征的三维数据精细化测量成为可能。 通过三维测量技术提取的弹壳痕迹特征不仅种类和维度更加丰富,而且也具有更高的鉴定价值[3-4]。 对于以击针头痕迹为代表具有明显三维特性的立体痕迹而言,三维测量技术具有更好的应用前景。 击针头痕迹是枪支射击后在弹壳底面形成的、能够反映枪械击针头外表结构特点的痕迹,该痕迹主要形成于发射过程中,因形成时火药气体压力产生的作用力极大,所以该痕迹深而明显,且反映稳定、不易被覆盖,对该类痕迹使用三维检测技术非常适合[5]。

随着法庭对检验鉴定的科学性和客观性要求的不断提高,国际上提出了基于似然比方法的法庭证据评价方法[6]。 该方法首先在DNA 检验中得到了成功应用,随着研究和技术方法的不断深入,法庭科学的很多分支领域也开始运用该技术方法。 基于似然比方法进行特征价值的量化评估、验证测试以及案件检验的实证研究,更好地推动了该方法的实践应用。 2015 年,欧洲法庭科学研究所联盟(European Network of Forensic Science Institutes, ENFSI)还发布了基于似然比方法的法庭证据评价报告指南[7],用于指导、规范该技术方法的实践操作。 目前,似然比方法在国外法庭科学领域取得了丰富的研究成果和广泛的实践应用。 在国内,除了DNA 领域以外,该技术在语音、图像等领域的研究成果相对较多[8],在痕迹检验领域的研究成果较少。

为了充分挖掘弹壳击针头痕迹三维立体特征数据价值、量化评估特征参数的有效性以及探索似然比方法在枪弹痕迹检验中应用的可行性,本文以两类枪支为代表,对其射击的样本弹壳进行三维特征数据测量,并采用似然比方法进行特征价值和有效性的量化评估。 这对于提高枪弹痕迹检验的科学性和客观性具有重要意义。

1 似然比方法

1.1 似然比含义及表达式

似然比(Likelihood Ratio,LR)是指同源假设条件下获得证据的概率与不同源假设条件下获得证据的概率之比[9]。 似然比方法属于一种逻辑框架,用于评价两种竞争假设条件下获得证据的可能性大小。 在法庭科学领域,一般应用于检材和样本的同源性比较。 同源假设又称起诉假设,不同源假设又称辩护假设。 因此,计算LR值可以量化评价证据支持控辩假设的程度,进而为法庭科学采信证据提供客观依据。

在枪弹痕迹检验中,比较典型的场景之一就是将现场遗留的检材弹壳与嫌疑枪支发射的样本弹壳进行比较鉴别,判断二者是否为同一支枪发射的。在这种场景下:

起诉假设Hso:检材弹壳与样本弹壳来自同一发射枪支。

辩护假设Hdo:检材弹壳与样本弹壳来自不同发射枪支。

似然比LR的计算表达式如下:

其中,P代表“概率(Probalility)”,E代表“证据(Evidence)”,即检材弹壳与样本弹壳的特征。P(E|Hso)表示同源假设条件下获得证据的概率,P(E|HDo)表示不同源假设条件下获得证据的概率。LR的分子代表检材与样本的相似性,LR的分母代表检材与样本特征在相关背景枪支中的典型性。 而典型性的评估需要一定规模的相关枪支的数据库支撑[10-11]。

此外,枪弹痕迹检验中,还有另外一种典型场景,即嫌疑枪支有两种(或两支),这时候需要将检材弹壳与两种(或两支)嫌疑枪支发射的样本弹壳进行比较鉴别,判断检材弹壳是两种(或两支)枪支中的哪一类(或哪一支)发射的。 在这种场景下,相关背景枪支仅为一种(或一支),样本及特征采集和数据分析就简单很多。 特征提取、数据测量以及LR计算只需针对这两种(或两支)枪支发射的弹壳痕迹即可。

起诉假设HA:检材弹壳与样本弹壳来自A(类)发射枪支。

辩护假设HB:检材弹壳与样本弹壳来自B(类)发射枪支。

似然比LR 的计算表达式为:

LR用来评价两种竞争假设条件下获得检材弹壳和样本弹壳痕迹特征的可能性大小。 在似然比框架下,LR大于1,表明证据支持起诉假设;LR小于1,表明证据支持辩护假设;LR等于1 表明证据支持起诉假设和支持辩护假设的程度相等,因此没有价值。LR越大于1 或越小于1,证据支持假设的程度越大,因此越有价值。

本研究基于第二种场景,对两种枪发射的弹壳的击针头痕迹三维特征进行似然比方法研究,一方面探索该方法在枪弹痕迹检验中的可行性,另一方面通过该方法量化评估击针头三维痕迹的特征价值。

1.2 特征提取、统计模型和似然比计算

基于似然比方法的分析检验是建立在特征数据基础上的。 在弹壳痕迹检验中,需要对检材弹壳痕迹、样本弹壳痕迹以及相关背景枪支的样本弹壳痕迹进行特征的量化提取。 提取的特征数据还要进行统计模型构建和LR 计算。 不同类型的数据需要构建合适的计算模型。 第一种场景下,常用的针对多维数据的LR 模型为多变量核密度(KVKD) 模型[12],而对于本研究中第二种场景下的两分类问题,线性判别分析(Linear Discriminant Analysis,LDA)和逻辑回归(Logistic regression,LR)方法是更合适的选择。 由于逻辑回归方法不依赖于数据的高斯分布假设,因此在不能确保数据的正态分布时,逻辑回归方法比线性判别分析更有效[13]。

采用逻辑回归模型进行似然比计算,既适用于一维特征向量(一个特征参数),也适用于多维特征向量(多个特征参数融合)[14]。 在本研究中,其一维特征向量和二维特征向量的LR 计算表达式分别为(3)和(4):

在这两个线性方程中,X代表一维特征向量,X1和X2分别代表二维特征向量中的第一个特征向量和第二个特征向量,a 为截距,b 和c 为斜率。 a、b、c 的值需要由一定规模的、相关弹壳击针头痕迹的测量数据计算得到。 逻辑回归是一种分类模型,它基于贝叶斯定理,通过计算后验概率的大小进行两分类的判别。 按照贝叶斯定理,后验概率=先验概率×似然比。 使用逻辑回归模型计算似然比时,由于对训练数据中的两类数据点赋予了相同的权重,因此先验概率为1。 此时,后验概率就等于似然比。

1.3 系统验证和性能评价

为了验证痕迹特征及其统计模型的有效性,基于似然比方法的检验需要进行“系统”的验证测试。“系统”是个统称,每个特征及其统计模型都可以称之为一个“系统”。 只有在系统的准确性和可靠性满足法庭要求时,才能应用于实际案件的检验。 因此,系统验证是基于似然比方法的法庭证据评价的标准步骤,也是其科学性和优越性的体现。

系统验证一般基于已知真实答案的数据库进行,即数据库中每个样本来源于哪个发射枪支是已知的。 利用提取的特征进行所有样本的交叉比较,然后计算每次比较的LR值。 理想条件下,如果两个样本来源于同一(类)枪支,其LR值应该大于1;如果两个样本来源于不同(类)枪支,其LR值应该小于1。 如果LR值的结果与数据的事实来源不符,则等于判别错误。 因此,将系统判别的结果与真实答案进行比较,统计其评价指标,就可以量化评估系统的性能。

基于LR 方法的系统验证评价指标有:

(1)对数似然比代价函数

对数似然比代价函数(Log likelihood ratio cost,Cllr)[15]是似然比证据评价体系下进行系统验证的标准评价指标,其表达式如公式(5)所示。

其中,Ns和Nd分别是同源和不同源测试对的数量,LRs和LRd分别是同源和不同源测试对比较的LR值。 等式右边由两部分组成,第一部分代表同源样本自身比较的识别性能,第二部分代表不同源样本之间比较的识别性能。Cllr值衡量的是系统的整体表现,Cllr值小于1 表明系统有效,Cllr值越小,系统的识别性能越好。

(2)等误率

等误率(Equal Error Rate,EER)是自动识别中常用的性能测试指标。 在系统识别过程中,出现错误识别的情况有两种:一是将不同来源的数据错判为同源,即错误接受;二是将相同来源的数据错判为不同源,即错误拒绝。 错误接受率(False Acceptance Rate,FAR) 和错误拒绝率(False Rejection Rate,FRR)相等时的概率就是等误率。 系统的等误率越小,识别越准确。

(3)Tippett 图

Tippett 图(可靠性函数图)是基于似然比框架方法的系统验证测试的标准图示表达。 Tippett 图的横轴是以10 为底的对数似然比(log10LR),纵轴是LR 值的概率累计分布。 Tippett 图中,向右上延伸的曲线代表同源数据之间的比较,向左上延伸的曲线代表不同源数据之间的比较,两条曲线的交叉点对应的概率代表等误率(EER)。 两条曲线分得越开,交叉点越低,系统识别的效果也就越好。

2 实验方法

2.1 样本收集

选取9 mm 警用转轮手枪和QSZ92 手枪各5把。 每种手枪分别进行100 次射击,从收集的射击弹壳中随机抽取两类样本弹壳各50 枚,得到两种手枪射击的样本弹壳总计100 枚。 将挑选出来的样本弹壳贴上自粘性便签纸并依次从1 ～50 编号,如图1 所示。

图1 部分实验样本弹壳

2.2 测量方法

本研究使用的测量仪器是日本生产的KEYENCE 超景深三维立体显微镜,型号为VHX-1000C,如图2 所示。 分别对上述弹壳样本进行击针头痕迹的三维立体数据采集和体积、表面积测量,测量精度为μm 级。 测量时将超景深三维立体显微镜放置在水平桌面,并通过水平仪校准。 将弹壳放置于载物台上,调节显微镜物距,使其聚焦于击针头痕迹,通过控制板的“深度合成/3D”和对焦调整功能,对击针头痕迹分层进行调焦拍摄,融合成击针头痕迹的3D 图像,而后基于合成的击针头痕迹3D 图像,进行立体痕迹参数测量。

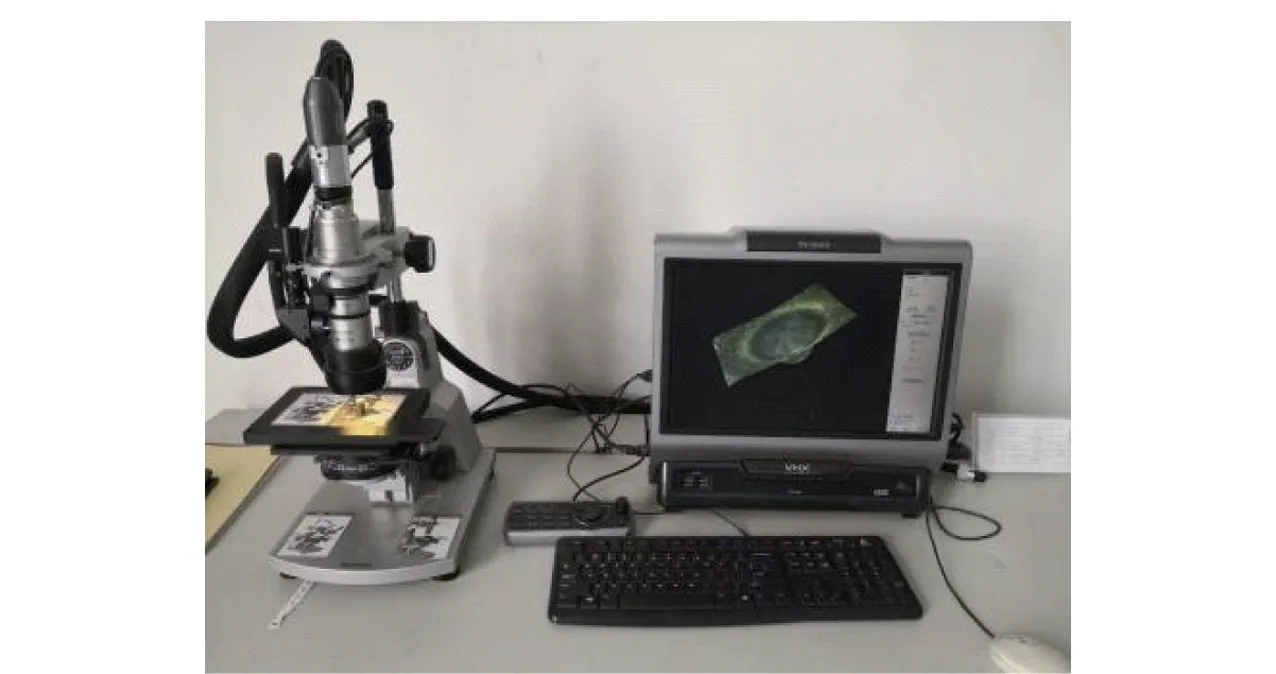
图2 超景深三维立体显微镜

本研究测量的立体痕迹参数为击针头痕迹的体积和表面积,如图3 所示,图3(a)、图3(b)为9 mm转轮手枪弹击针头痕迹,图3(c)、图3(d)为92 式手枪弹击针头痕迹。 对100 枚弹壳依次测量,每枚弹壳测量4 次,每次测量均使弹壳自转90°,然后取4 次测量数据的平均值,并记录体积和表面积数据。为了降低测量误差,需要将调整好的观测系统加以固定,以保证每枚弹壳测试条件的一致性,部分实验数据如表1 和表2 所示。

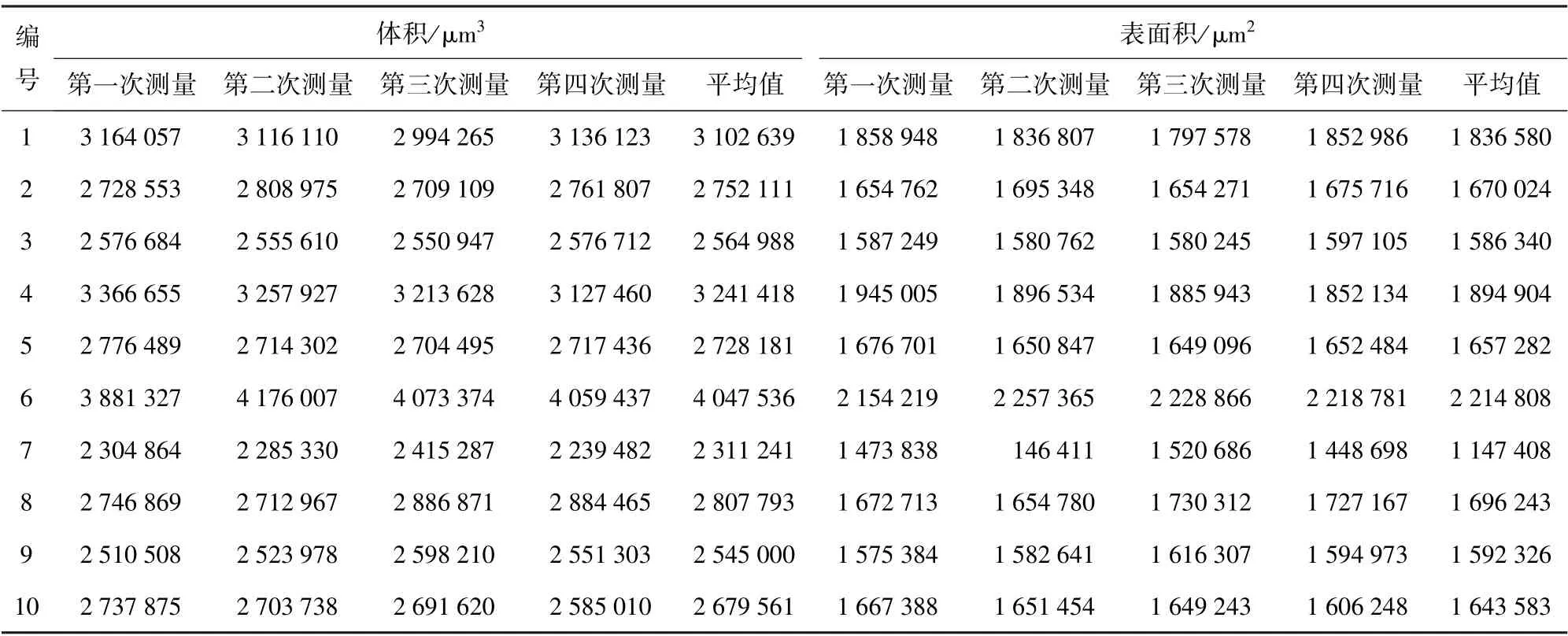
表1 9 mm 转轮手枪弹击针头痕迹部分实验数据

表2 QSZ92 式手枪弹击针头痕迹部分实验数据

图3 击针头痕迹的体积和表面积测量

2.3 统计处理

本研究中,参数特征的统计处理、验证测试的交叉比较、似然比的计算以及性能指标的计算均是基于MATLAB 程序脚本进行。

3 结果与讨论

3.1 击针头痕迹体积和表面积的数据分布

对两种枪支发射弹壳的击针头痕迹的体积和表面积数据进行初步统计分析,结果见表3。 其中,A代表9 mm 警用转轮手枪,B 代表QSZ92 式手枪。

表3 击针头痕迹体积和表面积的数据统计

从表3 中的数据可以看出,两类枪支的弹壳击针头痕迹的体积数据和表面积数据的标准差和极差较小,数据本身具有类内规律性和较好的稳定性,说明数据的量化提取方法是准确可靠的。 同时,这两种特征数据又具有一定程度的类间重叠交叉性,这是由大多数连续变量的数据属性决定的。

为了进一步探究这些数据的分布规律和特点,本研究对体积和表面积两个特征参数进行了概率密度分布统计,结果见图4 和图5。

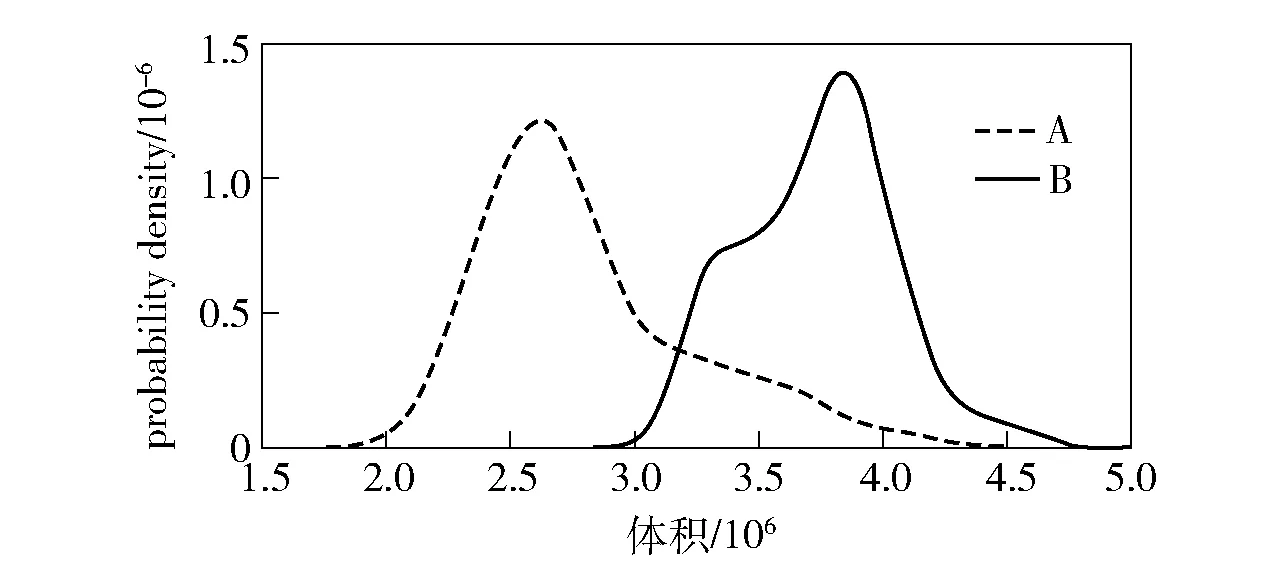
图4 两类枪支发射弹壳的击针头痕迹体积的概率密度分布

图5 两类枪支发射弹壳的击针头痕迹表面积的概率密度分布

图4 的横轴为两类枪支发射弹壳的击针头痕迹的体积,图5 的横轴为两类枪支发射弹壳的击针头痕迹的表面积,两图的纵轴均为横轴特征参数的概率密度。 从这两个特征参数的概率密度分布来看,A 类枪支发射弹壳的击针头痕迹体积和表面积均呈近似正态分布,而B 类枪支发射弹壳的击针头痕迹体积和表面积均略呈双峰分布。 此外,两类枪支发射弹壳的击针头痕迹的体积和表面积数据存在一定程度的交叠。 对于这种特征值存在交叠情况的数据来说,仅依据参数特征的数值大小和设定的阈限进行直接判断,非常容易出现错误。 而如果仅考虑非交叠部分进行阈值判断,则交叠部分的数据就失去了利用价值。 而事实上,交叠分布的特征参数,也具有区分价值。 对于这种类型的特征数据,用似然比方法是最合适的。 似然比方法不仅可以用于基于概率评价的枪支区分,还可以基于所选特征参数进行测试验证,量化比较和评价特征的有效性。

3.2 单一特征系统的验证测试

利用上述击针头痕迹的全部体积数据和表面积数据,分别进行“留一法(leave-one-out)”交叉验证测试。 即每次抽取一个特征数据作为特征向量进行测试,用剩下的49 个特征数据进行逻辑回归模型训练,然后计算该特征向量的LR值。 这样,依次抽取每个特征数据进行LR计算,直到50 个数据全部抽取完。 最后,分别得到来自两类枪支发射弹壳击针头痕迹体积特征的LR值、表面积特征的LR值以及二者融合特征的LR值。 根据各组的LR值结果,分别计算两个单一特征系统和一个融合特征系统的性能指标Cllr值和EER 值,并输出各自的Tippett 图。

两个单一特征系统及其融合特征系统验证测试指标的数值结果,见表4。

表4 两种特征参数验证测试的Cllr值和EER 值

从表4 中的性能评价指标来看,两个单一特征系统测试的Cllr值在0.35 ～0.45 之间,EER 值在12% ～16%之间,说明两个特征参数均具有一定的识别能力和区分价值。 整体上,利用体积和表面积单一特征参数进行判别的效果近似,错识率都较低。但比较而言,击针头痕迹表面积的特征价值要更高一些,区分效果要更好一些。

两个单一特征系统及其融合特征系统验证测试的图示结果,见图6 ～8。 其中,图6 是利用体积特征数据得到的Tippett 图,图7 是利用表面积特征数据得到的Tippett 图,图8 是利用体积和表面积的融合特征数据得到的Tippett 图。

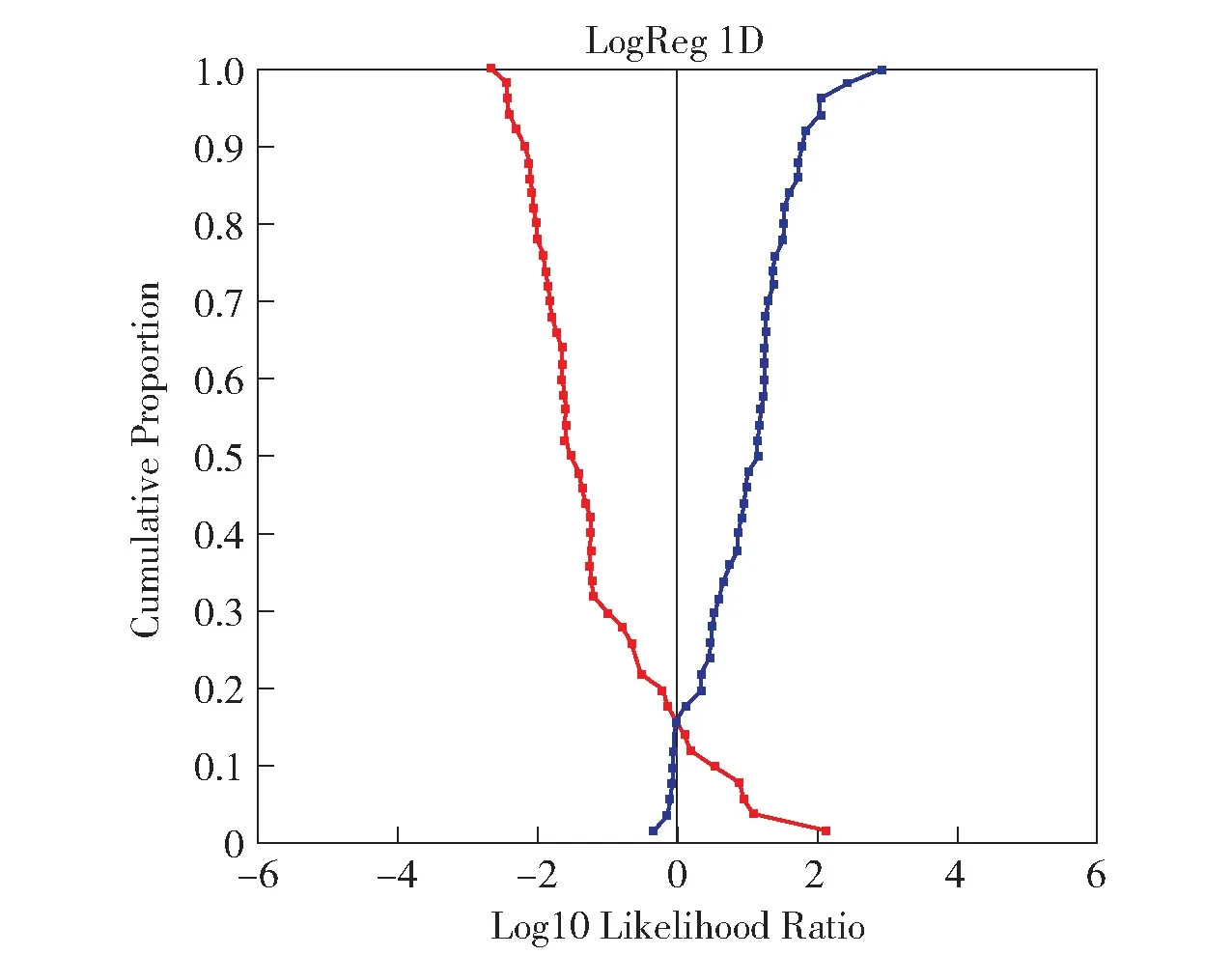
图6 利用击针头痕迹体积特征数据进行系统验证测试的Tippett 图

图7 利用击针头痕迹表面积特征数据进行系统验证测试的Tippett 图

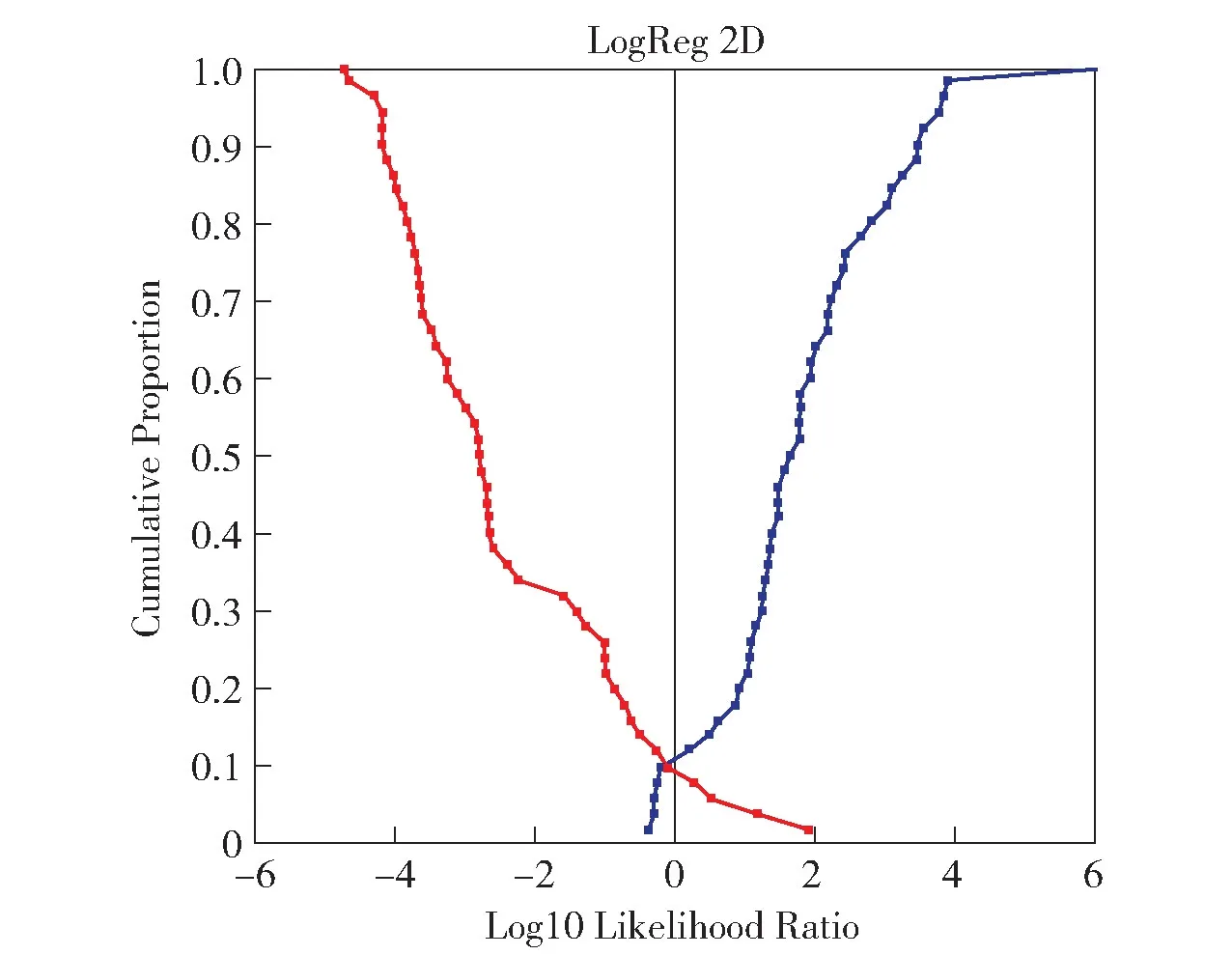
图8 利用击针头痕迹体积和表面积融合特征数据进行系统验证测试的Tippett 图

这里,Tippett 图代表的是根据已知来自A 类枪支弹壳击针头痕迹的特征测试数据和已知来自B类枪支弹壳击针头痕迹的特征测试数据得到的所有LR值的累积分布。 对于图中向右上升的曲线来说,其纵轴数值代表的是来自A 类枪支特征数据的LR值等于或小于横轴数值的比例;对于向左上升的曲线来说,其纵轴数值代表的是来自B 类枪支特征数据的LR值等于或大于横轴数值的比例。 图中的圆点代表每个特征向量计算的对应结果。

从曲线分布的情况来看,图6 和图7 中的两条曲线都分得比较开,两条曲线的交叉点也比较低,说明与数据来源事实相反的LR值占比较低。 同样,比较而言,击针头痕迹表面积特征数据的区分效果要好于体积特征数据,因为其Tippett 图中两条曲线的倾斜更为平缓、分得更开、交叉点也更低。

3.3 两个特征融合系统的验证测试

通过表4 中的性能评价指标比较,可以清楚地看到体积和表面积的融合特征系统的性能明显好于两个单一特征系统。 融合系统的Cllr值为0.279,分别比体积特征系统和表面积特征系统的Cllr值下降了35%和27%。 这充分说明两个特征的融合判别是有效的,而表面积特征对判别的贡献更大。 EER值的结果也是如此。 与图6 和图7 的单一特征系统相比,图8 中两个特征的融合系统的两条曲线分得更开,说明区分效果更好。 两条曲线的倾斜程度也更加平缓,说明与事实相符的LR值的数量级更大,数据对正确判别结果的支持力度更大。

4 结论

本文采用超景深三维立体显微镜,对两类枪支发射的多枚弹壳击针头痕迹的体积和表面积进行了3D 数据测量,对两个特征参数的数据分布特点进行了分析。 在此基础上,基于似然比方法,分别利用这两个特征数据进行了两类枪区分的验证测试。 研究结果表明:这两类枪支发射弹壳的击针头痕迹体积数据和表面积数据均存在一定程度的交叉,因此利用交叉区域的数据进行枪支判别存在明显的不确定性。 在法庭科学中,很多痕迹特征的测量数据都属于连续变量,并具有这种交叉分布的特点。 对于这种无法截然分开的数据来说,不管是进行数据来源的种类推断,还是进行数据来源的个体推断,基于LR 方法和统计模型进行来源判别的概率评估都是合理的选择。 本研究也表明利用3D 光学测量技术对弹壳击针头痕迹进行三维特征数据的量化提取方法准确有效,利用该技术提取的体积特征数据和表面积特征数据都具有较好的枪支区分价值和区分能力。 比较而言,表面积特征的区分效果更高,而两个特征融合的区分效果最好,这进一步验证了多维特征向量的更强判别能力和更高证据价值。 可见,基于LR 方法的枪弹痕迹检验完全可行,值得推广。LR 方法属于一种框架体系,适用于所有可以进行量化测量的痕迹检验和同源性鉴定。 该方法不仅可以量化评价特征数据的有效性和证据价值,还可以量化评价检验系统或检验方法的准确性,为法庭提供客观量化的检验结果和鉴定依据,进而提升检验的科学性和客观性。