测量透明微粒群参量
2022-10-17曾永顺刘家泽李汶俊高春萍郭宸珲吴泳波唐志列
曾永顺,刘家泽,李汶俊,高春萍,郭宸珲,吴泳波,唐志列
(华南师范大学 物理与电信工程学院 物理国家级实验教学示范中心,广东 广州 510006)
固液体微小颗粒广泛存在于日常生活和工业生产中,其粒径分布及折射率的准确测量直接关系到产品质量[1]及能源消耗[2]等,因此对颗粒粒径分布及折射率的准确测量有重要的研究意义和价值.
在测量方法中,光学方法由于其非接触的特点在近年来得到广泛运用. 激光衍射法[3]通过扩束和滤波产生单色平行光,平行光穿过颗粒群后的衍射信号包含颗粒群的尺寸分布、折射率等参量. 全息技术[4]采用激光照射颗粒群并用相机记录全息信号,对全息图数字再现后提取粒子的参量信息,实现颗粒尺寸分布的测量. 显微镜法[5]利用光学或电子显微镜观测粒子的形貌并测定其大小,可实现对纳米粒子的测量,但测量效率较低. 动态光散射技术[6]又称为光子相关光谱技术,研究颗粒布朗运动导致的散射光波动现象,使用数据处理方法从一定角度下随时间变化的散射光的波动信号中反演粒径及分布.
综上,光学方法在颗粒测量方面应用广泛,但仍然存在一定的局限性:部分方法无法同时测量固液颗粒的多个参量,例如显微镜法只能测量颗粒的粒径但无法测量其折射率;还有部分方法对设备要求较高,例如离轴全息和动态光散射技术.
在光散射现象中,平行光束照射透明颗粒群时,在后向散射区1阶彩虹角附近形成干涉条纹,干涉条纹中包含透明颗粒群参量的信息. 本文设计了简单的测量系统,利用Nussenzveig理论和改进的量子粒子群算法反演粒径分布和折射率. 以粒径范围为400~600 μm的玻璃微珠群作为样品,并对测量误差进行分析;再对不同浓度乙醇溶液喷雾的折射率进行测量,分析其与文献值的误差. 结果表明,本方法能够实现对透明颗粒群的粒径分布和折射率的快速实时在线测量.
1 反演方法
1.1 理论
基于几何光学理论[7]的模型图如图1所示,展示了平行光照射球形截面时的光线.p表示光线与透明微粒内表面相互作用的次数,p=2表示与微粒内表面发生1次反射后出射的光线,这类光线是本文的主要研究对象,其所对应的散射角被称为几何彩虹角或1阶彩虹角.

图1 透明球形微粒截面处的光路图
Airy理论[8]、Lorenz-Mie理论[9]和Nussenzveig理论[10]是常用的几种描述透明球形颗粒的后向散射区1阶彩虹角附近光强分布的理论. Airy理论利用波动光学理论对彩虹角附近的光强进行求解,是近似解. Lorenz-Mie理论从电磁场出发,给出了均匀介质球被平面电磁波散射的精确解,但其解由无穷序列求和构成. Nussenzveig理论引入各种近似解析取代了Lorenz-Mie理论中无穷级数的计算过程. 本实验将综合考虑准确性和计算速度以选择使用的理论. 在实验中主要使用2种材料,分别为水滴和玻璃微珠,并以单个玻璃微珠为例进行计算. 取折射率m=1.510 0,粒径d=500 μm,激光入射波长λ=648 nm,绘制Airy理论、Lorenz-Mie理论和Nussenzveig理论在彩虹角附近的光强,如图2所示.

图2 3种理论的对比
Nussenzveig理论关于p的表述与几何光学相同,p=2表示只考虑经过1次内表面反射的折射光,p=0,2表示在p=2的基础上增加考虑颗粒外表面反射光,p=0和经过1次内表面反射的折射光p=2间的相互干涉. 对比3种理论,Lorenz-Mie理论计算速度明显偏慢,Airy理论则有所偏移,Nussenzveig理论在p=0,2光强上与Lorenz-Mie理论有一定偏差,但p=2部分符合Lorenz-Mie理论的低频部分. 因此,Lorenz-Mie理论适用于对单个颗粒的散射光强的计算. 对微粒群,多个透明微粒叠加信号中高频信号相互抵消,叠加信号为低频信号,从算法速度和实验误差上考虑,选择将Nussenzveig理论p=2的散射光光强用于微粒群中单个微粒的光强.
1.2 粒径分布和折射率反演模型
根据对单个颗粒彩虹角附近光强分布特性的研究可知[11],颗粒的粒径决定了干涉信号峰与峰之间的散射角间隔,颗粒的折射率决定了干涉信号主峰所在的散射角位置,因此,通过拍摄干涉图像,提取干涉信号前2个干涉峰信息,用干涉峰信息与Lorenz-Mie理论对比可以实现对单个颗粒粒径和折射率的反演计算.
已有理论均为对单微粒散射光强的解释,为了实现对微粒群在测量区域平均折射率和粒径分布的测量,需要对微粒群在彩虹角附近的光强分布建立模型. 假设如下:a.不考虑颗粒间的复散射现象,即彩虹角附近的光强只考虑入射光对各个微粒散射光强的叠加;b.在同一散射角上,各个颗粒产生的散射光可以线性叠加;c.假设微小测量区域内微粒群具有相同折射率. 由此颗粒群在测量区域产生的光强为
(1)
其中,I(di,m,θ)为在单个折射率为m、粒径为di的球形颗粒按Nussenzveig理论在散射角为θ下的光强,N(di)为粒径为di的颗粒个数,不同粒径的粒子i共有n′个.在本模型中,微粒群的粒径分布有高斯分布和对数高斯分布2种假设,μ和μl,σ和σl分别为高斯和对数高斯分布的均值与标准差,利用均值与标准差生成符合对应分布的粒径随机数公式为:
di=σ·randn()+μ,
(2)
(3)
其中,randn()为Matlab中产生服从标准高斯分布随机数的函数,利用式(2)得到符合高斯分布的粒径随机数. 利用Matlab中lognrnd函数得到满足对数高斯分布的粒径随机数[式(3)].
在测量方法上,建立目标函数用于描述拍摄的真实光强与反演的理论光强间的重合程度,将误差平方和作为准则,目标函数如下:
(4)
其中,Icap为相机拍摄的光强信号,Ire为微粒群的理论光强信号,同样也作为反演光强.为了提高算法反演速度,将连续的光强分布信号离散化,k为离散点的序号,n为离散点总数.
计算过程中,选定假设的粒径分布后,微粒群的折射率m,粒径分布的均值μ和标准差σ为决策变量.利用算法控制m,μ和σ,从而调控反演光强Ire寻找目标函数最优值,最优值所对应的折射率m与粒径分布即为测量值.
1.3 改进的量子粒子群算法
在算法的选取上,群智能优化算法的强鲁棒性体现在分布式控制下,个体故障不会影响整体问题的求解;对于微粒群彩虹角附近的光强信号,每个微粒的位置随机分布,并且当微粒群中存在部分非球型微粒时也不会影响原本彩虹角附近光强的基本特征. 由于群智能算法的基本特征与微粒群彩虹角附近光强信号的相似性,在技术上使用量子粒子群优化算法[12]作为微粒群彩虹角附近光强信号的粒径分布反演算法是可行的.
受遗传算法交叉操作的启发,改进的量子粒子群优化算法增加对每一维度进行交叉的步骤,如果某一维度得到进化,则立即更新粒子的历史最优,下一维度的交叉可以迅速得到这一维度更新的有利反馈[13].
基本过程如下:初始化时,每个粒子都携带有折射率m,均值μ和标准差σ的信息,将新产生的粒子的每一维分别代入个体最优位置pbest和种群全局最优位置的gbest相应维度,并进行目标函数值的比较,如果优于先前结果,则更新pbest和gbest. 经过对各粒子的解向量逐维比较,能够使粒子向目标最优位置“快速前进”,尽快进入局部搜索,改进后的算法步骤如图3所示.
1.4 数值模拟
在理论层面,实验误差来源于2方面:a.Nussenzveig理论与真实光强分布即Lorenz-Mie理论的误差;b.算法误差. 对折射率、粒径大小的测量依赖于理论和算法的准确性,为了验证该方法的可靠性,用模拟光强信号进行验证. 用计算机生成m=1.333 0,μ=150 μm,σ=20 μm的高斯分布的透明颗粒群,利用Lorenz-Mie理论计算单个微粒在1阶彩虹角附近的散射光强,叠加得到模拟光强分布. 假设N(di)服从高斯分布,利用Nussenzveig理论和改进的量子粒子群算法计算模拟信号,取最大迭代次数为50,计算得到折射率m=1.332 7,相对偏差为0.02%,粒径分布符合高斯分布,μ=140 μm,σ=24 μm. 模拟信号和反演信号拟合结果、粒径分布和收敛过程见图4,其中f为频次,F为目标函数的最优值/最小值,N为迭代次数.
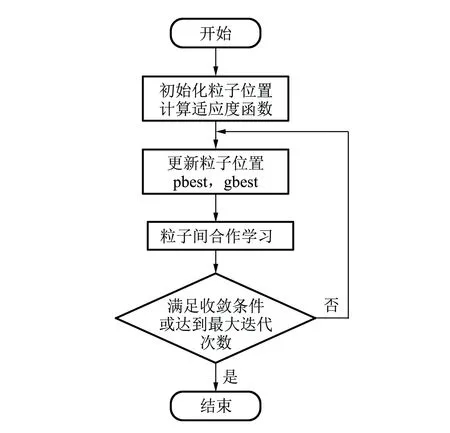
图3 改进后的量子粒子群优化算法计算流程

(a)拟合结果
2 实验装置与内容
2.1 测量系统的搭建
测量系统包含激光发射部分和信号接收部分,如图5所示.

图5 测量光路
激光发射部分为调整好入射角度的单色半导体激光器(λ=648 nm). 信号接收部分是由收集透镜、成像透镜、小孔光阑和面阵CCD组成,本实验中使用2个透镜(D1=D2=67 mm)、孔径可调的小孔光阑和面阵CCD. 透镜1为收集透镜,收集透镜的作用是收集颗粒群在光学彩虹角附近的散射光信号,收集透镜将测量区域内各个透明颗粒向不同角度发出的散射光会聚在收集透镜的焦平面上,即被光束照射的多个微粒在同一散射角下的散射光经收集透镜会聚在焦平面上的1点. 非焦平面位置不同散射角的散射光会重合,使图像失真. 透镜2作为成像透镜,将透镜1焦平面成像在CCD感光面上,小孔光阑的目的是滤去背景光并控制测量区域的大小.
2.2 散射角标定
测量系统中采用CCD相机接收1阶彩虹角附近的光强信号,需要对散射角进行标定,找到CCD相机所得图像的像素与散射角之间的对应关系.
反射镜标定法[14]是比较成熟、构造比较简单、在光学测量技术中经常采用的标定方法. 反射镜标定光路如图6所示,在原有测量光路的基础上,增加绿色激光(λ=532 nm)用于确定测量位置. 使原有测量位置处于反射镜中心,用精密旋转台旋转反射镜,依次调节旋转角度,记录下每1次精密旋转台的读数与光斑在CCD上的相应像素位置,由几何关系得到散射角,通过与像素点进行线性拟合,可以得到散射角与CCD像素的关系为
θ=0.004 3x+152.1
,
(5)
其中,θ为平面镜反射镜(即散射角),x为照片像素点的坐标.
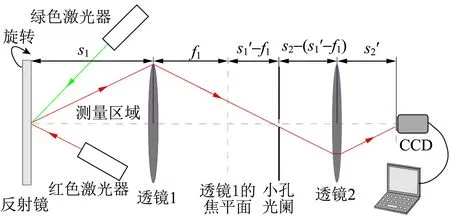
图6 标定光路
3 实验结果
3.1 玻璃微珠群的测量
使用粒径分布范围为400~600 μm的玻璃微珠群作为样品,并采用漏斗在测量区域形成玻璃微珠群,利用高速相机记录微珠群产生的光强信号,实验结果如图7所示,该图为拍摄到的颗粒群叠加信号,多个颗粒在1阶彩虹角附近的光强相互叠加,使得干涉条纹变得平滑,得到光滑的干涉信号.

图7 玻璃微珠群产生的干涉信号
为提高计算精度,截取干涉信号前2个峰用于反演;为了进一步降低环境噪音影响,取干涉图中心200行像素取平均作为实验光强信号. 采用QPSO假设粒径服从高斯分布,并对实验光强进行反演,设置迭代次数为50,反演结果如图8所示. 反演目标函数值Fgbest小于0.1,m=1.522,高斯分布的粒径参量为μ=514 μm,σ=39 μm,均值与参考值500 μm的相对偏差为2.8%,且粒径均处于400~600 μm范围内.
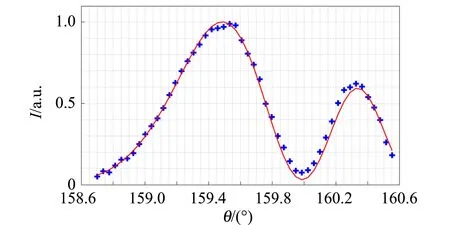
(a)拟合结果
3.2 液滴群的测量
在测量系统中采用喷雾喷头产生液滴群,包括水与不同体积分数的乙醇溶液. 对液滴群在1阶彩虹角附近的干涉条纹(又称作1阶彩虹)进行测量,需要重新使用反射镜标定法进行标定,液滴群测量的标定方程为
θ=0.004 4x+133.107
(6)
液滴群干涉条纹如图9所示,采用同样的图片处理方法,假设液滴群粒径服从对数高斯分布,使用量子粒子群优化算法分别对水与乙醇产生的液滴群进行反演,迭代次数为50次,水溶液反演结果如图10所示,目标函数值Fgbest小于0.2,m=1.327 1,粒径分布在30~120 μm之间,大部分分布在70 μm附近,体积分数为15%的乙醇溶液反演结果如图11所示,测量得折射率m=1.337 7.

图9 液滴群产生的1阶彩虹

(a)

(a)拟合结果
图12为体积分数φ=0,15%,33%,75%的乙醇溶液作为液滴群产生的1阶彩虹信号,表1为所测得不同体积分数乙醇的折射率m,并将其与已有文献值[15]结果进行比较,测量值随乙醇体积分数增大而偏小,是由于乙醇挥发导致,相对偏差均小于0.7%.

图12 不同体积分数的乙醇溶液产生的1阶彩虹信号
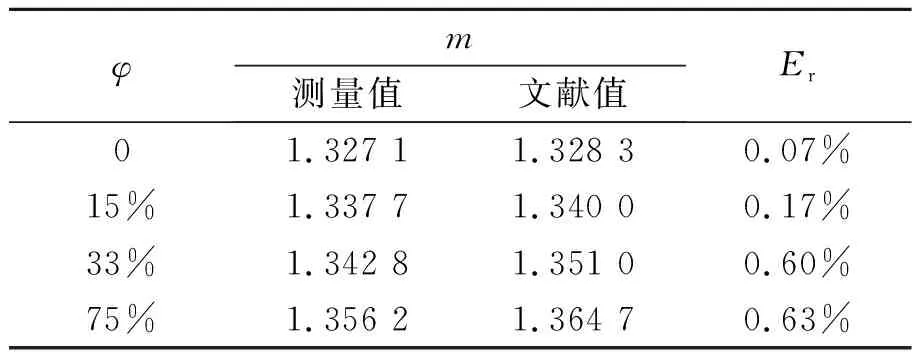
表1 乙醇的折射率
4 结 论
本文利用透明微粒群在后向散射区1阶彩虹角附近的光强分布对其粒径与折射率进行测量. 对比了Airy理论、Lorenz-Mie理论和Nussenzveig理论在玻璃珠1阶彩虹角位置的光强分布,Nussenzveig理论p=2的散射光光强最适合用于反演. 建立了以拟合误差平方和最小的粒径和折射率反演模型;在数值模拟上,以Lorenz-Mie理论模拟透明微粒群的光强信号,反演结果准确性较高;在实验上,设计了简单的测量系统记录透明颗粒群在1阶彩虹角附近的光强信号,使用反演算法对透明颗粒群粒径分布和折射率测量,适用于粒径为5~2 000 μm的颗粒. 对玻璃微珠群的粒径测量表明,设计的测量系统和反演算法能准确测量粒径,均值相对偏差小于3%. 在不同体积分数乙醇的折射率测量中,相对偏差小于0.07%. 本方法能够同时实现对透明颗粒群粒径分布及折射率的快速测量.
