步进轮摆共振法测量流体黏度
2022-10-17郭泽贤沈凡皓包泽杭王子文陈水桥姚星星
郭泽贤,沈凡皓,包泽杭,王子文,陈水桥,姚星星
(浙江大学 a.竺可桢学院;b.物理学院,浙江 杭州 310027)
流体黏度的测量在工业领域扮演着重要角色,已被广泛用于水利工程、管道运输等领域之中. 黏度测量方法很多,例如落球法、旋转法、毛细管法、阻尼振动法、杯式黏度计法、微流体并流法、多散斑光谱法等[1-4],其中,阻尼振动法是落球法结合振动来实现的. 本文结合单摆阻尼法与共振法,实现测量流体的黏度,即步进轮摆共振法测量流体黏度. 步进轮摆共振法需要先对流体中的单摆运动进行研究,然后再添加步进轮摆,即指单摆的结点在水平方向上做小幅度的简谐振动. 该体系可以类比成在简谐力驱动下的弹簧振子模型,从而可以观测到共振现象,并通过调节驱动频率,找到共振频率,使得摆球的水平位移振幅或者角度振幅达到最大. 本文分析了步进轮摆共振法测量流体黏度的原理,推导出实验计算公式,并利用步进轮摆共振法测量流体黏度,分析了流体黏度测量精度及其他影响.
1 基本原理
1.1 摆球运动原理
对于在流体中运动的摆球,以摆的顶端为参考系,摆球受到重力Fg、浮力FB、摆线张力T以及黏滞阻力FD的作用,非惯性系下还需引入惯性力Fi[5],其受力分析如图1所示.
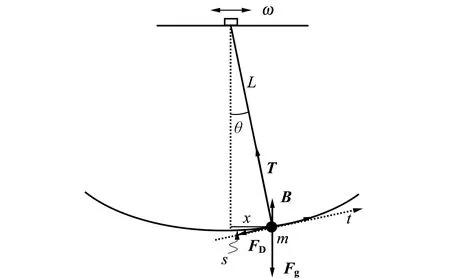
图1 摆球受力分析


FBsinθ-Fgsinθ-FD-Fi=ma,
(1)

(2)

(3)
1.2 步进轮摆运动原理
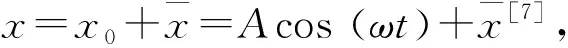
(4)
将式(4)代入式(3)可得:
(5)
1.3 流体黏度与共振频率的关系
(6)
联立式(5)和式(6),得到:
(7)
从式(7)的形式上看,小球摆的水平位移可视为受迫振动的弹簧振子,因此,式(7)可以改写成如下形式:
(8)

(9)
在摆幅最大时达到共振,所以有:

(10)
(11)
2 流体黏度简化公式
对于某温度下的待测液体,黏度固定,所以改变频率可以得到具体的位移振幅和角度振幅[8],即实验中可以测得相应频率的位移或角度.
计算机模拟单一黏度下水平位移振幅随驱动频率的变化曲线,如图2所示. 峰值从高到低的线分别对应0.1,0.2,…,0.7 Pa·s.

图2 单一黏度下水平位移振幅随驱动频率的变化曲线
通过位移振幅得到的模拟结果(图2)可以看出,黏度变化对共振频率的影响并不大,对黏度测量精度会有较小的误差,故实验采用测位移振幅的方法进行实验.
改变液体温度得到不同黏度下的共振频率,将不同黏度下的共振频率连线,结果如图3所示. 以上模拟均已考虑雷诺数修正以及容器壁修正[9,13]. 在三维图中可以清晰地看出共振频率随黏度的变化趋势.

图3 不同黏度下频率与振幅三维图
为探究不同模型修正对共振频率的具体影响,做不同黏度下的共振频率图,如图4所示.

图4 不同黏度下的共振频率图
3种模型中,模式1仅考虑了斯托克斯方程,模式2在模式1基础上加入了雷诺数修正,模式3在模式2基础上加入了容器壁修正. 经对比,发现黏度在0.3~1.1 Pa·s的范围内,可用线性表达式来表征黏度与共振频率的关系. 如图5所示,数值模拟结果的线性拟合R2=0.999 6,说明用线性公式代替繁琐的数值模拟是可行的.
黏度在一定的区间内, 模式3曲线与线性公式符合得较好,因此可以通过线性公式求出黏度测量值. 根据图5,得到的线性经验公式为
μ=-0.313ωm+1.844.
(12)
由上述分析可知,液体中做受迫振动的摆球,可以在特定情形下达到共振,测出共振频率即可得到液体黏度.
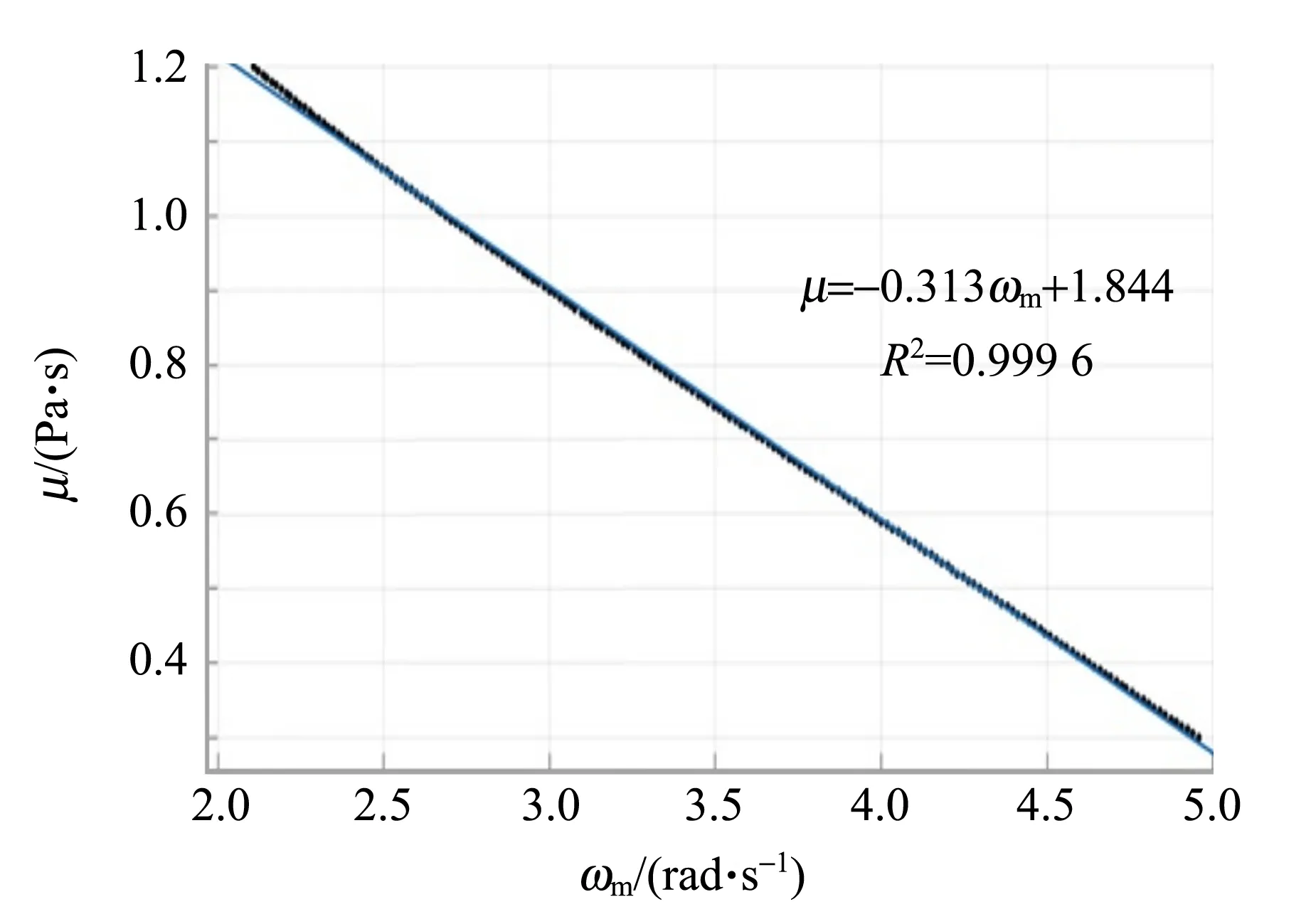
图5 将模拟所得数值解在一定区域内线性拟合
3 实验仪器
实验仪器由步进轮摆装置、共振频摆发生器、激光定位系统和数据采集与测量模块组成. 图6所示为实验仪器总框图.

图6 实验仪器总框图
3.1 步进轮摆装置
步进轮摆主要由步进轮摆车、滑轨和水平导轨组成,步进轮摆车包括水平杆、转框和四轮小车. 使用CAD构建模型,并利用3D打印,得到相应部件进行组装,将步进轮摆车置于滑轨上,并用水平泡调节滑轨水平. 将步进轮摆车上竖直维度传动框与转盘套合,使步进轮摆车仅可水平移动.
步进轮摆工作原理:转盘内的固定杆做匀速圆周运动,而水平导轨将该圆周运动投影在水平方向,从而推动步进轮摆车左右摆动,并带动摆球做简谐振动[10].
3.2 共振频摆发生器
共振频摆发生器主要由步进电机与转盘构成,步进电机输入信号由外接频率控制,从而控制转盘工作.
3.3 激光定位系统
激光定位系统由激光器和光电传感器组成,用来检测小球是否挡光,所以带量尺的光学导轨和激光定位系统可以实现小球最大摆幅测量[11]. 在本次实验的流体中,改变驱动频率后,小球迅速达到稳定,并做稳定的简谐振动,激光定位系统可精确记录小球摆动的左右水平极限位置(最大摆幅),反映水平位移的振幅大小,最终确定水平位移最大时对应的驱动频率大小,记录此值,即为该黏度下的共振频率.
3.4 数据采集与测量模块
数据采集模块使用Arduino开发板,程序设计主要思路如图7所示. 首先计算小球稳定平衡的弛豫时间ΔT,并得到稍大于弛豫时间的间隔时间. 通过按键控制模式参数mode,编写代码,使模式参数为auto(按下按键)和manual(松开按键)时分别对应自动模式和手动模式.
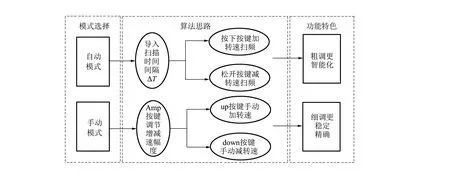
图7 数据采集与测量模块流程图
手动模式的算法主要利用了Arduino的并行输入接口,2个不同的输入接口分别对应增速和减速,还有1个输入接口对应增减速幅度的调节. 在实际实验中,可以先调节增减速幅度到达合适的数值,再按增速或减速按键调节转速,直至达到目标值.
自动模式的算法主要利用了Arduino内置的定时模块,设定间隔时间后,借助Arduino版的高刷新率性质, 可以定义条件语块,使得时隔后的时刻可以精确地提升或降低特定的转速. 此时按键功能变为控制变速的方向. 按下按键可以实现自动加转速扫频,松开按键可以实现自动减转速扫频.
功能特色在于可以更加智能化地进行测量或教学演示. 手动扫频与自动扫频可以自由选择. 手动扫频下,测量者可以更方便地找到已知的特殊频率值,并可以做更稳定的测量或演示. 自动模式下,设定的扫频间隔时间需稍大于小球的弛豫时间[14]. 打开Arduino开发板启动按键,步进轮摆的稳定振动频率会随着时间稳步改变,从而使测量者在调节过程中更加关注振幅测量.
4 实验结果与分析
通过测量不同黏度流体中运动的步进轮摆共振频率,进而实现黏度的测量以及不确定度分析. 通过更换摆长寻找精度最高的装置参量. 测量单一黏度下水平位移振幅与驱动频率之间的对应关系,并与理论结果进行比较,验证实验系统的可靠性.
4.1 实验数据与分析
摆长l=0.20 m时,10组不同黏度流体的黏度测量数据如表1所示,每种流体均进行了6次重复实验.
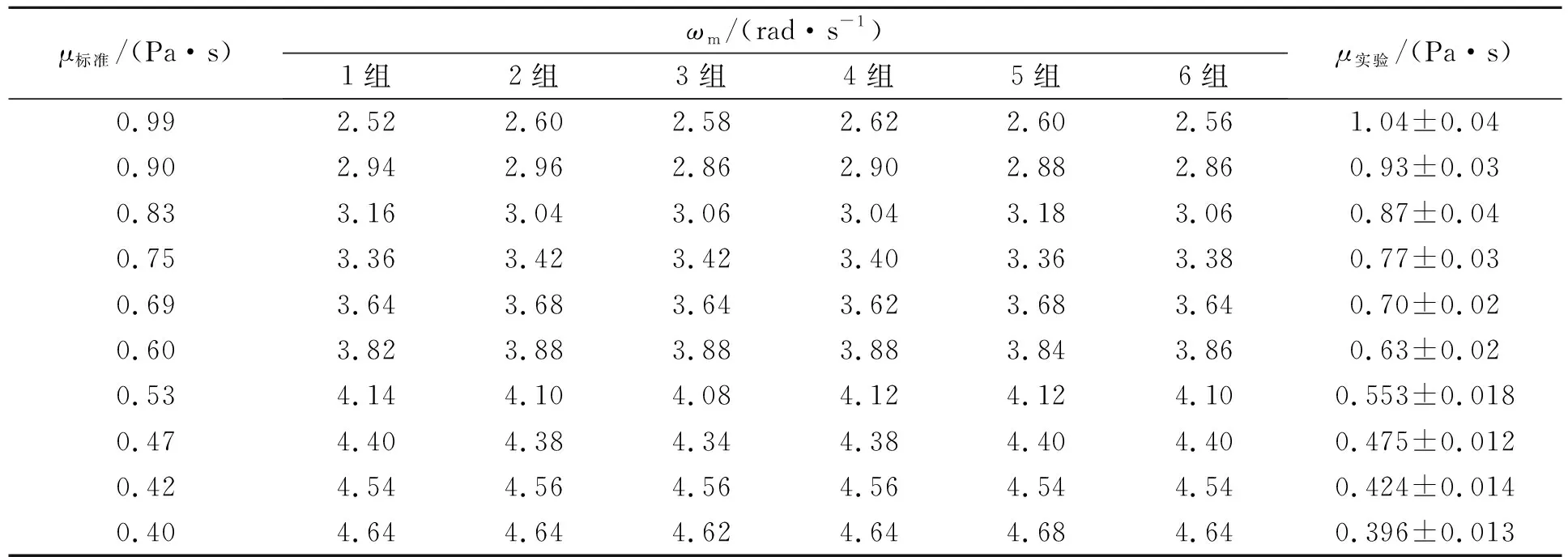
表1 不同黏度流体的黏度
根据表1数据,作测量值与标准值的分析图如图8所示. 从实验结果可以看出用线性公式拟合得到的黏度测量值与黏度标准值偏差较小,不确定度平均为±0.02 Pa·s,验证了实验系统的可靠性.

图8 实验测量值与标准值吻合度分析图
另外,由图8可知,黏度较大的流体相对来说误差较大,其原因是黏度较大时,共振峰较为平坦(品质因子Q值较低),共振频率的测量误差较大.
4.2 实验系统分析
4.2.1 摆长对黏度测量的影响
选取不同摆长l进行实验,得到黏度与共振频率的关系如图9所示.
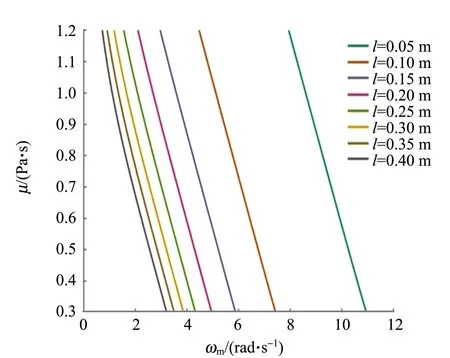
图9 不同摆长下黏度与共振频率的关系
摆长对流体黏度测量的影响主要是:要确保小球摆在振动过程中满足小幅振动的条件,即摆球摆动角度越小越不会产生较大误差.
4.2.2 温度对黏度测量的影响
在实验中改变液体的温度进行测量,结果如图10所示. 实验结果与理论符合较好,包络线误差为±0.02 Pa·s,拟合误差为±0.01 Pa·s.

(a)T=32.0 ℃
分析上述结果,发现在共振频率附近实验与理论曲线拟合较好,而在频率较低时整体实验数据偏大,这是由于此时轮摆振动幅度偏大,以及容器壁真实修正项与线性项存在较大偏离等因素所致. 在共振频率附近更为细致的扫频结果发现[图10(d)],相较于偏离共振频率附近的频率,实验得到的数据点与理论符合得更好.
4.2.3Q值对黏度测量的影响


图11 单一黏度下振幅随频率的变化
4.2.4 实验系统性能分析
1)测量范围
μmin=0.3 Pa·s,μmax=1.1 Pa·s.
2)测量精度
仪器精度为±0.02 Pa·s.最大黏度相对偏差为5%,最大黏度偏差值为0.04 Pa·s.
3)响应时间
改变频率至稳定振动所需时间小于2 s. 响应时间越快,达到稳定振动所需要的时间就越短,如图12所示,在1 s之后球摆就能达到稳定的简谐振动.

图12 小球位移随时间变化图
4.2.5 实验系统特点分析
1)与传统的单摆阻尼法测量黏度相比,此方法更加直观,同时能排除更多干扰因素,得到更精确的结果[15].
2)推导出一定黏度范围内,测量黏度的线性公式,避免了繁琐的计算.
3)用激光定位法观察和获取小球摆动的最大振幅,可以更直观地观察到黏度与驱动频率对振幅的影响,同时也使测量数据更加可信[16].
4)开发了摆动频率连续变化的搜索算法,用单片机控制驱动力频率,使实验者无需手动控制,装置更加智能.
5)本装置中,步进轮摆系统的构件全部采用3D打印技术实现,成本较低.
5 结束语
基于步进轮摆共振法的黏度测量方法,更适用于测量高黏度液体,并且在控制恒温的情况下可以得到精确测量. 通过计算机模拟,验证了在0.1~1.5 Pa·s的黏度范围内可有效地进行黏度测量,推导了在0.3~1.1 Pa·s的黏度范围内可用线性表达式表征黏度与共振频率的关系式,精度可达到0.02 Pa·s. 比较流体黏度的测量值与标准值,说明了用共振频率线性表征测量黏度的可行性. 实验系统还可以提高方法和措施:可进一步优化,做成集成的小型测量仪器或者手持式测量仪器;开发实时反馈共振频率的同时计算出相应黏度值大小并显示的系统;数据采集模块升级为采用束宽更细的激光进行振幅测量. 另外,如果以角度为自变量,也比较适合更小黏度流体的黏度测量,可以以此为方向做进一步探究.
