挖掘机动作协调性多指标综合评价方法

陈俊翔， 高春莹， 李 智， 吴 璇， 艾 超,2

(1.燕山大学 河北省重型机械流体动力传输与控制实验室， 河北 秦皇岛 066004；2.燕山大学 先进锻压成型技术与科学教育部重点实验室， 河北 秦皇岛 066004)

引言

挖掘机作为土石方工程的主要施工机械，在城市建设、矿产资源开采、水利电力工程等方面发挥着重要作用[1]。随着我国经济社会的发展和综合国力的增强，市场对挖掘机的需求量大大提升，并且对挖掘机的性能有了更高的要求[2]。评价挖掘机性能优劣的一个重要方面为执行机构动作的协调性。挖掘机作为具有多自由度的工程机械，在作业中需要多个执行机构同时进行工作，因此要求其具有良好的动作协调性。挖掘机在作业过程中出现的冲击、吸空、反应滞后等现象，对挖掘机的安全性和工作效率有很大影响。如何提升挖掘机动作协调性和如何精准评价挖掘机动作协调性，一直是行业研究的难点。

近年来，许多专家学者对挖掘机等产品进行过评价。刘敏等[3]曾应用灰色综合评判方法对液压挖掘机的性能进行评价，其采用专家咨询法直接确定各评价指标的权重系数，主观因素影响较大，导致指标评价值不准确且可信度较低。屈福政等[4]建立了灰色模糊优选模型，对于指标评价值的确定，其只建立了一种隶属函数，没有体现不同评价指标自身的特点，造成评价指标值不够精确。王卓等[5]采用模糊层次分析法对液力缓速器进行制动性能综合评价，对权重系数的计算较为客观，但其采用线性加法合成，存在评价值较高的指标补偿评价值较低的指标的现象。综上所述，在一个评价体系中，权重系数的处理、隶属函数的建立以及合成方法的选择会对最终评价结果造成较大影响。

刘艳秋等[6]曾对多要素评价中权重系数的确定方法进行系统梳理。本研究应用多指标综合评价法对挖掘机动作协调性进行量化评分，通过分析各个方法的优劣，采用层次分析法确定权重；构造判断矩阵，将专家或操作手的经验转化成权重系数的思维过程数学化，避免过早地引入模糊信息，使得权重系数结果更加客观[7]；依据评价指标特点建立相应隶属函数，使指标评价值准确性提高；采用加法合成，将指标评价值与权重进行结合，最终得到挖掘机动作协调性的综合评分。

1 评价体系的建立

挖掘机动作协调性受多个因素影响，如动作响应是否及时，速度是否合适，运动是否平稳等。当需要对多个指标、多个单位同时进行评价时，通常采用多指标综合评价方法。这种评价方法的关键在于评价指标、权重系数和隶属函数的确定以及合成关系的处理。本研究将多指标综合评价法应用于挖掘机动作协调性评价之中，将协调性这一定性指标进行量化评分，以直观的形式体现挖掘机动作协调性优劣。评价步骤如下：

(1) 明确评价对象；

(2) 确定评价指标；

(3) 确定量化指标权重及评价值；

(4) 确定合成关系，求综合评价结果。

2 明确评价指标

2.1 评价指标选取原则

建立评价指标体系是对系统进行综合评价的基础。评价指标的选取是否合理直接影响到综合评价结果的科学性与准确性。确定系统的评价指标必须按照一定的原则进行分析与判断[8]：

(1) 系统性原则 动作协调性是多因素作用下的结果，对每个影响因素设立相应的评价标准，系统性地对动作整体进行评价；

(2) 可操作性原则 用于评价动作协调性的指标定义要清楚，便于采集数据和收集情况，避免带来不必要的麻烦；

(3) 突出性原则 指标的选择要全面，但每个指标对动作协调性的影响程度不同，应该区分主次；

(4) 定性与定量相结合原则 可以在定性分析的基础上进行量化处理。

2.2 评价指标

基于以上4个原则，确定挖掘机动作协调性评价指标：

(1) 动态响应性 先导手柄输入信号与执行机构输出之间的时间差值；

(2) 速度 出厂时机器定义每个动作规定行程与规定运动时间的比值；

(3) 冲击 执行机构启动阶段的压力超调量；

(4) 相对速度 当加入或退出某些执行机构动作时，剩余执行机构的速度变化量；

(5) 回转漂移 回转先导手柄信号停止后，挖掘机回转平台由于惯性等原因的溜车角度；

(6) 精控性 执行机构的速度(或角速度)和手柄输入信号之间的线性度，主要体现在手柄微操作中，当需要对执行机构速度进行小范围精细调整时，速度变化与手柄信号变化的跟随性；

(7) 吸空 运动过程中，液压缸大小腔压力突然接近0 MPa或者接近规定的吸空值，用接近吸空值的时间长短评价吸空。

3 确定评价指标权重及量化指标的评价值

3.1 确定评价指标权重

针对影响挖掘机动作协调性的多指标，采用层次分析法确定各指标的权重。权重的确定，原则上是根据专家或操作手经验，难点在于经验是一个模糊的概念，而权重是一组准确的数据，从人感知到数据量化的过程是难以实现的。借助层次分析法，专家或操作手只需提供各个指标的相对重要程度，采用如表1所示的九尺度判断法，在所有指标中，两两进行比较做出判断矩阵[9]，判断矩阵建立后，便可以从中求解出准确的权重系数，从而实现由人感知到量化数据的转化。

表1 重要程度表

针对影响挖掘机动作协调性的多指标，建立了表2所示的判断矩阵，判断矩阵收集影响挖掘机动作协调性指标的相对重要程度，用以求解各个指标的权重系数。判断矩阵中aij是表示第i行指标与第j列指标的相对重要程度，其中i=1，2，3，4，5，6，7；j=1，2，3，4，5，6，7。共统计了7个指标，构成七维判断矩阵，i=j时，对应判断矩阵中2个相同指标，同等重要记为1。

表2 判断矩阵

一致性检验：在对两两指标进行重要性比较时，由于评审专家的评价的主观性，会出现指标1>指标2、指标1<指标3、指标2>指标3的误判，针对这一问题，需要对判断矩阵的可行性即一致性进行检验[10]。

正互反矩阵中aij×aji=1，因此判断矩阵为正互反矩阵，如果正互反矩阵满足aij×ajk=aik，则为一致矩阵。在使用判断矩阵求解权重之前，必须要进行一致性检验，通过一致性检验的判断矩阵，求解出来的权重才具有实际意义。

理想的一致矩阵秩为1，并且只有1个最大特征值为n，其余都为0。判断矩阵越不一致时，最大特征值与n相差就越大。

一致性检验是通过计算一致性比例进行的。一致性比例CR与一致性指标CI、平均随机一致性指标RI间的关系为：

(1)

一致性指标计算公式为：

(2)

式中，λmax—— 判断矩阵最大特征值

n—— 判断矩阵维数

平均随机一致性指标RI只与判断矩阵的维数n有关，维数不同对应的平均随机一致性指标也不同，不需要计算，通过查阅得到，表3是部分维数对应的平均随机一致性指标。

表3 一致性指标RI

若求解得到的一致性比例CR<0.1，则可以认为判断矩阵的一致性可以接受[11]。一致性不可以接受，则需要改变判断矩阵中的元素，重新计算CR，直到可以接受为止[12]。

判断矩阵可以通过算术平均法、几何平均法以及特征值法计算出权重。此评价方法中采用特征值法进行求解，对最大特征值所对应的特征向量进行归一化处理，得到权向量。

3.2 确定量化指标的评价值

评价挖掘机动作协调性需要量化多个指标，但不同指标的计量单位不同，量化值不能直接合成[8]，需要进行无量纲化处理，即通过函数运算来消除量纲单位的影响，这就需要根据评价指标的特点建立相应的隶属函数。通过对隶属函数进行计算便可得到量化指标的评价值。

(1) 动态响应性：

(3)

式中，x1—— 实际测试的时间差值

a1—— 操作手反应时间加手柄死区行程时间

b1—— 挖掘机出厂设置的手柄输入与执行机构输出之间的最大响应时间

K—— 判别指标是否达到最低要求的逻辑值

(2) 稳态速度：

(4)

式中，x2—— 实测挖掘机执行机构速度

a2—— 可接受速度的最小值

b2—— 可接受速度的最大值

(3) 冲击：

(5)

式中，pmax—— 启动阶段最大超调下的压力

p—— 启动后稳态时的压力

(4) 相对速度：

(6)

式中， Δv—— 当加入或退出某执行机构动作时，对应其他动作在此阶段的速度变化量

v—— 未加入或退出之前其他动作的速度

(5) 精控性：

(7)

式中， Δvmax—— 理论曲线与实际曲线在相同的输入信号下输出的最大差值

v0—— 理论曲线与实际曲线在最小输入信号下的速度

vn—— 理论曲线与实际曲线在最大输入信号下的速度

(6) 吸空：

(8)

式中，x6—— 实测吸空时间

a6—— 允许的吸空值

(7) 回转制动：

(9)

式中，x7—— 实测漂移角度

a7—— 回转平台允许的漂移角度

4 确定合成关系及仿真验证

4.1 确定合成关系

在多指标综合评价体系中，单个指标的评价值与权重通过适当的方法合成可以得到系统的综合评价结果。通常采用的合成方法有加法合成、乘法合成和加乘混合等。不同的合成方法其数学表达式不同，具有的数学意义不同，因此所得到的综合评价结果也会存在差异，应根据评价系统的特点选择合适的合成方法。在评价挖掘机动作协调性中运用加法合成进行各指标评价值与权重的综合。

加法合成的公式如下：

(10)

(11)

式中，X—— 被评价事物得到的综合评价结果

Wi—— 各评价指标的权重

Yi—— 单个评价指标的评价值

N—— 评价指标个数

Ki—— 判别各评价指标是否达到最低要求的逻辑值，若达到最低要求Ki为1，否则为0

在加法合成中，各指标评价值间可以相互补偿，评价值较高的指标可以补偿评价值较低的指标，如果某个指标的评价值过低，却被其他指标补偿，导致最终的综合评价值依然较高，这种情况显然是不合理的。采用有约束的线性加权办法能很好的解决加法合成这一缺点，当某个指标的评价值过低时，将逻辑系数K取0，则最终的综合评价结果为0，使之不具有评价意义[13]。

4.2 多指标综合评价方案应用

以某公司挖掘机为例，使用多指标综合评价法对斗杆挖掘加铲斗挖掘复合动作协调性进行评价。应用MATLAB-Simulink搭建多指标综合评价程序，将试验采集数据输入程序中后，即可得到挖掘机复合动作协调性的综合评价结果，评价程序如图1所示。

图1 复合动作MATLAB-Simulink评价程序

1) 确定权重系数

判断矩阵、权重分配表、各指标评价值如表4～表6所示。从权重分配表可以看出，复合动作协调性中相对速度所占的权重较大。

表4 判断矩阵

表5 权重分配表

2) 确定评价指标及其评价值

读取先导压力开始上升时间与液压缸开始动作时间的差值Δt，斗杆Δt1为0.26 s，铲斗Δt2为0.07 s，斗杆的动态响应有待提高。将时间差Δt代入动态响应隶属函数中并与动态响应性所占权重相乘，即可得到复合动作中动态响应单项指标评价值为66。

执行机构行程与时间比值，得到稳态平均速度，其中斗杆挖掘的稳态平均速度为468 mm/s，铲斗挖掘的稳态平均速度为342 mm/s，将稳态平均速度v代入到速度隶属函数中并与速度所占权重相乘，即可得到复合动作中速度单项指标评价值为72.5。

读取挖掘过程中液压缸大腔压力的最大超调值Δσ，斗杆Δσ为12.9 MPa，铲斗Δσ为16.5 MPa，从曲线及超调值可以看出，挖掘机的压力冲击较大。将超调值Δσ代入冲击的隶属函数中并与冲击所占权重相乘，即可得到复合动作中冲击单项指标评价值为63。

从斗杆和铲斗液压缸大腔压力数据中可以看出，液压缸大腔压力突然接近0 MPa或者接近规定的吸空值的时间极短，完全小于吸空允许的阈值，即斗杆挖掘和铲斗挖掘中不存在吸空现象， 吸空这项指标的评价值均为100，因此复合动作吸空评价值为100。

在斗杆挖掘作业时加入铲斗动作，由于流量变化会导致斗杆运动速度突变，读取斗杆运动速度变化量Δv为494 mm/s。在斗杆挖掘加铲斗挖掘复合动作时，斗杆动作退出后，铲斗的运动速度也会产生变化，读取铲斗速度变化量Δv为95 mm/s，从曲线及速度变化值可以看出，挖掘机在执行机构增减过程中的相对速度变化较大。将其带入到相对运动速度的隶属函数中并与相对速度指标所占权重相乘，即可得到复合动作中相对速度变化单项指标评价值为54。

采用最小二乘法拟合先导压力-速度关系，得到实际曲线，根据其输入信号理论计算其线性度函数关系，得到其理论曲线，读取理论曲线与实际曲线在相同的输入信号下输出的最大差值Δvmax：斗杆Δvmax为206 mm/s，铲斗Δvmax为148 mm/s；铲斗理论曲线与实际曲线在最小输入信号下速度v0：斗杆Δv0为459 mm/s，铲斗Δv0为4 mm/s；理论曲线与实际曲线在最大输入信号下的速度vn：斗杆vn为871 mm/s，铲斗vn为398 mm/s，将其代入精控性隶属函数中并与精控性指标所占权重相乘，即可得到复合动作中精控性单项指标评价值为56。从精控性曲线中可进一步的看出，手柄输入信号与执行机构输出信号之间的线性度较差。

综上，将试验获得的数据经处理后代入相应的隶属函数中，可得各个指标的评价值，汇总如表6所示。

从图2～图11中可以看出，某型号挖掘机在斗杆挖掘加铲斗挖掘复合动作中，压力冲击、相对速度的变化均较大，精控性较差，与表6中冲击、相对速度、精控性的的评分基本保持一致。因此，需要减小挖掘机压力冲击、相对速度变化，提高其精控性。最后，采用加法合成法进行综合计算，得到斗杆挖掘加铲斗挖掘复合动作的综合评价值为66.1。

图2 斗杆挖掘动态响应性

图3 铲斗挖掘动态响应性

图4 斗杆挖掘速度

图5 铲斗挖掘速度

图6 斗杆挖掘冲击

图7 铲斗挖掘冲击

图8 铲斗进入相对速度

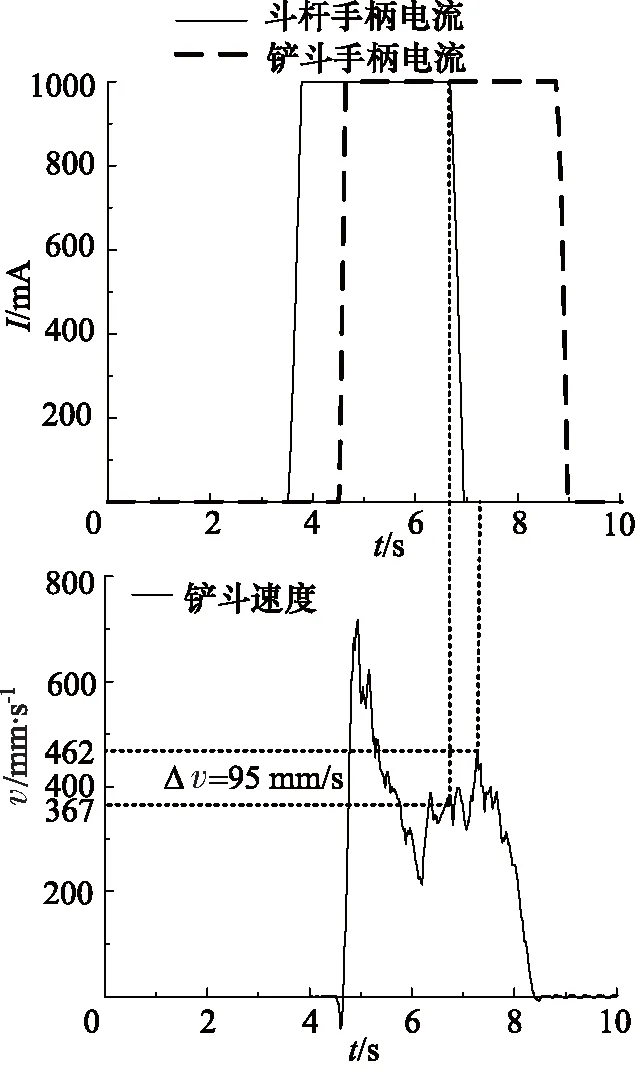
图9 斗杆退出相对速度

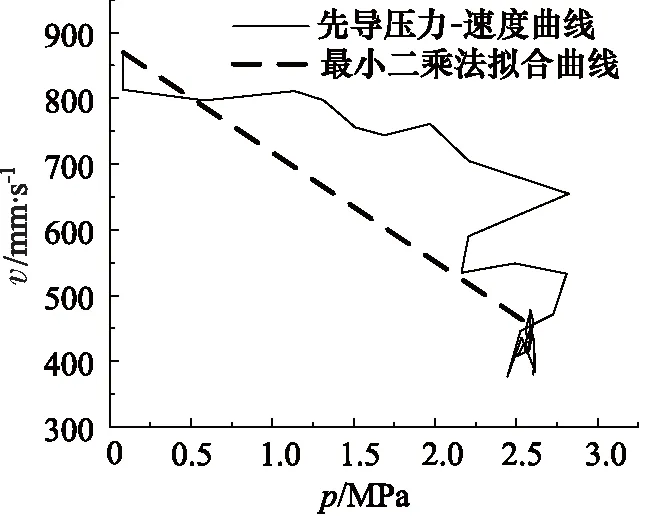
图10 斗杆挖掘精控性

图11 铲斗挖掘精控性

表6 各指标评价值

5 结论

针对挖掘机动作协调性难以客观评价的问题，在较少定量信息支持的前提下，以影响挖掘机动作协调性的多指标为出发点，通过层次分析法，达到了将操作手经验的模糊信息转化为精确权重系数的目的，从而得到了一组既符合实际又有理论依据的权重，并对各个指标分别应用合适的隶属函数计算其评价值，完成了评价中多指标、多准则的复杂评价任务，以加权求和的方法计算评价值，考虑加法合成存在各指标间的线性补偿，引入逻辑系数K对评价结果进行修正，克服了其他指标对某个或某些极低评价值的补偿导致评价结果不准确的问题。基于某型号挖掘机的实验数据，进行了MATLAB-Simulink仿真验证，得到较为客观的综合评价结果，该评价方法可以定量评价挖掘机动作协调性，对研发人员基于该评价结果做出分析决策具有实际指导意义。