页岩断层滑移量计算模型及影响因素研究*

刘鹏林 李 军, 席 岩 连 威 张小军 郭雪利

(1.中国石油大学(北京)石油工程学院 2.中国石油大学(北京)克拉玛依校区石油学院 3.北京工业大学建筑工程学院 4.中国石油集团工程技术研究院有限公司)

0 引 言

在页岩气水平井多级压裂过程中，套管变形问题显著，严重影响了页岩气产能建设，增加了开采成本[1-3]。根据页岩气井多臂井径测井数据[4-7]，可准确判断出井下套管变形形态。井下套管变形主要分为5类：挤压变形、屈曲变形、弯曲变形、剪切变形和孔洞[8]。其中，以套管剪切变形占比最大，达到全部变形的49%。

国内外学者针对断层滑移发生机理及断层滑移与套管剪切变形形态之间的关系进行了相关研究。XI Y.等[4]分析了页岩气水平井多级压裂过程中水泥环对套管变形的影响规律；王素玲等[9]进行了页岩层剪切滑移对套管塑性应变的模拟；席岩等[5]研究了体积压裂过程中页岩储层各向异性及岩性界面等因素对套管应力的影响规律；陈朝伟等[6]结合摩尔-库伦准则，给出了断层滑移发生条件；王倩琳等[10]认为页岩气多级压裂过程中压裂液注入到地层中易激活断层发生滑移；沈新普等[11]发现套管变形与微地震信号间存在联系，建立了有限元模型分析压裂压力与套管变形之间的关系；王光磊等[12]提出了新的井筒载荷计算方法与现场保障井筒完整性措施。陈升等[13]针对体积压裂过程中的套管力学行为进行了研究；陈朝伟等[14]和GUO X.L.等[15]基于震源机制关系，分别建立了断层滑移评价机制，反演了断层滑移距离；席岩等[16]根据断层滑移距离分析了套管内径的变化规律。

以上研究只给出了套管剪切变形量与断层滑移之间的关系，不能有效反映页岩地层大尺度条件下的断层滑移规律，未能给出断层滑移量的有效计算方法，难以对后续压裂施工进行指导。鉴于此，本文基于页岩断层受力形态，通过ABAQUS建立了一种考虑断层上、下部地层影响的页岩断层滑移模型，研究了断层滑移量随地层参数的变化规律。研究结果可为页岩气多级压裂过程中压裂参数控制提供参考。

1 断层滑移量计算方法

1.1 断层滑移物理模型

有关断层滑移的解析模型与数值模型中，通过定义断层滑移量来量化研究套管剪切变形形态与断层滑移之间的关系，较少考虑断层滑移过程中断层受力以及断层上、下部地层对滑移过程的影响。鉴于此，本文建立了页岩断层滑移物理模型，如图1所示。模型共分为3部分：上部地层、断层(断层1与断层2)和下部地层。断层滑移过程如下：压裂作业导致压裂液进入断层内致使断层1与断层2间接触面摩擦因数降低，原有地层系统的受力平衡被破坏，断层开始发生滑移；滑移发生后，下部地层对断层产生新的支撑力，促使断层系统达到新的平衡状态后，断层滑移过程结束。由于受力发生改变，断层1与断层2产生位移，通过计算断层面摩擦因数改变后的断层1与断层2位移差得到断层滑移量。

图1 断层滑移物理模型Fig.1 Physical model of fault slip

1.2 断层滑移量计算方法

根据1.1中模型，做出如下基本假设：

(1)假设断层与其上、下部地层均为均质地层；

(2)忽略页岩气水平井眼穿越断层对断层受力的影响；

(3)忽略压裂过程中地层孔隙压力变化的影响，仅考虑断层面处摩擦因数变化。

在上述条件下，对断层进行受力及位移分析，以计算断层滑移量。对断层1进行分析，在断层滑移过程中断层1受力为：

G1+σv-σncosθ-μσnsinθ=F1

(1)

式中：G1为断层1所受重力作用于下部地层的体力，MPa；σv为垂向地应力，MPa；σn为水平最小地应力，MPa；θ为断层倾角，(°)；μ为断层面摩擦因数，无量纲；F1为断层1所受下部地层支撑力，MPa。

其中，断层下部地层对断层1的支撑力F1为：

F1=E2ΔX1/S1

(2)

式中：E2为下部地层岩石弹性模量，MPa；ΔX1为断层1的位移量，m；S1为断层1的长度，m。

因此，断层1受到地应力、重力、摩擦力和下部地层支撑力，当摩擦因数发生变化后，受力及位移同时发生改变并重新达到受力平衡。而在断层滑移及地应力共同作用下，断层1在摩擦因数变化后产生位移量为ΔX1。

其次，对断层2进行分析。同理，断层2在断层滑移过程中受力为：

G2+σv-σncosθ+μσnsinθ=F2

(3)

式中：G2为断层2所受重力作用于下部地层的体力，MPa；F2为断层2所受下部地层的支撑力，MPa。

其中断层下部地层对断层2的支撑力F2为：

F2=E2ΔX2/S2

(4)

式中：ΔX2为断层2的位移量，m；S2为断层2的长度，m。

因此，断层2受到地应力、重力、摩擦力和下部地层支撑力并达到受力平衡，在断层滑移及地应力共同作用下，断层2在摩擦因数变化后所产生的位移量为ΔX2。

最后，对断层1和断层2组成的系统进行受力分析，方程如下：

G1+G2+σv=F1+F2

(5)

联立式(1)～式(5)，求解可得ΔX1与ΔX2，二者位移差ΔX即为断层滑移量：

ΔX=ΔX1-ΔX2

(6)

2 数值模型

2.1 网格模型

将断层滑移物理模型导入ABAQUS有限元分析软件中，建立如图2所示的页岩气断层滑移网格模型。假设地层弹塑性力学性质不变，为消除边界对断层的影响，将模型尺寸定为300 m×300 m×300 m，上、下部地层高度为100 m，断层高度为100 m，断层倾角为45°。网格采用结构化六面体网格，并进行网格无关性计算，选取了无量纲长度5作为网格长度。

图2 页岩气断层滑移网格模型Fig.2 Mesh model of shale gas fault slip

2.2 材料参数及边界条件

2.2.1 材料参数设置

数值模拟过程中，取四川某区块页岩气水平井所处位置地层参数，具体计算参数如下：

断层岩石弹性模量为20～40 GPa，泊松比为0.16～0.20；上部地层及下部地层岩石弹性模量为20～40 GPa，泊松比为0.16～0.20；断层1与断层2接触面摩擦因数为0.6～0.9；地层岩石密度均设定为2 700 kg/m3；重力加速度为9.81 m/s2。

2.2.2 边界条件及载荷设置

断层1与断层2之间接触面设定为surface-to-surface接触模式。其中，法向接触行为设定为“hard”模式，切向接触行为设定为摩擦接触，摩擦因数设定为0.6。断层与上、下部地层接触面采用“绑定”模式。

断层下部地层底边采用固定位移约束，四周各面采用法向位移为0的方式进行约束。地层地应力采用Predefined-field模块进行施加，根据井史资料，设定模型最小水平地应力60.0 MPa，最大水平地应力65.0 MPa，垂向地应力68.5 MPa。

3 结果分析

3.1 滑移规律

分别选取断层顶部、中部和底部位置观测横向上位移情况，结果如图3所示。由图3可知：由于摩擦因数降低，在断层1与断层2接触面处发生了位移差，该位移差即为断层滑移量；从断层顶部至断层底部，断层滑移量逐渐降低。

图3 不同位置处断层滑移量的变化规律Fig.3 Change rule of fault slip at different positions

图4为沿断层面方向由顶部至底部断层滑移量的变化规律。沿断层面方向上的不同位置，断层顶部为0 m、断层面底部为144 m。由图4可知：沿断层面方向断层滑移量整体呈下降趋势，呈倒S形；在断层顶部和底部区域，断层滑移量下降较快，中部区域下降较平缓，这是由于断层及下部地层岩石产生弹塑性变形。

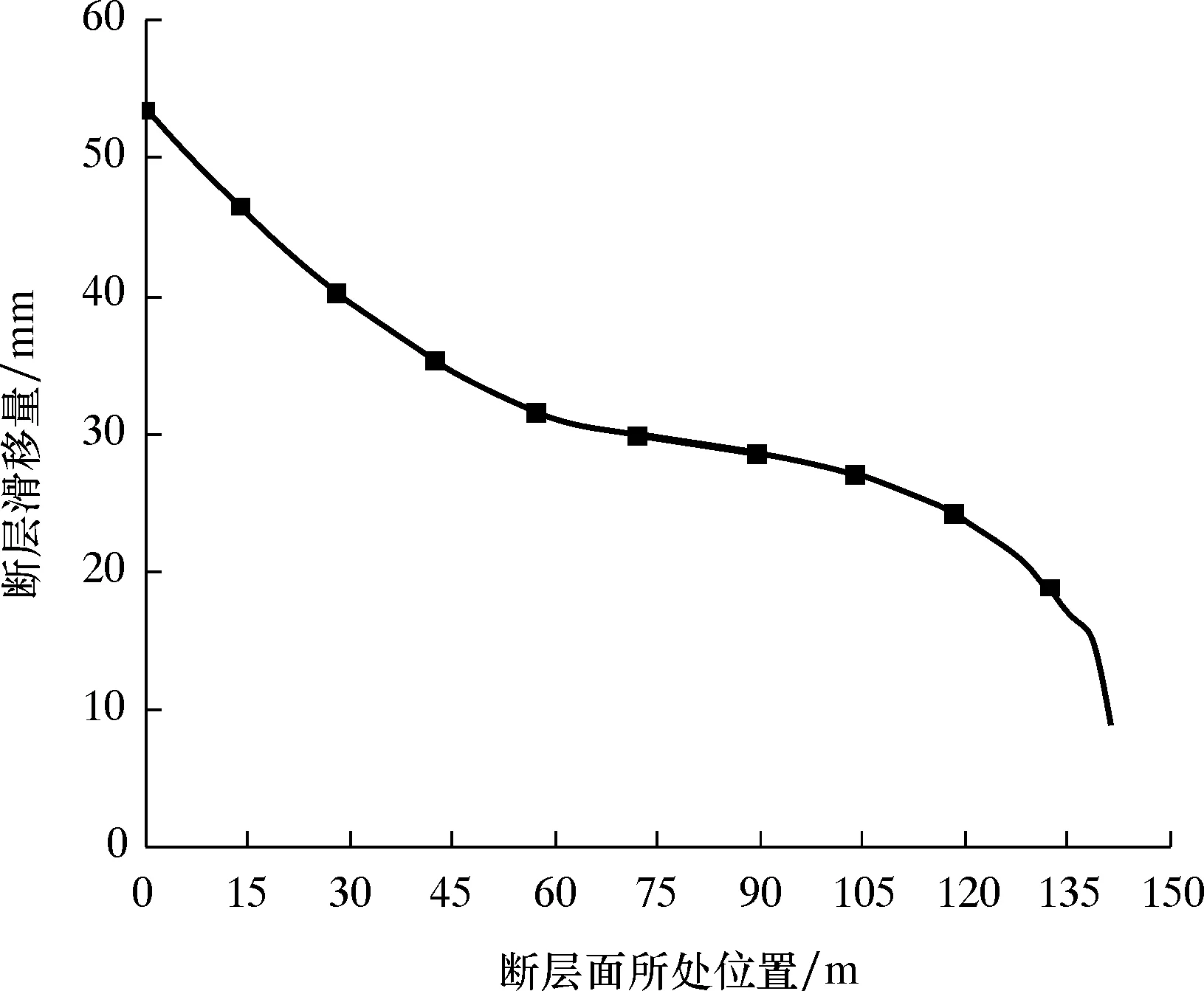
图4 断层滑移量沿断层面的变化规律Fig.4 Change rule of fault slip along fault plane

所以，在施工中应注意水平井井眼轨迹与断层相对位置。若井眼轨迹处于断层顶部和中部时，则会产生较大的断层滑移量，此时靠近断层附近施工应减小压裂排量和压力或不压裂，避免激活断层；若井眼处于断层底部位置，断层滑移量相对较小，对井筒剪切变形影响较小，此时可适当增加压裂液排量与压力，保证储层改造充分。

3.2 敏感性参数分析

3.2.1 断层面摩擦因数

在断层附近进行压裂作业时，压裂液易进入断层面内，进入断层面内的液体越多，断层面摩擦因数越小。分别将断层接触面摩擦因数设定为0.6、0.7、0.8和0.9，计算不同断层面摩擦因数下断层滑移量沿断层面的变化规律，结果如图5所示。

图5表明，随着摩擦因数减小，断层滑移量逐渐增大，断层面摩擦因数增大至0.9时，断层最大滑移量为41 mm；断层面摩擦因数降低至0.6时，断层最大滑移量增大至54 mm；断层最大滑移量相差达13 mm。依据文献[17]，断层滑移量每降低10 mm，套管变形量可降低8 mm，可有效改善套管变形形态。因此，在断层附近施工时，应降低压裂注液量及压裂排量，减小压裂液进入断层面内的体积，从而减缓断层面摩擦因数的下降，达到降低断层滑移量，改善套管剪切变形的目的。

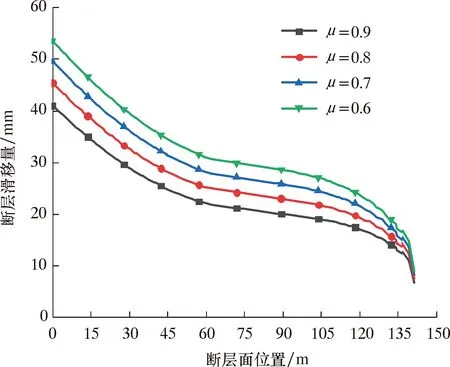
图5 断层面摩擦因数对断层滑移量的影响Fig.5 Influence of friction coefficient of fault plane on fault slip

3.2.2 断层岩石力学参数

断层岩石力学参数随储层性质不同而变化。图6为断层岩石不同弹性模量与断层滑移量之间的关系。保持其他条件不变，分别设定断层岩石弹性模量为20、30和40 GPa。图7为断层岩石不同泊松比与断层滑移量之间的关系。分别设定断层岩石泊松比ν为0.16、0.18和0.20。

图6 断层岩石弹性模量对断层滑移量的影响Fig.6 Influence of elastic modulus of fault rock on fault slip

由图6可知：断层岩石弹性模量越大，断层滑移量越小；断层岩石弹性模量增加10 GPa，断层滑移量在断层顶部可降低5 mm左右。所以，弹性模量较大的页岩地层可采用更大的压裂压力和排量；弹性模量较小的页岩地层在断层附近作业时应降低压裂压力和排量，避免产生较大的断层滑移量。

由图7可知：断层岩石泊松比越大，断层滑移量越小；不同泊松比条件下断层滑移量相差较小，在断层顶部滑移量差距最大区域，仅相差1 mm。因此，断层岩石泊松比不是影响断层滑移的主要因素。

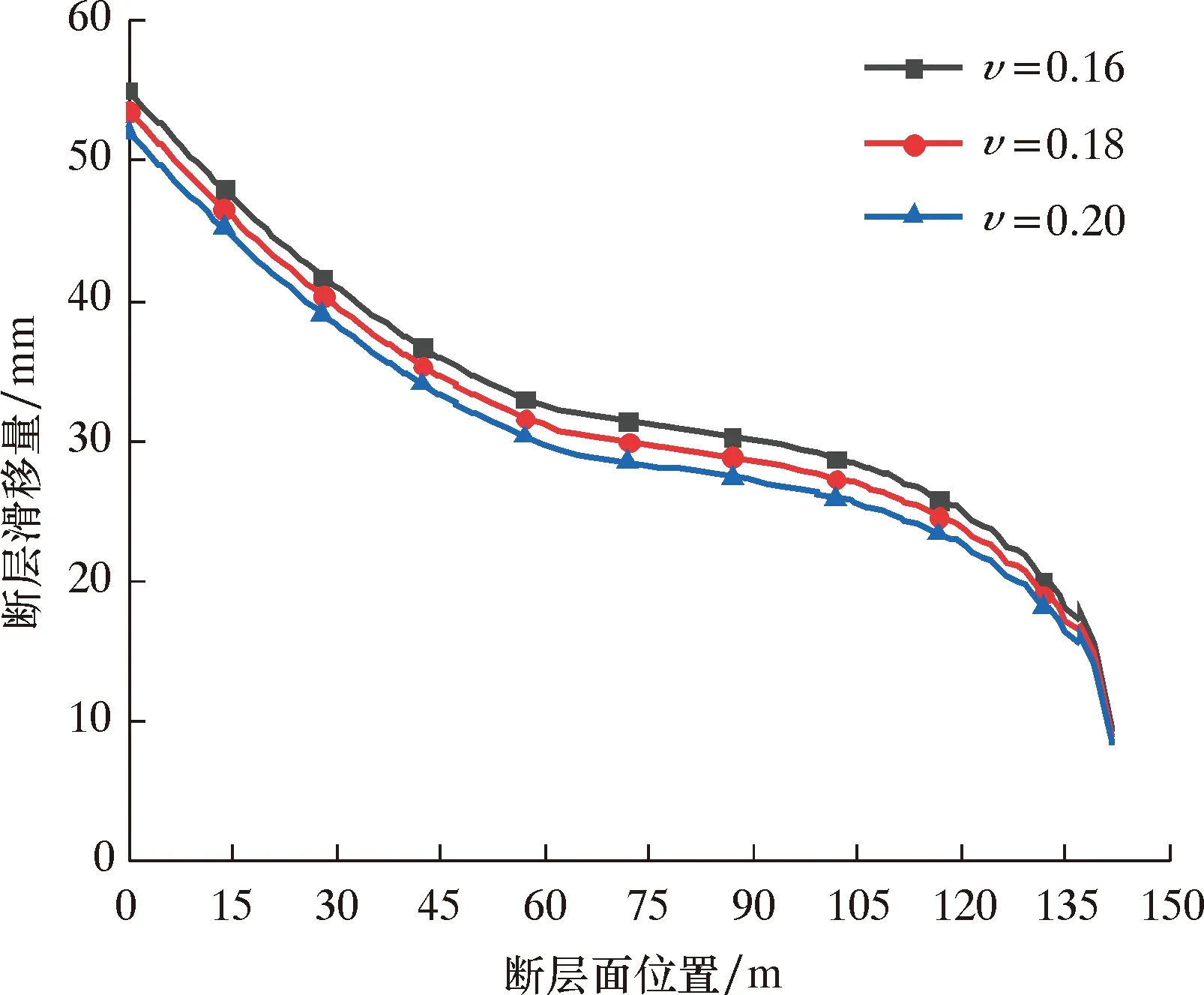
图7 断层岩石泊松比对断层滑移量的影响Fig.7 Influence of Poisson’s ratio of fault rock on fault slip

3.2.3 下部地层岩石力学参数

下部地层岩石由于岩性不同其力学参数会发生变化。设定下部地层岩石弹性模量分别为20、30和40 GPa，泊松比分别为0.16、0.18和0.20进行分析。图8及图9分别为不同下部地层岩石弹性模量和泊松比条件下断层滑移量沿断层面的变化规律。

图8 下部地层岩石弹性模量对断层滑移量的影响Fig.8 Influence of elastic modulus of rock in the lower strata of the fault on fault slip

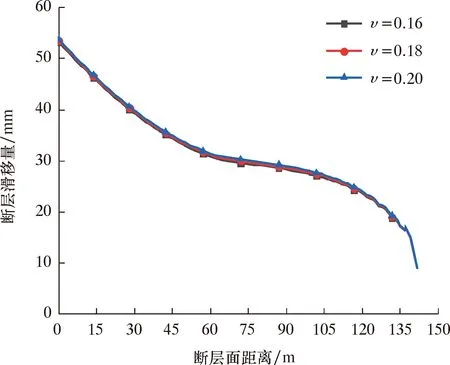
图9 下部地层岩石泊松比对断层滑移量的影响Fig.9 Influence of Poisson’s ratio of rock in the lower strata of the fault on fault slip

由图8可知：下部地层岩石弹性模量越小，断层滑移量越小；下部地层岩石弹性模量为40 GPa时，断层顶部滑移量在58 mm左右；弹性模量为20 GPa时，断层顶部滑移量为50 mm，降低8 mm左右；在断层中部断层滑移量相差最大，达20 mm左右。因此，断层下部地层越“硬”，断层滑移量越大，断层下部地层越“软”，则断层滑移量越小。

由图9可知，随着下部地层岩石泊松比的增加，断层滑移量无明显变化。因此下部地层岩石泊松比不是影响断层滑移量的主要因素。

同时，对比3.2.2节中结果，断层岩石泊松比及下部地层岩石泊松比均对断层滑移量无明显影响。断层下部地层岩石弹性模量的变化比断层岩石弹性模量变化对断层滑移量的影响更加明显，下部地层越“硬”，所产生的断层滑移量越大，套管变形量越大。

3.2.4 地应力

不同区块及不同深度条件下的页岩储层地应力均不同。在模型中分别设定垂向地应力为60、70和80 MPa，最小水平地应力为60、65和70 MPa，对比分析不同地应力条件对断层滑移量的影响，结果如图10和图11所示。

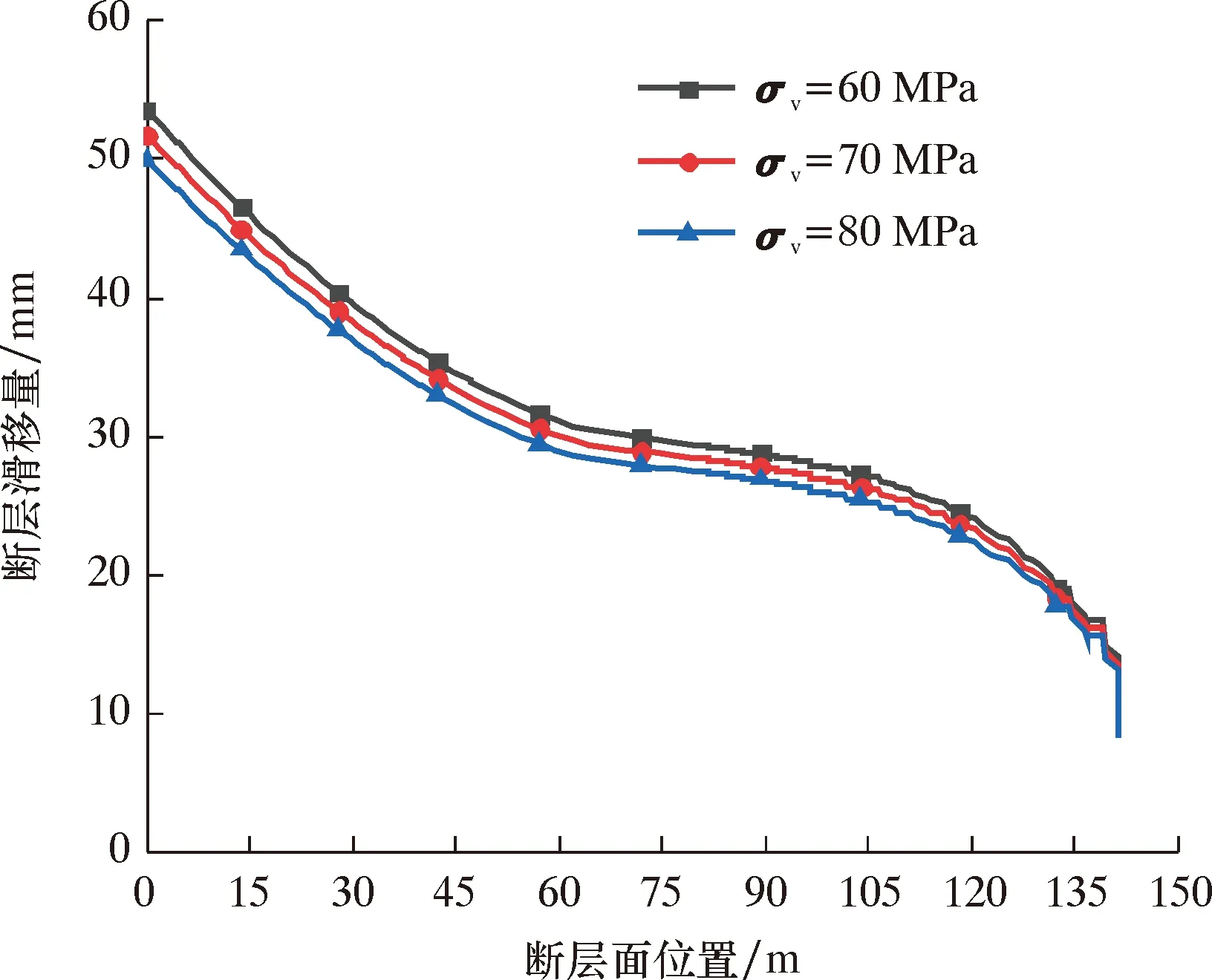
图10 垂向地应力对断层滑移量的影响Fig.10 Influence of vertical in-situ stress on fault slip

由图10可知：随着垂向地应力的增大，断层滑移量逐渐增大；在断层顶部，垂向地应力每增大10 MPa，断层滑移量增加约2 mm，断层滑移量变化较小。由图11可知：随着最小水平地应力的增加，断层滑移量也逐渐增加；水平最小地应力每增加10 MPa，断层滑移量增加10 mm。因此水平最小地应力对断层滑移的影响更大。水平最小地应力较大的地层，可能引发更大的断层滑移量，套管剪切变形问题更严重。

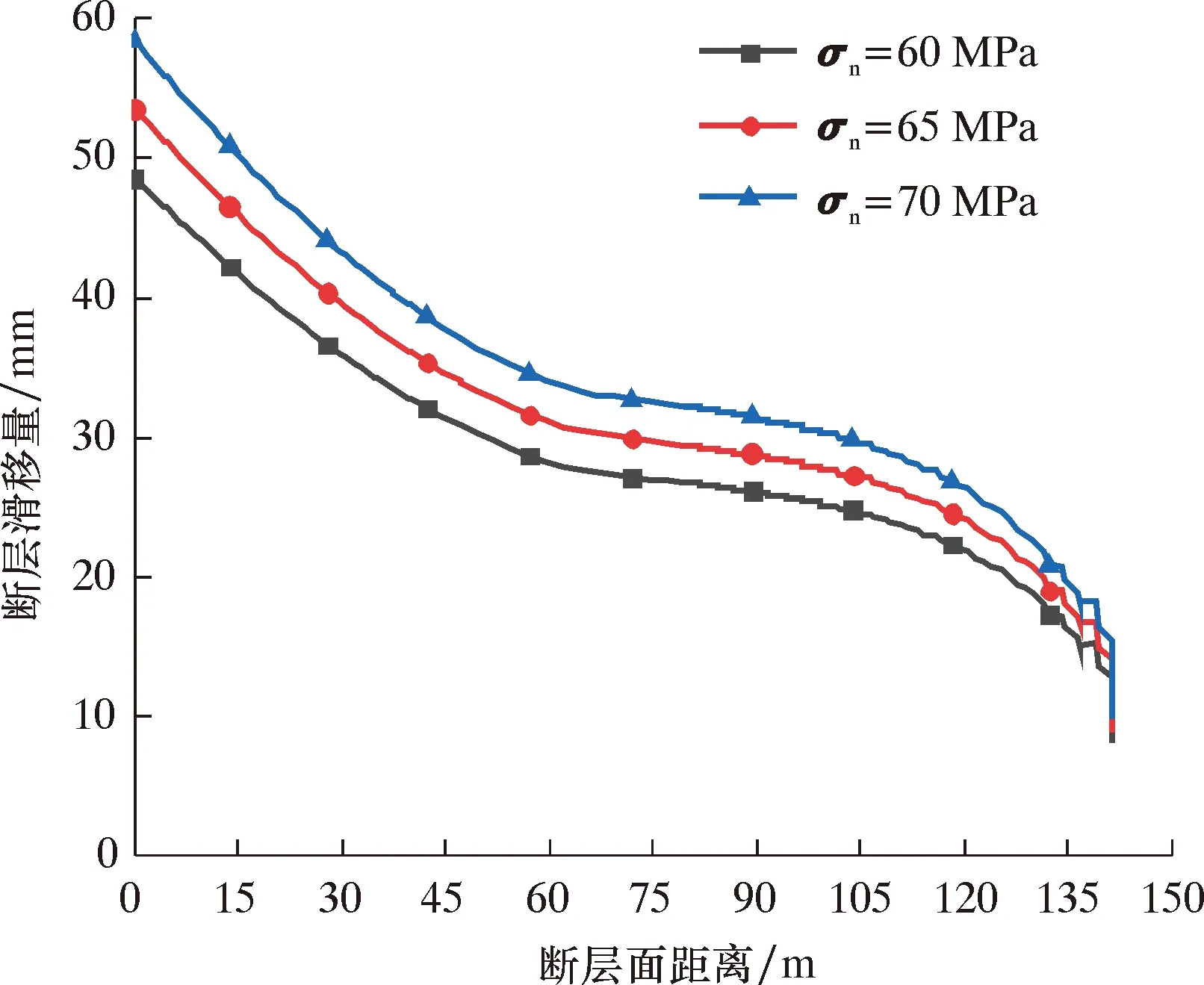
图11 水平最小地应力对断层滑移量的影响Fig.11 Influence of horizontal minimum in-situ stress on fault slip

4 结 论

(1)建立了一种考虑断层上、下部地层对断层滑移影响的页岩断层滑移新模型，并可通过有限元软件计算得到断层滑移量的变化规律。

(2)数值试验结果表明，断层滑移量由断层顶部至断层底部逐渐减小，总体趋势呈倒S形，在断层顶部和底部下降较快，断层中部断层滑移量基本保持不变。

(3)断层面摩擦因数减小、断层岩石弹性模量降低、下部地层岩石弹性模量增大和最小水平地应力增加均会增加断层滑移量；断层岩石泊松比、下部地层岩石泊松比和地层垂向地应力不是断层滑移量变化的主要影响因素。