基于非线性能量阱的桥梁振动能量采集装置的适用性研究
2022-10-17杨兴森李照宇王绍华豆银玲占玉林赵人达
杨兴森, 李照宇, 王绍华, 豆银玲,3, 占玉林, 赵人达
(1.西南交通大学 土木工程学院,成都 610031; 2.奥克兰大学 机械工程系,新西兰 奥克兰 1010; 3.西南交通大学 高速铁路线路工程教育部重点实验室,成都 610031)
近年来,随着我国交通基础项目建设的大力推进,铁路桥梁工程也出现了迅猛的发展,截至2017年底,我国高速铁路里程已达到2.5万km,其中桥梁占线路总长度的50%[1]。桥梁作为轨下重要的基础结构,对列车运营平稳性和安全性具有重要影响。在此大背景下,为了对桥梁的性能以及可靠性进行实时监测,建立起一套智能可靠的桥梁健康监测管理系统尤为重要。而传统桥梁健康监测传感器的供电方式主要是可替换式的电池,而电池更换造成了人力物力的增加,不太符合可持续“新基建”的发展理念。为了实现再生能源低成本规模化的开发利用,基于能量采集的自供电体系近年来受到了学者们的广泛关注与研究[2-3]。而振动能作为桥梁环境周围最为常见且极易获取的能量,目前成为桥梁自供能传感器能量采集来源的首选[4-5]。
针对桥梁振动能量采集方法,已有学者进行了研究。Karimi等[6]从理论和试验方面研究了悬臂梁式压电能量采集装置在桥梁振动中的能量采集效果,并得到其共振频率下的最佳阻性负载。另外,Zhang等[7]基于实际车桥耦合试验平台,从理论与试验分析发现,压电能量采集装置在桥梁跨中位置可以达到较高的能量采集效率,且当能量采集装置的固有频率等于车桥耦合振动频率时,其电压输出较高。以上振动能量采集方法都是基于线性共振的基本原理,采集装置通常只在其谐振频率附近的有限带宽内采集振动能量。而实际的桥梁振动属于宽频振动。因此,研究与设计能量采集装置在更宽频带采集能量更具有实际意义,也是学者们近年来的研究热点之一。
引入非线性技术作为一种已被证明能够有效提高能量采集装置工作带宽和效率的方式,近年来在能量采集领域得到了广泛的研究[8]。其中,非线性能量阱(nonlinear energy sink, NES)以其结构简单、工作频带宽且鲁棒性高等优势,受到了能量采集研究学者们的关注[9-12]。NES主要由较轻的质量单元、强非线性刚度和阻尼元件组成[13]。研究表明,当主体结构传递过来的能量达到某一特定阈值时,振动能量将不可逆的转移到NES中,并通过NES的阻尼在局部耗散,即靶向能量传递(targeted energy transfer, TET)[14]。通过将NES传递过来的主体振动能量加以转换和采集,即可实现无需调谐的宽频、高效能量采集。Kremer等基于电磁转换方式设计出一款能量采集装置,试验表明,在冲击荷载和简谐荷载激励作用下,该装置在较宽频域内表现出良好的能量采集性能。Xiong等设计与研究了基于压电转换方式的NES能量采集装置在谐波激励作用下的动力特性和能量采集能力,通过理论分析和仿真模拟,结果表明NES的引入明显提高了能量采集效率。Li等在此基础上,研究了该装置在连接同步电荷提取电路(synchronized charge extraction circuit, SCEC)后的动力特性能量采集性能,该研究首先通过等效阻抗法对接口电路进行简化,然后使用谐波平衡法分析得到了在简谐激励下该系统的动力特性近似解析解,最终进行电路仿真和试验复核,结果表明该系统能够在较宽的频率范围内采集能量,且能量采集效率与该系统接口电路中的负载电阻大小无关。
据笔者所知,目前NES技术在桥梁结构振动能量采集方面的研究和应用还不多见。基于此,本文以铁路简支梁桥为例,开展了基于NES的桥梁振动能量采集装置适用性研究。首先测试与表征了NES装置的非线性力学特性,然后运用车辆-轨道-桥梁垂向耦合动力学理论,计算得到了该桥梁跨中的振动响应范围。并在此基础上,运用有限元法建立NES-桥梁装置的动力学方程,探究不同激励条件下NES装置的力学特性及其能量采集效果。本研究旨在为基于桥梁结构振动的非线性能量采集装置的设计与研究提供理论依据。
1 NES装置原理及参数测量
NES作为一种具有极强非线性刚度的结构,能够高效地采集主体结构的振动能量。简化的NES能量采集系统物理模型如图1所示。系统由振动主结构与压电NES结构组成,振动主结构由质量Mp、线性刚度Kp和阻尼Cp组成,压电NES结构由质量Ma、非线性刚度Ka和阻尼Ca组成。在主结构振动激励作用下,压电换能器产生正压电效应,将振动能量转化为电能。因此,能量采集系统的系统方程可以表示为
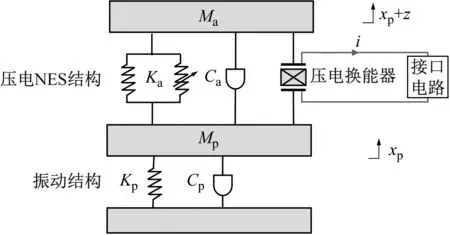
图1 NES能量采集系统Fig.1 Representation of the NES energy harvesting system
(1)
(2)
式中:xp为振动主结构的位移;z为NES结构相对于振动主结构的位移;Θ为机电耦合系数;V为电路电压输出值;F(k,z)为弹簧刚度提供的非线性回复力。
由于NES的力学特性受自身物理参数的影响较大,需要研究NES的非线性力学特性并测定NES装置的关键参数用于进一步的数值仿真分析。
制作NES能量采集装置,如图2所示。该装置由一个双晶片压电悬臂梁和一个安装有三块圆柱体磁铁的悬臂端质量块组成。在亚克力板外框架上安装另外三块可调节距离的圆柱体磁铁,它们与压电悬臂梁端质量块上的磁铁一一互斥。其中,两侧的磁铁在悬臂梁振动时,给质量块施加附加排斥力,顶部的磁铁在质量块偏离中心平衡位置时,对质量块施加一定的偏心力,通过调节外框架上的磁铁与NES质量块的距离来改变磁铁间排斥力大小,进而使得NES装置具有极强的非线性刚度。在实际桥梁结构应用中,将NES装置的底座与桥梁侧端相连,使得在桥梁受迫振动激励下,悬臂梁以其弱轴方向上下振动,促使悬臂梁上下表面的压电片材料产生正压电效应,并通过与接口电路连接输出电能。

图2 NES试验装置Fig.2 NES experiment setup
其中,NES质量包括悬臂梁自由端的质量块和磁铁块的质量。在短路条件下,对NES悬臂梁端质量块施加一个较小的初始位移,以保证其自由衰减响应是准线性的,记录下质量块的位移以及惯性力变化数据。首先,阻尼系数根据文献[15]所述,利用位移衰减曲线,通过对数衰减法得到其阻尼系数Ca。
根据式(2),得到NES中质量块的运动方程为
(3)
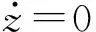
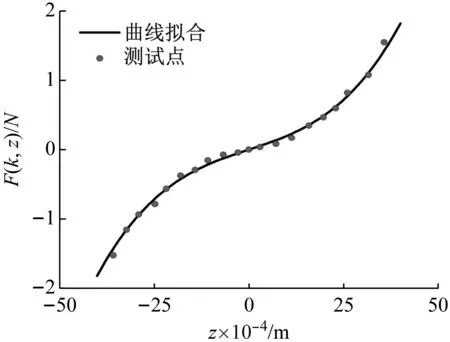
图3 NES回复力-位移关系Fig.3 Relationship between NES restoring force and displacement
进而通过曲线拟合得到NES回复力-位移曲线。曲线拟合结果与文献[16]所述类似,NES回复力与位移关系满足式(4),进而得到该NES装置弱线性刚度值K1和强非线性刚度值K3。
F(k,z)=K1z+K3z3
(4)
综上,通过测试NES装置得到其关键参数如表1所示。

表1 NES装置参数Tab.1 Parameters of NES
2 模型建立
2.1 车辆-轨道-桥梁垂向耦合动力学模型建立
2.1.1 车辆系统模型
随着数字化信息的不断建设,对广播电视进行无线数字化覆盖建设,能够在不同层次满足人们的需求。为了提升全国广播电视服务的水平和质量,全面建设广播电视中的无线数字化覆盖工程成为了国家当前需要实现的主要任务之一,对广播电视的传播力和影响力进行有效的加强,对社会主义核心价值观有一定的推进作用,快速实现无线广播电视的数字化建设。随着科学技术在各行各业的中的具体深入,广播电视也随着潮流的发展在不断地改善,使得广播电视的发展方向更加丰富,对传统媒体与新媒体之间的有效联系也有一定的积极作用,使信息更加准确。
车辆被模拟为由车体、转向架和轮对组成的多刚体系统,如图4所示。该系统考虑了车体的沉浮(Zc)和点头(βc)运动、前后转向架的沉浮(Zt1,Zt2)和点头运动(βt1,βt2),以及四个轮对的垂向运动(Zwi,i=1~4),共计10个自由度。车辆模型关键参数如表2所示。
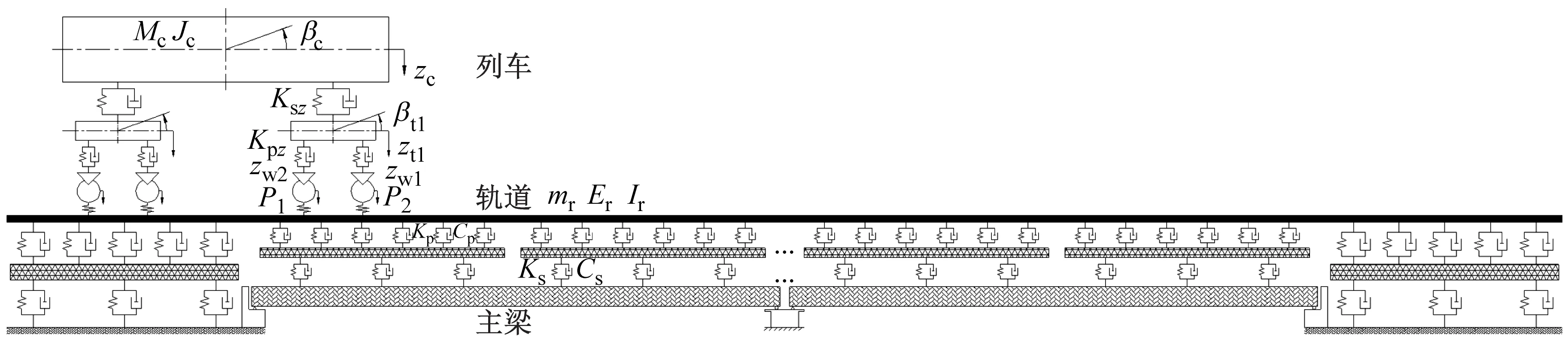
图4 车辆-轨道-桥梁系统振动模型Fig.4 Vibration model of vehicle-track-bridge system
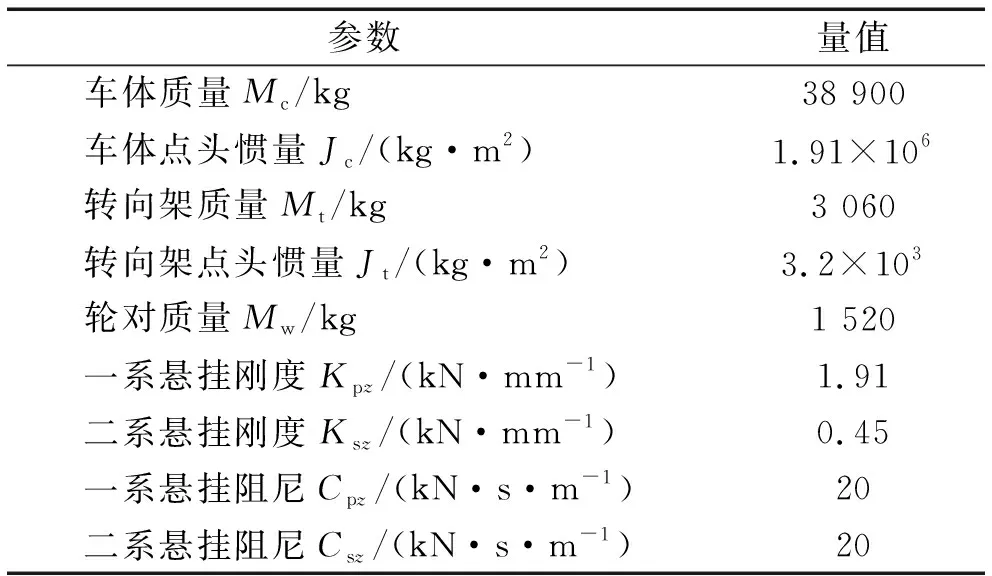
表2 车辆模型参数Tab.2 Parameters of vehicle model
2.1.2 轨道系统模型
从图4可知,轨道采用钢弹簧板式无砟轨道,并模拟为双层叠合梁模型。在该振动模型中,钢轨被视为离散弹性点支承基础上的Euler梁,轨道板则按支承在线性弹簧和线性阻尼上的有限长自由梁考虑。轨道模型关键参数如表3所示。
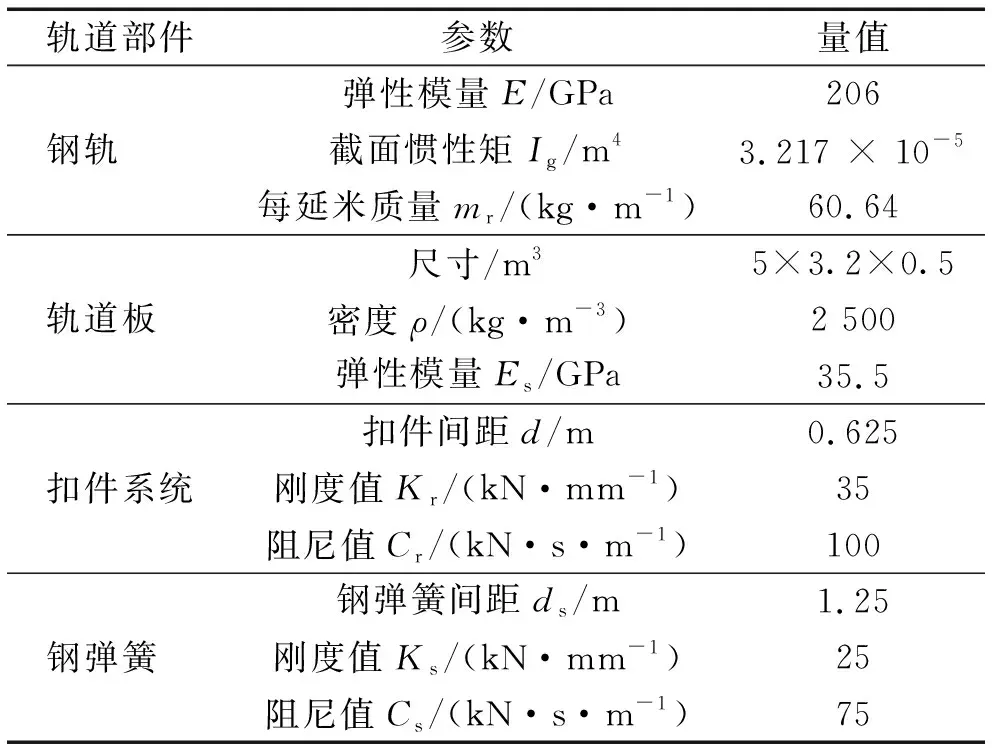
表3 轨道模型参数 Tab.3 Parameters of track model
2.1.3 桥梁系统模型
本文桥梁模型视为多跨简支梁,全桥共8跨,每跨30 m。该桥梁结构模型采用有限单元法建立,其中每个单元节点只考虑垂向沿坐标轴方向的两个线位移和两个角位移,共计四个自由度。单跨桥梁结构具体参数如表4所示。

表4 桥梁模型参数 Tab.4 Parameters of bridge
2.1.4 轨道不平顺模型
车轨耦合模型考虑轨道不平顺的存在,本文采用中国高速无砟轨道谱[17]作为轮轨激励输入,波长范围是1~200 m。
2.2 车辆-轨道-桥梁垂向耦合动力学模型时域解法
车辆系统与轨道系统通过轮轨接触关系实现系统耦合。本文应用Hertz非线性接触理论实现车辆与轨道子系统间的垂向耦合。而桥梁和轨道之间则通过轨道板的垂向约束关系发生相互作用,模型中,两者通过线性弹簧和阻尼连接。车辆-轨道-桥梁系统动力学方程统一形式为
(5)
式中:[M]、[C]和[K]为车辆、轨道和桥梁的质量、阻尼和刚度矩阵;{u}为车辆、轨道和桥梁的广义位移向量;[R]为车辆、轨道和桥梁的广义荷载向量。
本节数值计算采用翟方法[18]积分计算求解车辆-轨道-桥梁系统各自由度的动力响应,积分时长取5×10-5s。
2.3 NES-桥梁动力学模型
为了研究NES装置在桥梁振动激励作用下的动力特性,NES-桥梁动力学模型如图5所示。在“1.1”节的物理模型基础上,桥梁振动主结构采用与“2.1.3”节相同的有限单元法和参数建立,NES结构部分简化为单自由度体系,由质量Ma、弱线性刚度K1、强非线性刚度K3以及阻尼Ca组成。
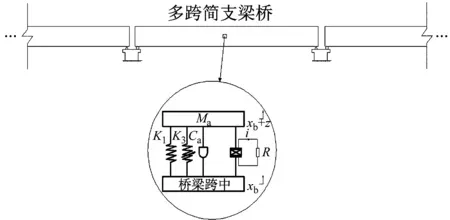
图5 NES-桥梁模型示意图Fig.5 Schematic representation of NES-bridge model
将装置放置于桥梁跨中位置,则NES-桥梁系统动力学控制方程为
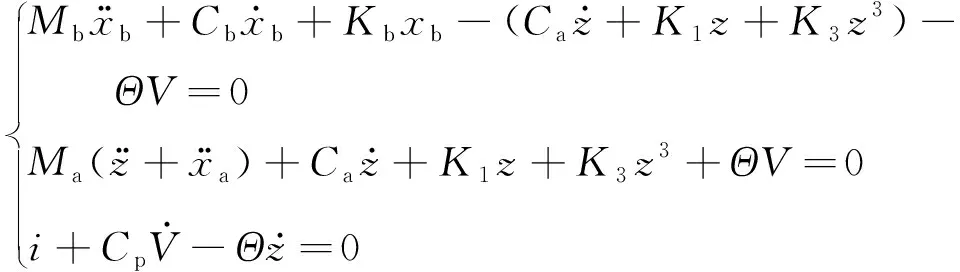
(6)
式中:xb为桥梁跨中单元相对于基础的位移,z为NES质量块相对于桥梁跨中的位移;Ma为NES质量块的质量值;Mb为桥梁质量矩阵[M]中跨中单元的质量值;Cb为桥梁阻尼矩阵[C]中跨中单元的阻尼值;Kb为桥梁刚度矩阵[K]中跨中单元的刚度值;i为电路电流;Θ为机电耦合系数;V为压电悬臂梁的电压输出值;Cp为压电悬臂梁自身电容值。本节通过龙格-库塔法求解非线性动力响应。
3 数值分析
3.1 车线桥动力响应分析
NES的非线性力学特性受外部激励位移影响很大。随着相对位移的增加,NES的刚度急剧增加,此时NES的非线性力学特性表现最为明显,这也是实现NES高效采集能量的重要设计目标。而在桥梁振动中,当结构达到最大位移时,其对应的速度与加速度通常是最小的。因此,为了更加直观地了解分析NES的非线性力学特性,探究基于NES的能量采集装置在桥梁振动中的适用性。本节基于列车-轨道-桥梁垂向耦合动力学模型,分析了不同车速条件下对桥梁跨中最大位移的影响规律。
通过计算得到高速列车以250 km/h、300 km/h和350 km/h通过时,桥梁跨中最大位移分别为1.54 mm、1.78 mm和1.83 mm。说明当桥梁结构确定后,车速对桥梁跨中位移影响不大,这与文献[17]所述不同车速对桥梁跨中垂直位移影响较小的结论相符。
3.2 NES能量采集性能分析
NES能量采集装置相较于传统线性能量采集器能量采集效率更高是由于其与振动主结构能量传递过程具有靶向能量传递的性质,而实现靶向能量传递的关键外部因素之一是位移输入达到激发阈值。因此分析NES装置在桥梁结构的适用性的关键是要在保证桥梁振动主结构与NES装置匹配的情况下,探讨运营条件下的位移激励能否使得NES达到激发阈值。但直接将车线桥模型得到的振动位移作用至NES模型,由于振动输入并不规律,得到的NES位移曲线也不规律,并不能观察出能量传递过程是否达到TET现象。参考文献[8]的研究方法,根据“3.1”节得到的桥梁跨中位移计算结果,考虑到最大载客量等的影响,本节将采用NES-桥梁动力学模型,对桥梁跨中施加不同的初始位移,分别计算分析NES-桥梁模型的动力学特性,具体工况如表5所示。通过保持NES电路负载电阻相同,均为R=200 000 Ω,重点分析桥梁跨中和NES的位移响应以及NES电压输出结果。并在此基础上,基于小波变换得到NES的能量采集时频图,结果如图7~图10所示。
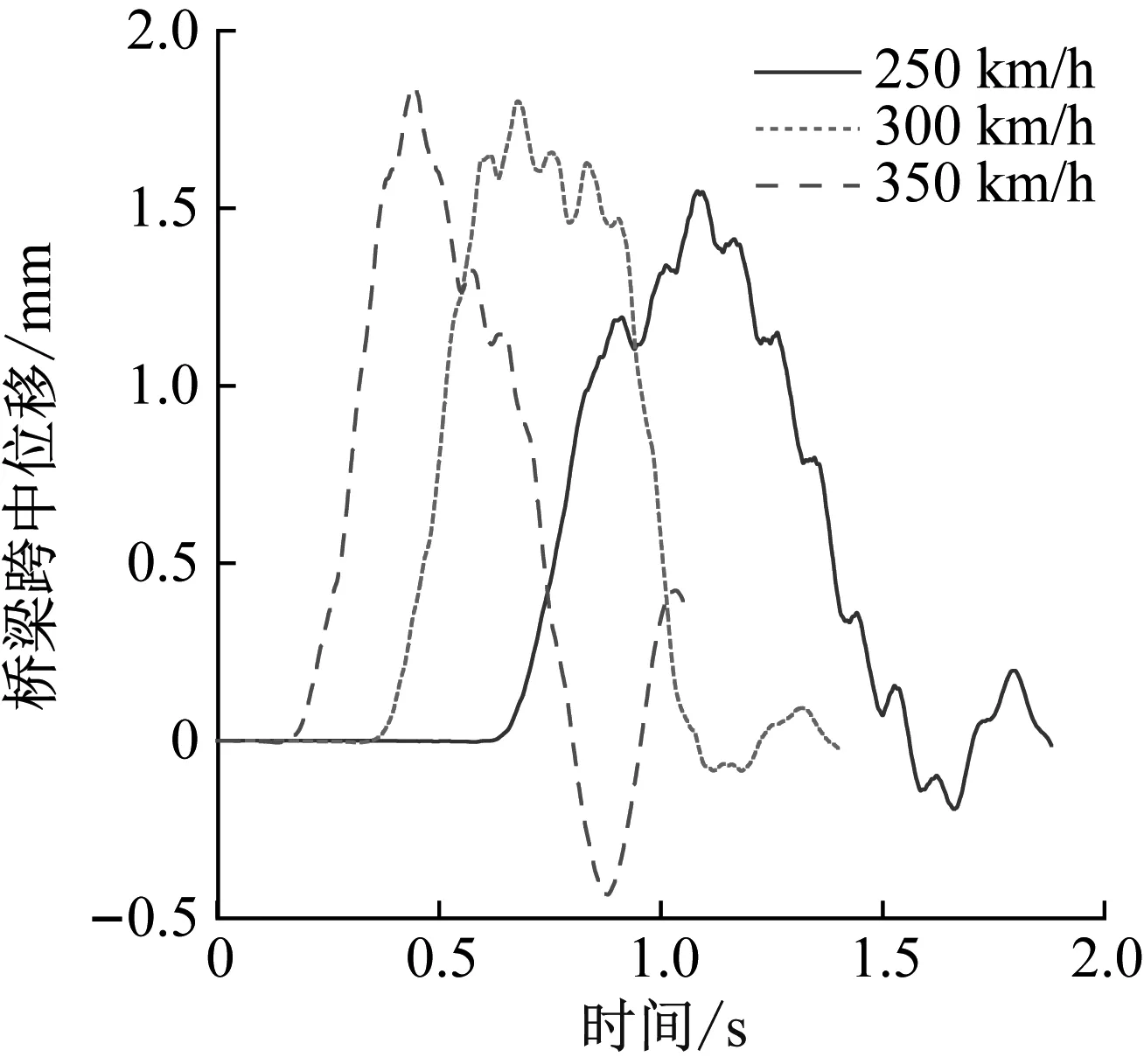
图6 不同车速条件下桥梁跨中位移Fig.6 Mid-span displacement of the bridge under different speed conditions of the train

表5 模型工况Tab.5 Working condition of the model mm
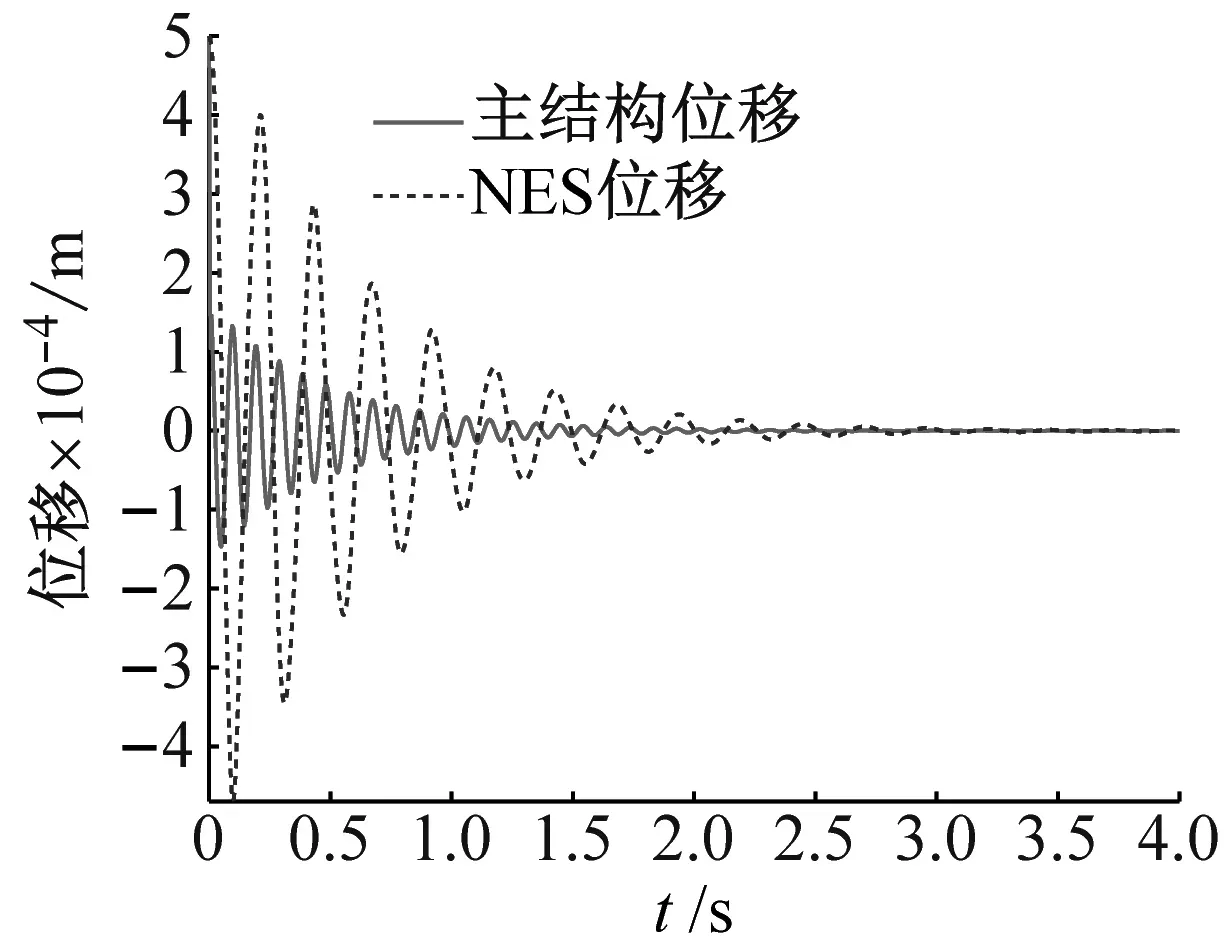
(a) 位移响应
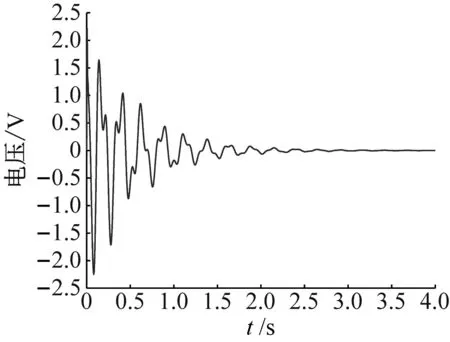
(b) 输出电压
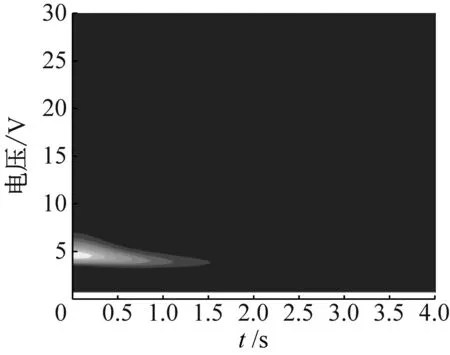
(c) 小波分析图7 初始位移X=0.5 mm的模拟结果Fig.7 Simulation results for X=0.5 mm
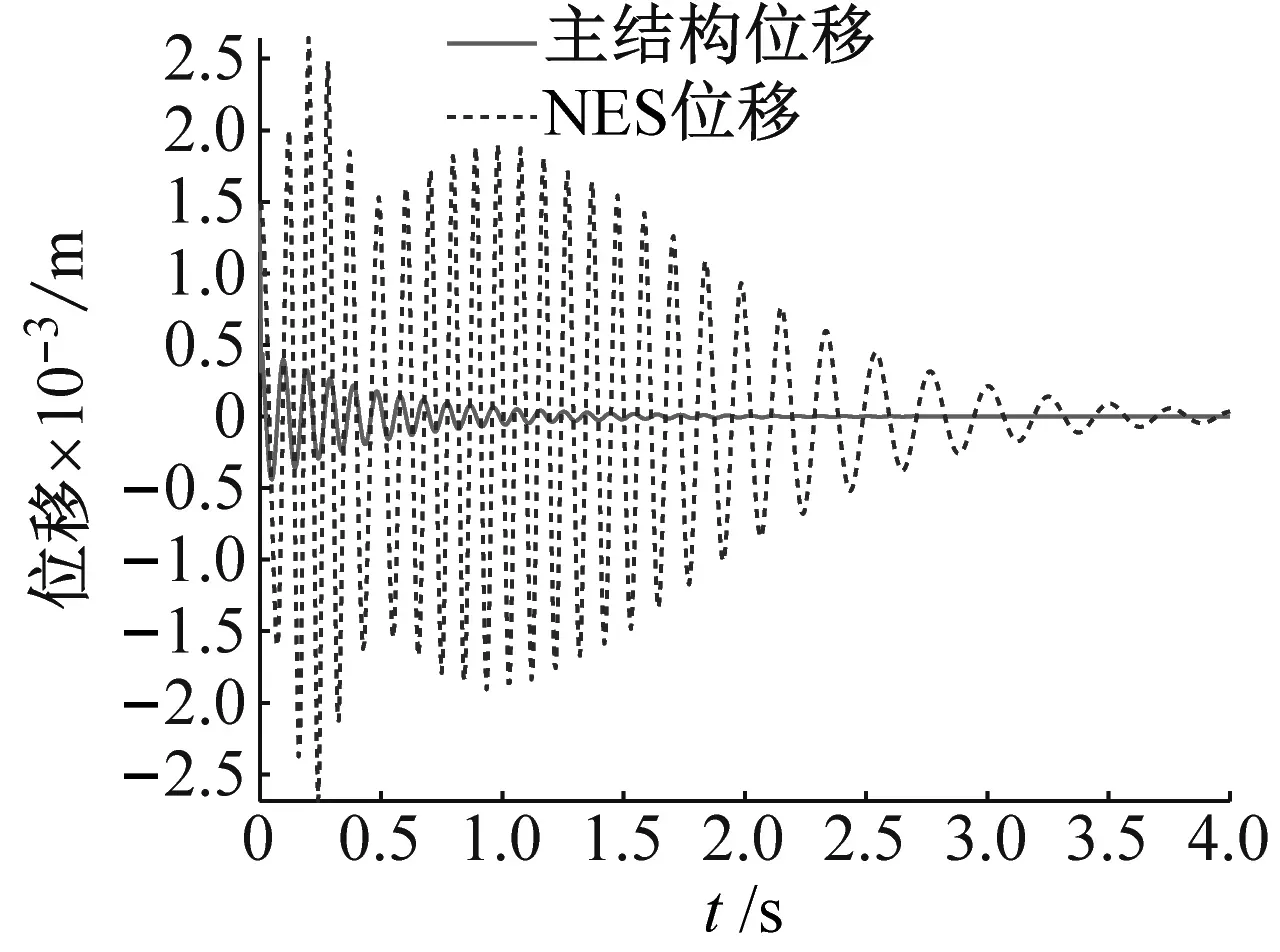
(a) 位移响应
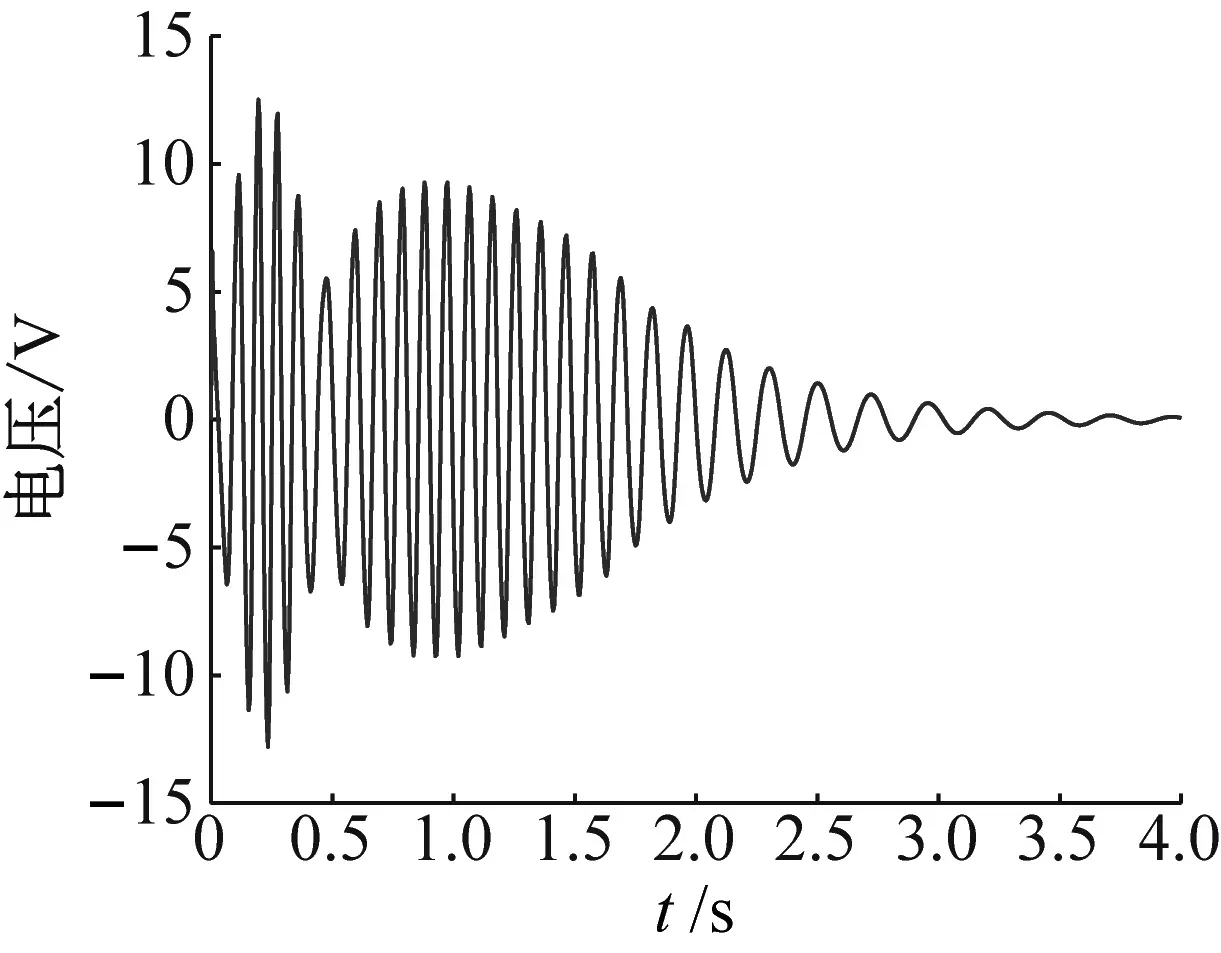
(b) 输出电压
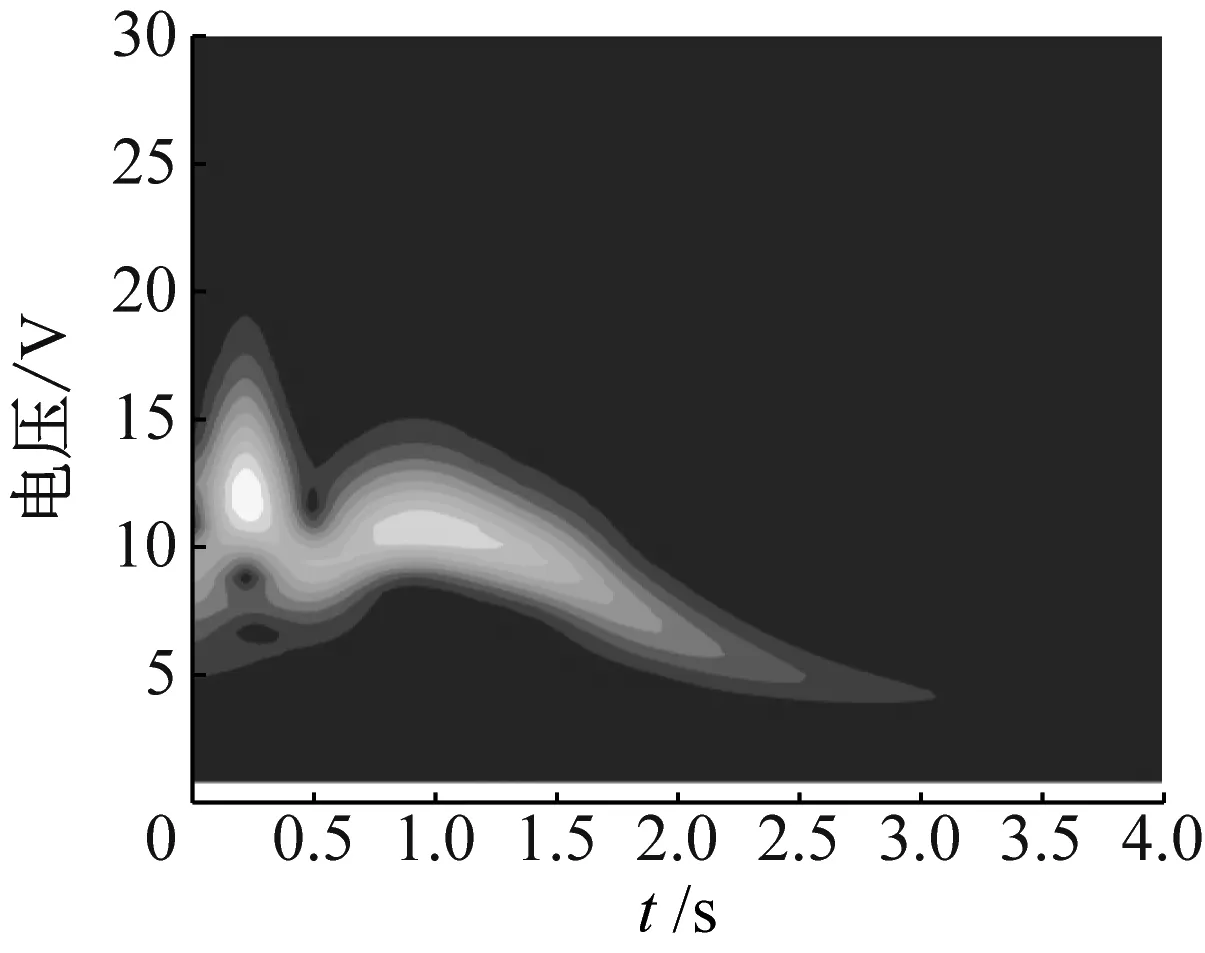
(c) 小波分析图8 初始位移X=1.5 mm的模拟结果Fig.8 Simulation results for X=1.5 mm
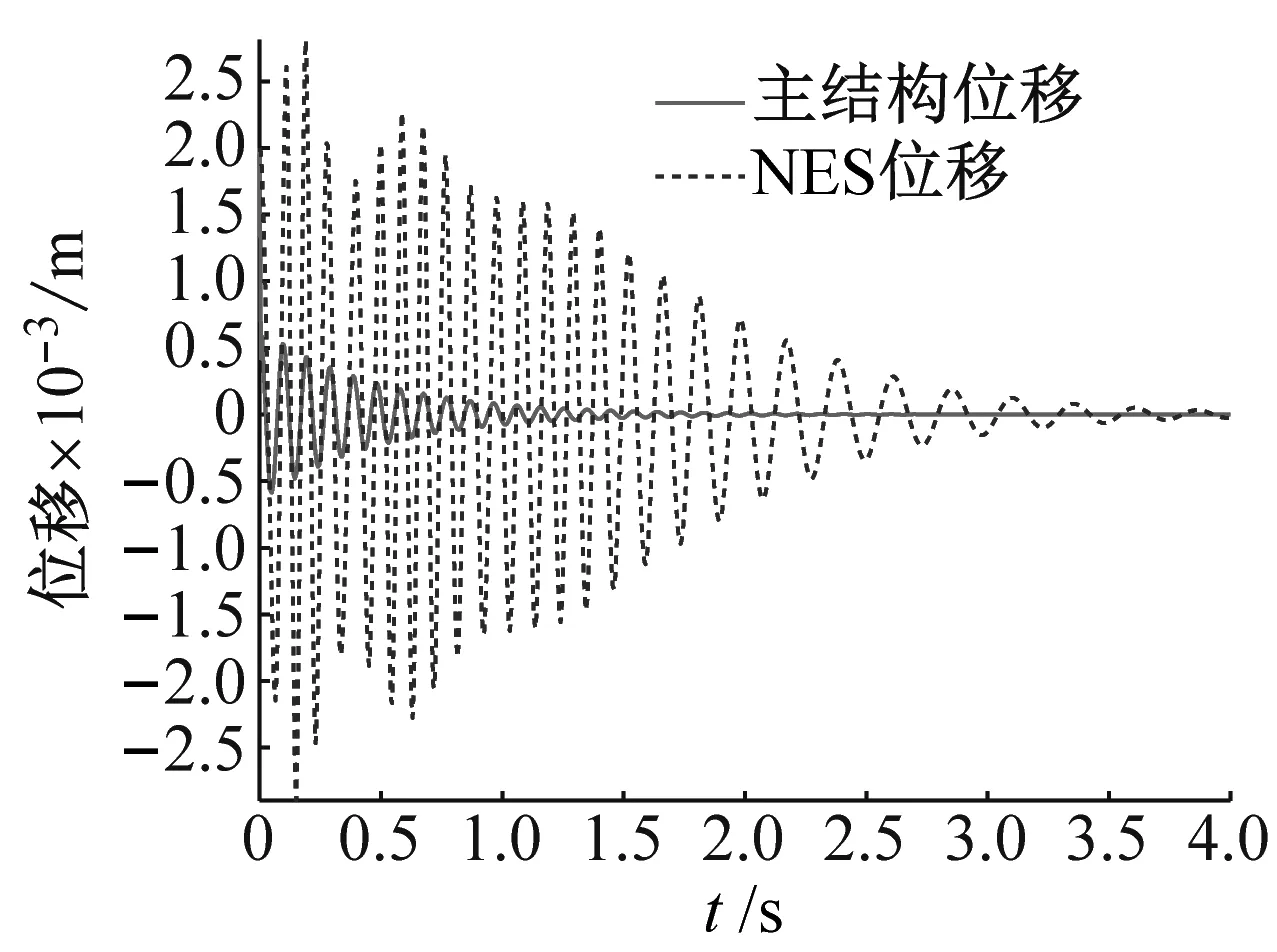
(a) 位移响应
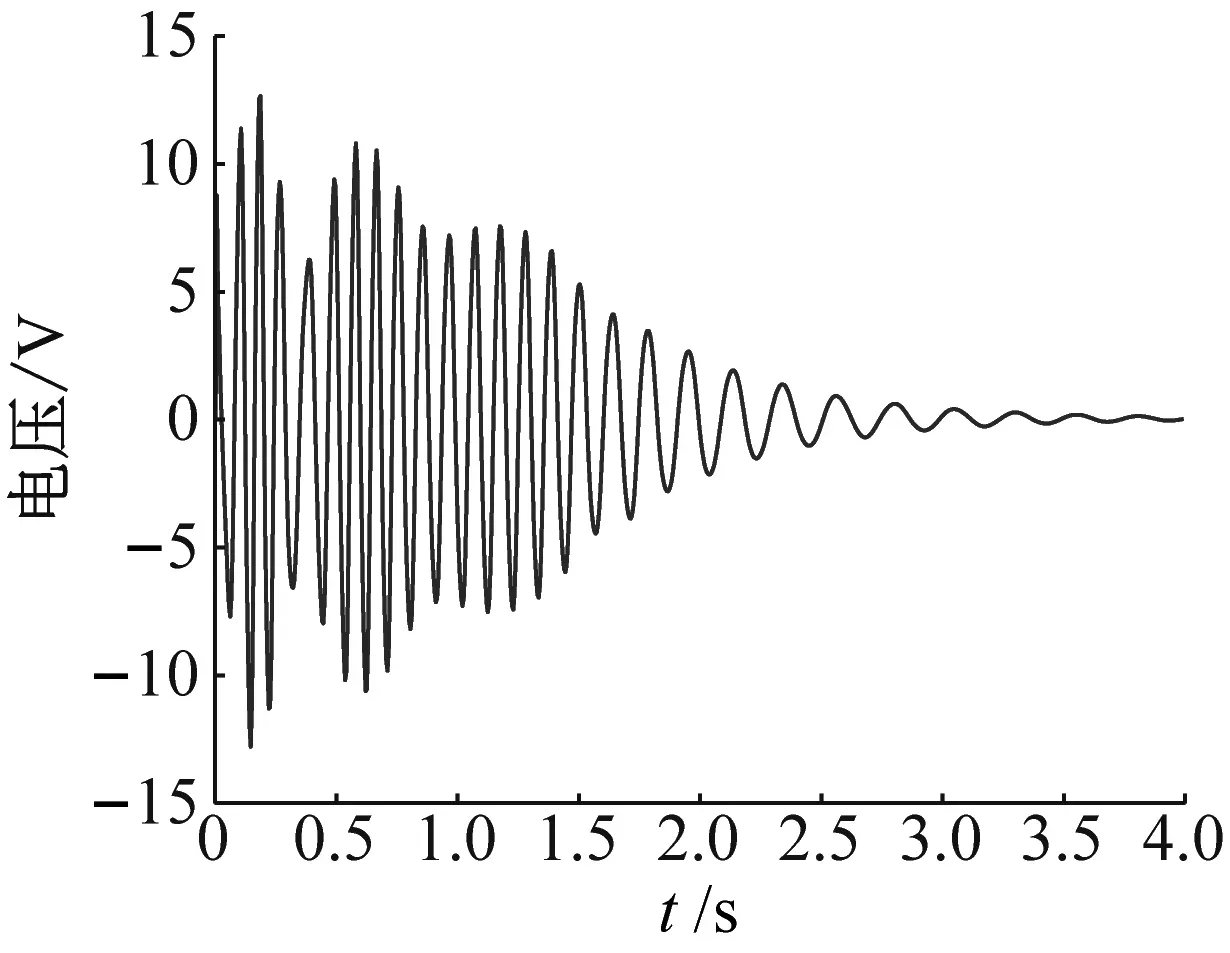
(b) 输出电压
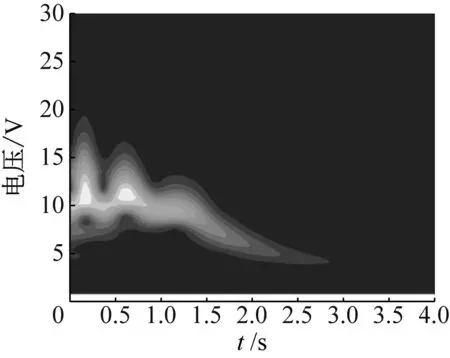
(c) 小波分析图9 初始位移X=2 mm的模拟结果Fig.9 Simulation results for X=2 mm
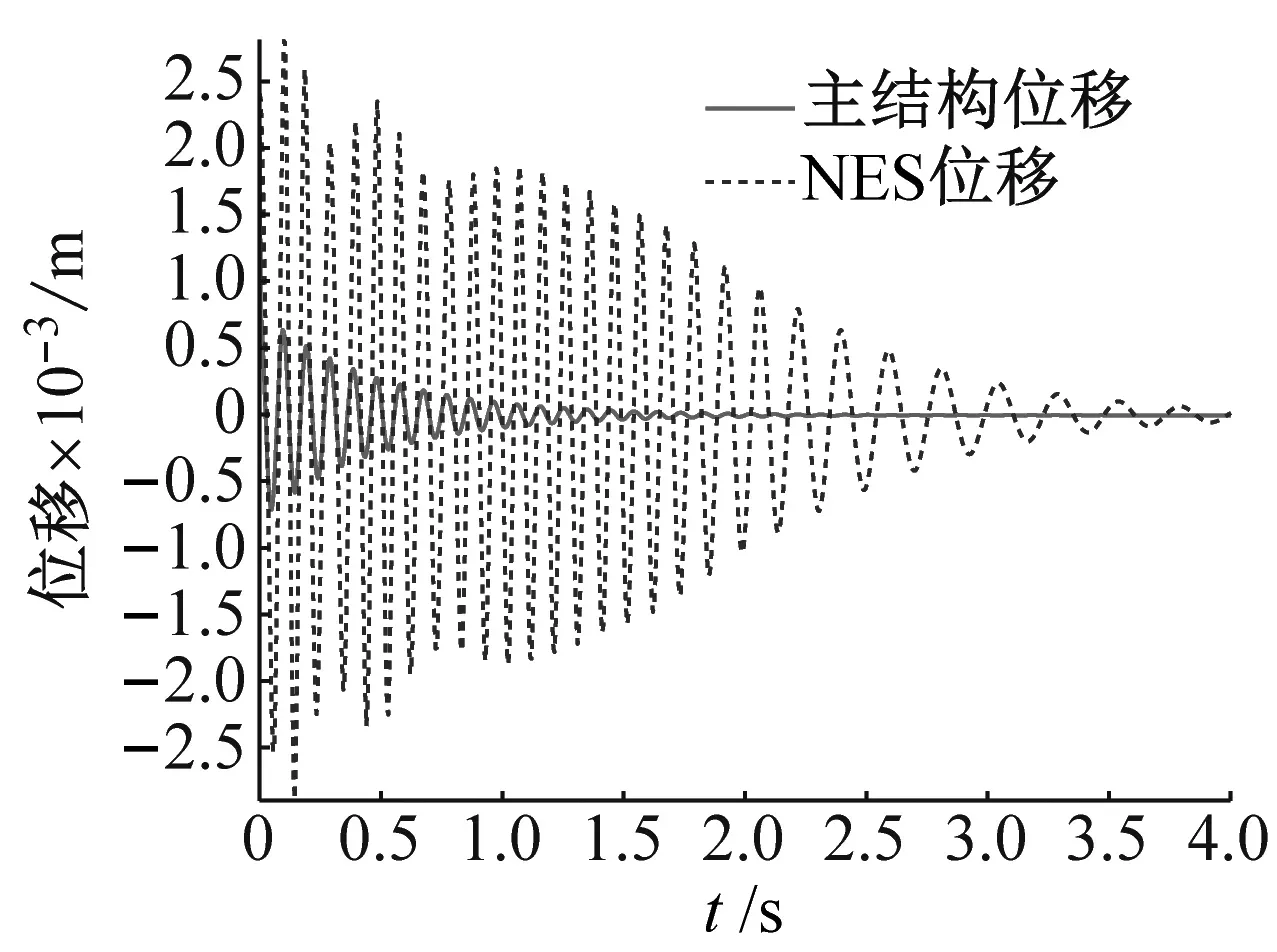
(a) 位移响应
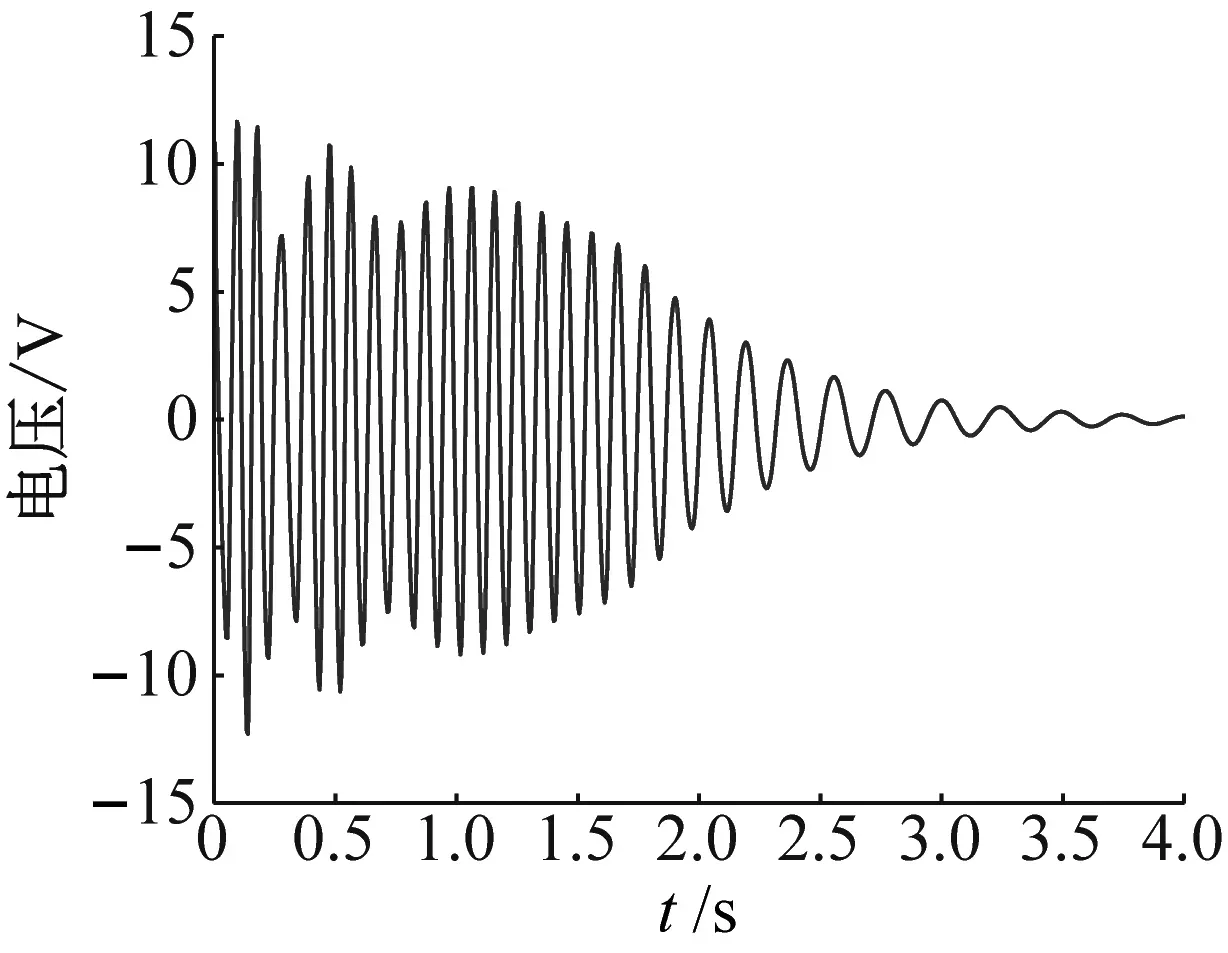
(b) 输出电压
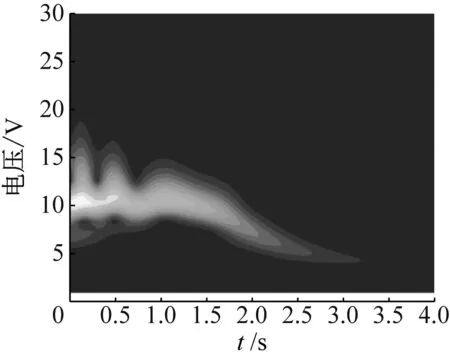
(c) 小波分析图10 初始位移X=2.5 mm的模拟结果Fig.10 Simulation results for X=2.5 mm
工况1将桥梁跨中初始激励设定为较低的水平,X=0.5 mm,NES的位移响应、输出电压及小波分析结果见图7。由图7(a)可知,桥梁与NES装置的位移均较小,且以各自的固有频率振动衰减至0,NES-桥梁系统内没有发生内共振,TET过程并未发生,整个振动衰减过程中的大部分机械能均在桥梁结构内部通过其自身阻尼耗散,并未有效地传递并停留于NES装置中。从图7(b)可知,初始的电压峰值较低,为2.3 V,且经过2 s快速衰减为0,与NES的振动位移规律一致。从图7(c)的小波分析结果中也可知,NES装置一直在其自身固有频率5 Hz附近做自由衰减振动,未出现与桥梁结构的共振。因此,该组由于初始激励能量较小,未能达到触发TET发生的能量阈值,能量采集效果一般。
工况2将桥梁跨中初始激励提高至X=1.5 mm,结果见图8。由图8(a)可知,NES与桥梁结构的振动呈现出1∶1内共振且持续时间约t=0.5 s。系统在初始时刻出现了短暂的非线性拍现象,随后NES在约t=2 s之后以固定的频率振动一段时间,但与桥梁振动不同相。在桥梁振动位移接近0时,NES振动开始衰减且振动频率也减小;NES在该量级的初始能量激励下出现了TET,能量从主结构单向不可逆地传递至NES中;NES装置在振动初期对桥梁振动能量产生了吸附作用,使得能量在短时间内快速转移并固定于NES中;但由于初始能量的量级仍然较小,TET现象仅仅持续了不足1 s。从图8(b)可知,电压与NES振动位移同步,整个振动衰减过程中的电压幅值均显著高于X=0.5 mm时系统内压电悬臂梁的输出电压幅值。图8(c)可知,NES位移的小波分析图谱,NES在最初的t=0.5 s内的振动出现了非线性拍现象,随着之后TET的结束,由主结构单向传递至NES的能量固定并耗散于NES之中,且NES的振动频率逐渐由桥梁结构一阶固有频率10 Hz左右过渡至其自身的固有频率5 Hz。因此,该初始能量的量级已达到激发阈值,出现TET现象,具有较好的能量采集效果,但该持续时间较短。
在工况3中,进一步将桥梁结构跨中的初始激励提高至X=2.0 mm,结果见图9。从图9(a)可知,桥梁结构与NES的振动频率和相位在振动过程的前t=0.7 s内均达到同步,系统进入1∶1共振捕获阶段,桥梁结构中的振动能量单向不可逆地传递至NES装置中。由图9(b)可知,压电悬臂梁的输出电压仍然与NES的振动位移同步。相较上组,电压幅值有所提高。同时,由图9(c)可知,小波分析NES在初期的t=0.7 s内出现了更强的非线性拍现象,在t=1.5 s时,NES的振动频率开始减小,此时NES装置与桥梁结构的能量传递不再具有单向不可逆性质。该组初始能量达到激发阈值,触发了TET过程。对比工况2,该组由于初始激励更大,系统内共振时间更长,进一步发挥了NES非线性的优势,能量采集效果更好。
当桥梁跨中初始激励达到2.5 mm时,见图10。从图10(a)可知,桥梁结构与NES装置的振动在前t=1 s内相位完全同步,并具有相同的振动频率。此时初始激励达到阈值,系统触发TET过程;且与工况3相比,系统1∶1内共振持续时间更长。从图10(b)可知,电压曲线与位移曲线有较好的吻合,随着TET的增强,电压幅值进一步小幅增加,且高电压输出时间更长。从图10(c)可知,相比于工况3,NES振动初期的非线性拍现象减弱,系统更早进入TET过程。NES的振动频率在前t=1.5 s内维持在10 Hz附近,随后,振动变慢,振动频率逐渐减小至自身固有频率。对比前几个工况,进一步提升初始激励,TET现象会更早出现且持续时间更长,与此同时,电压输出时长也同步增加,能量采集效率更高。
通过以上分析可以得出,当初始激励不同时,NES-桥梁系统产生了不同的能量传递现象,只有当初始激发能量达到某一临界值时,系统才会触发TET过程,且该过程随着初始能量的增大而增强。
对于本文所述的NES-桥梁系统而言,由“3.1”节及“3.2”节分析可知,该铁路桥梁在列车荷载工况作用下的桥梁跨中位移能够使得NES达到TET激发阈值。且对比工况1与其他工况可以看出,TET传递过程的出现显著提高了能量采集效率,这也是相较线性能量采集装置,非线性能量采集装置的优势之一。由文献[4]可知,目前大多数低功耗或超低功耗商用无线传感器的功率要求在毫瓦范围内,按照本文所研究的NES能量采集装置目前的尺寸来说,NES在达到TET传递条件下输出的功率能够达到毫瓦级别,转换的电能能够满足一部分低功耗传感器的供电需求。而且,对于实际工程应用,能够根据实际桥梁结构的参数调整NES的结构尺寸以及压电悬臂梁的型号和尺寸,以增大能量采集的输出功率。在桥梁结构这种振动随机且复杂的环境中,非线性能量采集装置能够发挥非线性优势,更为高效地采集能量,为桥梁无线传感器节点供电,对绿色桥梁监测管理系统的建立与发展有实际价值。另外,根据压电转换器在非线性振动激励作用下产生的压电效应,结合相应的触发集成电路,可在采集能量的同时,对桥梁结构进行位移监测。即通过优化NES结构设定触发TET现象的阈值,实现桥梁因结构劣化等因素出现较大位移时,装置能自动触发预警的目的。
4 结 论
本文测试与表征了一种基于NES的压电式振动能量采集装置,并通过仿真理论分析,探讨了该NES装置在铁路桥梁上的适用性及能量采集效果,具体结论如下:
(1) 相较于传统的线性振动能量采集装置,基于NES的能量采集装置由于自身的极弱线性刚度和极强非线性刚度特性而具有宽频且高效的能量采集效果,对于处在实际环境中受到随机振动激励下的桥梁结构较为适用。
(2) 通过建立列车-轨道-桥梁垂向耦合动力学模型,计算分析可知,当桥梁结构确定后,本文所用简支梁桥在列车荷载激励作用下跨中最大位移在1.5~2.0 mm。此外,在NES-桥梁动力学数值模型中,通过将桥梁跨中最大位移作为初始激励输入分析得到,只有当初始位移达到一定阈值时,NES-桥梁系统中才会出现TET现象。如果初始能量低于该阈值时,NES装置与桥梁结构以各自的固有频率振动,TET未能被激发,即NES的能量采集效率一般。另一方面,当初始能量达到阈值时,NES-桥梁系统将出现1∶1内共振,即桥梁振动能量单向不可逆地传递到NES装置中,输出电压也大幅提高。进一步地,当初始能量高于阈值时,随着初始位移的增大,可以观察到更强且持续时间更长的TET过程。
(3) 对于桥梁振动能量采集而言,基于NES的能量采集装置能够在合适的桥梁振动激励下达到激发TET过程的位移阈值,可以结合自身非线性特性的优势,发挥更好的能量采集性能。并且,根据该装置具有位移激发阈值的特性,可根据实际工程所需,通过结合相应的触发集成电路实现对桥梁结构的位移监测预警,因此在桥梁工程具有良好的应用前景。
