万向接轴附加动态弯矩下板带轧机垂扭耦合振动特性研究

侯东晓， 陈善平， 方 成， 时培明， 王新刚

(1.东北大学秦皇岛分校 控制工程学院，河北 秦皇岛 066004； 2.燕山大学 电气工程学院,河北 秦皇岛 066004)

轧制板带材广泛应用于众多工业生产领域中，随着对轧制生产效率和产品质量要求的提高，对轧制速度及轧制过程的稳定性要求也变得越高，但由此导致的轧机振动问题也随之暴露。针对轧机振动问题，研究人员在轧机振动新模型与理论探索等方面进行了深入研究。刘浩然等[1]研究了轧件弹塑性滞后非线性变形对轧机垂直系统振动特性的影响。刘飞等[2]研究了液压缸非线性弹性力和非线性摩擦力约束下的轧机辊系振动行为。高崇一等[3]研究了多间隙存在时对轧机传动系统扭矩放大系数的影响。Heidari等[4]研究了非定常润滑对冷轧带钢颤振的影响。

随着研究深入，轧机耦合振动行为也逐渐引起研究人员的关注。Zeng等[5]采用Hopf分岔代数判据分析了非线性摩擦下的轧机垂直-扭转-水平耦合动力学模型的稳定域，并构造相应反馈控制器抑制轧机的不稳定振荡行为。刘彬等[6]建立了水平方向的轧件-轧辊耦合振动模型，研究了该耦合模型的非线性振动特性。

轧机万向接轴倾角对轧机振动也有着一定的影响。纪志强[7]研究了厚板轧机万向接轴倾角产生的附加弯矩与轧机刚度和轧制力之间偏差关系。王辉等[8]研究了万向接轴倾角对热连轧机工作辊横向振动的影响。Shi等[9]研究了万向接轴倾角影响下轧机主传动系统非线性扭振特性，时培明等[10]在此基础上进一步研究了万向接轴倾角对多自由度轧机主传动系统非线性非主共振扭振特性的影响。闫晓强等[11]根据现场实验数据指出轧机万向接轴存在质量偏心和倾角会导致扭转振动与弯曲振动的耦合。

目前大多数学者的研究中只考虑万向接轴倾角单独对轧机传动系统扭振或水平振动等单一系统振动的影响。实际上万向接轴随着转速变化，接轴两端会存在随转速变化的附加动态弯矩。轧辊端动态弯矩既受传动系统转速影响，又影响垂直方向的轧辊振动，其与垂直和扭转方向振动都密切相关，但对该方面尚未见深入研究。

为此，本文考虑轧机万向接轴倾角产生附加动态弯矩的影响，建立轧机垂直-扭转耦合振动模型。运用奇异性理论研究了轧机垂扭耦合模型的分岔特性。并通过仿真分析了垂直和扭转方向动态轧制参数、扭转刚度、扰动力幅值等参数变化对轧机垂直和扭转方向主共振幅频曲线的影响，这为进一步抑制或控制轧机振动提供了理论参考。

1 万向接轴倾角影响下附加动态弯矩

轧机在轧制过程中，万向接轴安装采用“Z”型布置，如图1所示。此时电机输入端和轧辊输出端处于同一平面，且输入轴和输出轴平行，前后轴线夹角相等。图1中，θ1和θ2分别为电机端和轧辊端的扭转角度；α为万向接轴倾角，M1为电机端扭矩，M2为万向接轴扭矩，M3为轧辊端扭矩。ψ1和ψ2分别为万向接轴的输入和输出扭转角度。

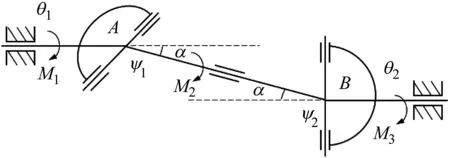
图1 万向接轴受力示意图Fig.1 Schematic diagram of universal joint force model

根据轧机传动系统中主动轴与从动轴的运动学关系为[12]

tanψi=tanθicosα，i=1,2,…

(1)

电机与输入轴的关系为

(2)

输出轴与轧辊的关系为

(3)

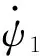
当万向接轴两端节叉平面处于同一平面时，电机轴转过θ1角度，由式(2)得到万向接轴上扭矩为

(4)

套筒轴上面的附加弯矩为

(5)

由图1可知，万向接轴A叉和B叉在同一平面，A叉比B叉超前90°，即：

θ2-90°=θ1

(6)

所以式(5)可以写成

(7)

结合式(2)式(3)将式(7)分解得套筒上面垂直附加动态弯矩为

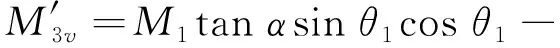
M1sinαcosαsinθ1cosθ1

(8)

2 板带轧机垂直-扭转耦合振动动力学模型

考虑轧机倾角产生的附加动态弯矩影响，可得到板带轧机垂直-扭转耦合振动模型，如图2所示。图2中，ω为电机的角频率；m为上部辊系的等效质量；K为接轴的扭转刚度，K1为上辊系与上横梁间的等效刚度；C为万向接轴的结构阻尼，C1为上辊系与上横梁间的等效阻尼；J1和J2分别为电机和轧辊的等效转动惯量；F为动态轧制力；T为上辊系动态轧制力矩；y为工作辊垂直位移。

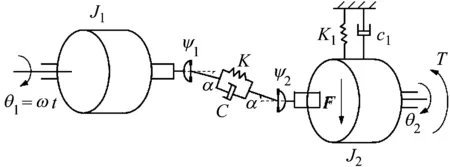
图2 板带轧机垂直-扭转耦合振动模型Fig.2 Vertical torsion-coupled vibration model of strip rolling mill

由图2可得到板带轧机垂直-扭转耦合振动方程

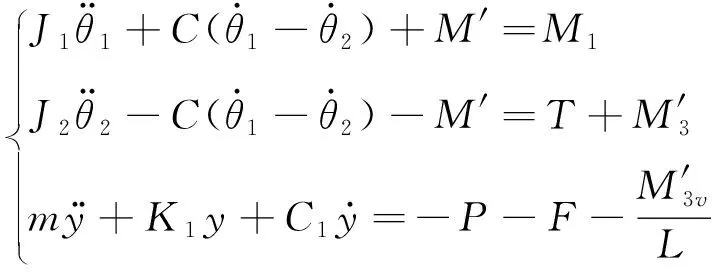
(9)

式中：M′为接轴的弹性力矩;P为外部扰动;L为工作辊轴承座中心间的距离。

式(9)中动态轧制力F采用如下形式[13]

F=F11+ΔF

(10)

式中:F11为稳态轧制力;ΔF为轧制力动态变化量。

(11)

动态轧制力矩T：

T=T11+ΔT

(12)

式中:T11为稳态轧制力矩;ΔT为轧制力矩动态变化量。

(13)

其中

M′=K·λ2(θ2)(ψ2-ψ1)=KF(θ2,t)

(14)

将式(1)、式(2)和式(3)代入(14)得

(15)

由于转角差Δθ较小，因此可假设：1-sin2αsin2(ωt-Δθ)=1-sin2αsin2(ωt),tan Δθ=Δθ,tan(ψ1-ψ2)=tan(ψ1-ψ2)。

所以式(15)可简化成

(16)

此时式(9)可以写成

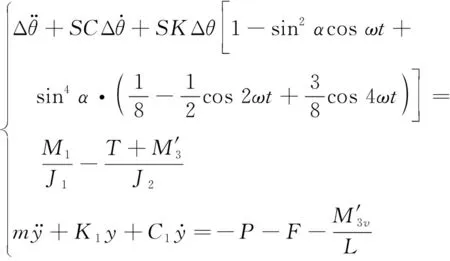
(17)

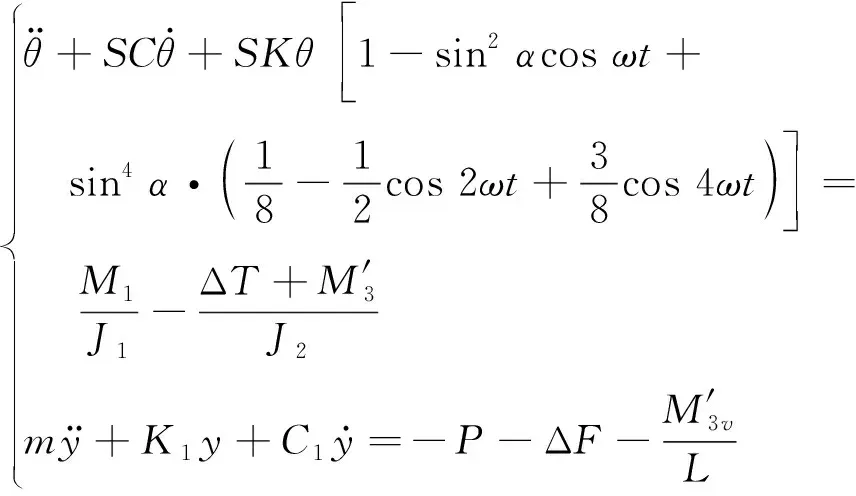
(18)

3 板带轧机垂直-扭转耦合振动方程主共振响应求解

假设轧机在轧制过程中受到周期性的外部扰动即P=F0cosωt，令：

ω1=[(K1+a9)/m]1/2，ω2=(SK)1/2，γ1=1/m，γ2=-1/J2，η1=M/2L，η2=M1/J1，ζ1=(C1+a17)/m，ζ2=(CSJ2+b2)/J2。

所以式(18)可写成

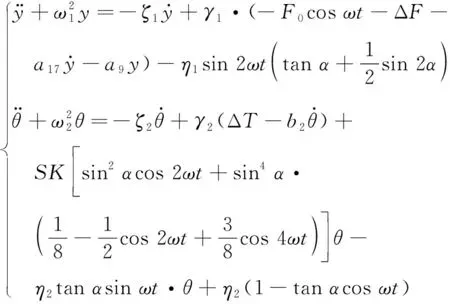
(19)

设式(19)为弱非线性系统，引入小参数ε，式(19)可写成

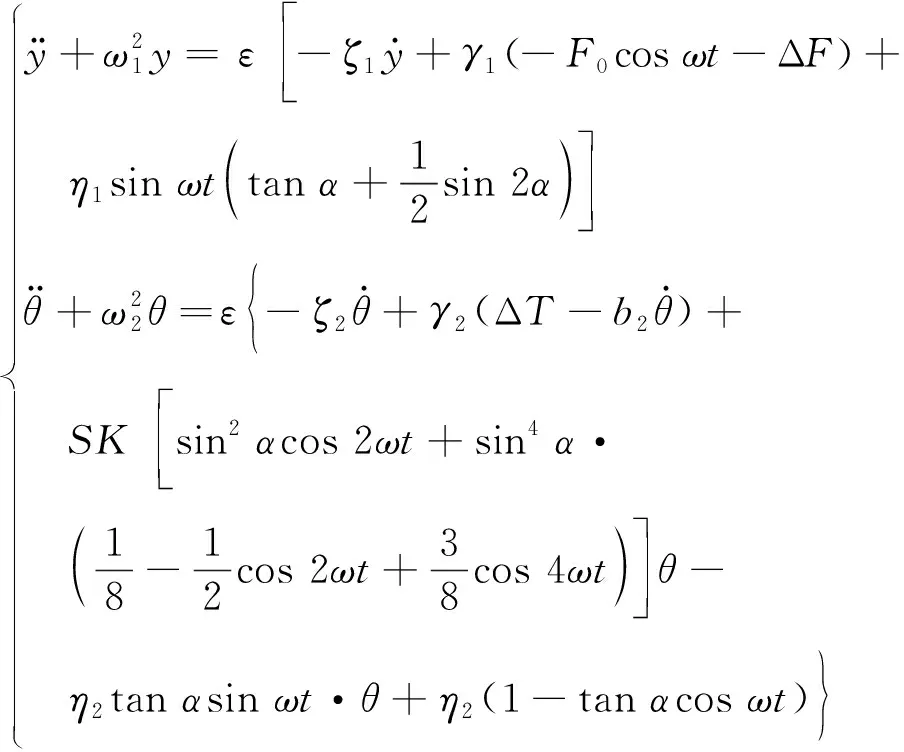
(20)

采用多尺度法，令T0=t，T1=εT0，假设系统具有如下的一次近似解

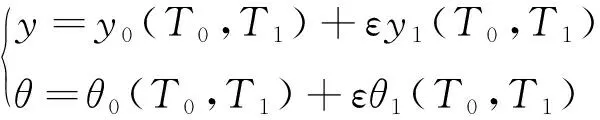
(21)

将式(21)代入式(20)中，通过比较ε0的系数可得

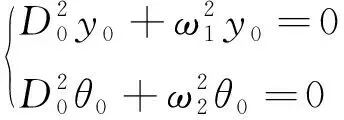
(22)

比较ε1的系数可得：

(23)

式中，Di=∂/∂Ti(i=0,1)，Di为偏微分算子。

设式(22)的解为

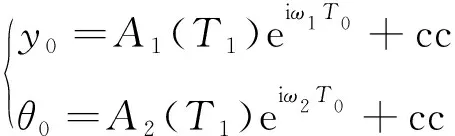
(24)

式(24)中cc表示前一项的共轭项，将式(24)代入式(23)，考虑主共振情况，令ω=ω1+εσ，σ为调谐参数，消除永期项得

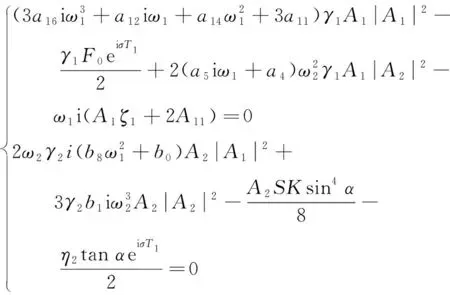
(25)

引入A1和A2的极坐标形式

(26)

将式(26)代入式(25)，分离虚部和实部，令τ=σT1-β1：

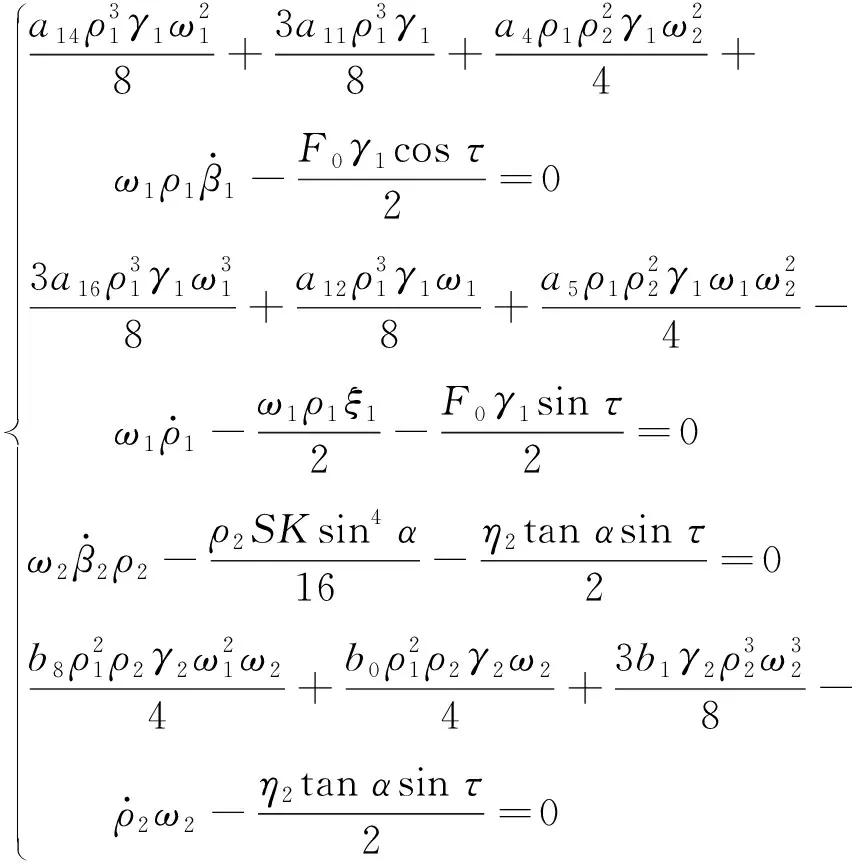
(27)

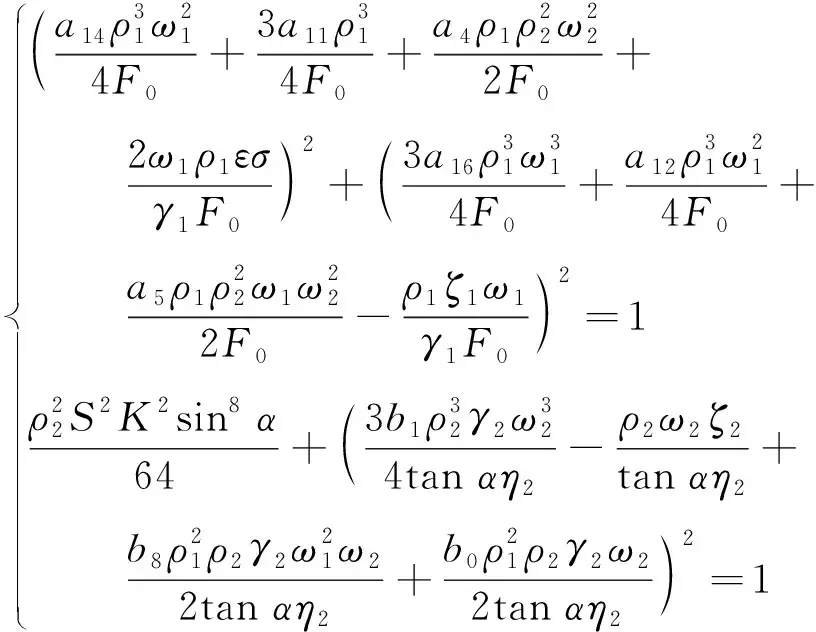
(28)

4 板带轧机耦合振动系统奇异性分析

轧机在实际轧制过程中，或多或少会存在某些未知因素会使轧机振动参数和结构参数出现偏差，因此可采用奇异性讨论参数变化对轧机振动形态的规律。

将式(28)合并化简，并在稳态点ρ2=ρ0处展开，略去高次项可得系统的分岔方程

(29)

其中

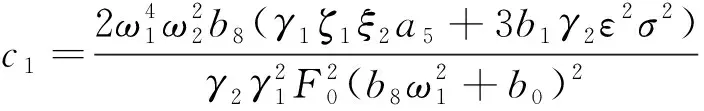
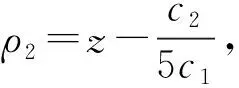
z5+d1z3+d2z2+d3z+λ=0

(30)

其中

讨论不同参数空间在投影面上转迁集以及静态分岔行为的3种情况。

(1) 当d1=0时，z5+d2z2+d3z+λ=0，

根据转迁集定义，可得如下转迁集：

分岔点集B=∅；

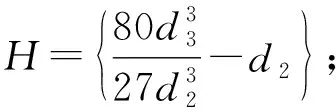
双极限点集D=∅；

系统的转迁集∑=B∪H∪D。

此时系统的转迁集及其划分的不同区域中分岔拓扑结构图，如图3所示。

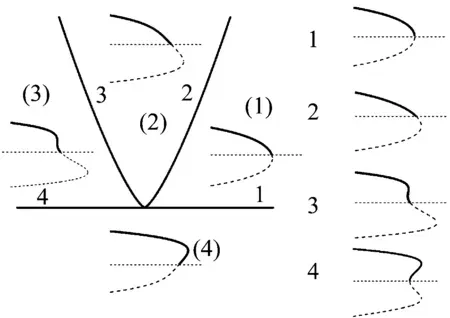
图3 d1=0系统转迁集和分岔拓扑结构图Fig.3 Transition set and bifurcation topology diagram of parametric system when d1=0

(2) 当d2=0时，z5+d1z3+d3z+λ=0，转迁集为：

分岔点集B=∅；

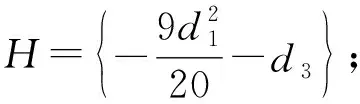
双极限点集D=∅；

系统的转迁集∑=B∪H∪D。

系统的转迁集及分岔如图4所示。

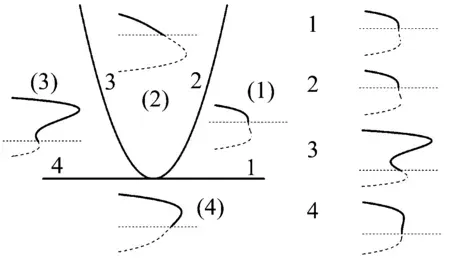
图4 d2=0系统转迁集和分岔拓扑结构图Fig.4 Transition set and bifurcation topology diagram of parametric system when d2=0

(3) 当d3=0时，z5+d1z3+d2z2+λ=0，转迁集为：

分岔点集B=∅；

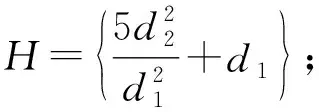
双极限点集D=∅；

系统的转迁集∑=B∪H∪D。

系统的转迁集及分岔如图5所示。

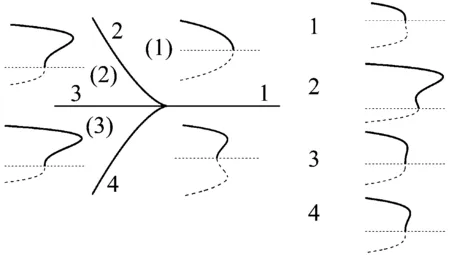
图5 d3=0系统转迁集和分岔拓扑结构图Fig.5 Transition set and bifurcation topology diagram of parametric system when d3=0

由图3、图4、图5可知，转迁集将整个平面划分成4个区域，在不同的区域中系统具有不同的分岔曲线，其中图3中区域(1)、图4中区域(2)、图5中区域(1)是稳定的，其他区域振动幅值都出现了跳跃现象，因此可以通过调节d1、d2、d3的参数，来抑制轧机振动。

5 数值仿真分析

采用某厂1 780四辊板带轧机实际参数：m1=1.44×105kg,K=2.41×108N·m/rad,K1=2.25×1010N/m,J1=13 170 kg·m2,J1=983 kg·m2,C=339 N·s/m,C1=1.04·105N·s/m,a0=8.282×109,a1=406.309,a2=6.265×105,a3=-2.001×104,a4=3.833×106,a5=-394.080,a6=-1.982×108,a7=1.511×104,a8=129.047,a9=-3.842×106,a10=-7.993×109,a11=-2.721×1013,a12=3.254×1011,a13=9.776×107,a14=8.721×105,a15=-2 870.228,a16=-14.277,a17=-2.335×105,a18=1.011×1010,b0=7.233×108,b1=6.748,b2=1.494×104,b3=-377.393,b4=9.397×104,b5=-6.584,b6=-6.879×106,b7=285.587,b8=2.170,b9=-8.562×104,b10=-3.375×108,b11=1.454×1012,b12=2.949×1010,b13=2.689×106,b14=1.847×104,b15=-54.249,b16=-0.242,b17=-5 061.281,b18=-3.370×108。

轧机倾角α变化时轧机垂直扭转方向的幅频曲线,如图6所示。

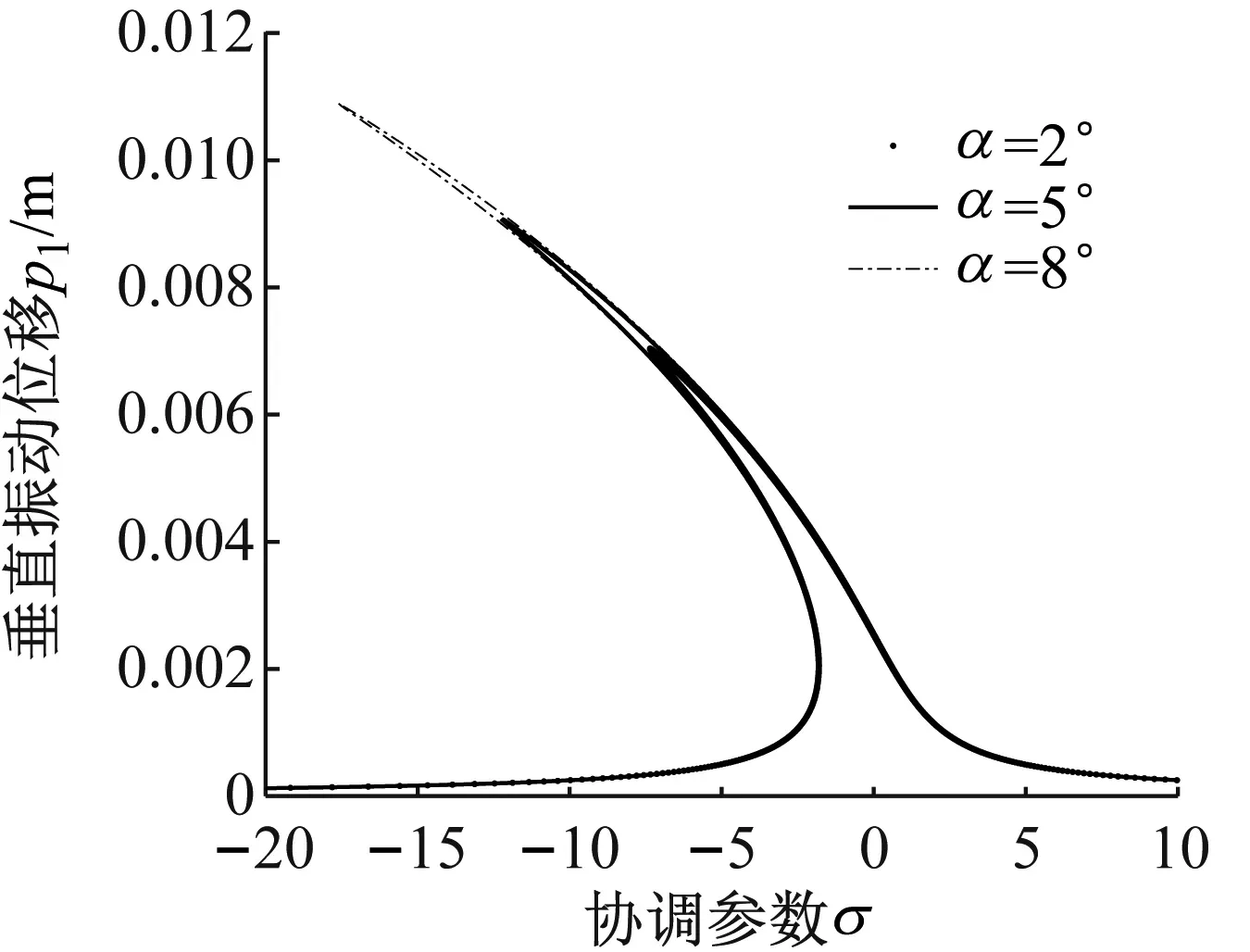
(a) 垂直方向

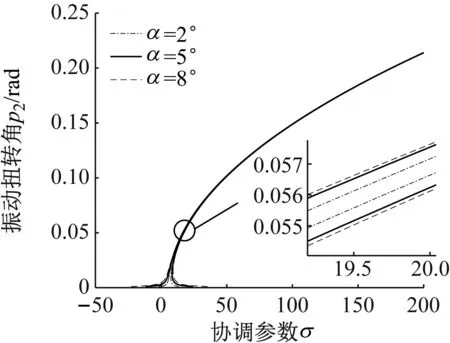
(b) 扭转方向图6 α变化时垂直和扭转方向主共振幅频曲线Fig.6 The curve of primary resonance amplitude-frequency in vertical and torsional directions with different α

由图6(a)可知，轧机倾角α的变大会造成垂直方向主共振幅值的增大且幅频曲线跳跃现象越来越明显。同时由图6(b)可知，在考虑轧机接轴条件下的轧机垂扭主共振幅频曲线是两条永不相交的曲线，当接轴倾角逐渐增大，两条曲线的间距也在增大。

当轧机接轴倾角α一定，动态轧制力系数a11改变时耦合系统垂直扭转方向的幅频曲线,如图7所示。

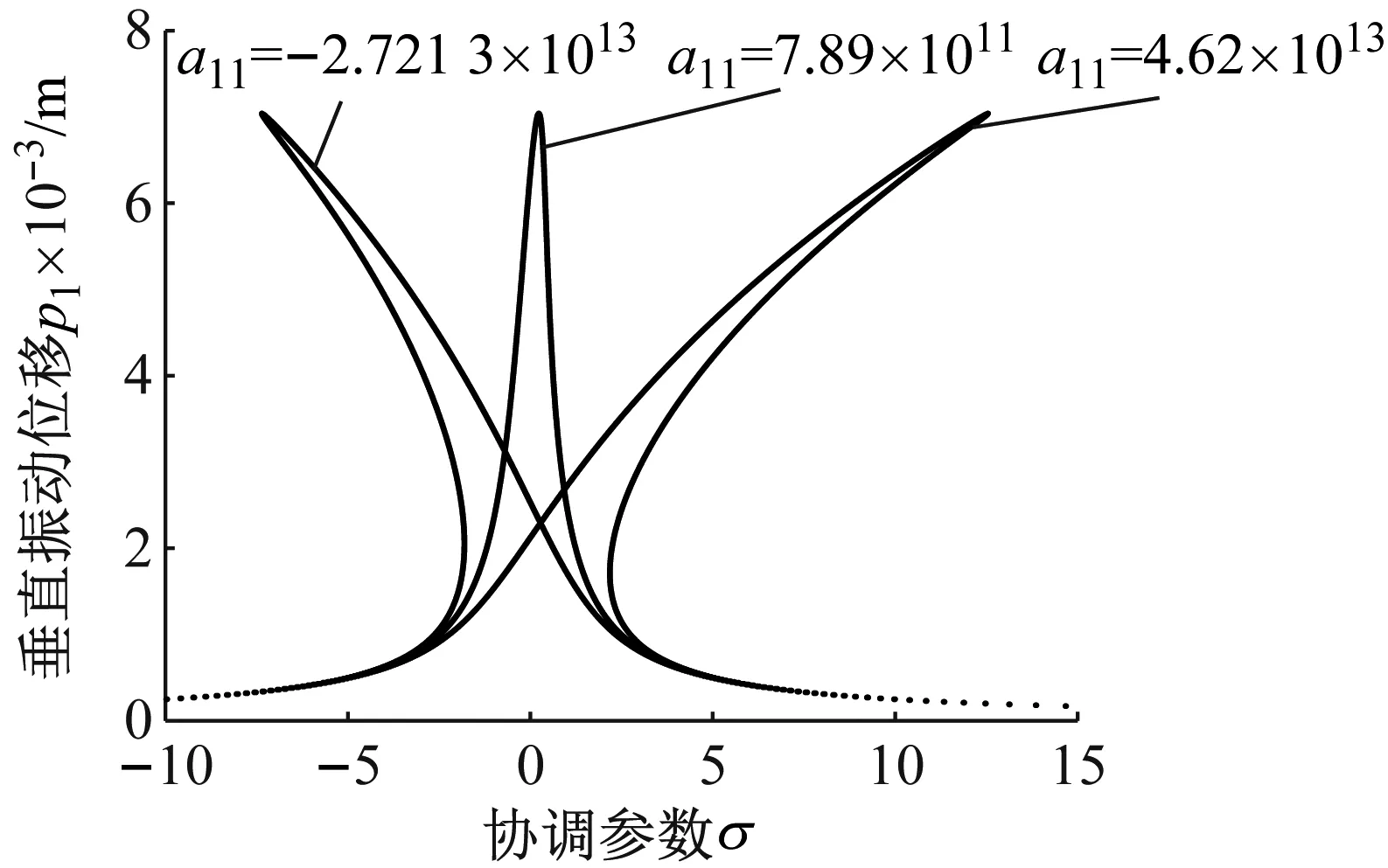
(a) 垂直方向

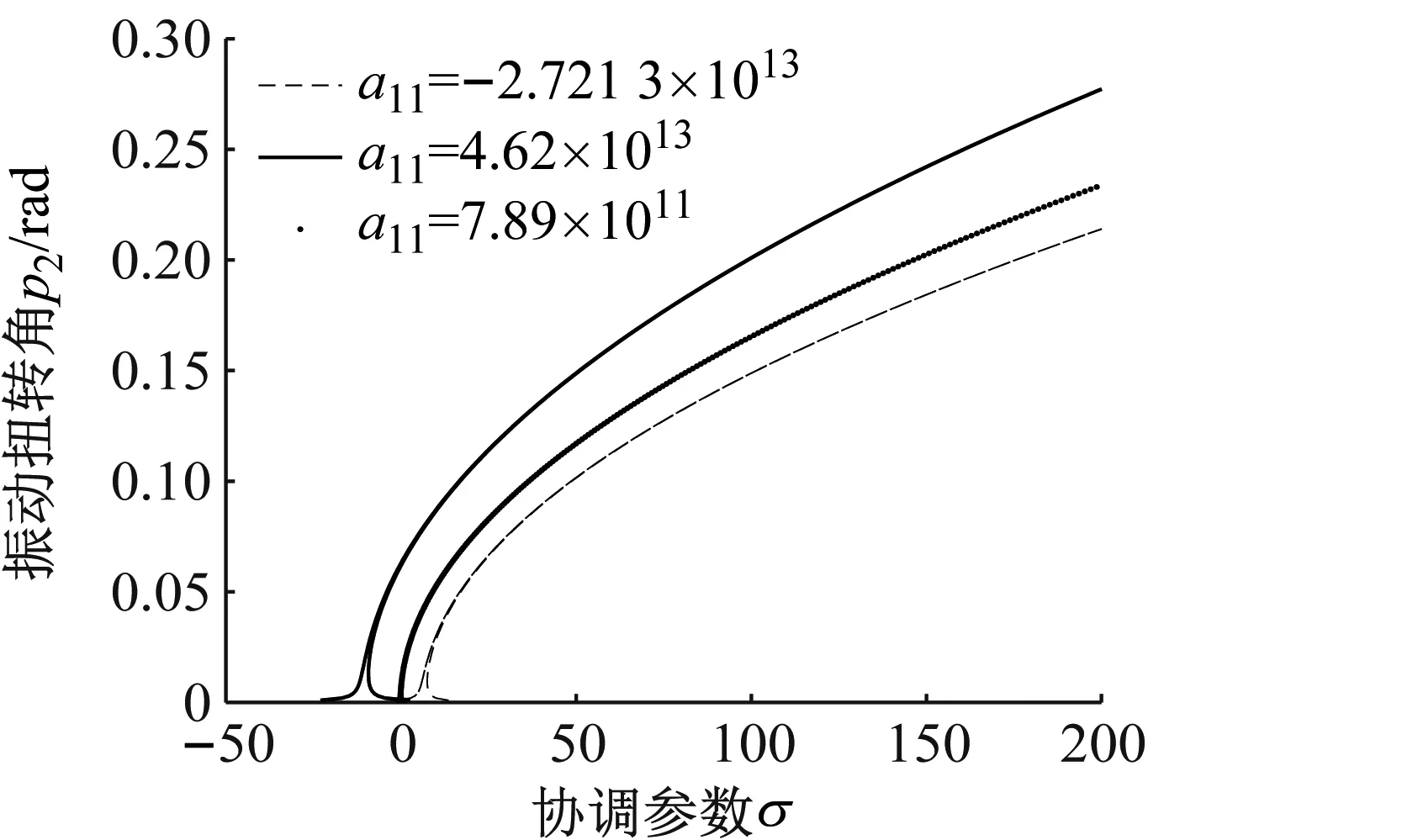
(b) 扭转方向图7 a11变化时垂直和扭转方向主共振幅频曲线Fig.7 The curve of primary resonance amplitude-frequency in vertical and torsional directions with different a11

由图7(a)可知，动态轧制力系数a11变化会引起轧辊在垂直方向的幅频曲线出现跳跃。由图7(b)可知，通过对比扭转方向的幅频曲线a11数值可看出a11为负时，轧辊的振动扭转角偏小；a11为正时，a11值越小系统振动扭转角越小。

当轧机倾角α一定，扭转方向动态轧制力矩系数b0数值变化时，轧机垂直扭转方向的幅频特性曲线,如图8所示。

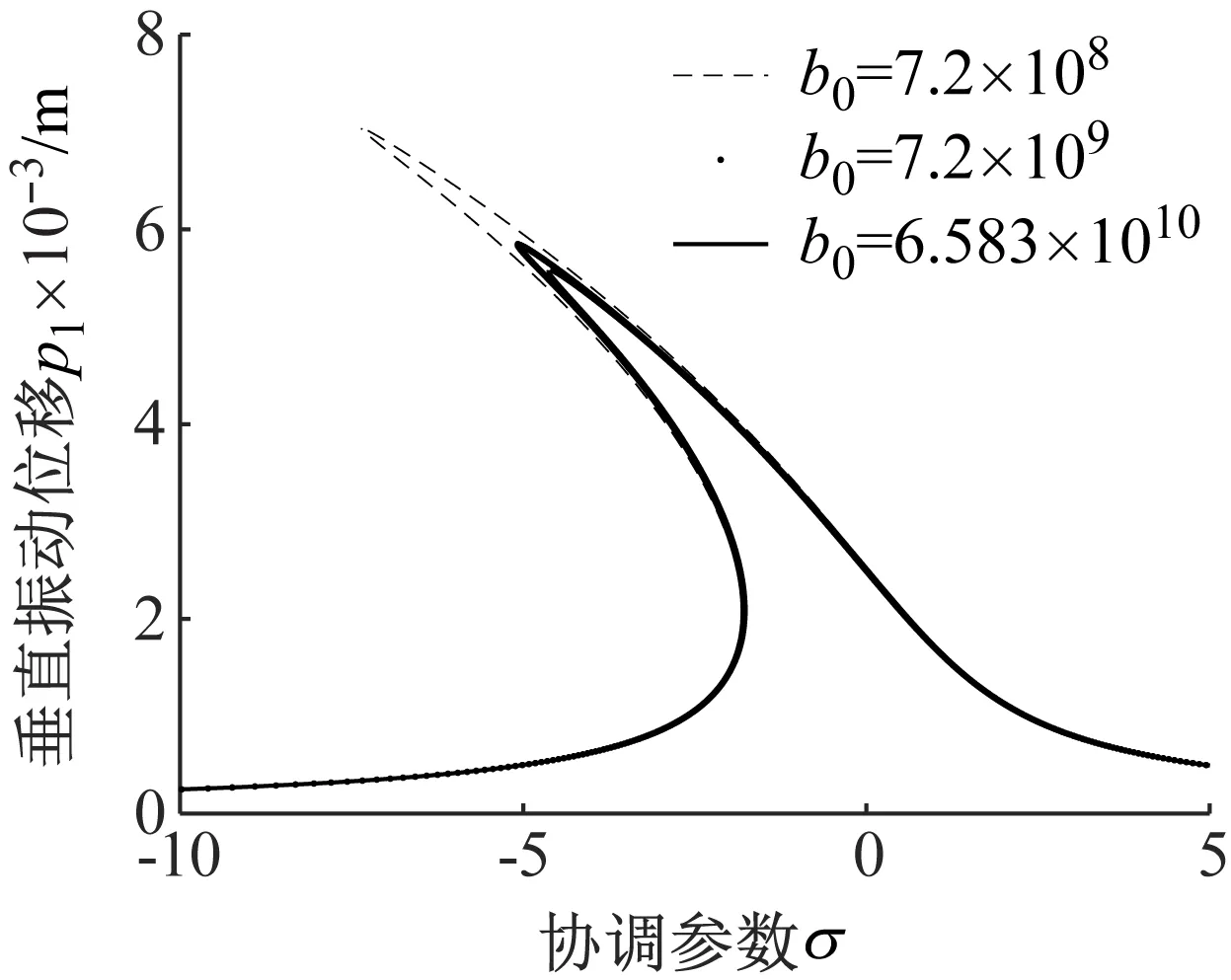
(a) 垂直方向

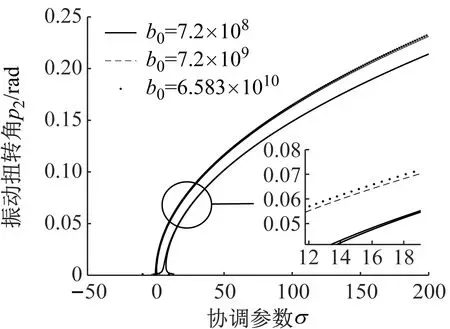
(b) 扭转方向图8 b0变化时垂直和扭转方向主共振幅频曲线Fig.8 The curve of primary resonance amplitude-frequency in vertical and torsional directions with different b0

由图8(a)可知，随着b0值增大，轧机垂直方向幅频曲线的幅值将会减小。由图8(b)可知，随着b0增大，轧机扭转方向两条永不相交的幅频曲线间距不断缩小。

当轧机接轴倾角α一定，接轴扭转刚度分别为0.3K,0.6K,K时，轧机垂直扭转方向的幅频特性曲线,如图9所示。

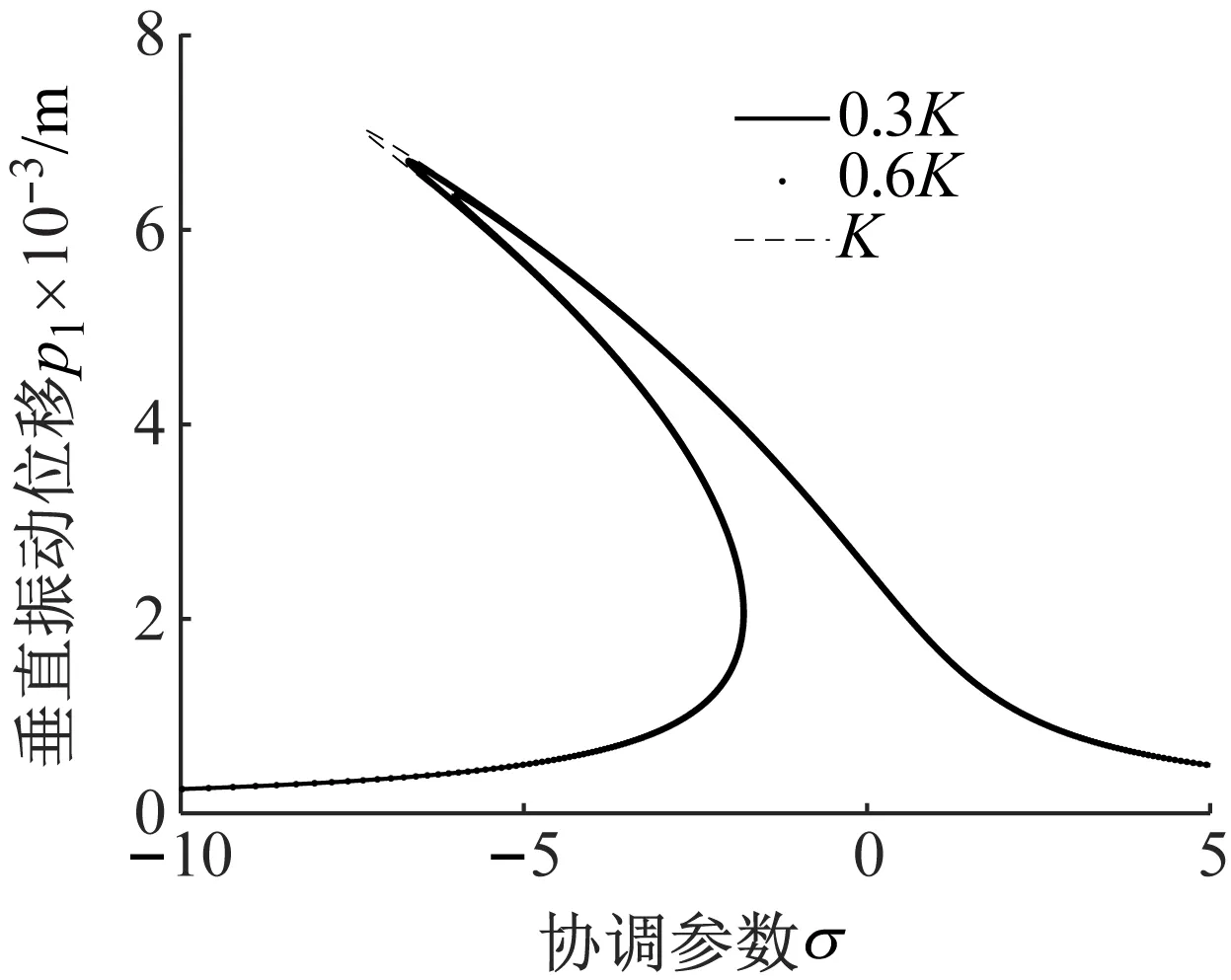
(a) 垂直方向

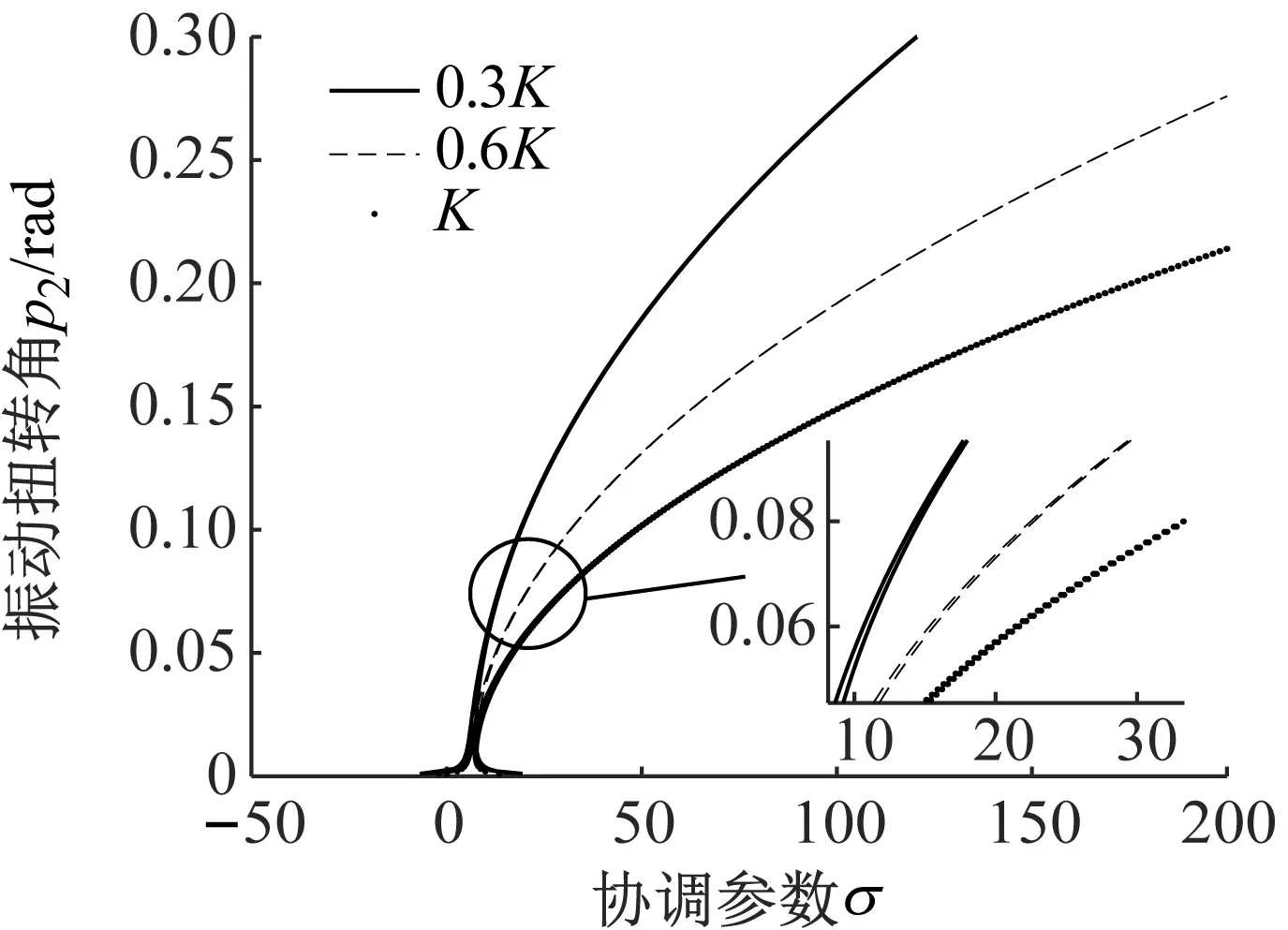
(b) 扭转方向图9 K变化时垂直和扭转方向主共振幅频曲线Fig.9 The curve of primary resonance amplitude-frequency in vertical and torsional directions with different K

由图9(a)可知,接轴扭转刚度减小，系统垂直方向幅频曲线的幅值将会减小。由图9(b)可知，扭转刚度从0.3K～K变化时，幅频曲线宽度变窄，且曲线右移，使得系统由软式非线性系统向硬式非线性系统发生转变。

轧机接轴倾角α一定时，外扰力幅值F0变化时，轧机垂直扭转方向的幅频特性曲线，如图10所示。

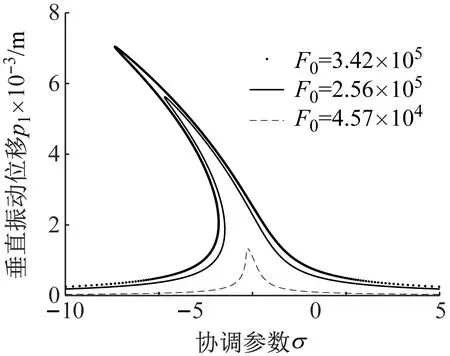
(a) 垂直方向

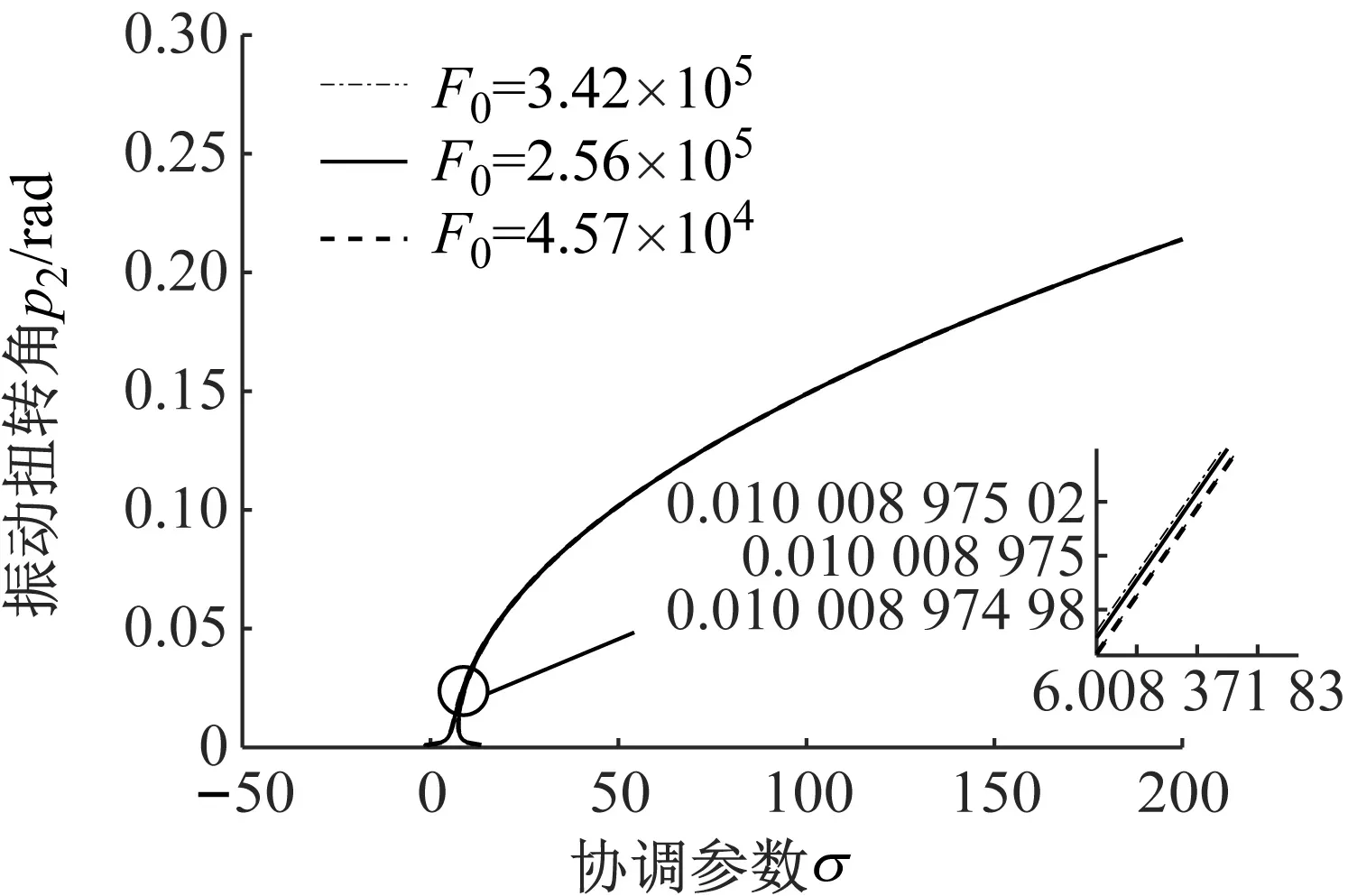
(b) 扭转方向图10 F0变化时垂直和扭转方向主共振幅频曲线Fig.10 The curve of primary resonance amplitude-frequency in vertical and torsional directions with different F0

由图10(a)可知，随着外扰力幅值F0减小，轧机垂直方向主共振幅频曲线幅值减小，且幅频曲线跳跃现象愈发不明显。由图10(b)可知，外扰力幅值变化对系统扭转方向的幅频曲线幅值影响不大，三条曲线几乎重合，但放大后仍可看出扭转方向幅频曲线幅值随外扰力幅值F0降低而减小。

6 结 论

(1) 考虑轧机主传动系统万向接轴倾角产生的附加动态弯矩影响，建立了板带轧机垂直—扭转非线性耦合振动模型。并利用多尺度法求解该耦合振动系统的幅频特性方程。

(2) 采用奇异性理论分析了板带轧机在不同因素影响下的转迁集及在转迁集不同区域的分岔结构。当分岔临界点的两侧解的数目变化越大，轧机垂扭耦合系统振动越剧烈，因此实际轧制生产中可调节d1、d2、d3的参数，避开临界点。

(3) 采用仿真发现轧机主传动系统接轴倾角α由2°增大到8°时，将会导致轧机垂直方向和扭转方向振动变强；而扭转方向动态轧制力矩参数b0增大和扭转刚度K增大，可以降低轧机的垂直方向和扭转方向的振动强度。此外垂直方向动态轧制力参数a11扰动力幅值F0变化均会影响轧机耦合振动的动力学行为，这为实际生产中轧机振动的控制和抑制提供了理论依据。