Static and dynamic stability responses of multilayer functionally graded carbon nanotubes reinforced composite nanoplates via quasi 3D nonlocal strain gradient theory

Ahmed Amine Dikh ,Mohmed Sid Ahmed Houri ,Mohmed Ouejdi Belri ,Slw A.Mohmed ,Mohmed A.Elther

a Laboratoire D＆apos;Etude des Structures et de M′ecanique des Mat′eriaux,D′epartement de G′enie Civil,Facult′e des Sciences et de La Technologie,Universit′e Mustapha Stambouli B.P.305,R.P.,29000,Mascara,Algeria

b Laboratoire de G′enie Energ′etique et Mat′eriaux,LGEM,Universit′e de Biskra,B.P.145,R.P,07000,Biskra,Algeria

c Department of Engineering Mathematics,Zagazig University,P.O.Box 44519,Zagazig,Egypt

d Faculty of Engineering,Mechanical Engineering Department,King Abdulaziz University,P.O.Box 80204,Jeddah,Saudi Arabia

e Faculty of Engineering,Mechanical Design and Production Department,Zagazig University,P.O.Box 44519,Zagazig,Egypt

Keywords:3D shear deformation theory Free vibration Buckling Bending Galerkin method Functionally graded nanotube Nonlocal strain gradient theory

ABSTRACT This manuscript presents the comprehensive study of thickness stretching effects on the free vibration,static stability and bending of multilayer functionally graded (FG) carbon nanotubes reinforced composite (CNTRC) nanoplates.The nanoscale and microstructure influences are considered through a modified nonlocal strain gradient continuum model.Based on power-law functions,four different patterns of CNTs distribution are considered in this analysis,a uniform distribution UD,FG-V CNTRC,FG-X CNTRC,and FG-O CNTRC.A 3D kinematic shear deformation theory is proposed to include the stretching influence,which is neglected in classical theories.Hamilton＆apos;s principle is applied to derive the governing equations of motion and associated boundary conditions.Analytical solutions are developed based on Galerkin method to solve the governing equilibrium equations based on the generalized higher-order shear deformation theory and the nonlocal strain gradient theory and get the static bending,buckling loads,and natural frequencies of nanoplates.Verification with previous works is presented.A detailed parametric analysis is carried out to highlight the impact of thickness stretching,length scale parameter(nonlocal),material scale parameter(gradient),CNTs distribution pattern,geometry of the plate,various boundary conditions and the total number of layers on the stresses,deformation,critical buckling loads and vibration frequencies.Many new results are also reported in the current study,which will serve as a benchmark for future research.

1.Introduction

Over the past two decades,Functionally Graded Materials(FGM)are revolutionary materials that solve the problem posed by laminated composite structures such as delamination,matrix-fiber debonding,matrix cracking,etc.[1].Due to outstanding properties such as high strength-to-weight and stiffness-to-weight ratios,good thermal and acoustic insulation as well as flexibility in design,the FGM are extensively used in modern industrial applications such as aircraft,energy and sensors,spacecraft,marine industry,medical field and civil engineering.The FGMs are a new advanced class of materials in which the mechanical properties vary smoothly and continuously from one surface to the other [2-6].Usually,the FGMs are made from a mixture of ceramic and metal in which,the ceramic materials have good thermal resistance as well as anti-oxidant behaviour and metallic materials have excellent strength and superior fracture toughness [7].

In recent years,Carbon Nanotubes (CNTs) are considered as“new materials for the twenty-first century” [8,9] instead of other nano-fillers due to their perfect bonding with the polymeric matrix and excellent properties in order to improve the mechanical,electrical,and thermal properties of composite structures [10,11].Exceptional mechanical properties of FGM and CNTs may be obtained together through functionally graded distribution of CNTs[12-18].Carbon nanotubes can offer extraordinary electrical conductivity,while others are semiconductors [19].They also have excellent thermal conductivity and tensile strength[20,21]because of their nanostructure and strength of the bonds between carbon atoms.Moreover,The CNTs can be chemically modified[22].These properties are expected to be valuable in various fields of technology,such as composite materials by replacing or complementing carbon fibers,nanoelectronics,optics,biotechnology,nanotechnology,and other applications of materials science.This propre combination of CNTs and FGM concept was first introduced by Shen [13] in his study on the nonlinear bending behaviour of functionally graded carbon nanotube-reinforced composites (FGCNTRC) plates.A detailed review of the recent progress of the FGCNTRC structures and their properties and applications are available in Refs.[14,23].

Due to the vigorous development in nanotechnology,the engineering nanostructures such as nanorods,nanobeams and nanoplates have been growing in numerous modern engineering industries [24-31].Since the structural behaviour in smalldimensions,i.e.,nano and micro,differ from the macro one.Also,due to extensive applications of small-scale structures and instruments in different areas of sciences such as measuring equipment [32],medicine [33],energy storage devices [34],and other industries [35],many researchers were interested in studying and analysing in small dimensions.In these applications,size effects become very prominent.Therefore,the inclusion of the size effects in the analysis of the mechanical behaviour of these nanostructures is very necessary for better designing or understanding these small-scaled structures.It should be noted that classical continuum mechanics theory does not suitable for nanostructures due to neglecting size influence in nanosize structures.To overcome this problem,various non-classical continuum theories imply additional material length scale parameters were developed,such as nonlocal elasticity theory proposed via Eringen [36-38],strain gradient theory (SGT) [39,40],modified couple stress theory(MCST) [41-45],surface elasticity theory [46] and nonlocal strain gradient theory (NSGT) [47,48].However,the studies of sizedependence effects on the mechanical behaviour of FG elastic materials with micro/nano-structure should be related to both internal lengths and external dimensions and are always of fundamental significance.In contrast to classical elasticity theory,the stress of nonlocal elasticity theory at a reference point accounts for not only the strain at the reference point,but also the strains at all points in the whole body [37].

With the increasing application of FGM nanostructures,understanding their responses becomes an important task.In the literature,three main theories have been proposed to analyse accurately the behaviour of FGM nanostructures.The classical plate theory (CPT),based on Kirchhoff＆apos;s assumptions,ignores the transverse shear strain and is suitable only to study thin plates/shells[49-51].However,it is not appropriate for the moderately thick and thick plates,which require that the transverse and normal strain should be taken into account.The next class of theory,known as first-order shear deformation theory (FSDT) which considers constant transverse shear stresses through the plate thickness[52-54].

However,it needs a shear correction factor whose value depends on several factors such as end condition,thickness scheme,material properties,etc.[55-57].To overcome the drawbacks of CPT and FSDT,various higher-order shear deformation theories(HSDT) were developed for a better representation of transverse shear stresses without the use of correction factors [58-71].

It is termed the sinusoidal shear deformation theory (SSDT),exponential shear deformation theory (ESDT),third-order shear deformation theory (TSDT),hyperbolic shear deformation theory(HHSDT) and so on.These theories include higher-order terms in the approximation of the in-plane displacement fields and satisfy zero shear stress conditions at the top and bottom surfaces of plates.

Based on the above-mentioned theories,many computational models,both analytically and numerically,have been proposed to investigate the linear and nonlinear static,buckling and vibration responses of FGM micro/nano-structures.Farajpour et al.[72]proposed a new size-dependent plate model based on higher order nonlocal strain gradient theory to examine the buckling response of orthotropic nanoplates under biaxial compression in thermal environment.Later,analysis of free vibration and buckling responses of simply supported FGM nanoplates in thermal environment is performed by Sobhy and Radwan[73]using a new quasi-3D nonlocal hyperbolic plate theory.Eringen＆apos;s nonlocal theory was used to capture the effect of the nonlocal parameter.Barati [74]carried out a dynamic analysis of porous FGM nanoplates using a nonlocal stress-strain gradient theory.Sahmani et al.[75] presented a unified nonlocal strain gradient plate formulation for the nonlinear axial post-buckling analysis of FGM porous micro/nano plates reinforced with graphene platelets.Karami et al.[76]developed a three-dimensional (3D) elasticity solution in conjunction with NSGT is to examine the mechanical behaviour of anisotropic spherical nanoparticles.She and Yuan[48]carried out a nonlinear bending and vibration analysis of FGM porous tubes using NSGT.Arefi et al.[77] presented a nonlocal elasticity theory based on a two-variable SSDT to analyse the free vibration behaviour of FGM polymer composite nanoplates reinforced with graphene nanoplatelets (GNPs),resting on a Pasternak foundation.

Recently,Karami et al.[78] carried out an analysis for the force resonance response of three-directional functionally graded Kirchhoff nanoplates using bi-Helmholtz nonlocal strain gradient theory.Karami and Shahsavari [79] employed a refined nonlocal strain gradient model to study the thermal stability of FGM sandwich nanoplates integrated with piezoelectric layers.Based on quasi-3D sinusoidal shear deformation plate theory as well as NSGT,Jalaei and Thai [80] examined dynamic instability of viscoelastic porous FGM nanoplates under biaxially oscillating loading and longitudinal magnetic field.Based on the FSDT and NSGT,Arefi et al.[81] carried out a bending analysis of sandwich nanoplates including a porous core and two piezomagnetic face sheets.By using the NSGT,Sharifi et al.[82] presented an analytical solution based on Navier＆apos;s method to determine the natural frequencies of FGM piezoelectric nanoplates.Thai et al.[83] studied the free vibration behaviour of multilayer functionally graded graphene platelet-reinforced composite (FG-GPLRC) microplates using the MSGT and HSDT.By employing the HSDT,Gao et al.[84] investigated analytically the nonlinear vibration of different types of functionally graded nanostructures using the NSGT.

More recently,based on the nonlocal elasticity model framework of classical Kirchhoff thin plate,Tahouneh et al.[85]examined the vibration response of a single-layered graphene sheet with corner cutout by employing the isogeometric analysis (IGA).They have[86] used the same method to analyse the impact of vacancy defects on the vibration of graphene sheets.

Fig.1.Geometry and cross-sections of FG-CNTRC laminated nanoplate.

Daikh et al.[87] presented a new quasi 3D hyperbolic shear theory in conjoint with NSGT to study the bending response of sigmoid functionally graded sandwich nanoplates rested on variable Winkler elastic foundation.Based on the HSDT,Thai et al.[88]proposed a novel nonlocal strain gradient model using the NSGT and isogeometric analysis to investigate the free vibration and bending responses of FGM plates.The Mori-Tanaka scheme was used to homogenize material properties.Later,based on the FSDT,Esmaeilzadeh et al.[89]employed the NSGT to study the nonlinear dynamic behaviour of bi-directional FGM porous nanoplates resting on elastic foundations.Tahouneh et al.[90]investigated the effects of temperature,site and size of vacancy defects on the mechanical properties of graphene using the Lekhnitskii interaction coefficients and Molecular Dynamic approach.

Shen et al.[100] studied the effect of both nonlocal scale and material length scale on the vibration and stability behaviours of FGM nanoplates with axial motion using the NSGT.Fenjan et al.[101]studied the effect of nonlocal and strain gradient parameters on the mechanical-hygro-thermal vibrations behaviour of FGM porous nanoplates using the differential quadrature method(DQM)and NSGT.Amir et al.[102] utilized the quasi-3D tangential shear deformation theory in conjunction with modified couple stress theory to analyse the free vibration response of a three-layered FG porous micro plate which is located between two polymeric nanocomposite layers.Sofiyev and Kuruoglu[103]studied the influences of combined loading and two-parameter elastic foundation on buckling behaviour of composite conical shells reinforced by CNTs.Arshid et al.[104] examined the porosity and the hygrothermal effect on the vibration behaviour of FGM plates embedded by piezoelectric nanocomposite face sheets stiffened by CNTs.

Based on the aforementioned review,it appears that the literature on the analysis of FGM nano structures is plenty.Unfortunately,there are limited works available in the literature for the bending,vibration and buckling analysis of FGM nano structures with CNT reinforcement.On the basis of the TSDT,Ravari and Zeighampour[105] investigated a vibration response of FG-CNTRC nanoplates using Mindlin＆apos;s strain gradient theory.By using the FSDT,Duc et al.[11] presented an analytical solution based on Navier＆apos;s technique to study the static and free vibration responses of FG-CNTRC rectangular plates resting on Winkler-Pasternak elastic foundations.By employing the isogeometric analysis (IGA),Phung-Van et al.[106]carried out a size-dependent analysis of FGCNTRC based on the generalized higher-order shear deformation theory (GHSDT).Similarly,Thanh et al.[107] examined static and free vibration behaviours of FG-CNTRC nanoplates using a new size-dependent model based on MCST and IGA.Di Sciuva and Sorrenti [108] studied the bending,free vibration and buckling of functionally graded carbon nanotube-reinforced (FG-CNTR) sandwich plates using a refined zigzag theory in conjunction with the Ritz method.Daikh et al.[109] proposed a new hyperbolic shear deformation beam theory to examine the static behaviour of simply supported multilayer nonlocal strain gradient nanobeam reinforced by CNTs under various loading profiles.They have also used the same methodology solution to study the size effect of nanoscale on free vibration and buckling of multilayered CNTRC and FG nanoplates in thermal environment by using the NSGT [110,111].Based on the quasi-3D hyperbolic shear deformation theory with NSGT,Shahraki et al.[112] carried out a buckling and vibration analysis of FG-CNTRC rectangular thick nanoplates resting on an elastic foundation with different boundary conditions using the generalized differential quadrature method (GDQM).Thai et al.[113] investigated numerically the bending and free vibration analyses of FG-CNTRC nanoplates using a moving Kriging meshfree model based on HSDT.Rasoolpoor et al.[114] investigated numerically the effect of CNTs on the low velocity impact of metallic nanocomposite plates.

As far as authors are aware,there is currently no publication available that explains the bending,vibration and buckling behaviours of FG-CNTRC nanoplates under various boundary conditions using an analytical solution based on quasi-3D nonlocal strain gradient theory.Therefore,the main purpose and the novelty of this paper is to propose a developed analytical solution based on Galerkin method to study bending,buckling and free vibration behaviour of FG-CNTRC plates by considering the thickness stretching effect using various boundary conditions.The volume fraction of CNTs is defined here based on a power-law function.Various parameters and factors are investigated in this paper.The accuracy of the proposed model is verified by comparing the obtained results with those available in the literature.The HSDT with stretching effect is utilized to examine in detail the influence of length scale parameter (nonlocal),material scale parameter(gradient),CNTs distribution pattern,geometry of the plate and the total number of layers on the bending,buckling and free vibration behaviour of FG-CNTRC plates using various boundary conditions.Matlab program is used to generate the algorithm,starting from including material properties and geometry of the plates until to obtain the stresses,deformations,critical buckling loads,and vibration frequencies.Referential results are presented for the first time which will serve as a benchmark for future studies in a similar direction.

2.Mathematical formulation

Consider a cross-ply multilayer plate of length,widthand thickness,as shown in Fig.1(a).Each layerof the CNTRC plate is made from a polymer matrix and reinforced by single-walled carbon nanotubes (SWCNTs),and all layers have the same thickness.The total number of layers is N (Fig.1(c)).

2.1.Material distribution functions

In the present study,as shown in Fig.1b,four different patterns of CNTs distribution are considered,the uniform distribution of CNTs along the nanoplate thickness(UD)and three FG distributions of CNTs (FG-X,FG-O and FG-V).

The volume fraction of CNTs ofth layer for various patterns,are expressed as follows [115].

FG-X CNTRC laminated nanoplate:

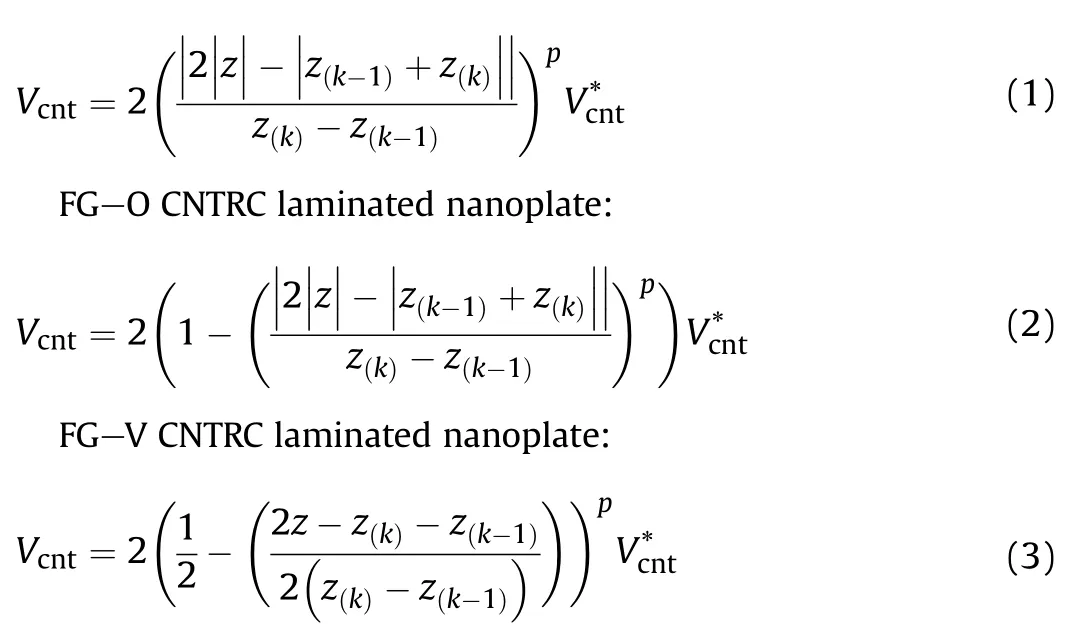
UD CNTRC laminated nanoplate:

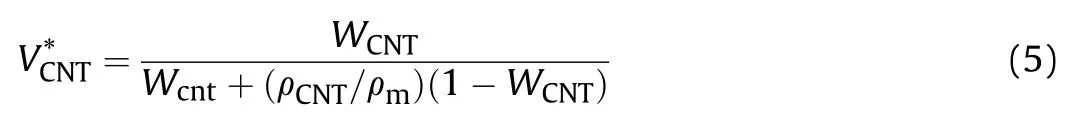
where,ρand ρare the CNTs mass fraction,CNTs mass density and polymer matrix mass density,respectively.

To define the effective Young＆apos;s modulus and shear modulus of the CNTRC nanoplates,the extended rule of the mixture and the molecular dynamics simulations given by Han and Elliott [116] is used

Poisson＆apos;s ratio νand mass density ρ oflayer are expressed as[117,118]:

In addition,the other effective mechanical properties of the mixture of CNTs and matrix isotropic polymer are given as

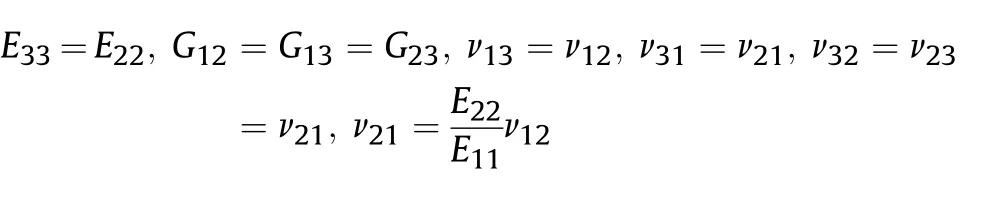
2.2.Nonlocal strain gradient theory

By the coupling physical impact of the strain gradient stress and nonlocal elastic stress fields,Lim et al.[119]proposed a function of stresses as:

Cis the elastic constant,andcapture the nonlocal effects andcaptures the strain gradient effects.α（,,）and α（,,）are the nonlocal kernel functions that satisfy the developed conditions by Eringen [36],The constitutive relation of nonlocal strain gradient theory can be expressed in the form

where ∇is the Laplacian operator.In this study,we assume the coefficient＝＝.The total nonlocal strain gradient constitutive relation takes this form

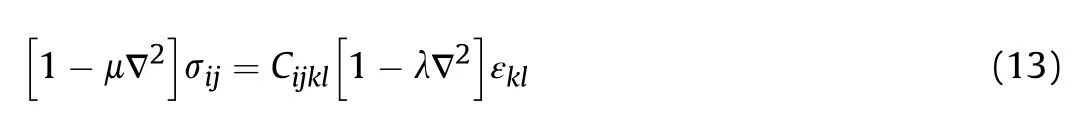
where μ ＝（）and λ ＝.

2.3.Displacement field

By considering the continuous variation of shear through the thickness and satisfies zero shear at the top and bottom surface,the displacement field of general point（,,）in the CNTRC plate can be written as [120]:

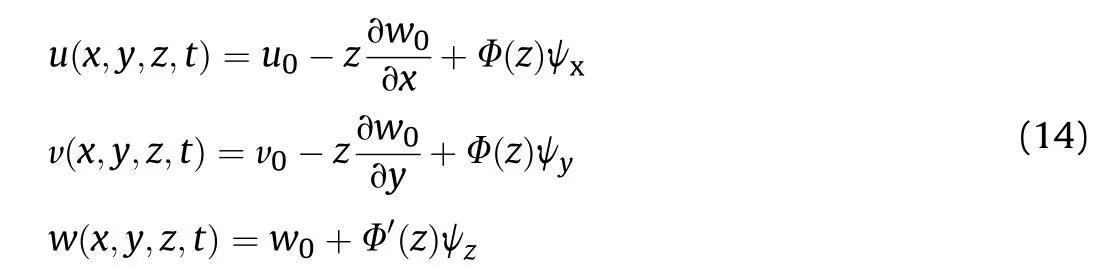
where (,v,) and (ψ,ψ) signified the displacements and rotations of transverse normals on the plane z ＝0,and ψis additional displacement to show the inclusion of normal deformation.

Based on the kinematic displacement field given in Eq.(14),the normal and shear strains at any generic point through the domain of the plate can be evaluated by

The constitutive stress-strain equations of nonlocal strain gradient nanoplate can be governed by

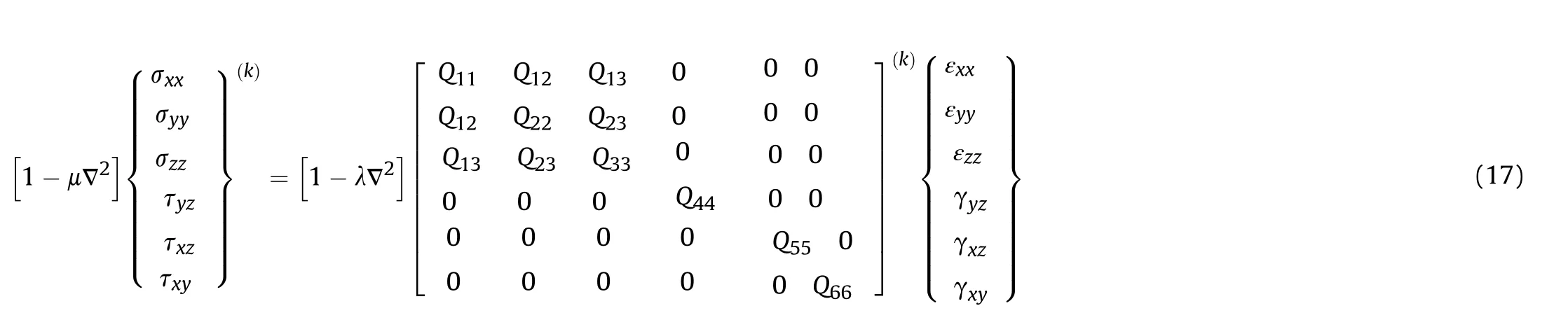
where

Since the CNTRC laminate is made ofth layers,the constitutive stress-strain relations are stated as:

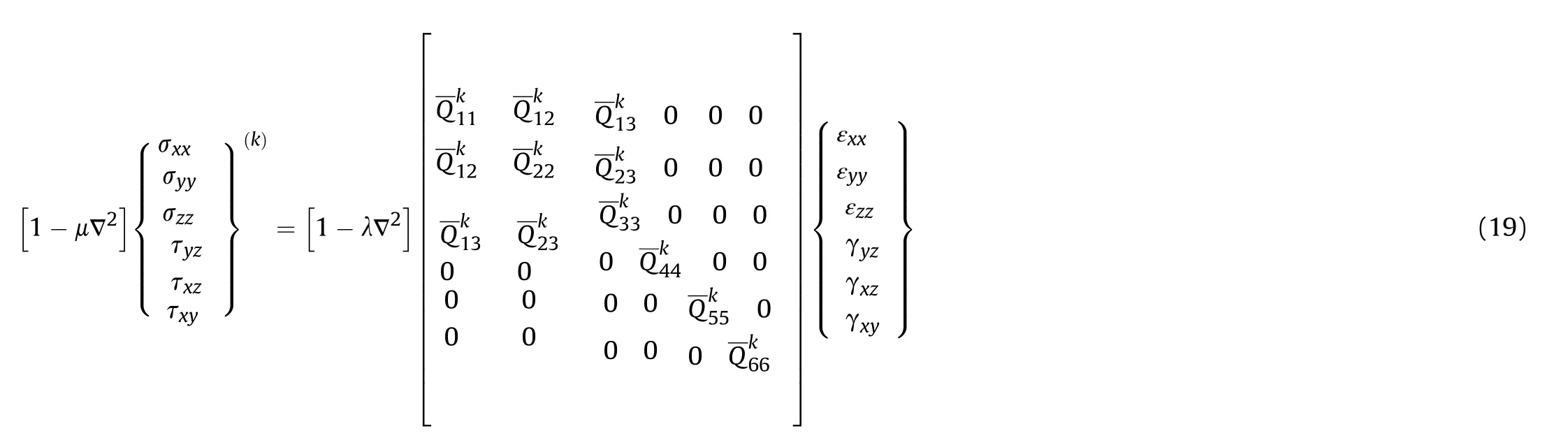
where θis the lamination angle of theth layer.

2.4.Variational statements

Hamilton＆apos;s principle is employed to formulate the equations of motion of the CNTRC nanoplate:

where,andare the strain energy,the kinetic energy and the virtual work done by the external forces,respectively.

Firstly,the expression of the virtual strain energy is:

Substituting the transverse displacement in the classical constitutive equation,and integration over the thickness direction,one obtains

The force and moment resultants can be portrayed by

In terms of vibration analysis of the plates,the virtual kinetic energy of the system can be expressed as follows:

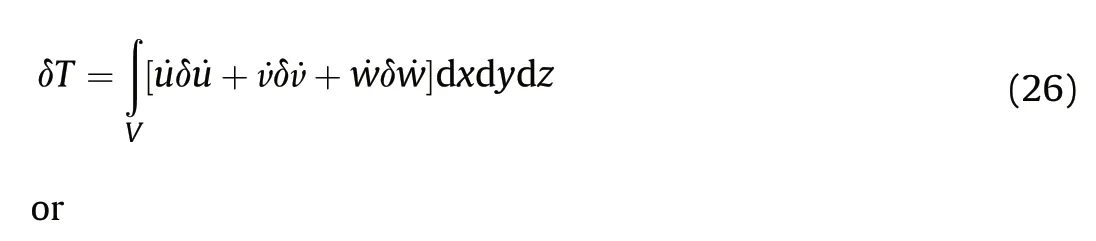
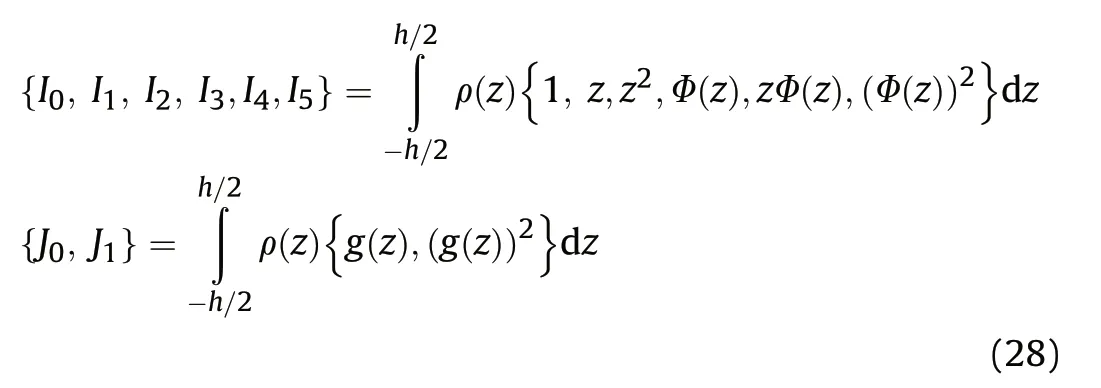
Therefore,the equilibrium equation can be presented by

To consider the length scale and microstructure effect of nanoplate,substitute Eq.(29) into nonlocal strain gradient constitutive equation described by Eq.(19),yields

Therefore,the governing equilibrium equation of CNTRC nonlocal strain gradient nanoplate can be described by

3.Analytical solution

The analytical solution of Eqs.(34)-(39) can be solved using Galerkin approach for rectangular plates under various boundary conditions.The expressions of generalized displacements can be expressed a:

Here, U, V, X, Zand Ψare arbitrary parameters.denotes the intensity of the load at the nanoplate center.m and n are mode numbers.The functions X（）and Y（）that satisfy the above boundary conditions are given in Table 1 as[123].where λ ＝π/,μ ＝π/.By substituting Eq.(39) in Eqs.(33-38),one obtains

Table 1 The admissible functions Xm（x）and Yn（y）.

Table 2 Dimensionless central deflections of simply supported single layer CNTRC square plates(a/h ＝10).

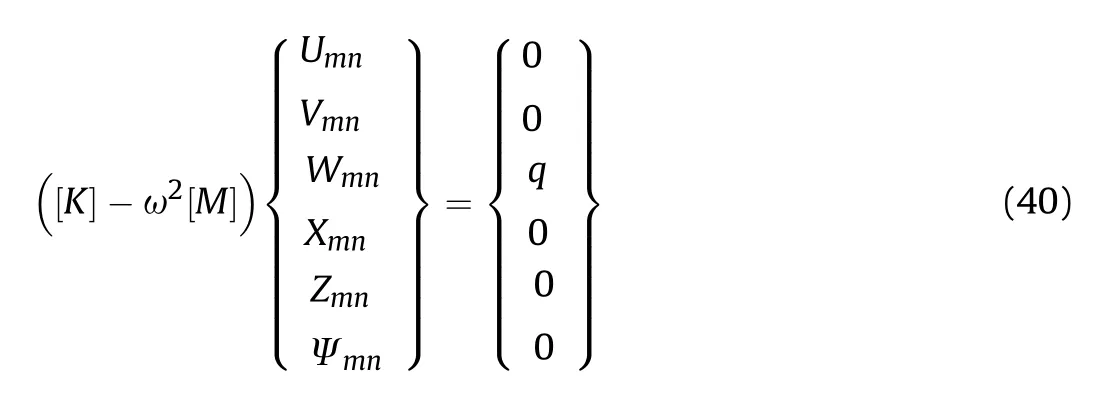
where [] et [] are the rigidity matrix and the mass matrix,respectively.

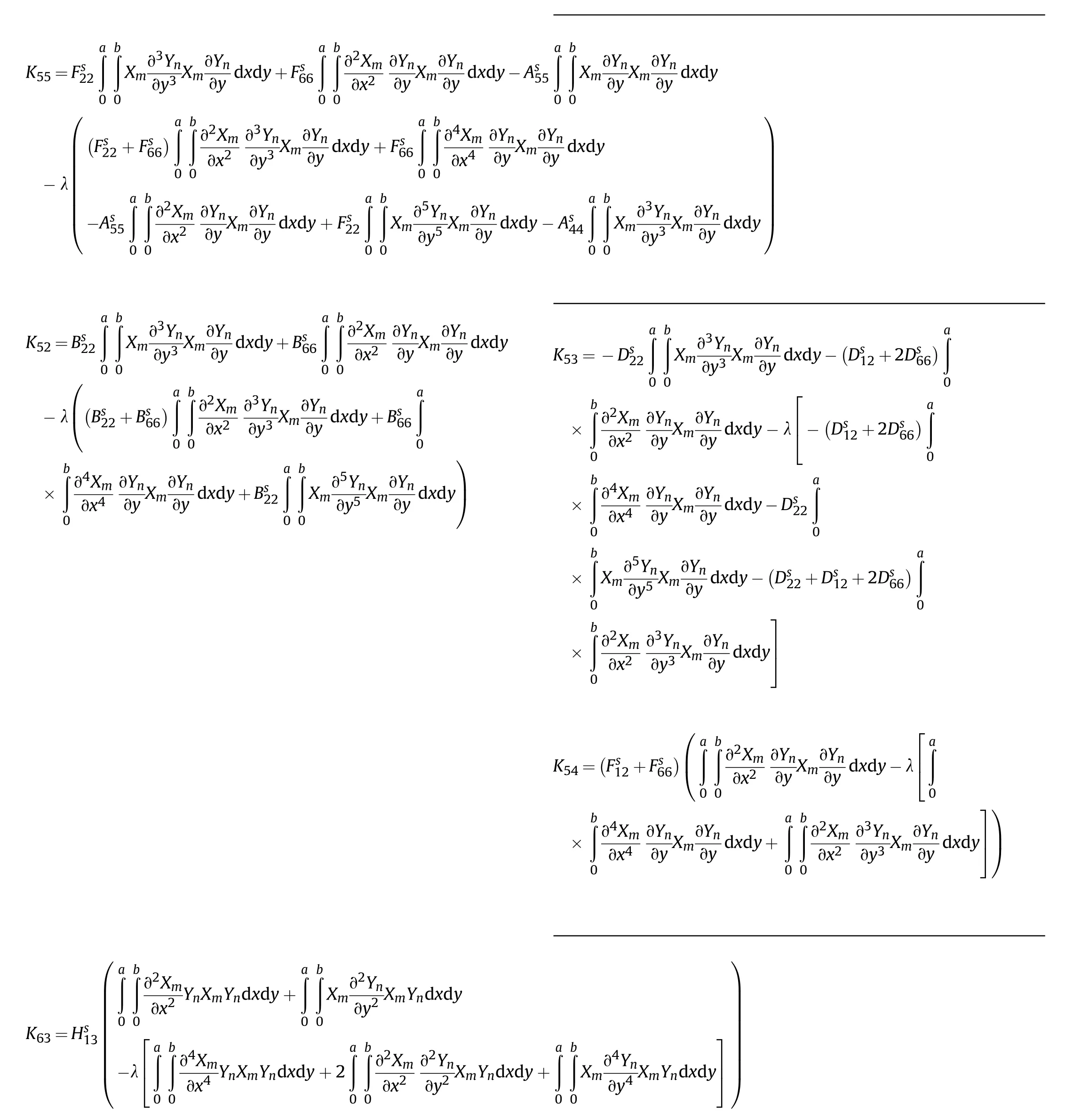
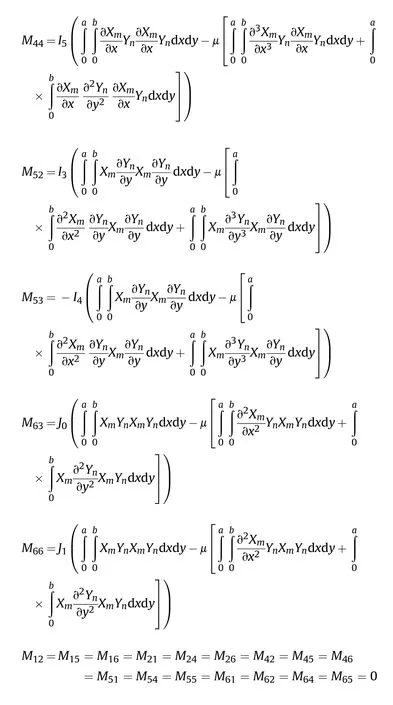
The elements Kand Mof the matrix [] and [] are given in Appendix A.

For the bending analysis,the sinusoidal applied load can be written as [124]:

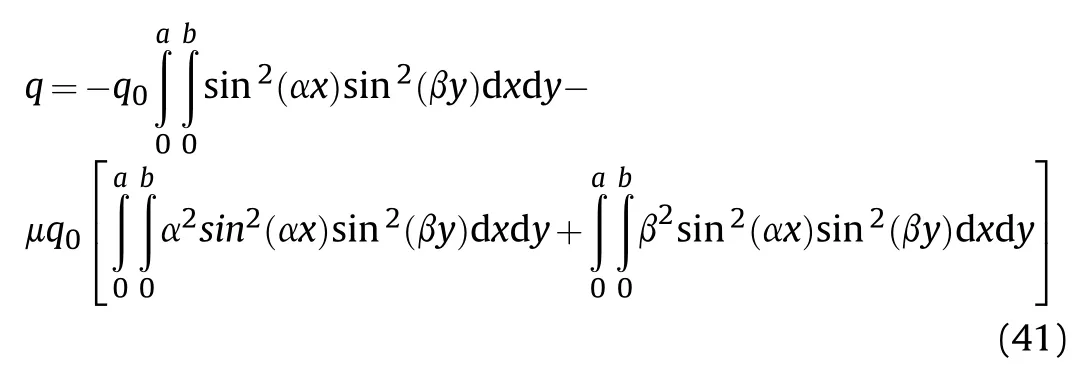
4.Numerical results

For simplicity,the normalized parameters for bending,buckling and vibration analyses of CNTRC plates are evaluated with the following forms:

Dimensionless displacements:

4.1.Verification and comparison

For the verification purpose,the performance of the proposed Quasi 3D analytical model is firstly carried out by comparing it with the analytical solution of Wattanasakulpong and Chaikittiratana[125] using TSDT and SSDT.In the present analysis,a simply supported single layer FG-CNTRC plate is considered.The computational results are obtained for various CNTs reinforcement distributions and CNTs volume fractions.The dimensionless central deflection results of FG-CNTRC plates (＝0) subjected to a transversely sinusoidal loading are highlighted in Table 2,while Tables 3 and 4 are for dimensionless critical buckling load and dimensionless frequency,respectively.It can be observed that the inclusion of the thickness stretching effect has a remarkable impact on the results.Also,it is seen that the plate with X distribution of CNTs has the strongest capacity to resist bending and buckling with the smallest deflection and highest critical buckling load.

Since the proposed quasi-3D theory and other quasi-3D theories include the thickness stretching effect,their solutions are very close to each other.However,the 2D solutions,which omits this effect,gives an inaccurate prediction.Also,it can be observed that the quasi-3D solutions,obtained lower critical buckling loads and frequencies,and higher displacement than the 2D solutions which eliminate the stretching effect.

a.Deflection and stresses

Table 3 Dimensionless critical buckling loads of simply supported single layer CNTRC square plates(a/h ＝10).

Table 4 Dimensionless frequencies of simply supported single layer CNTRC square plates(a/h ＝10).

Table 5 Various dimensionless displacements and stresses of simply supported FG-CNTRC square plates(a/h ＝10, ＝0.17).

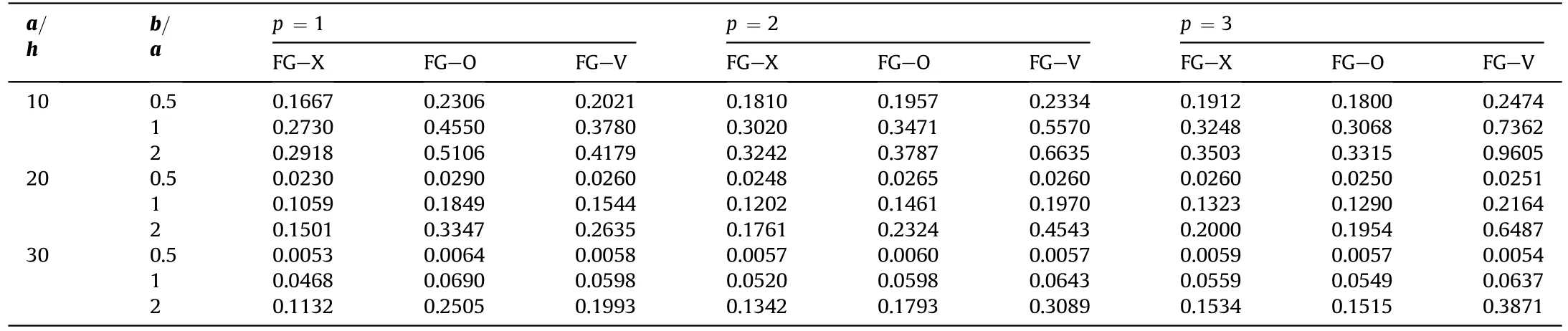
Table 6 Dimensionless central deflection under effect of the plate geometry(p ＝1,N ＝1,SSSS,V*CNT ＝0.17).

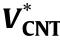
Table 7 Effect of boundary conditions on dimensionless deflection of CNTRC laminated square plates(p ＝1,a/h ＝10, ＝0.17).

In Fig.3,we investigated the influence of the number of layers on the central deflection of cross-ply FG CNTRC laminated plates for various power-law indexand various distribution types.The FG CNTRC plates with two layers (0/90) have the highest deflection wherever the distribution type is.The increase in the total number of layers improves the flexural stiffness of the plate and therefore decreases the central deflection.For the case of FG-X and FG-X plates,it is observed that the augmentation of power-law indexdecreases the values of central deflections by improving the stiffness of the plate.

Further,it can be observed that the plates with FG-X distribution have the highest stiffness and the smallest transverse displacement rather than other distributions,and,the FG-V distribution has the softest stiffness and highest deflection.The increase in power-law index(see Fig.2) lead to an increment of the total volume fraction of CNTs for the case of FG-O distribution,and lead to a decrement of CNTs for the case of FG-X and FG-V distributions.Therefore,from Fig.3,it is observed clearly that the increase of the indexincreases the FG-O plate stiffness and reduces the FG-X and F-GV plate stiffness.

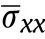
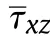
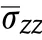
Fig.2.Variation of CNTs volume fraction along the thickness of the CNTRC plate;(a): X distribution,(b): O distribution,(c): V distribution.

Fig.3.Effect of number of layers on central deflection.(a): X distribution,(b): O distribution,(c): V distribution (a/h ＝10,b/a ＝1).(SSSS,b/a ＝1,a/h ＝10, ＝ 0.17).

Fig.4.Dimensionless axial stress distribution through the SSSS plate thickness;(a): X distribution,(b): O distribution,(c): V distribution.(N ＝1, b/a ＝1, a/h ＝10, ＝ 0.17).

Fig.5.Dimensionless shear stress distribution through the SSSS plate thickness;(a):X distribution,(b):O distribution,(c):V distribution.(N ＝1,b/a ＝1,a/h ＝10,V*CNT ＝0.17).

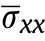
Fig.7 plots the different dimensionless transverse displacement of simply supported FG CNTRC plate by considering the CNTs distributions and the power-law index.The maximum values of displacement are for the FG-V plate with power-law index＝3.Whereas,the minimum values are observed for FG-X plate with index＝1.

The influence of aspect ratio/on the central deflection by considering various power-law index values is depicted in Fig.8.It is seen that the increase of the geometrical parameter/leads to an increment in central deflection.For aspect ratio/＞2,the deflections are almost constant regardless of the FG plate type and index.In the case of the X distribution and V distribution,the increase of the indexincreases the central deflection,however,the central deflection decreases by increasing the index.

In Fig.9,the impact of thickness ratio/on the central deflection for various boundary conditions is demonstrated.The central deflection decreases with the increase of the geometrical parameter/.In addition,it is clear that the maximum deflections are for the simply supported (SSSS) plates wherever the CNTs distribution type is,while the minimum values are for the CCSS plates.The results are almost constant regardless of the FG plate type and boundary conditions for thickness ratio/＞20.

b.Buckling response:

In this section,the influence of the plate geometry,the material characterization,axial compressive loads intensity and various boundary conditions on the dimensionless critical buckling load of FG CNTRC plates is presented.

Table 8 presents the effect of aspect ratio,thickness ratio,powerlaw index and various CNTs distributions on dimensionless critical buckling load of FG CNTRC plates subjected to a compressive uniaxial/biaxial in-plane loading.In Table 9,the impact of various boundary conditions and the number of layers is presented.The effect of the mentioned parameters is detailed in Figs.10-12.

In Fig.10,we demonstrate the effect of the number of layers N on the critical buckling loads of cross-ply FG CNTRC laminated plates for the three power-law indexand various distribution types.The highest critical buckling loads are for FG CNTRC plates with number of layers N ＝2 (0/90) wherever the distribution type is.The increase in the number of layers improves the plate stiffness and therefore increase the critical buckling loads.

Fig.6.Dimensionless transverse stress distribution through the SSSS plate thickness;(a): X distribution,(b): O distribution,(c): V distribution.(N ＝1, b/a ＝1, a/h ＝10 V*CNT ＝0.17).

Fig.7.Dimensionless transverse displacement through the thickness of simply supported FG CNTRC plate (N ＝1, b/a ＝1, a/h ＝10, ＝0.17).

The effect of thickness ratio/and power-law indexon critical buckling load of simply supported FG CNTRC plates is plotted in Fig.11.We can observe that the increase of the ratio/leads to increment of critical buckling loads where the smallest values of buckling loads occur in the case of biaxial compressive loads (χ＝χ＝1).

Using various boundary conditions,the influence of the aspect ratio/and the intensity of the in-plane compressive load χis plotted in Fig.12.The coefficient of the in-plane compressive load in x-direction is assumed constant (χ＝1),while the compressive loads in y-direction vary from 0 to 3.Except for the case of χ＝0,dimensionless critical buckling load increases as aspect ratio increases.Also,the intensity of in-plane loads has an important impact on critical buckling load,where increasing compressive inplane loads lead to a decrement of buckling loads.

c.Free vibration response:

In this section,we analyse the free vibration frequencies of FG CNTRC plates under the effect of various parameters.In Table 10,the dimensionless frequencies are tabulated for various boundary conditions,CNTs distribution types and various power-law indexes.To view more the influence of various factors,Figs.13-15 are presented.

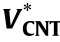
Table 8 Dimensionless critical buckling loads of simply supported FG CNTRC plates subjected to a compressive uniaxial/biaxial in-plane loading (N ＝1, ＝0.17).

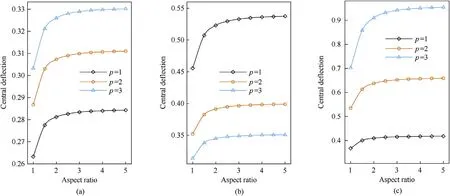
Fig.8.Dimensionless central deflection versus the aspect ratio;(a): X distribution,(b): O distribution,(c): V distribution.(SSSS,N ＝1, a/h ＝10, ＝0.17).

Fig.9.Dimensionless central deflection versus the Thickness ratio;(a): X distribution,(b): O distribution,(c): V distribution.(p ＝1,N ＝1,b/a ＝1, ＝0.17).

The effect of thickness ratio (/) on the frequency of CNTRC plates is plotted in Fig.13.It is clear that the frequencies decrease by increasing of/ratio.Similar results are obtained for various power-law indexes,especially for the FG-X plate.Fig.14 plots the effect of the aspect ratio.The dimensionless frequencies decrease with the increase of aspect ratio and the results are almost constant for ratio/＞2.

In Fig.15,dimensionless frequencies of FG-X CNTRC plates versus the vibration modes m and n are investigated using various boundary conditions.The modes m and n are varied from 1 to 5.It can be seen that the frequencies increase by increasing the vibration mode,and the difference between results reduce when the modes m and n increase.

d.Size-scale effect:

In this step,we investigate the impact of nonlocal and length scale parameters on deflection,buckling and free vibration of FG CNTRC plates (Tables 11-13).It is apparent that the nonlocal and length scale parameters have an important effect on the plate stiffness and therefore the mechanical response of the plate.

Table 9 Effect of boundary conditions on critical buckling loads of FG CNTRC laminated square plates(a/h ＝10, ＝0.17).

Table 10 Dimensionless frequency of FG CNTRC square plates(N ＝1,a/h ＝10, ＝0.17).

Table 11 Effect of nonlocal and length scale parameters on dimensionless central deflection (b/a ＝1, a/h ＝10,N ＝1, ＝0.17).

Table 12 Effect of nonlocal and length scale parameters on dimensionless critical buckling loads (b/a ＝1,a/h ＝10,N ＝1,＝0.17).

Table 13 Effect of nonlocal and length scale parameters on dimensionless frequency (b/a ＝1, a/h ＝10,N ＝1, ＝0.17).

Fig.16 shows the variation of bending,buckling and vibration responses of simply supported FG-X CNTRC square plates with the nonlocal parameter μ,with (λ ＝0 nm).In this figure,the deflection,and frequency ratios are defined as the ratios of those predicted by the nonlocal results (μ≠0) to the correspondences predicted by the local result (μ ＝0).It can be seen that the deflection ratio is greater than unity,whereas the frequency ratios and buckling ratios are smaller than unity.It means that the local theory underestimates the deflections and overestimates the natural frequencies and the critical buckling load of the FG CNTRC plates compared to the nonlocal one.This is because the local theory is unable to capture the small-scale effect of the nanoplates.Also,this figure shows that the responses of critical buckling load vary nonlinearly with the nonlocal parameter.

Unlike the nonlocal parameter effect,by considering the lengthscale parameter λ,from Fig.17,it can be seen that the frequency and buckling ratios is greater than unity,whereas the deflection ratios are smaller than unity.

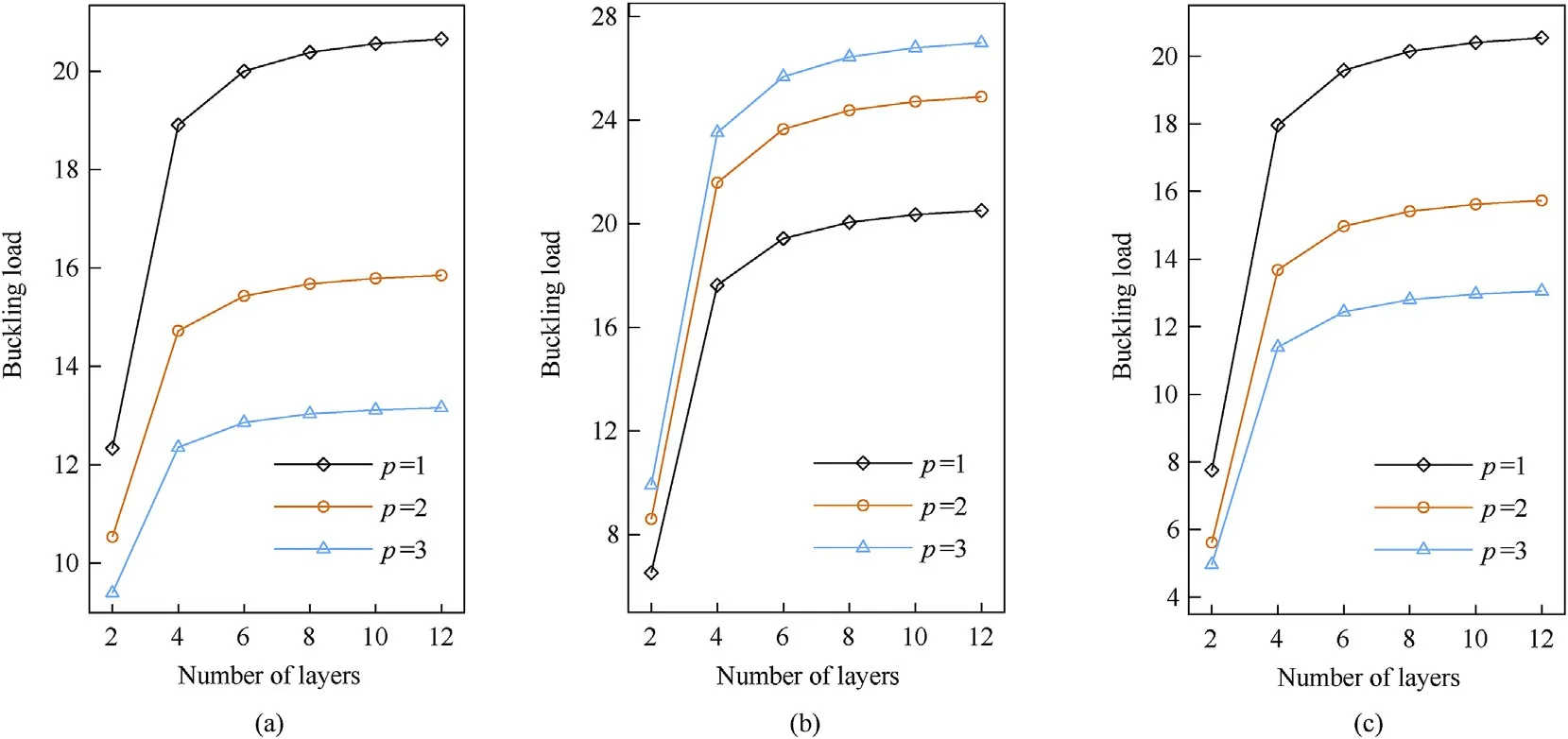
Fig.10.Effect of number of layers on buckling load;(a): X distribution,(b): O distribution,(c): V distribution.(SSSS, b/a ＝1, a/h ＝10, ＝0.17).

Fig.18 shows the influence of the nonlocal and length scale parameters μ and λ on the fundamental frequency ratios for four different boundary conditions.One can note that the fundamental frequency ratios are a monotonically decreasing function of μ,while λ is a monotonically increasing function,and the minimum values occur at the boundary condition CCSS while（λ ＝0）,and at the boundary condition SSSS for（μ ＝0）.

Fig.19 presents the variation of the frequency ratio against the nonlocal parameter and length scale parameters μ and λ for different values of thickness parameter (/) of simply supported square FG-X CNTRC plates.These results indicate that the responses vary nonlinearly with the small-scale parameters μ and λ.The main finding from the figures is that all responses of FG-X CNTRC nano-plate with lower thickness parameter(i.e.,/＝5)are strongly affected by the small-scale parameter μ and λ than those of the FG-X CNTRC nano-plate with relatively higher thickness parameters.From this observation,it can be concluded that modelling based on the local (classical) plate models is not suitable,and the nonlocal plate models may provide an adequate approximation for the nano-sized structures.

Fig.20 presents the variation of the frequency ratio against the nonlocal parameter and length scale parameters μ and λ for different values of aspect ratio (/) of a simply supported square FG-X CNTRC plates.The results show that increasing the aspect ratio,natural frequency ratio reduces for（μ ≠0,λ ＝0）and augments for（μ ＝0,λ ≠0）.This due to the reduction and augmentation of the stiffness of nanoplates with increasing the nonlocal and length scale parameters μ and λ respectively.For smaller aspect ratios of the nanoplates,the non-dimensional natural frequency parameters decrease linearly with nonlocal and length scale parameters.However,for higher aspect ratios of the nanoplates,the variation of the natural frequency ratio is smoother and follows a slightly nonlinear way with nonlocal and length scale parameters.

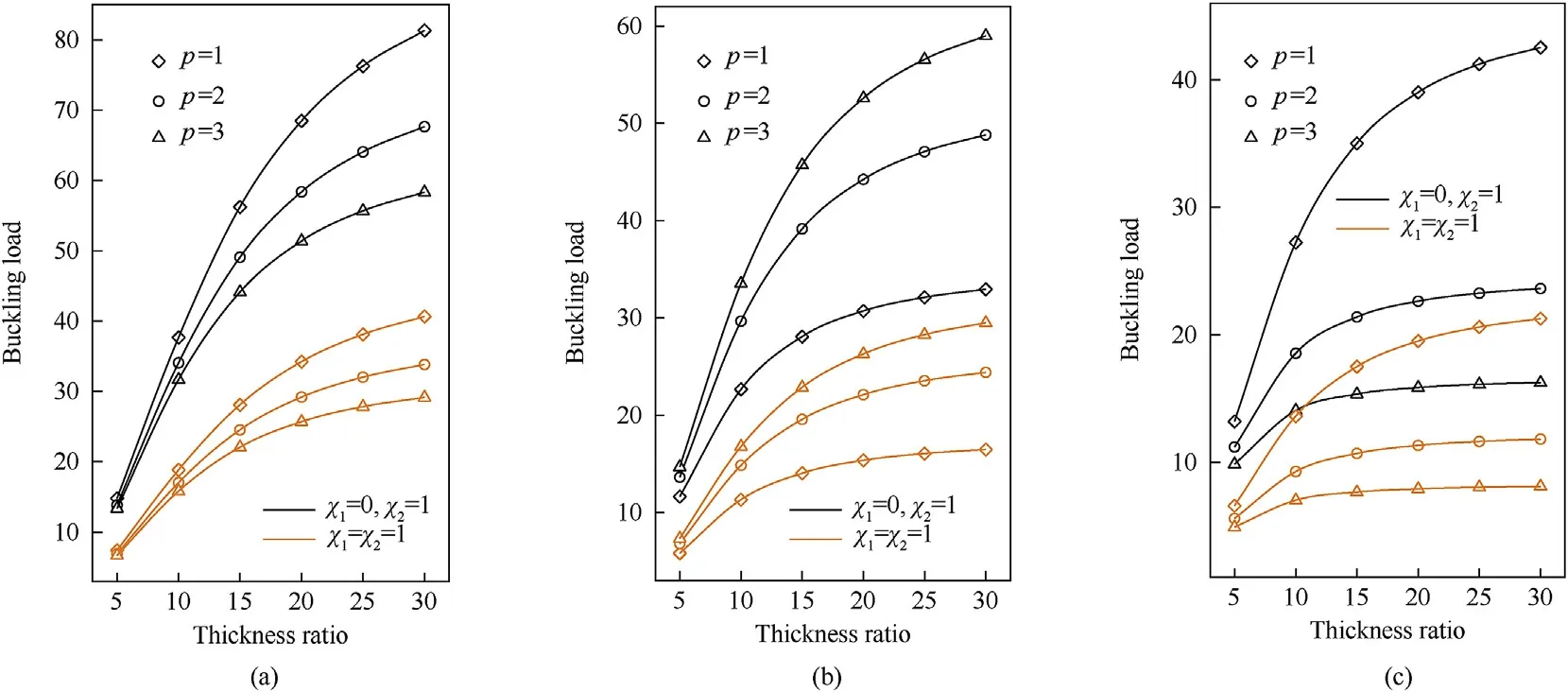
Fig.11.Dimensionless critical buckling load versus the thickness ratio;(a): X distribution,(b): O distribution,(c): V distribution.(SSSS,N ＝1, b/a ＝1, ＝ 0.17).

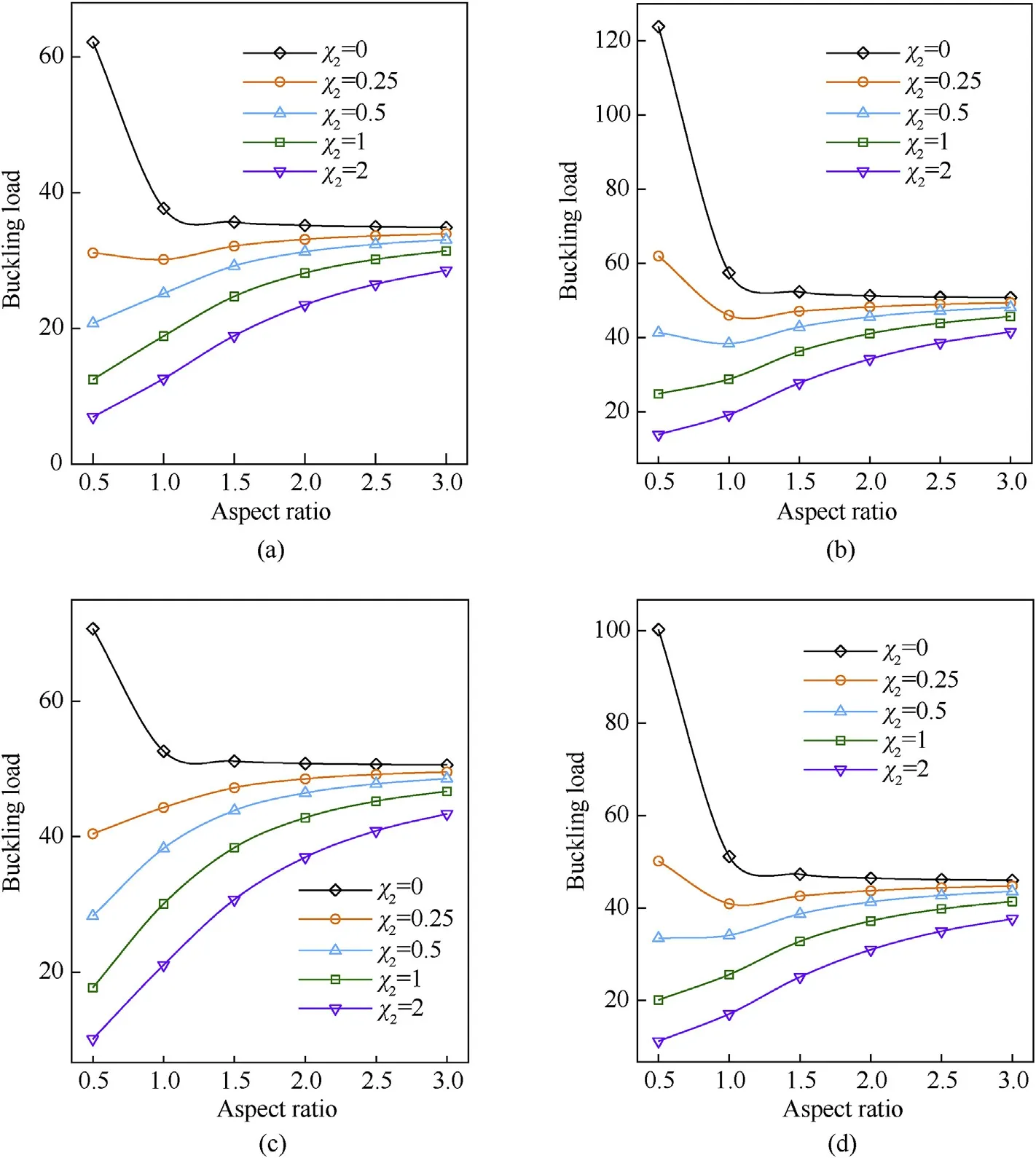
Fig.12.Dimensionless critical buckling load versus the aspect ratio;(a): SSSS,(b): CCCC,(c): CSCS,(d): CCSS.(p ＝1,FG-X,χ1 ＝1,N ＝1,a/h ＝10, ＝0.17).

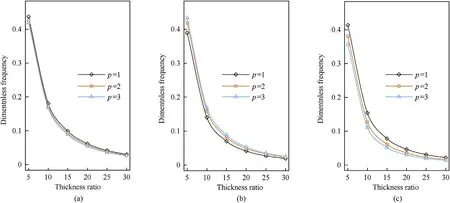
Fig.13.Dimensionless frequencies versus the thickness ratio;(a): X distribution,(b): O distribution,(c): V distribution.(SSSS,N ＝1, b/a ＝1, ＝0.17).

5.Conclusion

In the present work,comprehensive study of thickness stretching effects on the vibrational frequencies,deflection,stresses and static stability of single/multilayer functionally graded (FG)carbon nanotubes reinforced composite (CNTRC) nanoplates.Hamilton＆apos;s principle is employed to derive the governing.Analytical solutions are developed based on Galerkin method to solve the governing equilibrium equations based on the generalized higherorder shear deformation theory and the modified continuum nonlocal strain gradient theory.Three different patterns of CNTs distribution are considered in this analysis based on a power-law function.The performance and reliability of the proposed solutions by considering the stretching effect is validated by comparing it with the existing analytical solutions and parametric analysis is carried out to highlight the influence of thickness stretching,length scale and material scale parameters,CNTs distribution pattern,geometry of the plate,various boundary conditions and the total number of layers on the mechanical response of the proposed structure.The important key points that can be concluded from this investigation are summarized as follows:

· Increasing the number of layers can improve the stiffness of the CNTRC plates and have an excellent response for number of layers more than 4.

· The inclusion of thickness stretching has a significant effect on the response of the CNTRC plate.

· The inclusion of nonlocal parameter leads to a decrement of plate stiffness,therefore decrement in buckling loads and frequencies and an increment in transverse displacements,while the opposite is found when increasing length-scale parameter.

· The geometry and composition of the plate have an important effect on the response of the CNTRC plate.

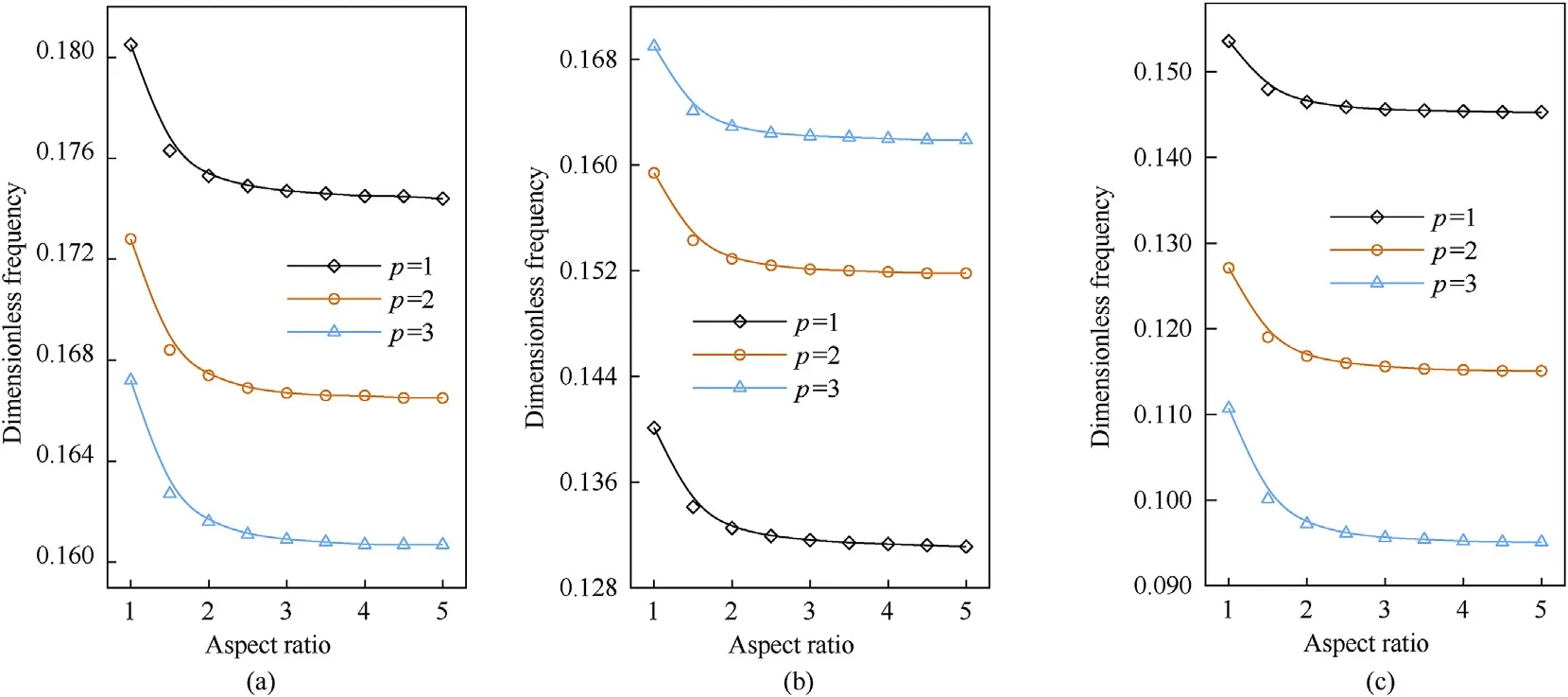
Fig.14.Dimensionless frequencies versus the aspect ratio;(a): X distribution,(b): O distribution,(c): V distribution.(SSSS,N ＝1, a/h ＝10, ＝0.17).

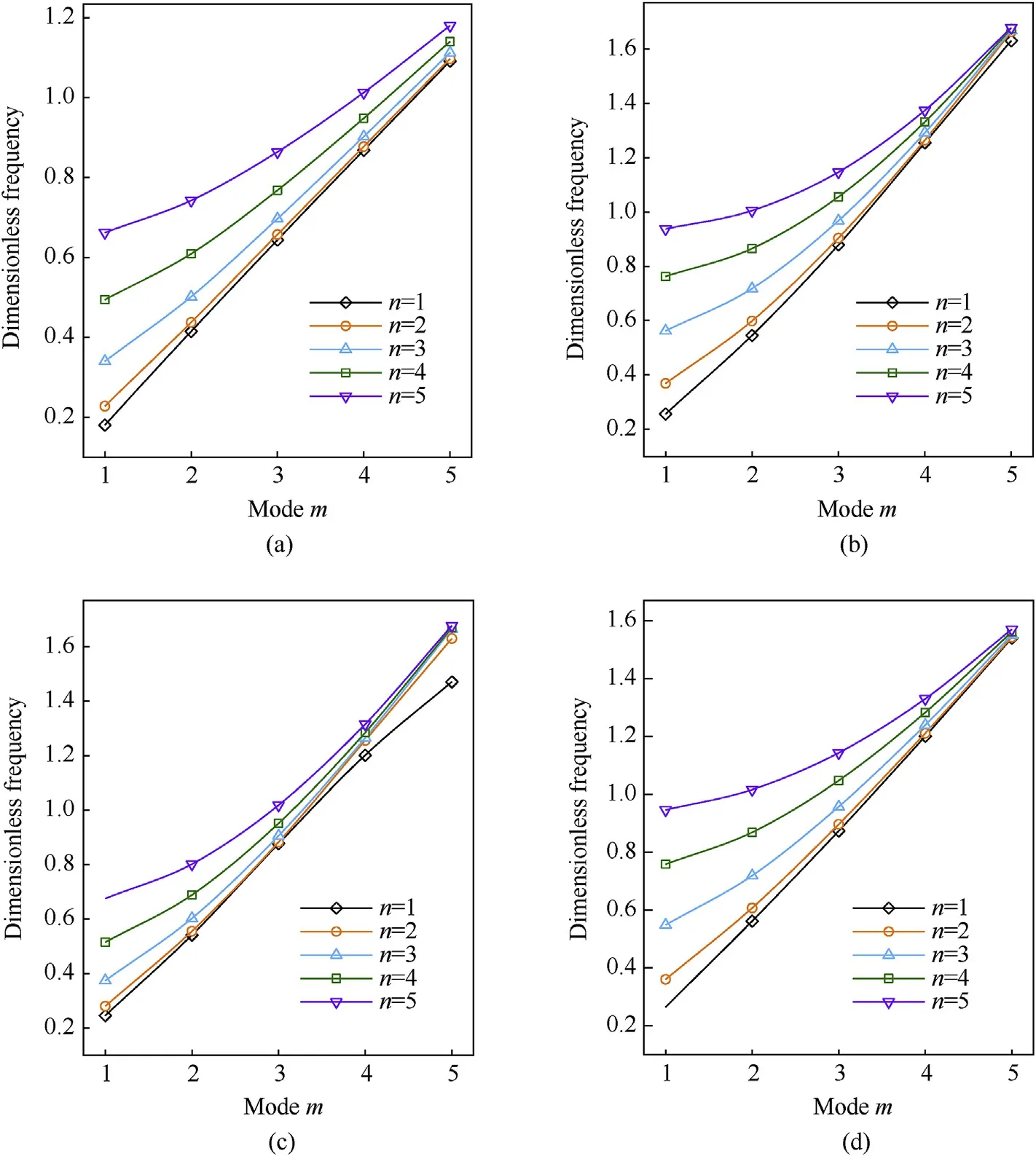
Fig.15.Effect of vibration modes of square FG-X plates;(a): SSSS,(b): CCCC,(c): CSCS,(c): CCSS (n ＝1,a/h ＝10).(SSSS,N ＝1,a/h ＝10, ＝0.17).

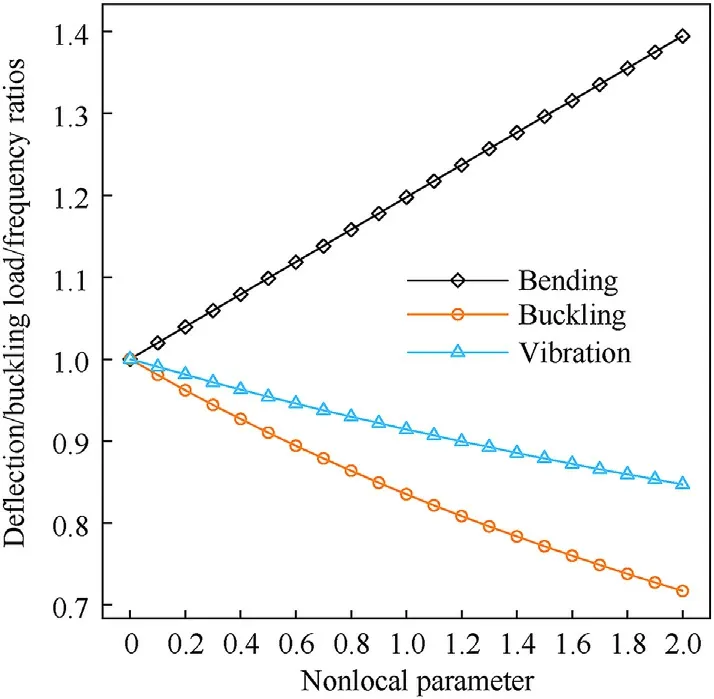
Fig.16.Effect of nonlocal parameter on the deflection,critical buckling load,and fundamental frequency ratios for a simply supported square FG-X CNTRC plates（p ＝1,λ ＝0 nm,N ＝1,a/h ＝10, ＝0.17）.

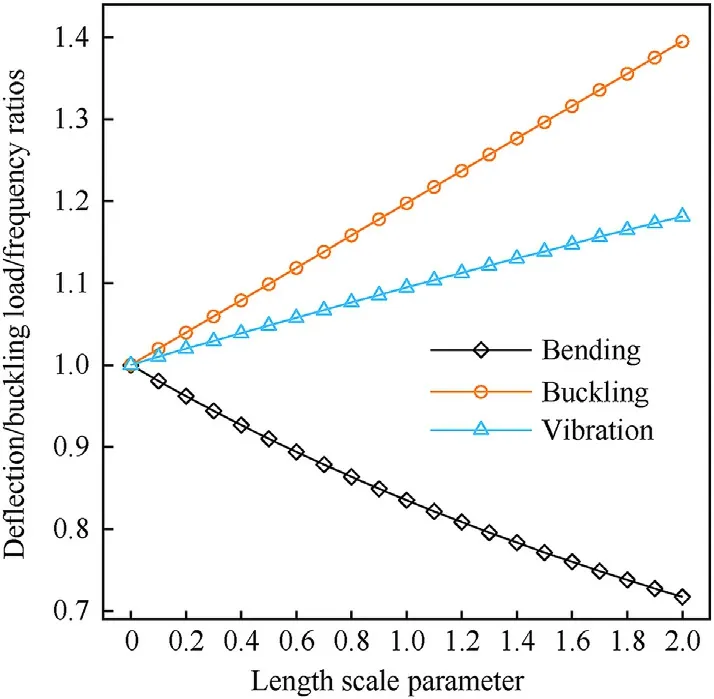
Fig.17.Effect of length scale parameter on the deflection,critical buckling load,and fundamental frequency ratios for a simply supported square FG-X CNTRC plates（p ＝1,N ＝1, n ＝1,μ ＝0 nm,a/h ＝10, ＝0.17）.

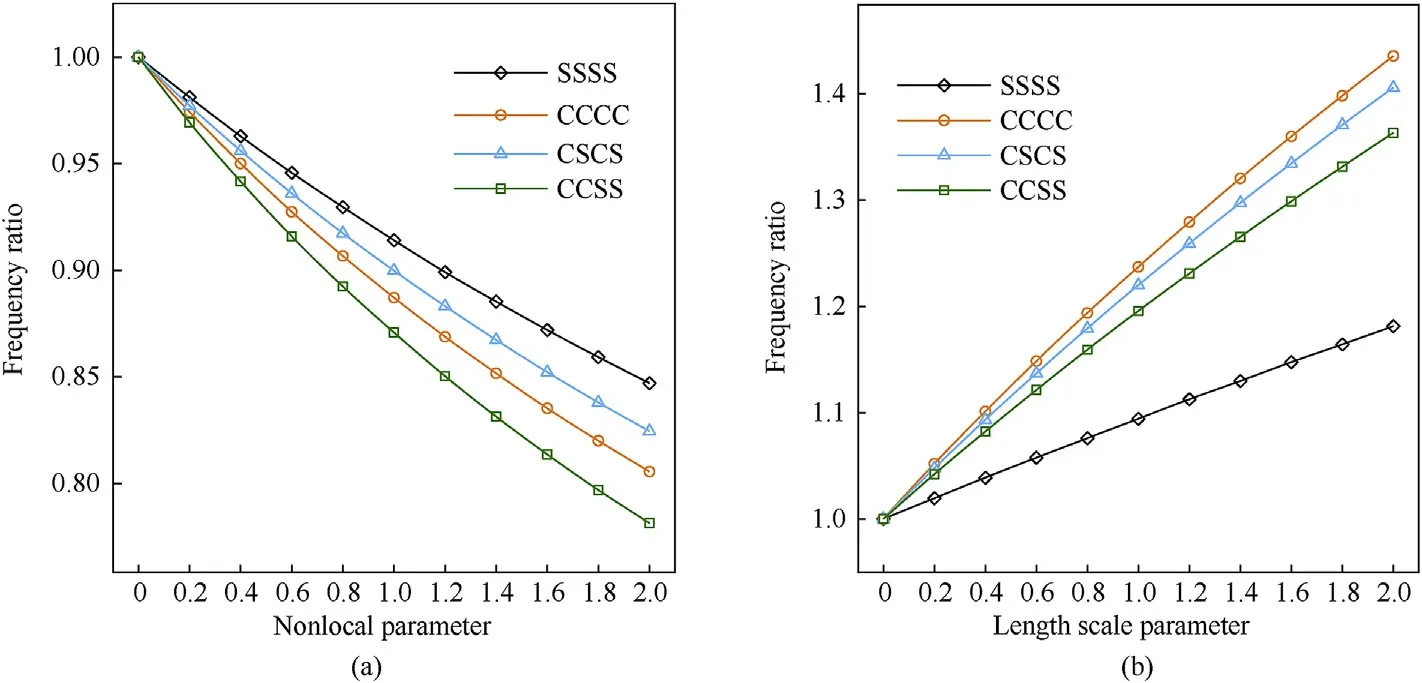
Fig.18.Influence of (a): nonlocal parameter（λ ＝0 nm）,(b): length scale parameter（μ ＝0 nm）and boundary conditions on the fundamental frequency ratios for FG-X CNTRC plates (p ＝1,N ＝1,b/a ＝1,a/h ＝10, ＝0.17).

Fig.19.Influence of(a):nonlocal parameter（λ ＝0 nm）,(b):length scale parameter（μ ＝0 nm）and the thickness parameter(a/h)on the fundamental frequency ratios for simply supported square FG-X CNTRC plates (p ＝1,N ＝1, ＝0.17).

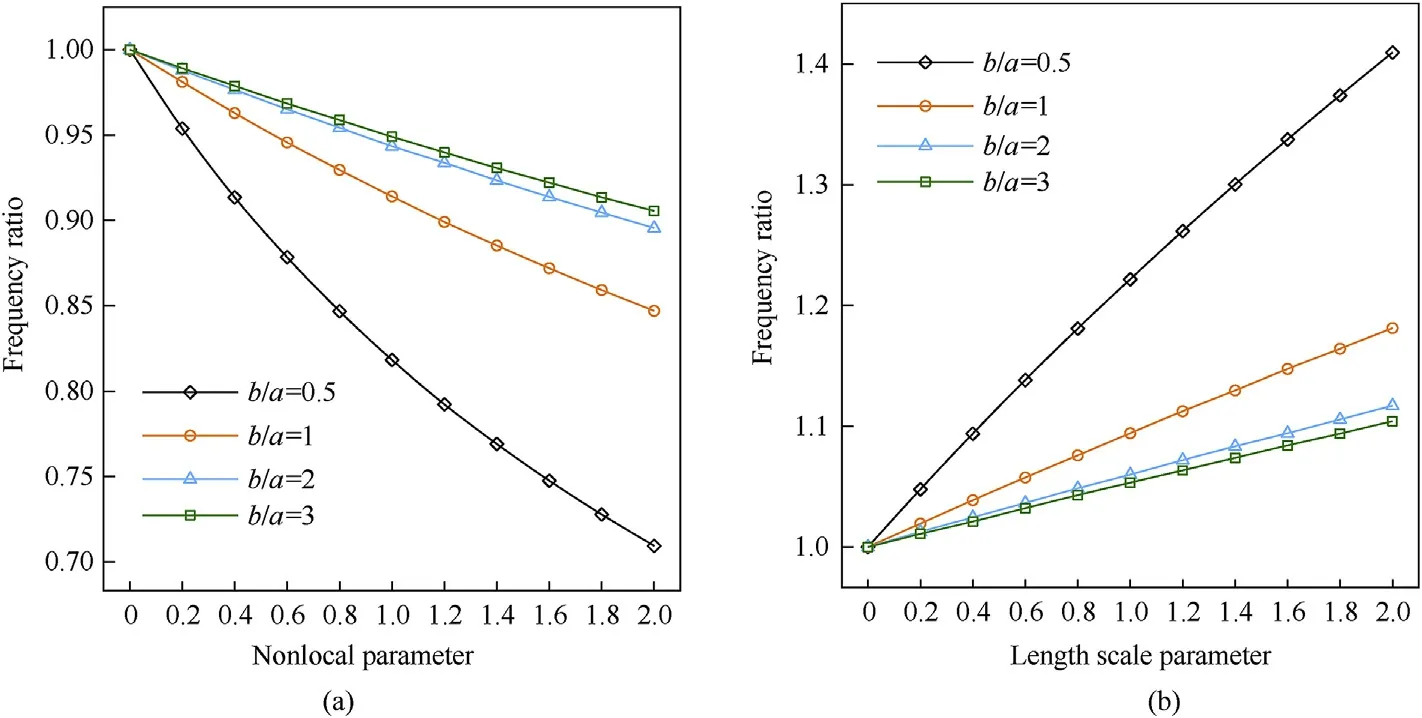
Fig.20.Influence of (a): nonlocal parameter（λ ＝0 nm）),(b): length scale parameter（μ ＝0 nm）and the aspect ratio (b/a) on the fundamental frequency ratios for a simply supported square FG-X CNTRC plates (p ＝1,N ＝1, a/h ＝10, ＝0.17).

· The response of the CNTRC plates is considerably influenced by the applied boundary conditions.

Finally,this work plays a significant role for further studies in composite plates using 3D elasticity model.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This research was supported by The Algerian General Directorate of Scientific Research and Technological Development(DGRSDT)and University of Mustapha Stambouli of Mascara(UMS Mascara) in Algeria.

Rigidity matrix elements;