Influence of shaped charge structure parameters on the formation of linear explosively formed projectiles

Tian-bao Ma,Jing Liu,Qi Wang

State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing,100081,China

Keywords:LEFP Numerical simulation Shaped charge Structure optimization

ABSTRACT The research of LEFP (linear explosive forming projectile) is of great value to the development of new warhead due to its excellent performance.To further improve the damage ability of the shaped charge warhead,a special shell overhanging structure was designed to increase the charge based on the traditional spherical charge,in which case the crushing energy of LEFP could be guaranteed.LS-DYNA was used to simulate different charge structures obtained by changing the number of detonation points,the length of shell platform,the radius of curvature and the thickness of liner.The RSM(response surface model) between the molding parameters of LEFP and the structural parameters of charge was established.Based on RSM model,the structure of shaped charge was optimized by using multi-objective genetic algorithm.Meanwhile,the formation process of jet was analyzed by pulsed X-ray photography.The results show that the velocity,length-diameter ratio and specific kinetic energy of the LEFP were closely related to the structural parameters of the shaped charge.After the optimization of charge structure,the forming effect and penetration ability of LEPP had been significantly improved.The experimental data of jet velocity and length were consistent with the numerical results,which verifies the reliability of the numerical results.

1.Introduction

With the improvement of the protection capabilities of modern military equipment,traditional shaped charges are facing great challenges.In the field of active protection,a new type of shaped energy warhead named linear explosively formed projectiles(LEFP)have been proposed in recent years,which is developed on the basis of traditional Explosively Formed Projectile (EFP).Compared with traditional EFP,it has higher speed,quality and hit rate.

Payman[1] first proposed a structure similar to EFP in 1935.At the end of the 20th century,EFP was widely concerned by researchers [2-4].The study found that the shape of the EFP was main affected by the shape and material of the liner,the type and detonation method of the explosive,the structure and geometric parameters of the shaped charge.Weickert[5]studied the process of seven different shapes of liner penetrating targets of different materials,and found that the penetration ability of EFP was greatly affected by the shape of the liner.Houman[6]used a shape function with a correction term to optimize the shape of the EFP,the measured speed and profile of EFP were in good agreement with the optimization results.In addition,Jacek [7] compared the formation process of the EFP with conical charge and spherical charge,and the experiments of penetrating steel target were carried out.Pappu [8] and Zhu [9] used AUTODYN to study the residual microstructure characteristics and geometric parameters of EFP formed by liner in different materials.They found that tantalum material is more conducive to the formation of EFP.While Wu[10],Hu[11,12]and Zaki[13]studied the influence of different explosive materials and liner shapes on the penetration capability of EFP,the best combination of liner and explosive was obtained.Meanwhile,Li [14] found that annular multi-point initiation was more conducive to the improvement of EFP＆apos;s penetration ability,but the multipoint synchronized initiation deviation needed to be less than 200 μs.In terms of the structure of shaped charge,the penetration performance of EFP was mainly improved by connecting two liners in series [15] or multi-stage ammunition [16].

In order to further enhance the penetration capability of projectile,scholars were committed to exploring new shaped charge warhead.Literature [17-19] proposed an appropriate model to study the dynamic response of structure driven by explosion from a theoretical perspective.Liu [20] conducted penetration tests of a new type of multi-explosively formed projectile warhead (MEFP)with seven arc-cone liners against 45#steel target.In addition,the influence of the structural parameters of MEFP warhead on the formation of EFPs was studied in literature [21].Bohanek [22]determined the effects of different qualities and materials of explosive on the penetration ability of LEFP through experiments.Cheng[23]designed a new bi-apex-angle linear shaped charge,the effects of different liner thickness and explosive type on jet penetration performance were studied.

Ning [24] and Ma [25] proposed a special evolvable warhead structure as illustrated in Fig.1.This evolvable warhead was symmetrical and consists of four similar parts,which would be expanded under explosion loading and the fragments with a directional distribution were generated to increase the damage effect.To further enhance the penetration performance to thicker targets,a linear shaped charge warhead was proposed in this paper based on the reference [25].The forming process of LEFP was numerically simulated by LS-DYNA,and the influence of initiation method,the length of shell platform,the radius of curvature and the thickness of the liner on the forming of LEFP were analyzed.Moreover,an optimization scheme was designed to optimize the geometric parameters of the shaped charge to improve the penetration ability of LEFP.This will have a certain impetus for future research on LEFP.

2.Material model and parameters

2.1.The calculation model

In this paper,the forming of LEFP and penetration into the target were studied.The calculation model consists of four parts: shell,explosive,liner and air.The structure of shaped charge is shown in Fig.2.

The appearance of the shaped charge designed is cylindrical,with a diameter of 20 cm and a height of 30 cm.Four identical linear liners are symmetrically distributed around.The linear liner is divided into 10 segments,the outermost two segments have a height of 2.0 cm,the middle eight segments have a height of 3.0 cm,and the cover have a thickness of 1.0 cm.Due to the symmetry of the structure,a quarter model is used for calculation.The size of the air domain,meanwhile,is 200 mm × 400 mm × 550 mm with continuous boundary condition.Fig.3 shows the internal structure of the model.The structure is composed of shell,cover,explosive and a liner.Where L is the length of shell platform,and δ are the radius of curvature and thickness of the liner,respectively.

Fig.1.The structure of evolvable warhead.

Fig.2.The structure of shaped charge.

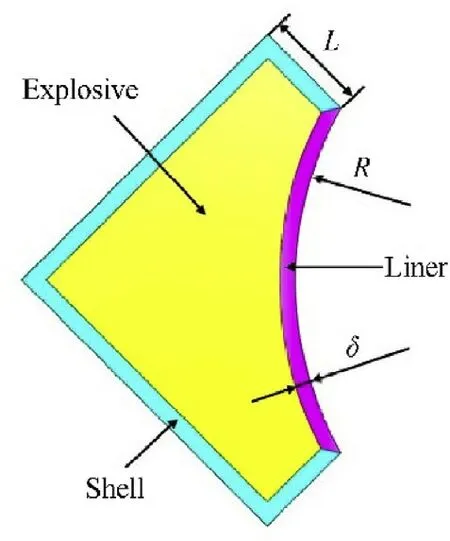
Fig.3.The internal structure of the model.

The calculation model was simulated by LS-DYNA software.The grid size of the shell and air is 1.5 mm,while the liner and explosive are 1.0 mm.The numerical Algorithm is ALE(Arbitrary Lagrangian-Eulerian),in which the shell and liner are Lagrangian grids,explosive and air are Euler grids.

2.2.Material model and parameters

The materials of the shell,liner and target involved in this paper are aluminum,copper and 45# steel.They are modeled by the Johnson-Cook material model which is widely used in the research of penetration.The yield stress σis defined as:

To describe the material at a high strain rate,the equation of state of Gruneisen is used in the above three parts.The pressureis defined as:

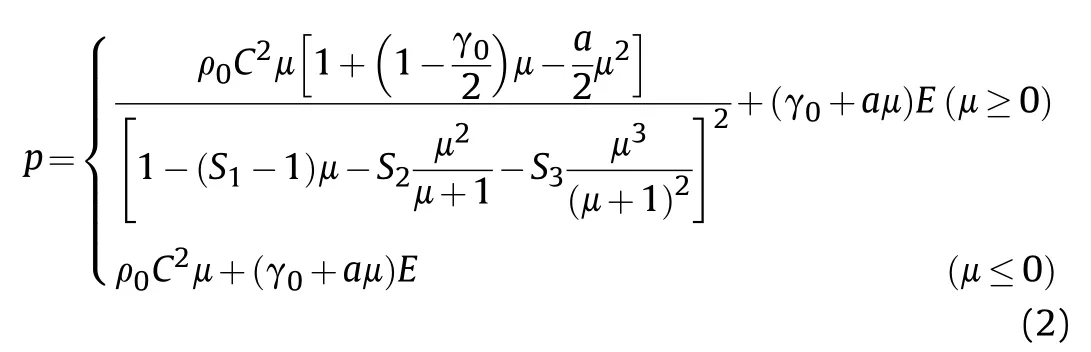
where ρis the initial density.is the intercept of the v-vcurve.,andare the coefficients of the slope of the v-vcurve where vand vare shock-velocity and particle-velocity,respectively.γis the Gruneisen gamma.The first order volume correction for γis.And μ ＝ρ/ρ-1.represents internal energy.

Explosive studied in this paper is Comp-B,high-energy material model and JWL equation of state are adopted,in which the pressureis expressed as:

where,,,and ω are parameters related to the explosive.is the specific volume.is the specific internal energy.

Numerical computation is carried out in the air domain,and the equation of state of air is Linear-Polynomial.The pressis given by:

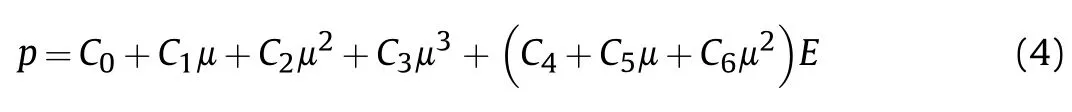
where,…are the coefficients of polynomial equation.μ ＝ρ/ρ-1,and ρ/ρis the ratio of current density to initial density.is the internal energy.

The material parameters of copper and aluminum are determined by separate Hopkinson pressure bar (SPHB) experiments,the parameters of different material models are listed in Table 1.

2.3.Numerical algorithm and experimental verification of shaped charge jet

(a) The model of shaped charge jet

The calculation model is shown in Fig.4,where the explosive is Comp-B,the length of the charge is 110 mm,the diameter is 60 mm.The thickness of the liner is 2.4 mm,with a diameter of 60 mm,with a conical angle of 60.Numerical calculations are carried out in the air domain.The calculation domain is cylindrical with a length of 280 mm,and its diameter is 100 mm.The axis of the explosive and the liner is the same as the calculation domain due to the symmetry of the model.

LS-DYNA was used for numerical calculation,the calculation method was ALE,in which the liner was Lagrangian grid,the explosive and air were Euler grid.The size of the Lagrangian grid is 0.3 mm,while the Euler grid is 0.4 mm.Such grid size could ensure the accuracy of calculation effectively.

Fig.4.3D structure of shaped charge jet.

Fig.5.The jet of shaped charge.

To ensure the reliability of numerical results,the experiment of jet flow was carried out.Pulsed X-ray photography could measure the process of high-speed movement,which was widely used in explosion experiments.It was used to observe the formation process of the jet,obtain the velocity of the jet tip and measure the length of the jet.Both experiment and numerical calculation were single-point initiation,and which was located in the center of the end face of the explosive.In experiments and numerical calculations,it could be clearly seen that the liner was crushed by the detonation products,and finally a pestle body and a metal jet were formed.At＝26 μs and＝42 μs,the images taken by pulse X-ray photography were shown in Fig.5(a),and the numerical results were shown in Fig.5(b).The results data were listed in Table 2.

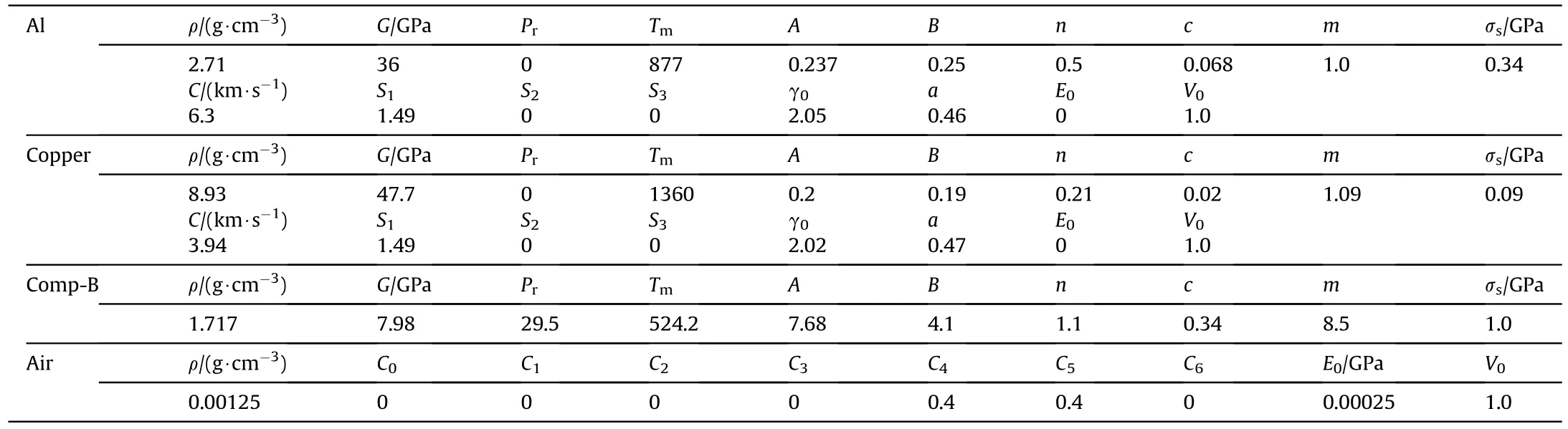
Table 1 Parameters of each material.

Table 2 Material model in the table.

Analyzing the data in the table,the error of the jet length was 1.0%when＝26 μs,which was 1.4%when＝42 μs.The error forboth the diameter of the jet and the velocity of the jet tip was less than 6.0%.When the jet becomes stable,the shape of the jet was in good agreement with the experimental result.This showed that the numerical method was very effective for the simulation of the jet and could be used to simulate the experimental results.

3.Numerical simulations on the forming of LEFP

3.1.Analysis of the formation process of LEFP

Numerical results showed that in the process of being crushed of the 10-segment liner,the two segments at the edge with a large scattering angle had poor forming effect as shown in Fig.6.The eight segments at the middle had better forming effect,especially the two segments in the middle.On the basic of this,the middle two segments were used to be analyzed.

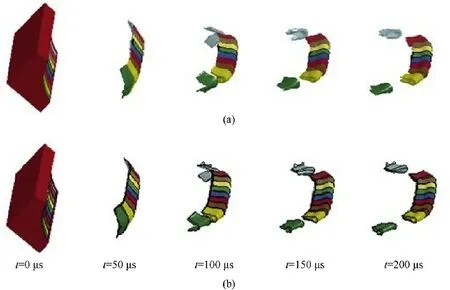
Fig.6.The forming of LEFP: (a) R ＝10 cm,δ ＝4.5 mm, L ＝3 cm;(b) R ＝10 cm,δ ＝4 mm, L ＝3 cm.

The forming process and the overall velocity curve of the intermediate EFP were shown in Fig.7 and Fig.8.The crushing,overturn and closing of EFP could be clearly seen in Fig.7.About＝170 μs,the shape of LEFP had been stabilized,and then it kept the same shape to fly.From Fig.8,the velocity increased dramatically in the first 20 μs,and then it flattened out in the next 80 μs.The curve tended to stabilize after 80 μs which suggested that the velocity reached a stable value.

The control variable method was used to design the structure parameters of the shaped charge and the number of detonation points.The stable velocity (),the specific kinetic energy () and the length-diameter ratio(＝/)of LEFP were used as indicators to assess penetration ability.The stable velocityrefers to the subsequent stable value of the velocity curve in Fig.8,and the specific kinetic energy＝/,whereis the kinetic energy of EFP andis the projected area in the flight direction of the EFP.Fig.9 was a schematic diagram of the definition of parametersand.

3.2.The influence of the number of detonation points on LEFP molding

The model＝10 cm,δ ＝4.5 mm,＝3 cm was selected,and six groups of samples with the number of detonation pointsranging from 3 to 8 were designed.When＝200 μs,in which moment the LEFP had been formed stable,the curves of velocity,specific kinetic energy and the length-diameter ratio varying with the number of detonation points were obtained,as illustrated in Fig.10.

According to Fig.10,it could be found that as the number of detonation pointsincreases,the velocity and specific kinetic energy of LEFP had a little change.They had a small growth when the number of detonation points increased from 3 to 4,and then the curves flattened out.The length-diameter ratio of LEFP increased slowly when the number of detonation points was no more than 6,while increased obviously whenexceeded 6.The results showed that with the increase of the detonation points,it was close to the line detonation,the impact of the detonation wave on the liner was more balanced.This led to the liner being crushed better,which led to a better molding effect of the LEFP.

3.3.The influence of the length of shell platform on LEFP molding

Choosing L ＝2.0,2.125,2.25,2.375,2.5,2.625,2.75 and 3.0 cm when＝10 cm,δ ＝4.5 mm and＝8,eight groups of samples were designed.The curves of velocity,specific kinetic energy and the length-diameter ratio varying with the length of shell platform were obtained at＝200 μs,as shown in Fig.11.

According to Fig.11,asincreased from 2.0 cm to 3.0 cm,the velocity of LEFP increased steadily,with an increase of 17.9 %.Nevertheless,the specific kinetic energy fluctuated around 40 kJ/cm.The reason was that with the increase of,the mass of the explosive also increased,which led to a certain increase in the velocity.Due to the particularity of the structure,the mass of the liner will decrease,and there was little difference in the kinetic energy of the LEFP,which led to a small increase in the specific kinetic energy.Before L reaches 2.5 cm,the length-diameter ratio decreased with the increase of,and then it fluctuated around 2.9 asincreased.It could be seen from No.7-14 in Table 3,when2.5 cm,the shape of LEFP was long,while≥2.5 cm,the length of LEFP was close to the same.When L is less than 2.5 cm,the velocity of LEFP was small although the length-diameter ratio was large.In comparison,the molding of LEFP was better whenwas around 3.0 cm.

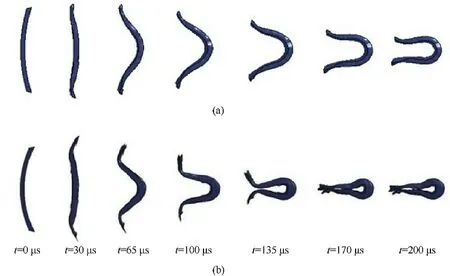
Fig.7.The forming process of LEFP: (a) R ＝15 cm,δ ＝4.5 mm, L ＝3 cm;(b) R ＝10 cm,δ ＝4.5 mm, L ＝3 cm.

Fig.8.The velocity curve of LEFP in model R ＝10 cm,δ ＝4.5 mm,L ＝3 cm.

Fig.9.Definition of parameters of LEFP.

3.4.The influence of the radius of curvature of the liner on LEFP molding

Ten calculation examples were designed with＝5,7.5,10,12.5,15,17.5,20,22.5,25 and 30 cm when δ ＝4.5 mm,＝3 cm and＝8.The velocity,specific kinetic energy,and length-diameter ratio curves with the radius of curvature of the liner were obtained when＝200 μs,as shown in Fig.12.

From Fig.12,as the radius of curvatureof the liner increased,the velocity increased significantly and specific kinetic energy of LEFP went up and then it went down.Whenincreased from 5 cm to 10 cm,the velocity increased greatly,and then it tended to be flat whenreached 10 cm.The specific kinetic energy reached its maximum whenwas around 10 cm.The length-diameter ratio decreased as the radius of curvature of the liner increased.As can be seen from No.15-24 in Table 3,with the increased of,the bending of the liner decreased as same as being stretched.Therefore,the length of the LEFP was shorter and the thickness was larger,which was not conducive to the penetration of the LEFP.It could be found that when the radius of curvature of the liner was around 10 cm,it was beneficial to improve the penetration ability of LEFP.

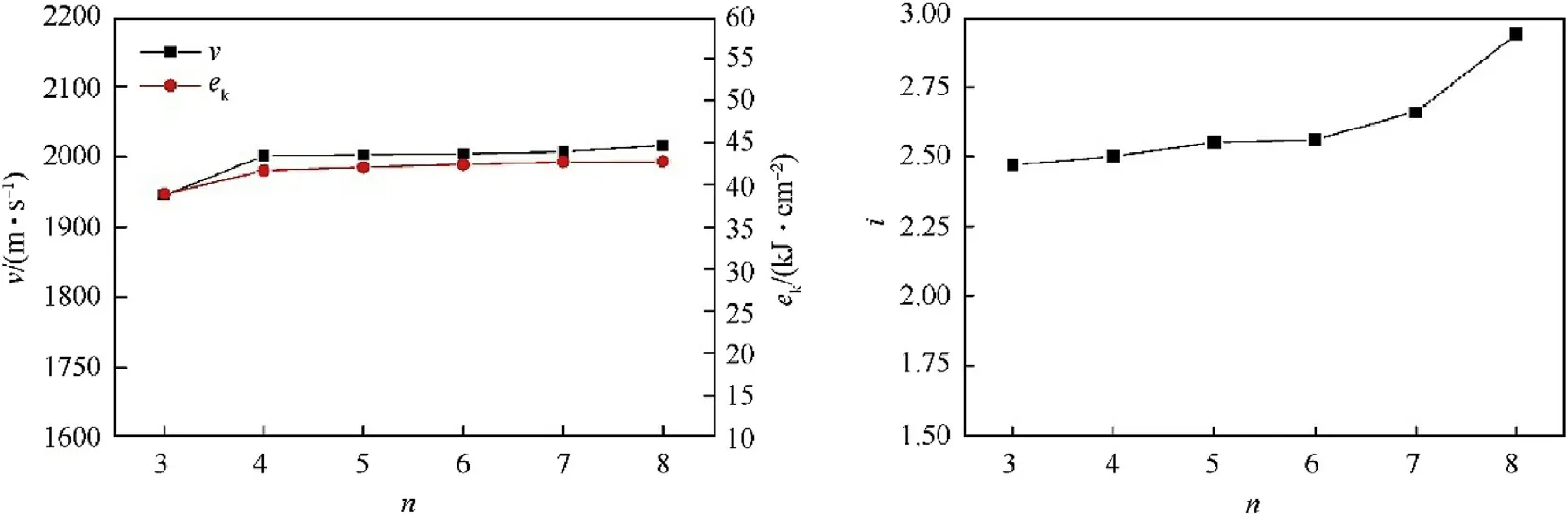
Fig.10.The curves of v, ek and i varying with n.

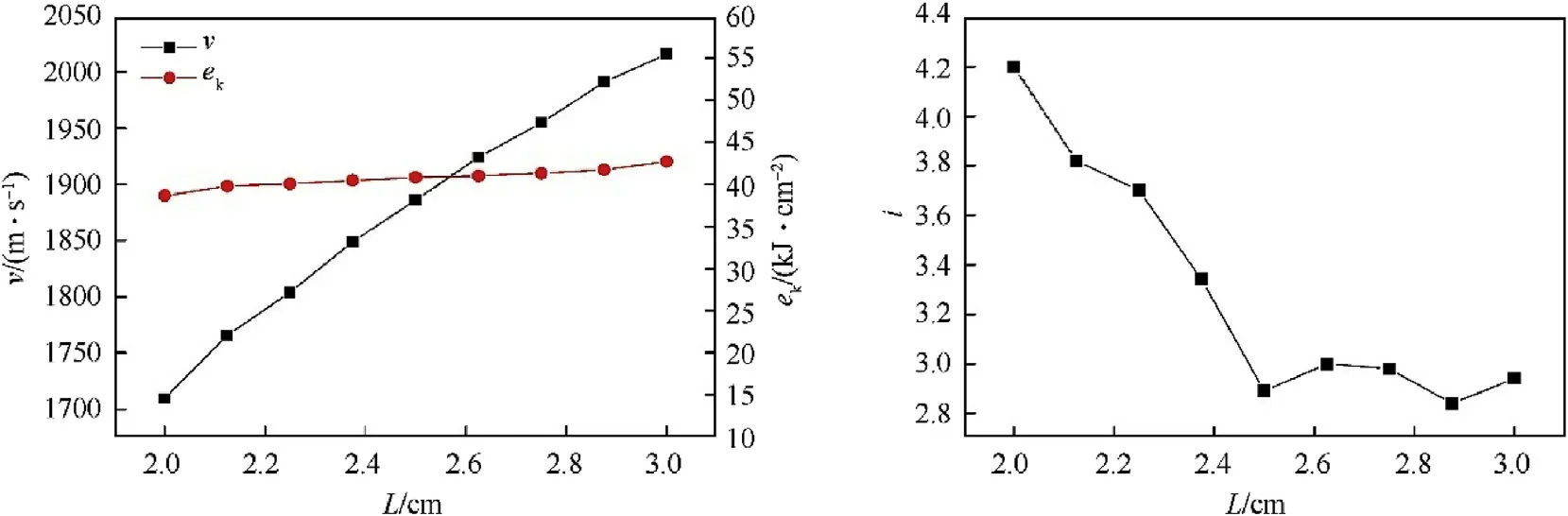
Fig.11.The curves of v, ek and i varying with L.

3.5.The influence of the thickness of the liner on LEFP molding

Nine numerical examples of δ ＝3.5,3.75,4.0,4.25,4.5,4.75,5.0,5.25 and 5.5 mm were selected when＝10 cm,＝3 cm and＝8.The curves of the velocity and specific kinetic energy and length-diameter ratio varied with the thickness of the liner(δ)was obtained at＝200 μs as Fig.13.

From the analysis in Fig.13,the mass of the liner increased with the thickness of the liner increased,which led to a significant downward trend in the velocity and specific kinetic energy of LEFP.During the change of δ from 3.5 mm to 5.5 mm,the velocity decreased from 2371.8 m/s to 1761.3 m/s and the specific kinetic energy of LEFP reduced from 64.17 kJ/cmto 34.76 kJ/cm,which was adverse to the penetration of LEFP.The length-diameter ratio of LEFP first increased and then decreased with the increase of δ,reaching the maximum value when δ was near 4.5 mm.According to No.25-32 in Table 3,it was found that when δ was around 4.5 mm,the shape of LEFP was longer and thinner.For comprehensive comparison,it was good for the formation of LEFP when δ was in the vicinity of 4.5 mm.

3.6.Analysis and discussion of numerical simulation results

Analyzing the above numerical calculation results and combined with the final molding effect of middle EFP as shown in Table 3,it could be concluded that when＝10 cm,δ ＝0.45 cm,＝3.0 cm and＝8,the molding effect of the LEFP were optimal.Meanwhile,it had a higher velocity,a relatively large specific kinetic energy and length-diameter ratio.

4.Structural parameter optimization design

4.1.Establishment of response surface model

According to the numerical results,the number of initiating points was kept at 8.In order to obtain a more accurate mathematical model,10 additional points created by Optimal Latin-Hypercube Design [26,27] were added to build the model.The length of shell platform,the radius of curvatureand the thickness δ of the liner were regarded as input variables.Based on the numerical results in the previous section,the range of input variables was further refined as Table 4.The middle LEFP was used for analysis,and the numerical results of the increased sample points were shown in Table 5.

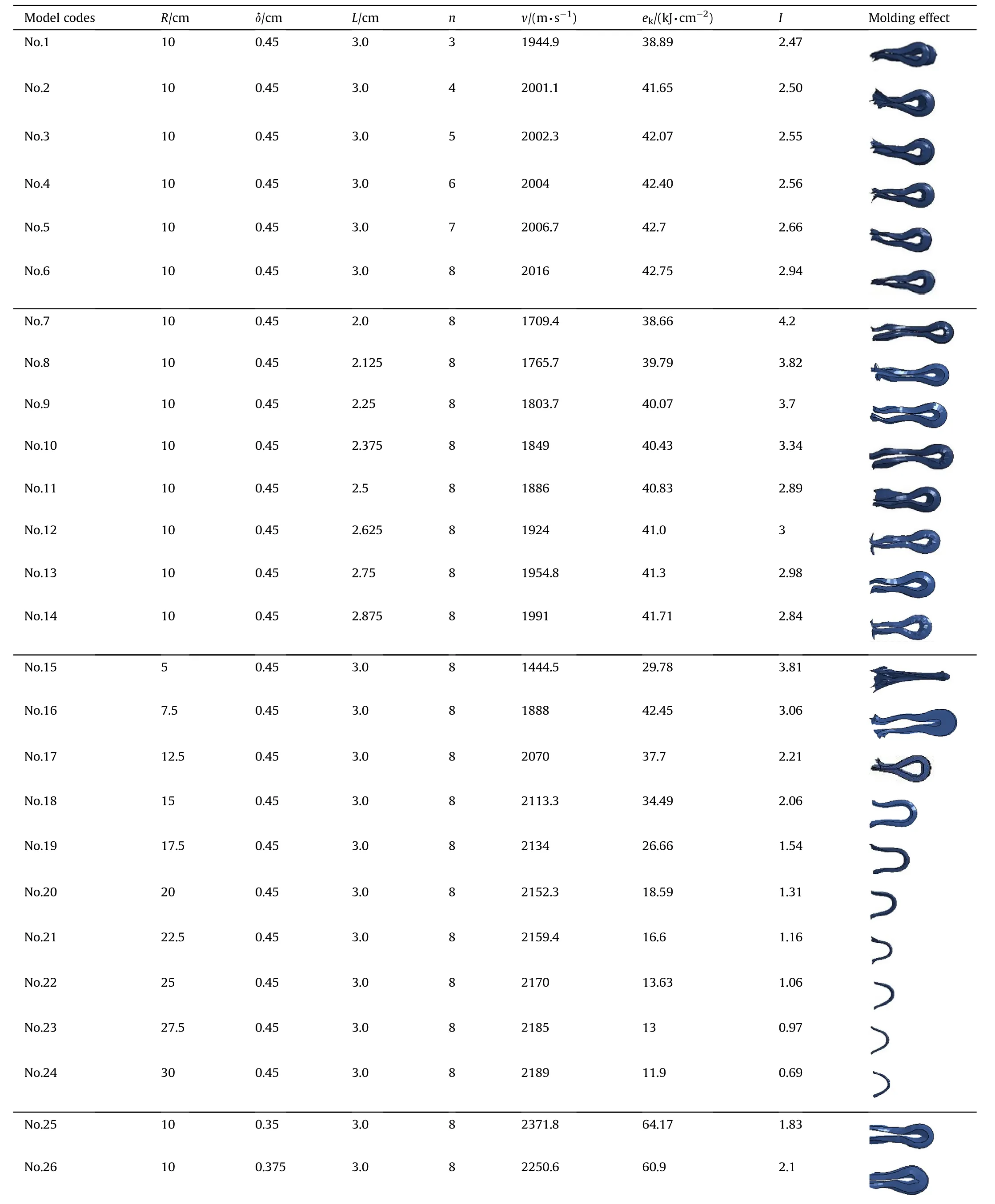
Table 3 Forming results of LEFP.

Table 3 (continued)

Table 4 Design scope of parameters.

Table 5 The numerical simulation results.

Correspondingly,the velocity,specific kinetic energy and length-diameter ratio of the LEFP were regarded as output variables.Third-order response surface models of three output variables with respect to input variables were established by Matlab software as Eqs.(5)-(7).This method used polynomials to fit the sample points,which was more accurate in the local scope and simple to calculate.

4.2.Error analysis of the model

There are three indicators for evaluating model accuracy: Coefficient of Multiple Correlation (),Relative Average Absolute Error () and Relative Maximum Absolute Error ().They are expressed as equations 8-11:

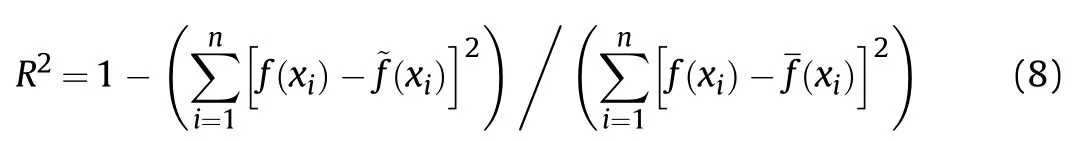
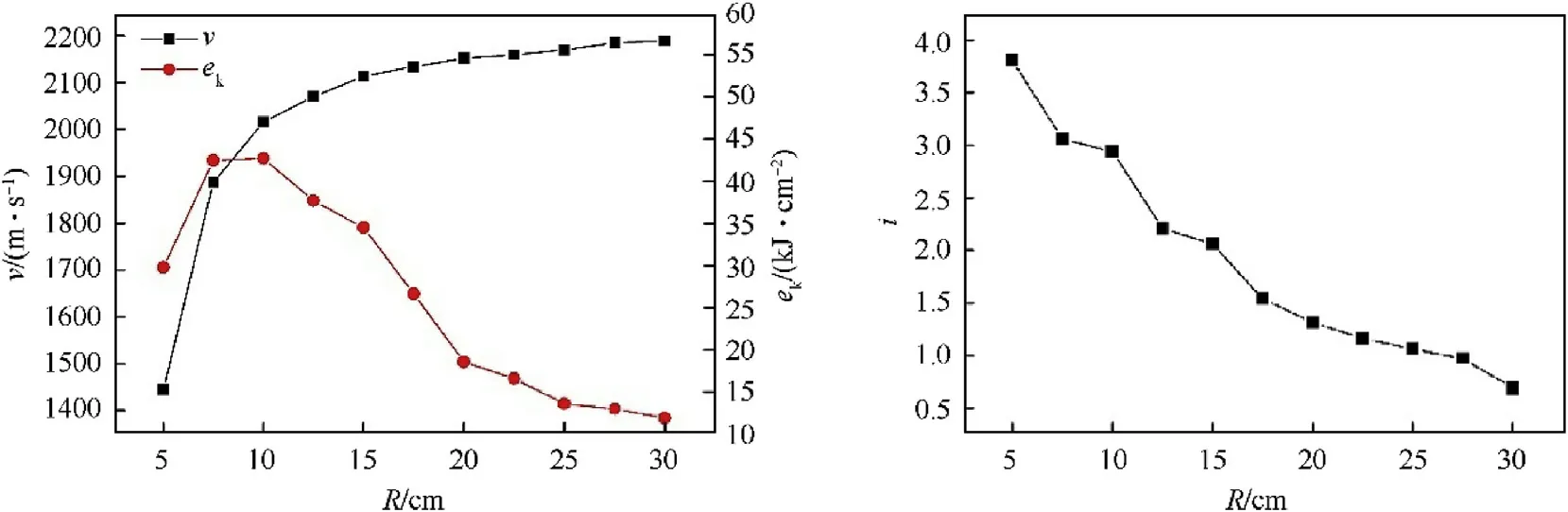
Fig.12.The curves of v, ek and i varying with R.

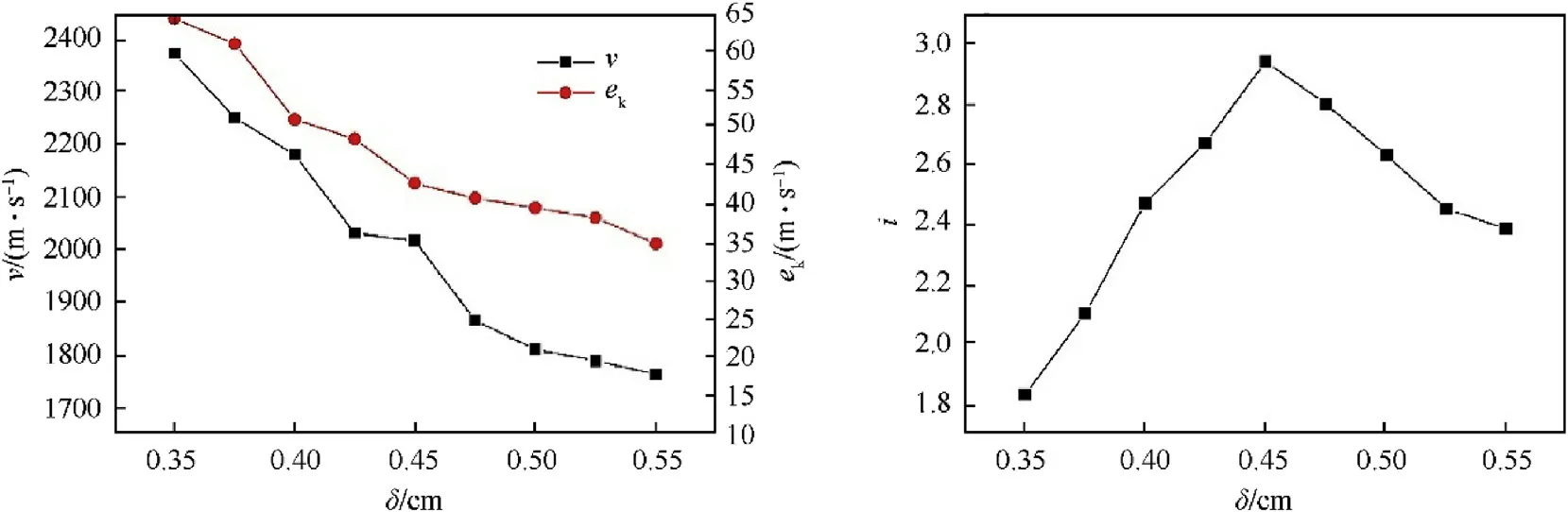
Fig.13.The curves of v, ek and i varying with δ.

,andare used to jointly evaluate the accuracy of the model.andevaluate the accuracy of the model globally,andevaluates the accuracy of the model locally.The closeris to 1,the smaller the value ofand,and the more accurate the model is.The reference ranges of,andare 0.9-1,0 to 0.2,and 0 to 0.3 respectively.Five points were randomly selected for error analysis of the model,and the error was shown in Table 6.

To further verify the accuracy of the model,a test point far from the center of the sample were selected for numerical simulation.The test point was＝10 cm,δ ＝0.35 cm,＝2.5 cm.The numerical results and calculation results were shown in Table 7.

It could be found from Table 7 that the model calculation results were in good agreement with the numerical results,and the mathematical model could reflect the numerical simulation results very well.

4.3.Optimization scheme design

Sequential Quadratic Programming (NLPQL) [28,29] is an algorithm widely used in optimization design.It expands the objective function with a second-order Taylor series,and linearizes the constraints.The original nonlinear problem is transformed into a quadratic programming problem,and this algorithm is very stable.The mathematical model is as

whereand（）are input and output variables,andare the numbers of them.（）and（）are equality constraints andinequality constraints,andare the numbers of them.andindicate the lower and upper bounds of the input variable as listed in Table 4.The input variablein this paper were the length of shell platform,the radius of curvatureand the thickness δ of the liner,and the output variable（）were the velocity,specific kinetic energyand length-diameter ratioof EFP.Inequality constraints（）were applied in optimization scheme,and（）were designed as≥2000 m/s,≥50 kJ/cm,and≥3.5.

Table 6 The error analysis.

Table 7 The test point results.

Table 8 The results before and after optimization.

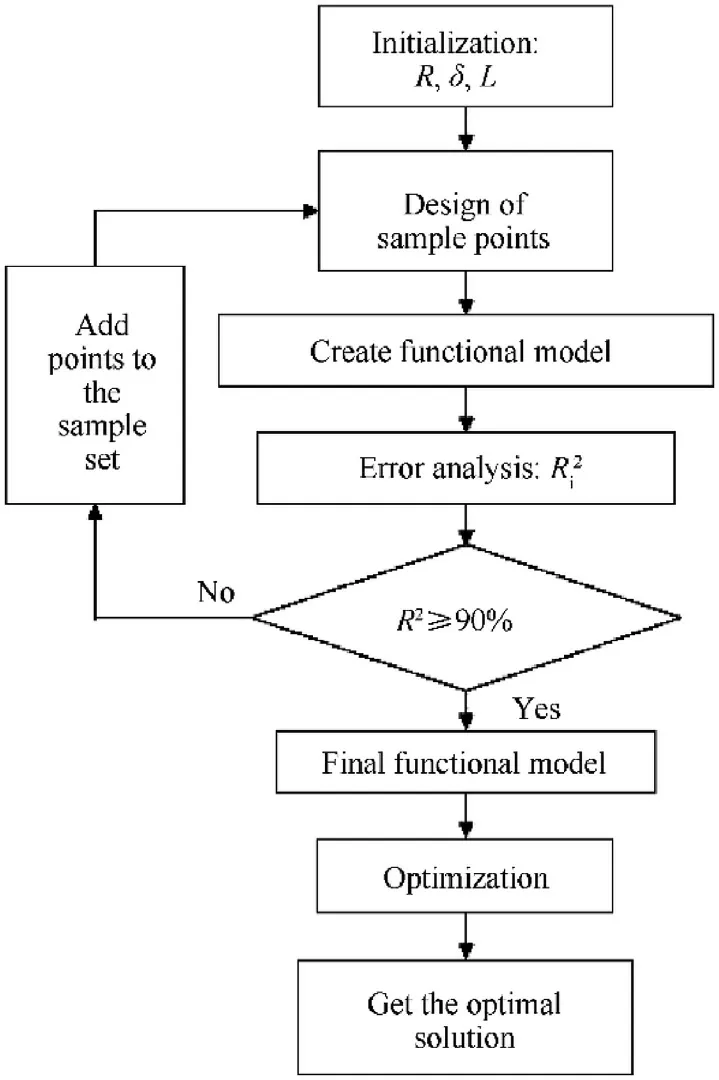
Fig.14.Optimization process.

Based on iSight software,the sequential quadratic programming method was carried out in this paper for iterative optimization,the number of iteration steps was set to 100.The length-diameter ratio and specific kinetic energy became the main optimization goal,and the velocity became the auxiliary optimization goals by assigning weighting coefficients.The structure parameters of the shaped charge based on the maximum value of the objective function were obtained.The process was shown in Fig.14.The initial parameter was＝10 cm,δ ＝4.5 mm,＝3.0 cm.The optimized result was＝11.75 cm,δ ＝3.66 mm,＝2.0 cm.

Fig.15.Forming of LEFP before and after optimization: (a) Before optimization;(b) After optimization.

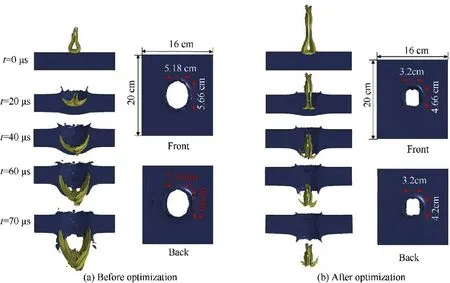
Fig.16.The effect of penetration.

4.4.Numerical simulation results of penetrating steel target

Numerical simulation of the optimized model was compared with the initial model.Analysis of intermediate EFP found that the velocity,kinetic energy and length-diameter ratio of LEFP had been greatly improved.The forming process of LEFP before and after optimization was shown in Fig.15,and Table 8 showed the numerical results.

It could be seen from Fig.15 that the optimized liner was crushed by the detonation product and turned faster,which was more conducive to the formation of LEFP with a large lengthdiameter ratio.It also could be found from Table 6 that compared with initial model,the length-diameter ratio of LEFP had increased by 77.55 % after optimization,and the velocity and specific kinetic energy had also increased by 2.5%and 49.86%,respectively.Which was due to the large length-diameter ratio and specific kinetic energy as the main optimization goal.

Fig.17.The residual velocity of LEFP.

Table 9 The results before and after optimization.

Based on the results before and after optimization,the process of penetrating the steel target with a thickness of 3 cm was simulated.The penetration effect of the middle EFP was shown in Fig.16.

Fig.16 illustrated the length-diameter ratio of LEFP was relatively small before optimization,and the pits of the target were large,which was caused by the serious deformation of LEFP during the penetration.After optimization,the length-diameter ratio of LEFP increased,the deformation of the LEFP decreased during the penetration,and the target had smaller pits,which ensured the remaining penetration capability of the LEFP.

The fragments of the LEFP were collected for residual velocity analysis as shown in Fig.17.Where vand vwere the velocities before and after optimization.It could be concluded that the decay time of vwas shorter than v,which indicated that the penetration process took less time and retained a higher residual velocity after optimization.

The data of velocity decay was listed in Table 9.Analysis of Table 9 showed that compared with before optimization,the absolute velocity decay of LEFP was reduced by 190 m/s,the relative velocity decay was reduced by 10.86 % after optimization.The penetration ability of LEFP had been greatly improved.

5.Conclusion

In this paper,a series of numerical simulations on shaped charges of different structural sizes were carried out by using LSDYNA.The RSM of the velocity,the kinetic energy and the lengthdiameter ratio of LEFP with respect to the number of detonation points,the length of shell platform,the radius of curvature and the thickness of the liner were obtained.An optimization method was designed to optimize the better model.The main conclusions are as follows:

(1) Compared with the pulse X-ray experiment,the numerical results were in good agreement with the experimental results.The numerical simulation results can be used to approximate the experimental results within a certain range.

(2) Analysis of numerical simulation results,when the number of initiation points is more than six,it has little effect on the forming of LEFP.Within the scope of the research,the velocityand specific kinetic energyof LEFP increase with the length of shell platformincreases,and decrease with the increase of the thickness of the liner δAs the radius of curvatureof the liner increases,the velocity increases but the specific kinetic energy increases first and then decreases.The length-diameter ratiodecreases whenandincrease,it increases first and then decreases with the increase of δWhen L exceeds a certain value,the length-diameter ratio tends to be stable.

(3) The sequential quadratic programming method is used to optimize the established third-order response surface model,and accurate result is obtained.Numerical simulations of penetrating steel target are carried out before and after optimization.The results show that the velocity,specific kinetic energy and length-diameter ratio of LEFP have improved,especially the specific kinetic energy and lengthdiameter ratio have increased greatly.Based on the analysis of the residual velocity of fragments,both the absolute velocity decay and relative velocity decay of the optimized LEFP are reduced,which is conducive to the improvement of the penetration performance of the LEFP.It illustrates the reliability of the optimization method.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was supported by the National Natural Science Foundation of China (Grant No.11772061).