Thermal explosion of a reactive gas mixture at constant pressure for non-uniform and uniform temperature systems

Saad A.El-Sayed

Mechanical Power Engineering Dept.Zagazig University,Zagazig,Alshrkia,Egypt

Keywords:Thermal explosion Approximate solution Critical conditions Distributed and uniform temperature systems

ABSTRACT In this study,the approximate and exact solutions for the stationary-state of the solids model with neglecting reactant consumption for both non-uniform and uniform temperature systems were applied on gas ignition under a constant pressure condition.The criticality conditions for a slab,an infinite cylinder,and a sphere are determined and discussed using dimensionless temperatures under constant ambient and surface temperatures for a non-uniform temperature system.Exact solution for a Semenov model with convection heat loss was also presented.The solution of the Semenov problem for constant volume or density as a solid and constant pressure were compared.The critical parameter δ is calculated and compared with those of Frank-Kamenetskii solution values.The validation of the calculated ignition temperatures with other exact solution and experimental results were offered.The relation between critical parameters form Semenov and F.K.models solution was introduced.

1.Introduction

The self-ignition problem using thermal explosion theory was proposed firstly by Semenov et al.[1].He obtained the critical criterion of chemical thermal runaway through calculating the tangent point of exothermal and cooling curves(critical point)for a uniform temperature system.Frank-Kamenetskii et al.[2]extended the theory to a non-uniform temperature system considering temperature distribution inside the system and heat transfer with a heat source in the reaction zone.However,the boundary condition of Frank-Kamenetskii model belongs to Dirichlet boundary condition,which limit the application of this model.To simplify the critical problem,Frank-Kamenetskii assumed that the geometry of reactant is a simple geometrical symmetric shape as infinite plates,infinite cylinders or spheres [3].Frank-Kamenetskii [4] extended Semenov theory to what we called the distribution temperature system.He considered the internal thermal resistance but neglected the boundary thermal resistance.Kordylewski [5] considered the critical criterion δas a bifurcation point of the energy conservation equation according to bifurcation theory offered by Ref.[6].Shouman et al.[7-9] revised the criticality when the reactant consumption were taken into consideration and discussed the cases of neglecting the reactants depletion for the uniform systems.Boddington et al.[10-12] investigated critical conditions by proposed a correction of criterion of criticality for both uniform and non-uniform temperature systems.Their treatments revised the criteria of criticality in general boundaries for the exponential approximation suggested by F.K.In addition,Rice et al.[13] also analyzed the criterion of criticality based on the thermal explosion theory.The gas thermal explosion of the case of distributed temperature geometries(slab,cylinder,and sphere)by using a shooting method combined with a Newtonian-Raphson technique and certain boundary value expansions was studied in Ref.[14].Ignition parameters were obtained for the true Arrhenius equation and the effect of ambient temperature on them is determined and discussed.Critical values at critical conditions for various geometries are determined by using the Hermite-Pad′e approximants method in Refs.[15,16].It is known that,the critical conditions depend on the size,the shape geometry,and the heat transfer to the surroundings,as well as on the ambient temperature in which the material is being stored.The approximated approaches proposed that the critical conditions can be evaluated at the maximum temperature or at the average temperature of the solid.Saad A.El-Sayed[17]investigated analytically and numerically the critical and transition conditions of gaseous explosion in different planes of solution.Analyses of thermal explosion in combustible gas mixtures containing fuel droplets extended to permit a more general temperature dependence of reaction rate for most typical practical reactions under physically realistic assumptions presented in Ref.[18].Semenov and Thomas models employed to analyze the criticality of battery thermal runaway in uniform and non-uniform temperature distribution situations in Ref.[19].Campell [20] studied numerically the thermal explosion in a spherical reactor with neglecting the effect of consumption reactant under the influence of natural convection,where the effects of natural convection on thermal explosion have considered and the temperature of the wall of the reactor held constant.They showed that the temporal development of the maximum temperature in the reactor was qualitatively similar as the Rayleigh and Biot numbers were varied.Also,importantly,the maximum temperature in a stable system was shown to vary with the Biot number.Zhang et al.[21] established thermal explosion models of cylindrical battery which consider a non-uniform heat dissipation of the lateral surface and different heat dissipation of top and bottom surfaces.The influence of Biot number on the critical parameters was investigated and the critical thermal explosion ambient temperatures were determined.Soliman [22] introduced an approximate analytical solution for Frank-Kamenetskii equation modeling a thermal explosion of a sphere.For the original boundary value problem and for a given FrankKamenetskii parameter,a nonlinear algebraic equation needs to be solved until to be able to apply the approximate solution.Harley and Momoniat [23] examined the steady state solutions of a heat balance equation modeling a thermal explosion in a cylindrical vessel.The classical Lie group analysis of differential equations is used to obtain the well-known solution of Frank-Kamenetskii for a cylindrical vessel.Olanrewaju et al.[24]investigated the effect of geometry on the thermal explosion of a strong exothermic chemical reaction with variable pre-exponential factor under Arrhenius and other forms of reaction rates with neglecting the reactant consumption.Harley and Momoniat [25]solved the thermal explosion model by using the Lane Emden equation for a cylindrical geometry.The critical value of Frankkamentskii parameter δ of value 2 is obtained.Filimonov and Koshelev [26] proposed a new criterion for thermal explosion in exothermically reacting systems.They found that the dependence of the maximum temperature on the Semenov and Todes parameters is bitable and the critical conditions can be determined by the extremum conditions on the diagrams.Er-Riani1,Chetehouna[27]applied the homotopy perturbation method for solving the steady state equations of the combustible material obeying Arrhenius and other laws of reaction rates.Their equations are formulated on some of class A geometries(an infinite cylinder,an infinite slab and a sphere).They also investigated the effect of Frank-Kamenetskii parameter δ on the thermal criticality by means of the Domb-Sykes graphical method.Anderson and Zienkiewicz [28] investigated the steady-state and transient ignition of thermal explosion problem by using the finite element method.The steady-state discretized equations are solved by an incremental Newton-Raphson procedure using the Frank-Kamenetskii parameter δ as the incremented or“loading”variable.Critical values of the Frank-Kamenetskii parameter δ were obtained for both common and unusual shapes.S′anchez-Rodriguez et al.[29] analyzed the condition needed for thermal explosion to occur when the surface temperature of the vessel walls is raised at a constant rate.Analytical expressions for the critical condition as a function of the system parameters for different geometries were obtained.Fine et al.[30] applied the thermal theory of spontaneous ignition on diethyl peroxide and temperature measurements in the verge of ignition were studied.The experimental Frank -Kamenetskii parameter δ and the critical temperatures under the effect of environmental temperatures were determined.Gray et al.[31]investigated the spontaneous ignition of gaseous diethyl peroxide as a thermal explosion by a series of experiments mainly in a cylindrical vessel,and including diluted mixtures.A critical center temperature rise exists above which ignition is unavoidable.A similar agreement between measured and theoretically expected values for F rank-Kamenetskii＆apos;s parameter δ was found.

In the present study,the same approximations that known before will use for investigating the stationary-states critical conditions of thermal explosion of both non-uniform and uniform systems of gases at constant pressure.Both F.K.and Semenov models were used in this study and the F.K.approximation for the Arrhenius rate equation was used.The critical parameters and critical conditions are determined for both models with investigating the limiting cases of the solution.The study covers two cases: a known surface temperature (constant) and a convection cooled boundary to constant ambient temperature.Analytical expressions were developed and applied on practical problems.

2.Mathematical foundation

The Fourier balance equation(distribute temperature)for a onedimensional,non-uniform temperature distribution and a zero order gaseous reaction in which the pre-ignition reactant consumption is negligible is introduced.Assuming that the thermal reaction obeys Arrhenius form and the pressure is constant,this equation can put in the following form

For stationary-state,Eq.(1a) becomes

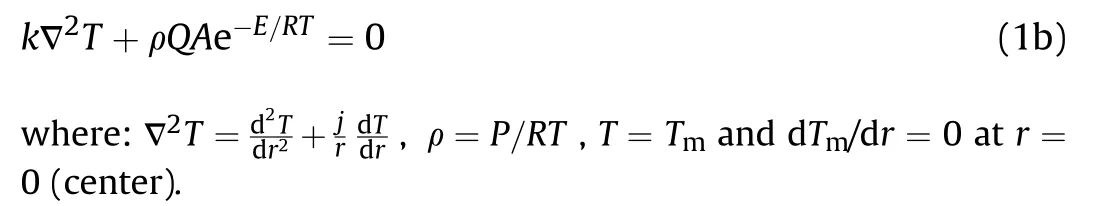
Note that:is the reactant gas temperature,K;is the time,s;ρ is the gas density,kg/m,is the specific heat,kJ/kg K;is the heat of reaction J/kg,is the frequency factor,s;is the activation energy,J/kg;is the thermal conductivity,J/K·m·s;is the universal gas constant,J/K·kg;is the gas pressure,J/m;is the radial distance,m;andis the maximum temperature.

Setting Eq.(1b) in the dimensionless form becomes

For adiabatic case∇θ ＝0,so the adiabatic temperature can obtained from Eq.(2) as

For stationary-state case,Eq.(2) becomes

where θ ＝is dimensionless temperature,ξ ＝(PQAR/kE)r,is the dimensionless parameter of the system relating the heat generated during the chemical reaction and the heat drained away by conduction(the shape factor) ＝0,1,2,for slab,cylinder,and sphere respectively,τ ＝/（（）/）is the dimensionless timeWhen the reaction is fast and highly exothermic,and the conduction loss is small,ξ has a large value and the opposite is true.

For Tylor series about ξ ＝0,

This solution considers that,the heat generation term does not depend on position but depends only on the maximum central temperature θalthough it is not known but it cannot be constant and can consider the most dominant parameter in the chemical reaction.The reason for that,any slight increase in the temperature(in the order of 20 K) at the center will produce thermal runaway reaction[30,31].Thus,θcan determined from the known surface temperature (θ) boundary condition,where at wall ξ ＝Х and θ ＝θ,then Eq.(7) can put as

For convection boundary condition,at thin wall（θ-θ）＝（θ-θ）where θcan be computed from it if both θand θare known.Bothandcan be obtained from Nusselt number empirical equations or from tables.From Eqs.(7)and(8),we can get the temperature distribution with position within the vessel as(Figs.1 and 2)

So,for traditionally convection cooled boundary condition,at ξ ＝

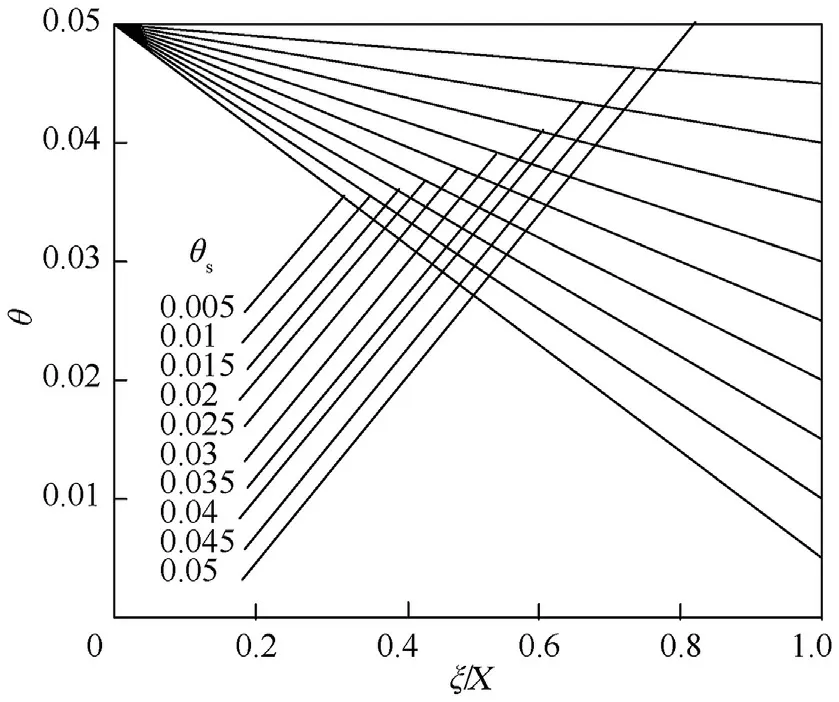
Fig.1.Shows θ vs.ξ/X at θm ＝0.05 and different values of θs.

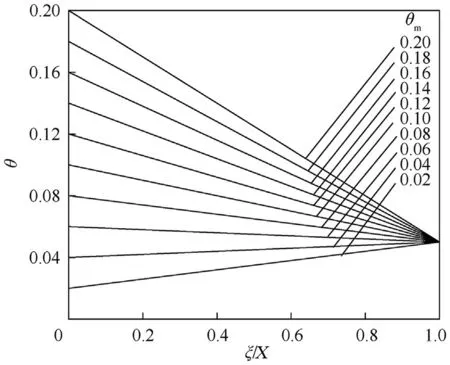
Fig.2.Shows θ vs.ξ/X at θs ＝0.05 and different values of θm.

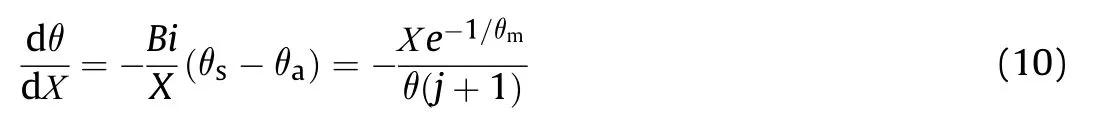
Substituting Eq.(8) into (10),produces

Eq.(11)represents the convection cooled to a constant ambient temperature,where＝is the Biot number.Dividing Eq.(8)on Eq.(11) and after arrangement,one can get

As we go away from the surface(ξ＝1.0)(see Figs.1 and 2),the θ value increases until reaches the highest value at the vessel center(ξ＝0.0).For θ＝θ,the relation between them is a horizontal line (upper horizontal-axis) and as θdecreased,the values of θ decreased at the same dimensionless distance (ξThis because the rate of heat transfer to the surrounding is less.At constant θ,θ values decrease as we travelled away from the surface towards the center of the vessel when θ＜θand the opposite is true when θ＞θBecause the heat released or generated due to chemical reaction becomes higher and so does the gas temperature inside the vessel.

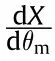
The critical thicknesscan obtained from Eq.(14) as

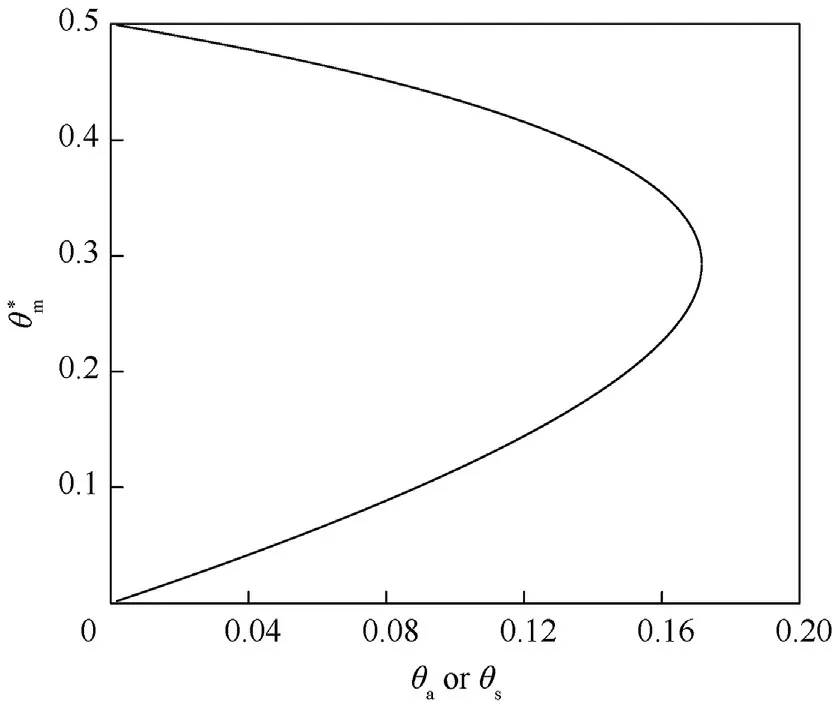
Fig.3.Shows vs.θa or θs.

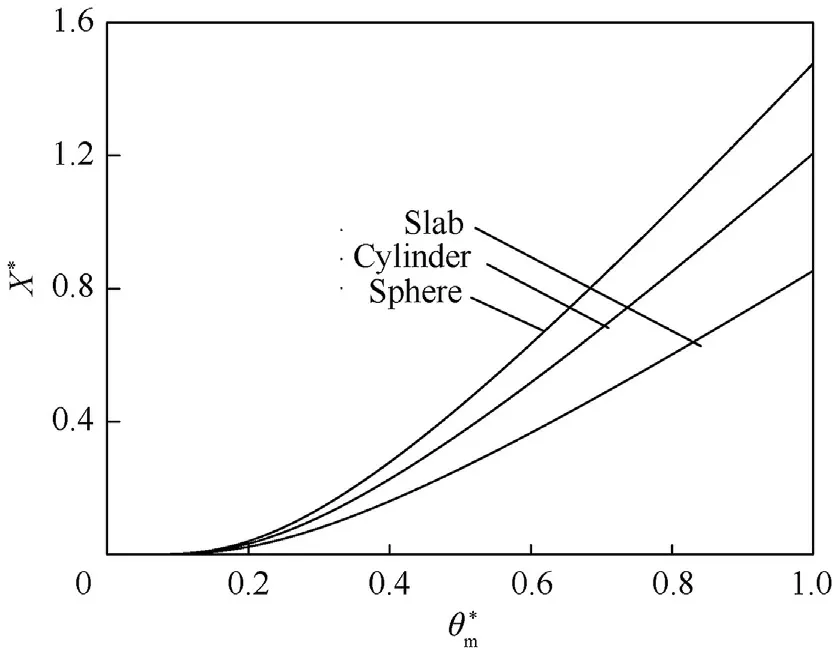
Fig.4.Shows Х* vs for slab,cylinder,and sphere.

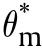
which is equivalent to following equation

If the average temperature θis considered instead of the central maximum temperature θ,so Eq.(9)can be used to obtain the following equat

The integration of Eq.(18),assuming that the heat generation term is only dependent on θinstead of θ,yields

Fig.5.vs for different Biot number.

Considering that surface area＝π（2ξ）where＝1,2πξ,4πξfor slab,cylinder,and sphere,respectively,the solution of the problem can be obtained as

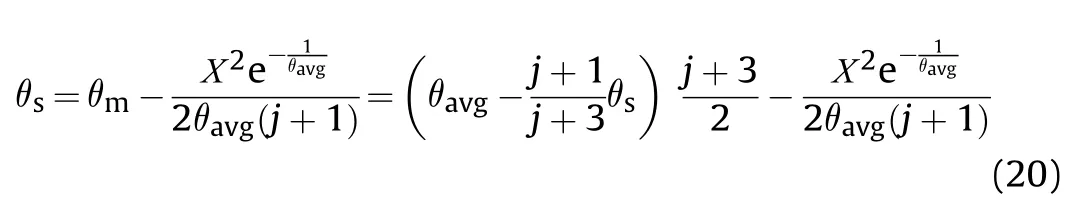
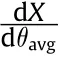
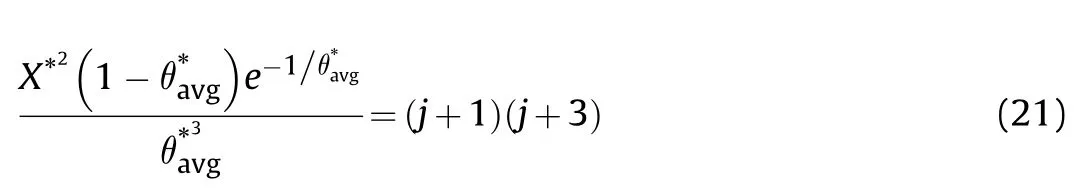
Using the convection cooling boundary condition where the ambient temperature is constant,Eq.(21) becomes

Using Eq.(20),the final form of solution (average critical ignition temperature) can be put in the following form

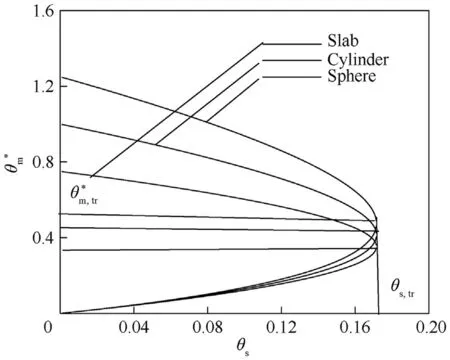
Fig.6. vs θs for slab,cylinder,and sphere.

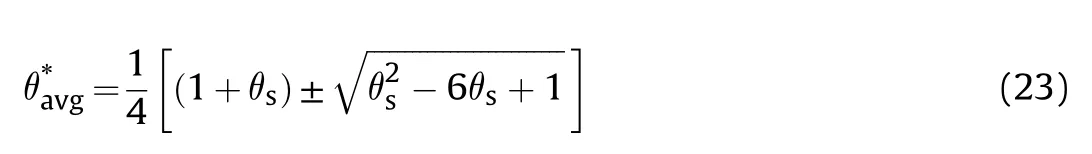
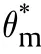
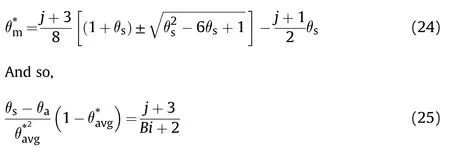
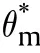
For traditionally convection cooled (Newtonian -cooled)boundary condition,at ξ ＝δ

Substituting Eq.(29) in Eq.(28),yields

Dividing Eq.(28) by Eq.(30) gives

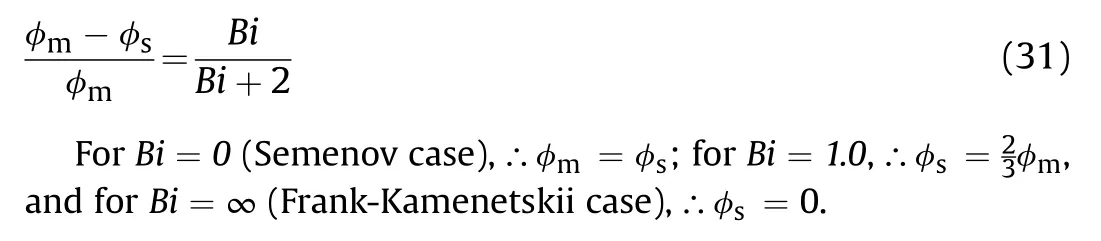
The critical condition can be obtained by differentiating δ with respect to φin Eq.(28)and equating the result to zero,that yields

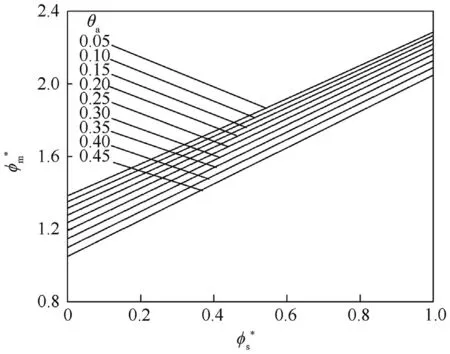
Fig.7. vs for different values of.θa.

For a seek of comparison,spontaneous ignition of gaseous dialkyl peroxide in a cylindrical vessel under a maintained vacuum of 10Torr [30] compared against the analytical solution in the present work.The properties of diethyl peroxide are＝27±1.3 kJ/(K·m·s),＝197 ± 4.0 kJ/mol,＝151-157 kJ/mol.

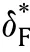
For traditionally convection cooled boundary condition,the critical conditions can be obtained by differentiation δ with respect to φin Eq.(30)and equating the result to zero,which produces

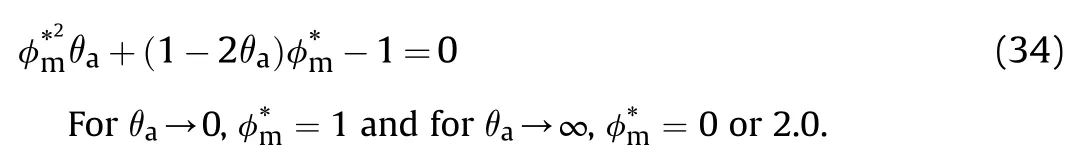
Substituting Eq.(31) into Eq.(34) yields

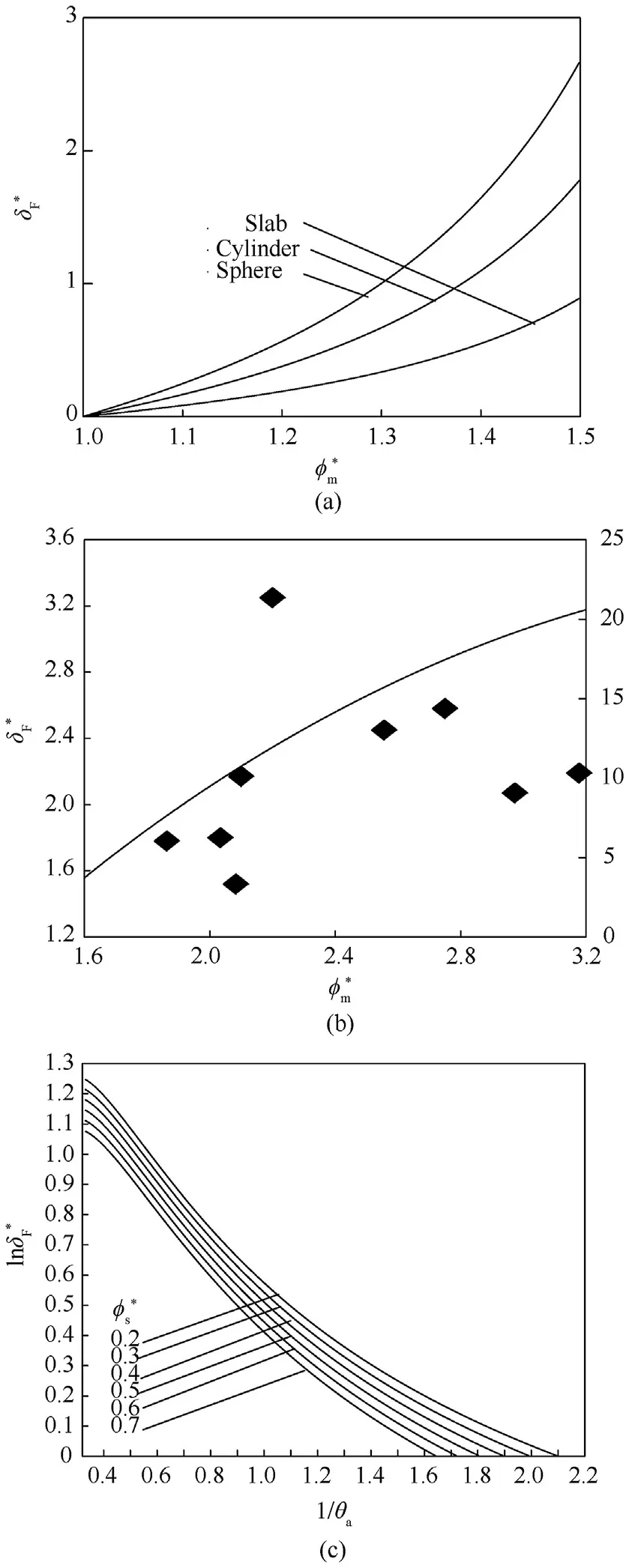
Fig.8.a vs for slab,cylinder,and sphere,b comparison between analytical solutionand experimental work [33].c ln -1/θa for different .

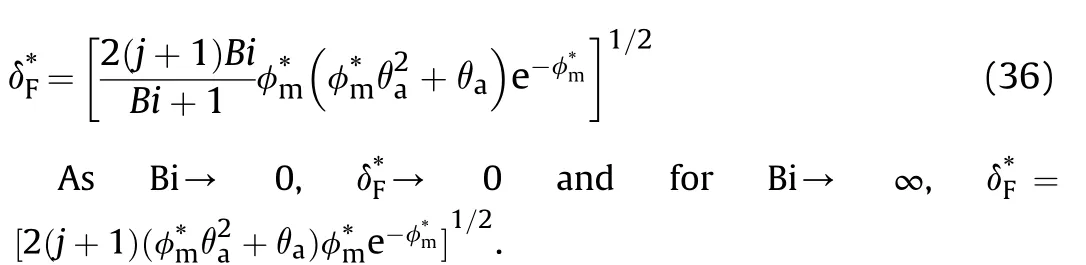
Fig.9. vs.θa.

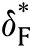
For a seek of comparison,the thermal decomposition of azomethane was considered for a simulation of numerical investigation of the effect of natural convection beside the external heat transfer (Biot number) of a gas thermal explosion at constant wall temperature and constant concentration under steady-state condition in Ref.[19].The physico-chemical properties employed were:＝2250 J/kg·K,＝1.24 × 10molms,＝23,280 K (so＝193.6 kJ/mol).The exothermicity of the reaction was assumed to be＝124 kJ/mol and the ambient temperature equals 636.2 K.

Fig.11.Comparison between analytical solution and experimental work [20].The diamonds are for cases with Ra (Rayleigh number) ＝103,the squares represent Ra ＝104 and the triangles are Ra ＝105 for different modes of natural convections.

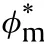
Considering the case of Semenov of zero order reaction and the temperature distribution is uniform inside reactant,but discontinuous at the boundary where there is a convection heat loss to the ambient at vessel boundary,the energy balance equation can put in the following form

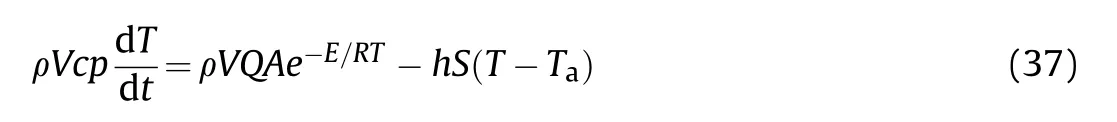
The dimensionless form of Eq.(37) can obtained as

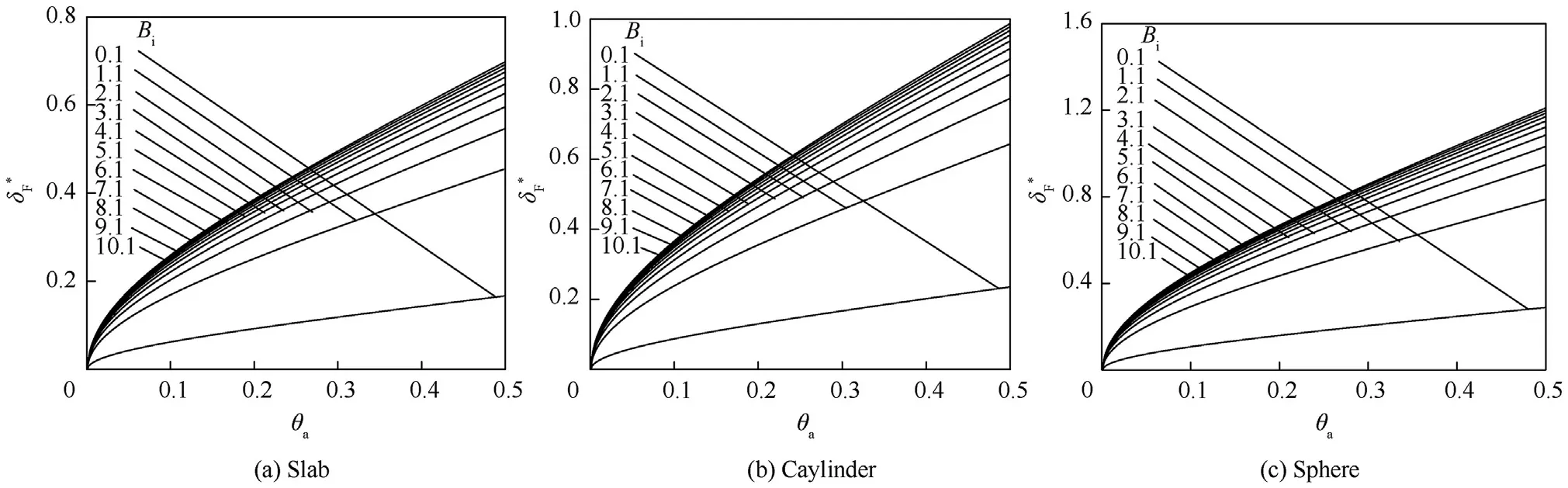
Fig.10.(a-c):vs θa for different Bi values for slab,cylinder and sphere.

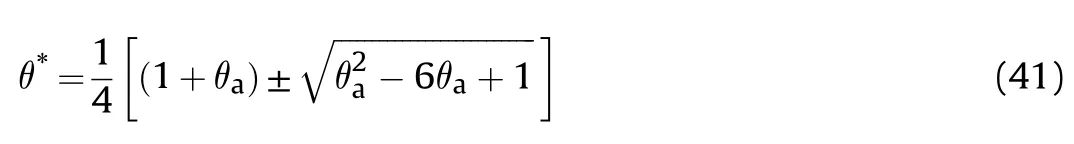
This equation is identical to Eq.(13)except that θis replaced θ.Also,this equation gives two region of solutions where θ＝0.171 for the first region as in Fig.3 and a second region where θ＝5.81 which cannot be practically possible.So,the Ψcan be obtained in the form

If the reactant gas mixture is contained in a vessel of constant volume V and surface area S where the effect of reactant consumption neglected,the overall energy equation for an isothermal reaction (uniform temperature)is

Fig.12.vs θa for constant pressure and constant volume explosions.

Fig.12 shows θvs θboth constant volume and constant pressure thermal explosion of gas mixture.It can see that the region of ignition (area under the curve) of constant volume are so narrower compared with that of constant pressure explosion.In addition,the transition point at which criticality disappears for constant pressure is almost 2/3 that value for constant volume.So,values of θwhich do not lead to ignition for constant pressure explosion leads to ignition in constant volume explosion.

Using the Frank-Kamenetskii approximation as shown above,Eq.(38) can put in the following form

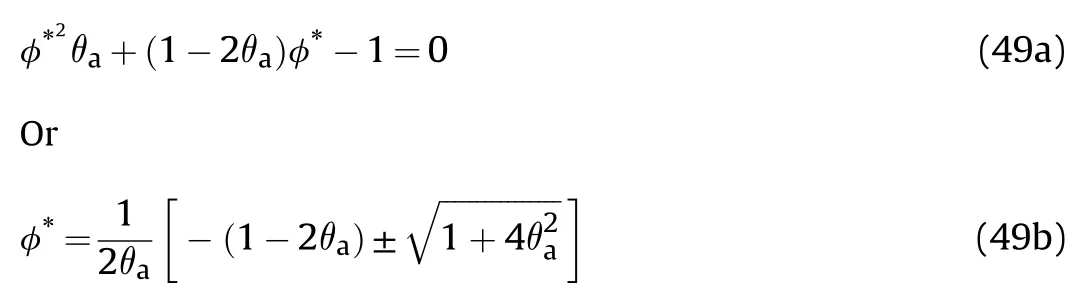
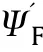
Fig.13.Showsvs φ*for different θa.

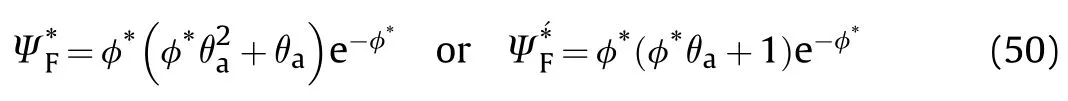
Using Eqs.(13) and (14),one can get

where the values 2,4,and 6 are for slab,cylinder,and sphere,respectively.However,for Frank-Kamenetskii critical parameter δ based on surface temperature are 0.88,2.0,and 3.32 for Bi→∞for solid material.

The Frank-Kamantskii δ can be rearranged to give a linear relationship for experimental determinations of the critical ambient temperatures for ignition (θ) of bodies of material of different shapes (δ*) and sizes (r) in the form

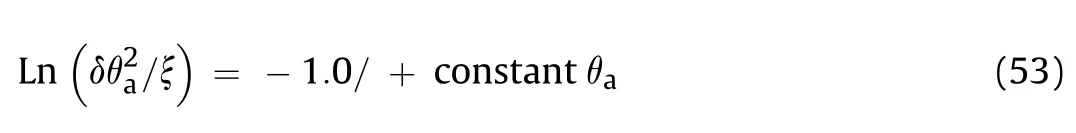
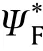
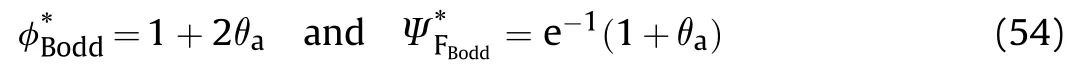
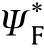
3.Conclusions

Approximate solutions for both the Frank-Kamantskii and Semenov models for the thermal explosion of gases at constant pressure were obtained.The solutions covers both the exact form of the Arrhenius reaction rate and the Frank-Kamenetskii approximation for that form.The critical characteristics parameters as critical maximum central ignition temperature,critical surface ignitions,transitional conditions and critical size were determined and the following conclusions can be derived as:

1 The solutions produce analytic expressions for both the critical ignition central temperature and the critical size.

2 The solutions are made quite general by considering two important cases: constant surface temperature and convection cooled boundary conditions,which are important in practical problems.

3 If the averages of the two solutions is used the precision of the results is improved.

4 The critical values of Frank-kamenetskii parameter δ for constant surface temperature overestimated than the values of convection cooled boundary conditions.

5 The critical thickness (size) of the vessel for slab ＜infinite cylinder ＜sphere and it depends on the central ignition temperature and ambient temperature.

7 The ambient temperature and the Biot number have a noticeable effect on the critical size (F.K.parameter δ),especially for the low Biot number.

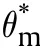
9 The transition condition at which criticality disappears are obtained for the two investigated cases for both Semenov and Frank-Kamenetskii models.

10 Validation of models with some exact solution and experimental results showed a fair satisfaction agreement.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.