One-bit splitting deceptive jamming against SAR

Bo Zho ,Lei Hung ,Bing Li ,* ,Shi-qi Liu ,Wei-min Bo ,b

a Guangdong Key Laboratory of Intelligent Information Processing,College of Information Engineering,Shenzhen University,Shenzhen,518060,China

b China Aerospace Science and Technology Corporation,Beijing,100048,China

Keywords:Synthetic aperture radar (SAR)1-Bit quantization Multi-false-target Single-frequency threshold

ABSTRACT One-bit quantization is a promising technique due to its performance retention and complexity reduction in a deceptive jammer against synthetic aperture radar (SAR).In this paper,the 1-bit quantization technology is utilized to agilely generate split false targets in the SAR imagery once the radar signal is intercepted,which reduces the complexity of the jammer significantly with guaranteed focusing quality.A single-frequency threshold is used to decompose harmonics incurred by the 1-bit quantization,and its parameters are adjusted through different pulse repetition intervals to provide steerable modulations.In this way,the SAR signal is split into coupled false scatterers during the 1-bit interception.By further deploying amplitude,time-delay,and Doppler frequency modulations on the 1-bit intercepted signal,the split false targets are created.The proposed approach is compared with different deceptive jamming methods to show its validity in effectiveness and cost,and numerical experiments are also presented for verification.

1.Introduction

Synthetic aperture radar (SAR) is an approach which provides continuous surveillance under various weather and illumination conditions,causing its wide application in civilian,especially in military reconnaissance.To prevent our targets from being detected by a hostile SAR,electronic countermeasures(ECM)against the SAR have been researched simultaneously as the SAR develops.

When an active jammer transmits electromagnetic waves to strive for the initiative in the ECM against SAR,a compromise has to be made between power consumption and computational complexity[1].A barrage jammer disturbs the SAR with high power noise which usually cannot be effectively accumulated through the SAR imaging algorithm.Submerged by the barrage jamming,the signal-to-noise (SNR) of the SAR imagery degrades.Thus it gets difficult for the hostile SAR to extract characteristics of the targets.The barrage jamming takes the advantage of low computational complexity.However,since the barrage jamming can hardly achieve a similar coherent processing gain to the SAR,a large amount of transmitting power is engaged in the barrage jammer,making it easy to expose.For a deceptive jammer,the situation reverses.The deceptive jammer imitates characteristics of the SAR echoes,enabling it to acquire high processing gain through SAR imaging,and thus much lower power is consumed than the barrage jamming.In this way,the understanding of the SAR imagery is misled by the false target imperceptibly,which is a more concealing and harmful countermeasure against SAR [2-5].Nevertheless,a large amount of calculations is necessary for deceptive jamming modulation.In another word,the advantage of the deceptive jammer in power consumption is at the cost of computational complexity.At a certain level of technology,the computational complexity is a bottleneck restricting the realization and practical application of the deceptive jamming.

To simplify the computation in the deceptive jammer with guaranteed quality of false targets,various efforts have been made.In Refs.[6-8],a deceptive jamming template is segmented into sub scenarios according to the depth of focus.Within each sub scenarios,modulation terms for different false scatterers are further divided into slow time-related and irrelevant parts.As the slow time irrelevant part can be handled offline,the real-time computational burden has been relieved by merely calculating the slow time related part.At the same time,the scenarios segmentation enables parallel modulation viable.Since the deceptive jamming can be considered as an inverse process to SAR imaging,a deceptive jamming scheme based on the inverse range-Doppler algorithm has been discussed in Ref.[9]to improve the efficiency of deceptive jamming.Similarly,Ref.[10]utilizes the inverse omega-K algorithm to reconcile focus capability and computational efficiency.By accomplishing the most time-consuming Stolt interpolation offline,the efficiency of deceptive jamming is guaranteed.Moreover,the Chirp-Z transform is further applied to tailor the algorithm for parallel computation.Refs.[11,12] calculates the frequency response of the jammer to perform deceptive jamming modulation in the frequency domain instead of time domain convolution.Ref.[13]employs slices of the intercepted SAR signal for deceptive jamming efficiency improvement at the cost of significant resolution loss.In addition,the problem of multiple false target generation remains unconsidered in these researches.As a result,computational complexity will be timed by the number of false targets to fulfill the multiple targets deceptive jamming task.

To tackle the multiple false target problem,a possible solution is cleaving the spectrum of intercepted signal into several parts.Such a spectrum cleaving is carried out by sub-Nyquist sampling during the interception of the LFM signal,which has been mostly discussed in the deceptive jamming against inverse SAR (ISAR)[14-16].When the LFM signal is intercepted by a rate which is much lower than the Nyquist rate,aliasing happens to the spectrum of the intercepted signal.The more times the spectrum aliases,the more false targets will be generated through a single modulation.However,the more significant resolution loss will be suffered by each target because of the bandwidth loss.Ref.[17]has discussed an implementation of the convolution involved in deceptive jamming modulation based on the sub-Nyquist approach,stating its advantage in realization.Moreover,the sub-Nyquist approach can also be extended to the slow time domain to create a matrix of false targets[18].Or in another way,polyphase coding is also able to induce multiple false targets in the azimuth domain with more easily controllable locations [19].Performance of the deceptive jamming based on sub-Nyquist sampling has been examined under the compressive sensing based imaging algorithm in Refs.[20-23],which qualitatively verifies the effectiveness of sub-Nyquist sampling in multiple false targets generation but ignores the quantitative degradation in bandwidth and resolution losses.

Instead of spectrum cleaving,a novel approach which splits the energy of the intercepted LFM signal is proposed in this paper to increase the efficiency of deceptive jamming modulation.The energy splitting is performed via 1-bit interception,which reduces the computational complexity significantly by quantizing each sample of the analog LFM signal into only 1-bit digital data.In this way,the signal processing involved in the deceptive jamming modulation can be significantly simplified.We have verified the effectiveness of deceptive jamming based on the 1-bit intercepted SAR signal in Ref.[24],and showed the remarkable complexity reduction brought by 1-bit signal processing in Ref.[25].It has been verified that the 1-bit signal can still be focused by the SAR imaging algorithm based on matched filter even without a sparsity premise,making the 1-bit deceptive jamming approach generally applicable.Additionally,a single-frequency threshold (SFT) has been introduced into 1-bit quantization for performance improvement in the 1-bit SAR imaging,and the abilities including spectrum shifting and energy reallocation of the SFT have been thoroughly studied in Refs.[26,27].As continuous research of 1-bit quantization,the SFT based 1-bit quantization is tailored for the deceptive jamming task,leading to halved computational complexity in addition to the 1-bit quantization.

The remainder of this paper is organized as follows.Section 2 tailors the SFT based 1-bit quantization model for splitting deceptive jamming.Employing time dependent frequency and phase,the SFT possesses the ability of spectrum splitting decomposition.In this way,part of the deceptive jamming modulation is forwarded to the interception module,which consumes very little computing resources.Deceptive jamming modulations inner and outer 1-bit interception are established to support the 1-bit splitting architecture.In Section 3,the principle error caused by jamming theory and practical error incurred by necessary approximation are analyzed.Numerical results are presented in Section 5 to verify the validity of the proposed method,and comparisons between different deceptive jamming methods are evaluated based on the cost-effectiveness analysis in Section 4.The conclusion is driven in Section 6.

2.Signal model

Due to its high resolution and high signal-to-noise gain,a linear frequency modulation (LFM) signal is usually adopted by a SAR,which can be formulated as

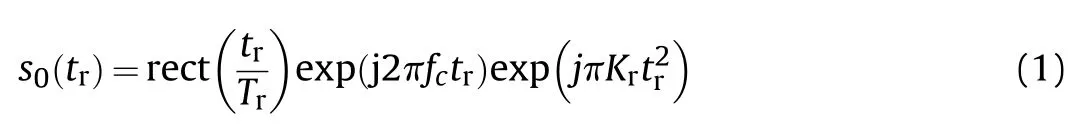
where rect（·）is the rectangular function denoting the envelope of the LFM pulse with a width,is the fast time,is the carrier frequency,andis the chirp rate.To achieve the purpose of the deceptive jamming,the primary task of the jammer is imitating the signal that the SAR transmits.Assume the deceptive jammer has been deployed at O（,）in the SAR imaging plane,and（）describes its distance from the SAR as a function of the slow time,then the LFM signal intercepted by the jammer is

where c is the propagation velocity of the electromagnetic wave.In a conventional deceptive jammer,the amplitude,time-delay,and Doppler frequency of Eq.(2)are modulated to create false targets in the SAR imagery.Such a process is performed on the digitized signal after the interception.Restricted by a state-of-the-art digital signal processor,the deceptive jammer has limited capabilities in handling a large false scene or multi-false targets jamming task with high efficiency,hindering its practical application.

In Ref.[24],a 1-bit interception scheme has been proposed for deceptive jamming,which verifies the feasibility of generating a false target in the SAR with only 1-bit data retained for each sample of the signal.As the 1-bit signal can be processed by logical operation instead of complex multiplication during the jamming modulation,the framework of the deceptive jammer is simplified significantly [25].However,the flipping between 1-bit samples incurs high order harmonics of the original LFM signal,and thus the SNR of the SAR imagery is degraded due to the defocusing characteristics of the harmonics.To relieve the performance degradation caused by 1-bit quantization,an SFT is introduced in Ref.[27].Although the cross modulation occurs between the SFT and the LFM signal,the spectrum shifting ability of the SFT,with properly designed parameters,is able to provide a purer spectrum within the passband of the matched filter.In this paper,the SFT based 1-bit quantization approach is modified for the deceptive jamming task to improve the jamming effectiveness with an extremely low complexity.Such a deceptive jamming scheme is illustrated in Fig.1.

Fig.1.Geometric model of 1-bit splitting deceptive jamming.

2.1.1-Bit splitting interception

Introducing the SFT complicates the spectrum of the intercepted SAR signal,however,it empowers the 1-bit quantizer to shift the spectrum of harmonics to meet different applications.For the deceptive jammer which tries to achieve high effectiveness with cost as low as possible,the SFT provides it a chance to increase the target number generated through a single round of deceptive jamming modulations at low complexity.For such a purpose,some harmonics should be retained rather than removed.The tailored 1-bit SFT quantizer for SAR signal interception can be written as

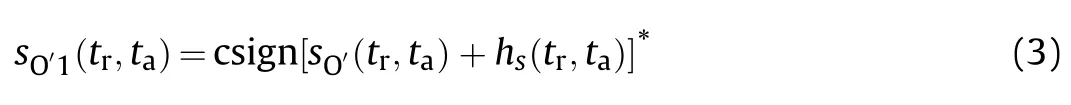
where（·）calculate the conjugation of a complex signal,csign（·）returns the sign of the complex samples,which is equivalent to sign［ℜ（·）]+j·sign［ℑ（·）],（,）is the SFT whose parameters vary in different pulse repetition intervals (PRI).The expression of（,）is

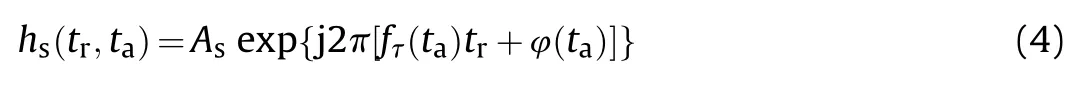
where Ais the amplitude of the SFT,（）and φ（）are the frequency and initial phase changing with the slow time.Denote the phase terms of the intercepted SAR signal and the SFT by φ and ψ,respectively.And then Eq.(5) is obtained according to Ref.[27].

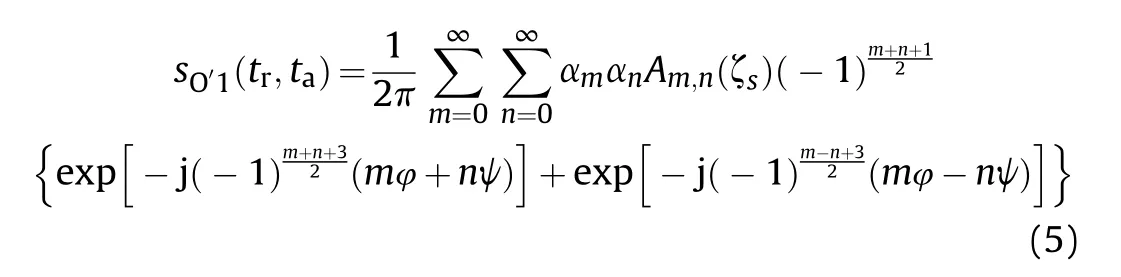
where ζ＝σ/is defined as the signal-to-threshold ratio (STR),α＝1 for＝＝0,and α＝2 whenoris greater than 0.The amplitude of the cross modulation components between theth order signal theth order SFT,say, Ahas been analyzed in Ref.[27] in detail and will not be repeated here.

The task that a deceptive jammer tries to fulfill is to generate false targets with high fidelity in the true SAR scene.The primary ingredient of high fidelity is that the false targets are well focused.To guarantee the focusing quality in the range domain,a candidate deceptive jamming component requires＝1 to ensure a matched chirp rate with the pulse compression filter employed by the SAR.According to the conclusion drawn in Ref.[27],a nonzero A（ζ）demands＝0,2,4,6,… for＝1.Asincreases, A（ζ）decreases for a fixed.Therefore,the component with＝1 and＝2 is selected for the deceptive jamming generation.Then（++3）/2 and（-+3）/2 are both odd,leading to the same chirp rate as the SAR signal in both exponential terms in Eq.(5).As a result,two false targets will be generated after matched filtering.Substituting＝1 and＝2 into Eq.(5),the deceptive jamming components can be written as

Eq.(6) reveals that the phase of the original SAR signal is split into two parts,which are further shifted by the positive and negative 2nd harmonic of the SFT.When the parameters of the SFT vary,the split spectra can be modulated according to the predesigned parameters,and thus the deceptive jamming involving coupled false scatterers is generated.Such a modulation is performed in analog during the 1-bit interception,saving much computational resource.

2.2.Inner splitting modulation

In the range domain,the jammer needs to adjust the slant range history of the intercepted SAR signal following the histories of the false scatterers,which can be illustrated in Fig.2(a).

The thick solid line in Fig.2(a) represents the range history of the intercepted SAR signal,which is equivalent to that of the scatterer O.Pand Pare true scatterers that the jammer tries to imitate,and their slant range histories are presented as dashed lines.Due to their different locations,each of them experiences offsets along the range axis and slow time axis in Fig.2,corresponding to the slant range and azimuth domain.For the deceptive jammer,however,it is impossible to completely duplicate the range histories of Pand Pbecause of the main lobe limitation[28].As a result,the deceptive jammer can work only when it is illuminated by the main lobe of the SAR.The range histories of the false scatterers that the deceptive jammer actually generates are denoted by the dotted lines in Fig.2(a).Notice that splitting the intercepted SAR signal in the slant range domain is not decomposing its envelope into two,but resolving its spectrum.Such a process,for a certainin the double dot dash line is further explained in Fig.2(b).

Fig.2.(a) Inner splitting modulation for slant range histories in the slow time domain.(b) time-frequency distribution of the intercepted signal in a certain instant.

By altering the frequency of the SFT for different PRIs,the characteristics of the true scatterers Pand Pare imitated in the slant range domain.However,it is only halfway done the inner splitting modulation.From a Doppler frequency perspective,Fig.3(a) reveals that the slant range histories of the deceptive jamming are not consistent with those of the true scatterers.Therefore,additional azimuth modulation is still necessary to achieve Fig.3(b).

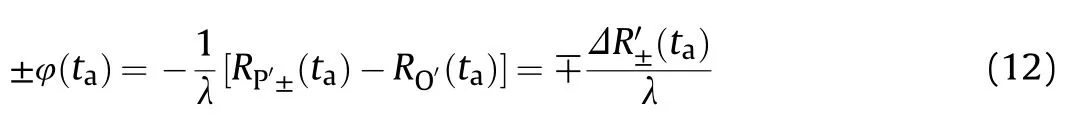
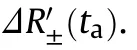
To sum up,the frequency and the phase of the SFT performs range and azimuth splitting,respectively.When the 1-bit interception is implemented based on such an SFT,the conventional modulation following the interception is not only simplified by dealing with 1-bit signal,but also generates dual false targets through one modulation,reducing the complexity of the deceptive jamming significantly.The conventional deceptive jamming modulation,which is named as outer modulation for the sake of distinction,is discussed as follows.

2.3.Outer modulation

In the azimuth domain,the last exponential term in Eq.(13)modulates the Doppler frequency as the inner azimuth modulation does,and will not be repeated here.

Fig.3.Split slant range histories in the Doppler frequency domain: (a) before azimuth inner modulation.(b) after azimuth inner modulation.

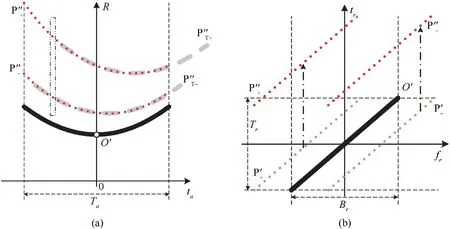
Fig.4.(a) Outer modulation for slant range histories in the slow time domain.(b) time-frequency distributions of the outer modulation.

3.Splitting modulation term selection and error analysis

A deceptive jamming algorithm may cause two kinds of errors,including theoretical errors which cannot be relieved because of the principle of deceptive jamming generation,and practical errors which can be reduced at the price of increased computational complexity.They are analyzed as follows.

3.1.Theoretical error

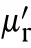
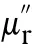
Processed by a SAR imaging algorithm,a two dimensional sinc function can be achieved for a true scatterer,which is denoted by

As the inner and outer modulation are performed sequentially,the bandwidth losses they caused accumulate,which not only degrade the amplitude but also broaden the width of the sinc functions.Taking the amplitude attenuation and mainlobe broadening into account,Eq.(17) is modified as

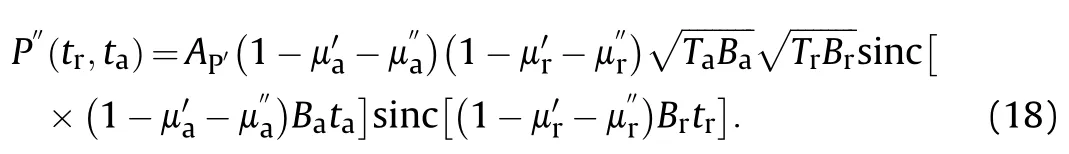
3.2.Practical error

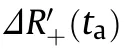
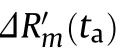
4.Cost-effectiveness analysis

The purpose of a jammer in ECM is achieving the greatest jamming effectiveness at the least cost,which can be described by a cost-effectiveness ratio (CER) minimization problem.The CER compares the relative costs and effects of different methods,which has been applied in the analysis on complex systems [29,30].It is introduced to synthetically evaluate the performance of the deceptive jamming methods in focusing quality,computational complexity,and false target number.In this section,analyses on the effectiveness and cost of a jammer are established to evaluate the CER of different deceptive jamming schemes.

Fig.6.Feasible region of inner modulation using （ta）.

4.1.Effectiveness analysis

In the deceptive jamming whose objective is interfering the hostile SAR unconsciously,the jamming effectiveness can be evaluated by the structural similarity (SSIM) between the false target and the true target sharing the same scattering characteristics.As the performance of deceptive jamming relies on the bandwidth loss during jamming modulation,results of deceptive jamming with different bandwidth losses in range and azimuth domains are simulated for a 50 m×50 m area.At the same time,true echoes of the same area are also simulated and imaged as the reference for SSIM evaluation.100 rounds simulations,in which amplitudes and phases of the scatterers change randomly following normal and uniform random distributions respectively,are performed and thus SSIM evaluation results versus bandwidth losses in Fig.7 are obtained.

In Fig.7,the SSIM suffers approximately linear degradation as the bandwidth loss occurs in a single dimension,and the degradation retards when two dimensional bandwidth lose simultaneously.Such a result reveals that the incoordinate bandwidth loss makes the deceptive jamming vulnerable to exposure.For different deceptive jamming methods,their bandwidth loss in each dimensionality can be quantitatively determined.The SSIM corresponding to the bandwidth losses according to Fig.7 is used as part of the effectiveness evaluation index.

Besides guaranteeing the fidelity of the false target,increasing the number of false targets can also improve the effectiveness of the deceptive jammer.Therefore,the effectiveness of the deceptive jamming is defined as a summation of SSIMs for all false targets.

4.2.Cost analysis

Computational complexity,which is the crucial factor imposing restrictions on the deployment of the deceptive jamming,is considered as the cost.On one hand,the computational complexity relies on the data amount that the deceptive jammer intercepts.Under the same performance,fewer data means fewer operations.On the other hand,the complexity of the deceptive jamming modulation is also the cost that the jammer needs to pay.The higher complexity of the jammer indicates more complicated and expensive hardware with lower efficiency.

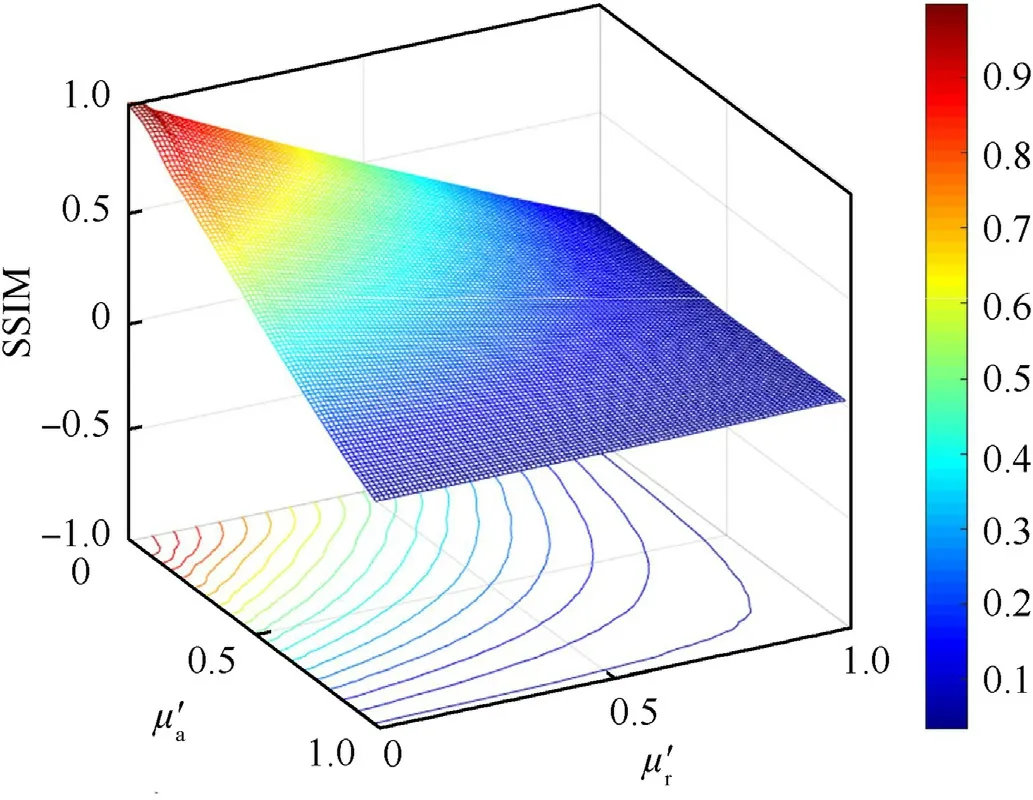
Fig.7.SSIM of deceptive jamming with bandwidth loss.

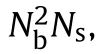
wheredenotes the number of false targets.For the conventional deceptive jammer,cost increases as the number of targets gets larger.Its bandwidth loss occurs only in the azimuth domain,and is controllable by constraining the location of the false target.Therefore,a bandwidth loss being less than 50% is assumed to guarantee the effectiveness of the deceptive jamming,leading to SSIM distributed in [0.5,1].The CER of the traditional deceptive jamming can be calculated by

Since the proposed 1-bit splitting deceptive jamming approach is able to obtain two false targets through a single modulation,its cost is timed by/2 rather than.Additionally,the quantization bit numberis reduced to 1.As a result,CER of the proposed algorithm is

In the sub-Nyquist based methods,an odd number of false targets are generated in the undersampled dimension.Defineandas the number of false targets generated in the range and azimuth domain,respectively.Then a matrix constructed by＝false targets are generated.If the template for deceptive jamming modulation further includes multiple false targets,targets in total,which is an integer multiple ofwill be finally achieved.andare calculated by

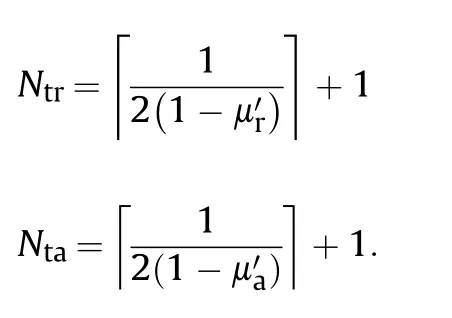
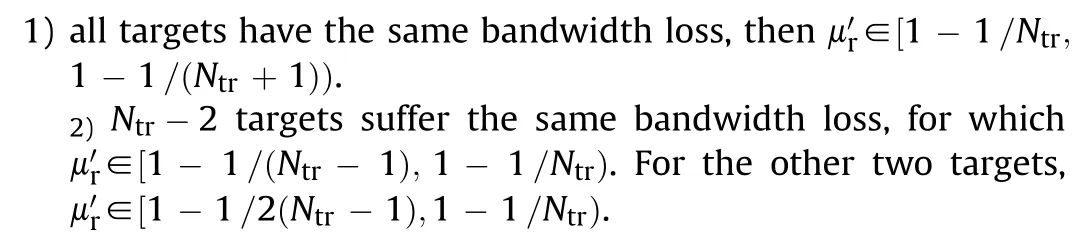
Situation is the same in the azimuth domain when sub-Nyquist sampling is applied.Then the SSIM of thus generated multiple false targets can be determined according to Fig.7 as well.As a result,the CER for sub-Nyquist approach can be calculated by

Notice that the Y-axis is presented by a logarithmic coordinate.The conventional deceptive jamming method is marked by ′+.It modulates a false target scatterer by scatterer.When the location of the false target is properly designed,the deceptive jamming is able to achieve the same quality of a true target.This leads to the lower CER bound of the conventional deceptive jammer,say η/η＝1.As the conventional deceptive jammer moves the false target in the azimuth domain,Doppler bandwidth loss occurs.As a result,the normalized CER is increased to about 4,which means that only a quarter of the effectiveness is retained with the same cost.As the false target numberincreases,the profit that the jammer gains increases synchronously,and the cost the jammer pays grows at the same time.Therefore,the CER remains unchanged withfor the conventional deceptive jamming approach as Fig.8 illustrates.The′□markers represent CERs of the sub-Nyquist approach applied in a single domain,which is denoted by η/η.Number of the false targets increases when the sampling frequency decreases,which also reduces the length of the intercepted signal,leading to lower computational complexity compared to a conventional jammer.These cause significant cost reduction to the jammer,reducing CERs although the quality of the false targets decreases due to the bandwidth loss.When the sub-Nyquist sampling is applied in both range and azimuth domain,η/ηdenoted by′○shows that only a specified amount of false targets can be generated,and the CER gets lower with the increased target number.The proposed 1-bit splitting deceptive jamming approach possesses the lowest CREs among different jamming methods as ′×s demonstrate,which indicates that the maximal effectiveness can be achieved with the least cost.Such an improvement in CRE is accomplished by the 1-bit quantization and splitting modulation.

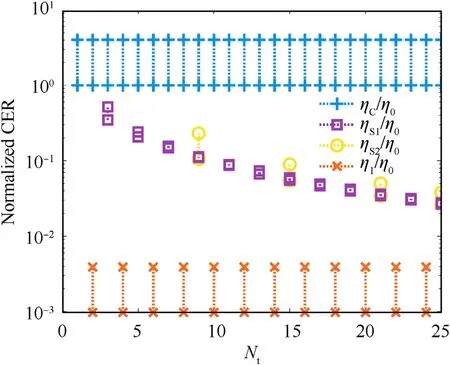
Fig.8.Normalized CER for different deceptive jamming methods versus number of false targets.

5.Numerical result

In the numerical simulation,an X-band SAR working in the strip-map mode with parameters given in Table 1 is examined.Deceptive jamming using scatterers is performed for quantitative analysis.Moreover,multiple false targets jamming results are also presented to verify the validity of the proposed 1-bit splitting jamming approach.

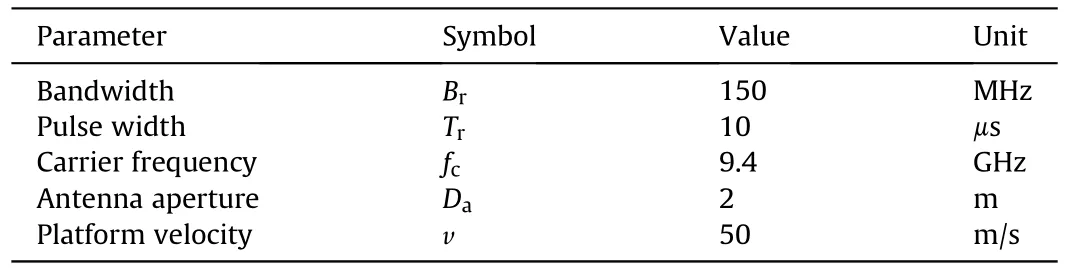
Table 1 Parameters of the SAR.

5.1.Scatterer deceptive jamming

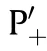
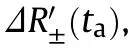
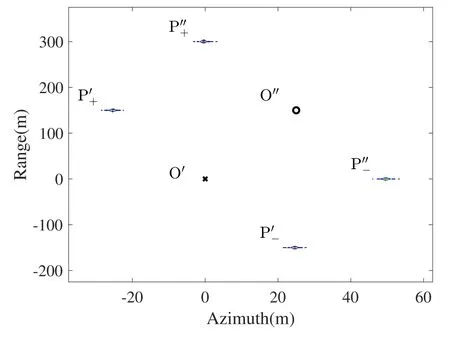
Fig.9.Deceptive jamming result of scatterers.

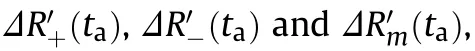
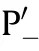
Fig.10.(a) True scatterer .(b) false scatterer .(c) false scatterer .(d) false scatterer .

Fig.11.(a) Range profile of .(b) azimuth profile of .

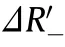
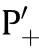
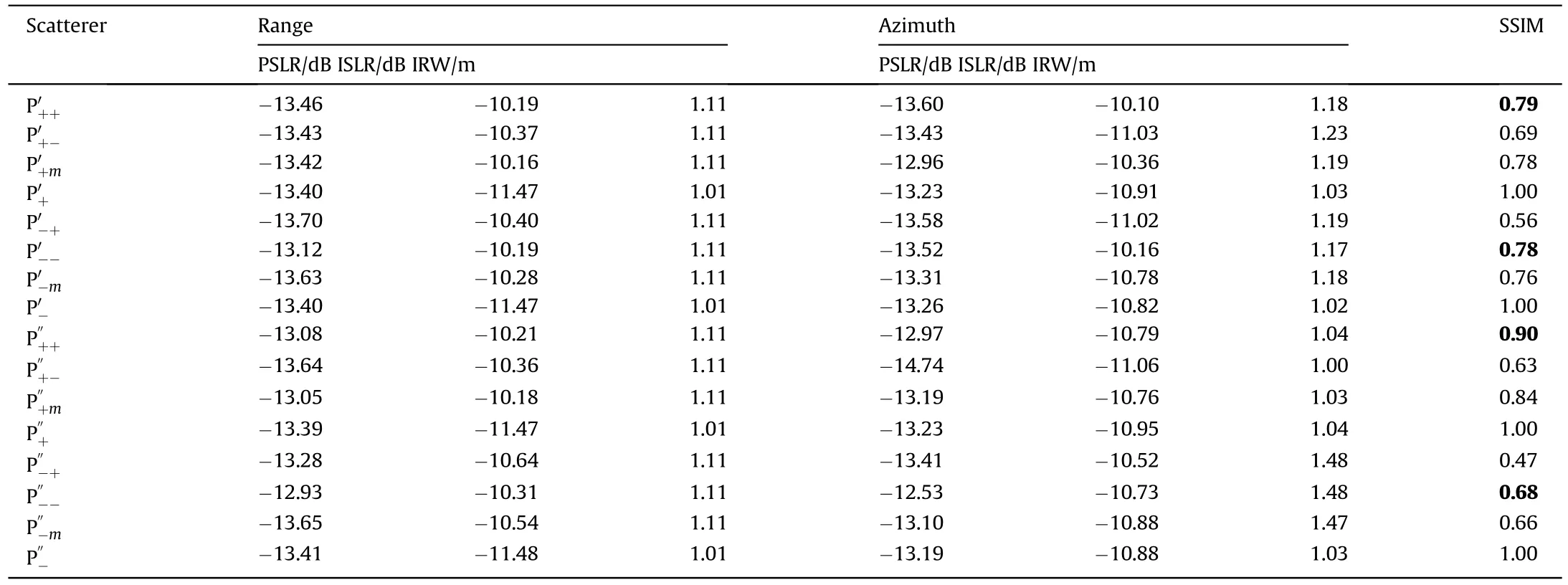
Table 2 Evaluation indexes of scatterer deceptive jamming.

Fig.12.(a) True scatterer .(b) false scatterer .(c) false scatterer .(d) false scatterer

Fig.13.(a) Range profile of .(b) azimuth profile of .

Fig.14.(a) True scatterer .(b) false scatterer .(c) false scatterer .(d) false scatterer .

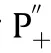
Fig.15.(a) Range profile of .(b) azimuth profile of .

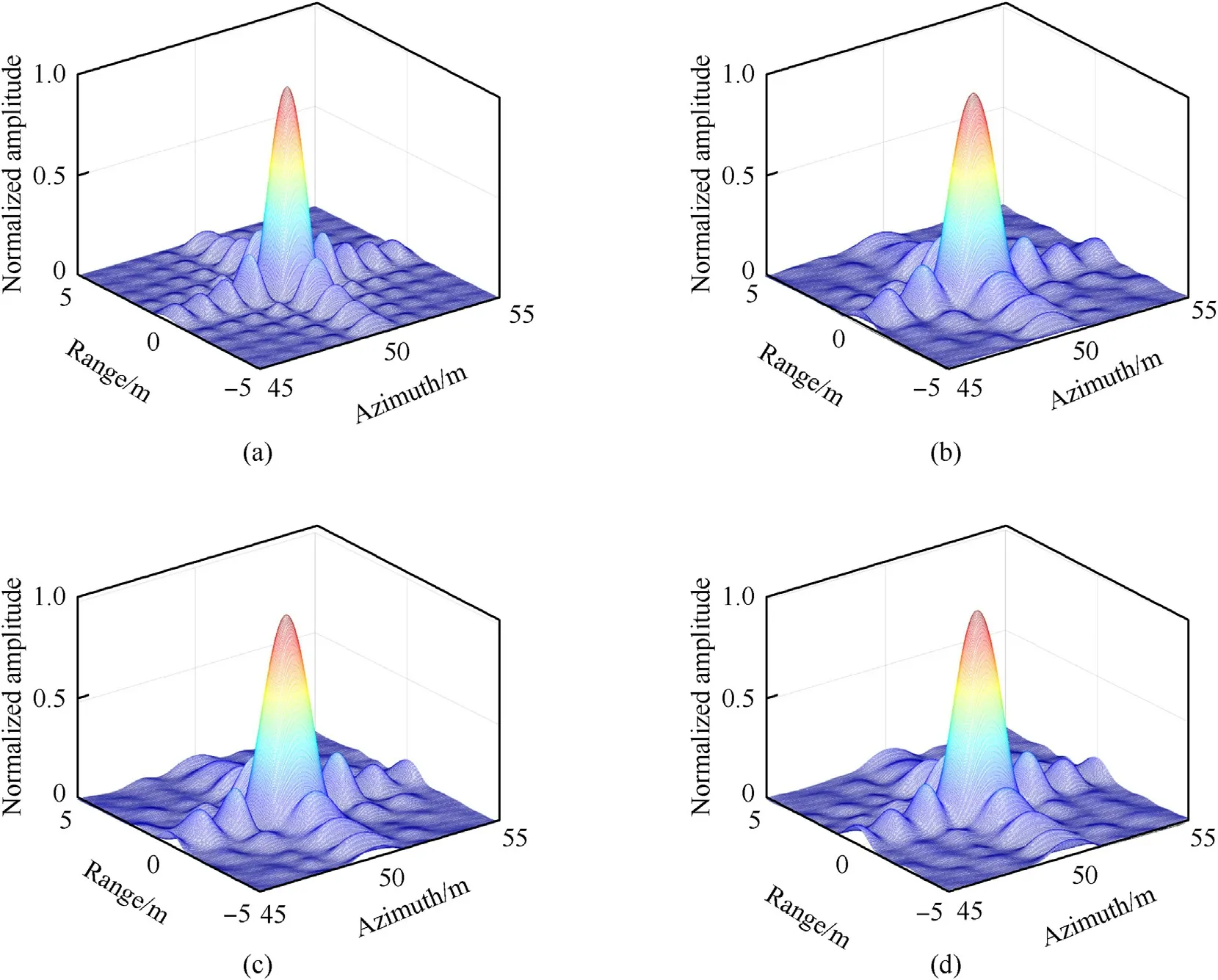
Fig.16.(a) True scatterer .(b) false scatterer .(c) false scatterer .(d) false scatterer.

5.2.Multi-target deceptive jamming based on sub-Nyquist sampling

For the purpose of comparison,the deceptive jamming approach based on sub-Nyquist sampling is simulated as well.As the sampling rate has been set to 1/3 of the Nyquist rate in both range and azimuth domains,a 3×3 false scatterer matrix is generated as Fig.18(b)shows.True scatterers arranged at the same locations are also presented in Fig.18(a).

Fig.17.(a) Range profile of .(b) azimuth profile of .

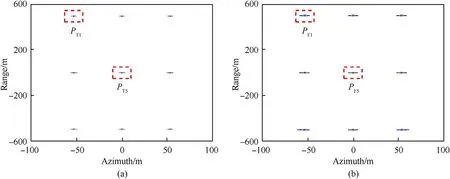
Fig.18.(a) Imagery of true scatterers.(b) imagery of false scatterers generated using sub-Nyquist approach.

The multiple false scatterers are achieved by actively introducing spectrum aliasing in the sub-Nyquist approach.As a result,significant bandwidth losses are suffered,which can be obviously seen from Fig.18.True scatterers P,P,and false scatterers P,Pare examined for quantitative evaluation.Their threedimensional details and sectional plots are given in Fig.19 and Fig.20,respectively.

As the sub-Nyquist approach divides the whole spectrum into pieces to generate multiple false targets,significant bandwidth loss occurs to each false scatterer and their sectional plots are broadened apparently.As Table 3 reveals,the IRWs of the false scatterers are about 2 times wider than that of the true scatterers,and SSIMs get as low as 0.3 around,which indicates significant performance degradation.

Table 3 Evaluation Indexes of false scatterers generated by the sub-Nyquist deceptive jamming approach.

5.3.Multi-target deceptive jamming

To verify the effectiveness of the proposed 1-bit deceptive jamming scheme under a practical circumstances,a real SAR scene measured by the Sandia-developed miniaturized SAR (MiniSAR)[31] is used for multi-target deceptive jamming simulation.The SAR imagery of the true scene is presented in Fig.21(a).

Imageries of targets such as BMP-2 infantry fighting vehicle,BTR-70 armoured transporter,and T-72 main battle tank collected as part of the DARPA/WL moving and stationary target acquisition and recognition (MSTAR) program are utilized as the template for outer modulation [32],which is illustrated in Fig.21(b).The deceptive jammer is deployed at the center,say（0,0）m in the imagery as the ′×in Fig.21(c).The inner modulation parameters Δand Δare set to 4 m and 8 m,respectively.The outer modulation parameters Δand Δare 30 m and 20 m as the ′○in Fig.21(c) shows.As a result,the false targets in Fig.21(b) are split and the deceptive jammed SAR imagery in Fig.21(c) is finally achieved.

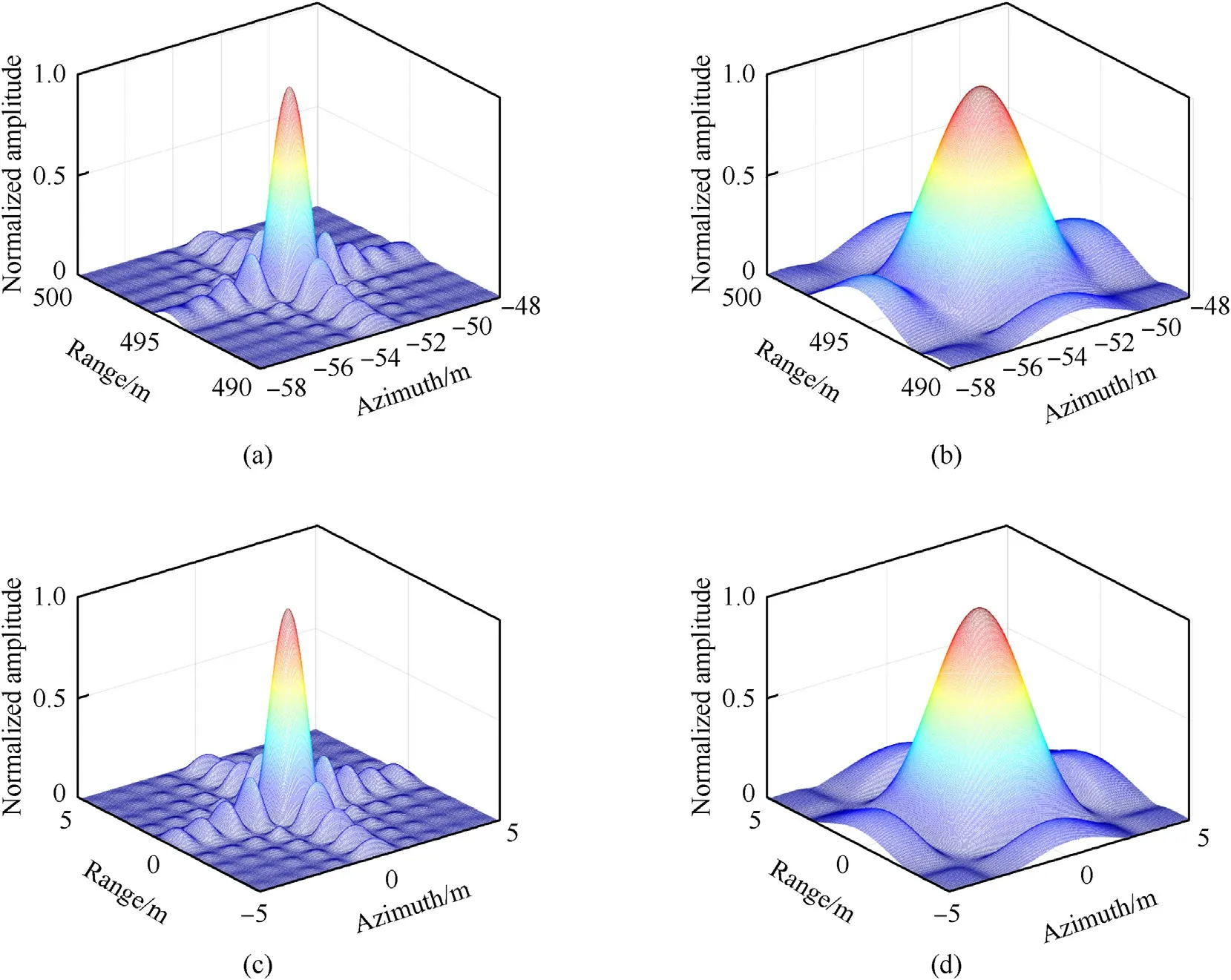
Fig.19.(a) True scatterer PT1.(b) false scatterer PF1.(c) true scatterer PT5.(d) false scatterer PF5.

Fig.20.(a) Range profile of PT1 and PF1.(b) azimuth profile of PT1 and PF1.(c) range profile of PT5 and PF5.(d) azimuth profile of PT5 and PF5.

Fig.21.(a) True SAR imagery.(b) false targets template.(c) deceptive jammed SAR imagery.

6.Conclusion

In this paper,the 1-bit quantization scheme has been modified to improve the CER of the deceptive jamming against SAR.The abilities of the SFT in harmonic decomposing and spectrum shifting are excavated to split the SAR signal during 1-bit interception.In this way,the task of deceptive jamming modulation is divided into inner and outer modulation.The inner modulation proceeds simultaneously with the 1-bit interception,which shifts the split false scatterers to the desired locations by adjusting parameters of the SFT in different PRIs.Sequentially,the outer modulation provides scattering characteristics and further location translations on the split scatterers to generate false targets.Analysis based on the CER has proved that the proposed 1-bit splitting deceptive jamming method is able to achieve much lower CER than the other methods,promoting its practical application.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

The authors would like to acknowledge National Natural Science Foundation of China (Grant No.61801297,62171293,U1713217,61971218,61601304,61801302,61701528),Natural Science Funding of Guangdong Province (Grant No.2017A030313336),Foundation of Shenzhen City (Grant No.JCYJ20170302142545828),and Shenzhen University(Grant No.2019119,2016057)to provide fund for conducting experiments.