Investigations on influence of rifle automatics system action on values of energetic efficiency coefficient of muzzle brakes
2022-10-17RadoslawTrebinskiZbigniewLeciejewskiJacekKijewskiDawidGozdzikDamianSzupienko
Radoslaw Trebinski,Zbigniew Leciejewski,Jacek Kijewski,Dawid Gozdzik,Damian Szupienko
Military University of Technology,Faculty of Mechatronics,Armament and Aerospace,ul.Gen.S.Kaliskiego 2,00-908,Warszawa,Poland
Keywords:Ballistics Muzzle brakes Automatic rifle Efficiency Recoil velocity
ABSTRACT The objective of the paper was to compare values of the muzzle brake efficiency coefficient for a rifle with active or inactive automatics systems.Special laboratory stand designed for investigating the recoil process was used.The motion of the rifle was detected by the use of the laser interferometer and the optical camera.The recoil velocity time courses were determined by smoothing and differentiation of experimental position records.The results of the experiments indicated that in the case of an active automatics system two values of the recoil velocity can be used for calculation of the energetic efficiency coefficient:the maximum recoil velocity and the final recoil velocity at the end of the automatics action cycle.The values of the coefficient,calculated using these two values of the recoil velocity,distinctly differ.However,it was shown that their values indicate the same relation between the efficiency of various muzzle brakes.The value of the efficiency coefficient,determined on the basis of the final recoil velocity value,is practically the same as that determined on the basis of the final recoil velocity value for the rifle with an inactive automatics system.
1.Introduction
The muzzle brake is a mechanical device attached to the muzzle of a rifle with the aim of reducing the recoil energy[1,2].The ratio of the difference of the recoil energy for a rifle without and with a muzzle brake to the recoil energy for a rifle without the brake is used as a measure of the muzzle brake efficiency.This measure will be referred to as the “energetic efficiency coefficient”.Another measure of the muzzle brake efficiency is proposed in Ref.[3].It is calculated as the ratio of the difference between recoil impulses for a rifle without and with a muzzle brake to the recoil impulse for a rifle without the brake in the period after the projectile leaves the muzzle.The results of investigations of the muzzle brakes efficiency were presented in Refs.[3-18].
The system of the rifle automatics makes use of part of the propellant gases energy for driving elements of the system.The gases exert a backward action,increasing the recoil energy.However,in the second part of the automatics cycle the bolt carrier moves forward,changing the recoil velocity.The energetic efficiency coefficient of a brake is determined as a rule on the basis of the recoil velocity value corresponding to the end of the automatics cycle.Such an approach does not take into account the transient process during the action of the automatics system.The question arises,does the action of the automatics system influence the value of the energetic efficiency coefficient of a brake?This question has not been addressed yet in the open literature.In order to obtain an answer to this question,a series of tests were performed using a laboratory stand for rifle recoil testing with an active or inactive rifle automatics system.The values of the energetic efficiency coefficient were compared for the two cases.Based on this comparison,conclusions concerning the influence of the action of the automatics system on the value of the energetic efficiency coefficient were formulated.
2.Method
2.1.Laboratory stand
The investigations on the influence of the rifle automatics system action on the determination of the effectiveness of muzzle brakes were performed using the laboratory stand shown in Fig.1([19]).A 5.56 mm automatic assault rifle was mounted on the stand.The automatics system elements were driven by propellant gases led away through a side vent in the barrel.By the use of fixing elements,the rifle was mounted on a carriage that rolled on the fences.The position of the rifle was recorded by the laser position sensor iLD-1750-750 (Micro-Epsilon Messtechnik,Germany).In tests with the active automatics system the motion of the rifle was additionally recorded by the high speed camera Phantom v12.The optical axis of its objective was perpendicular to the direction of motion of the rifle.
2.2.Muzzle brakes
The muzzle brakes used are presented in Fig.2.These are scaled research models of potential brakes intended for medium calibre anti-aircraft rifles.
The muzzle brakes 1,2 and 3 had an inner channel diverging towards the outlet (Fig.3).In each of 5 rows there were 4 vents placed on the perimeter at intervals of 90.The deflection angle φ values of the vents in brake 1 were:80in the first row,82in the remaining rows,in brake 2: 80in the first row,90in the remaining rows,in brake 3: 90in all rows.
Brakes 4,5,6 and 7 had an inner channel of the constant diameter 6.35 mm(Fig.4).Brakes 4 and 5 had 6 rows of 4 vents.The vents in a given row were placed on the perimeter with angles of 105and 75.The deflection angle values of the vents in brake 4 were:80in the first row,82in the remaining rows,and in brake 5: 90in all rows.
Brakes 6 and 7 had 6 rows of two vents of oval shape(Fig.5).The deflection angle values of the vents in brake 6 were:80in the first row,82in the remaining rows,and in brake 7: 90in all rows.
In the investigations 5.56 × 45 mm cartridges with a lead core produced by Mesko SA (Poland) were used.Their catalogue parameters are as follows: mass 11.2-12.1 g,length 56.6-57.3 mm,projectile mass 3.46-3.66 g,propellant mass 1.75 g,muzzle velocity 965 ± 12 m/s,maximum pressure 379 MPa (<400 MPa,>310 MPa).
For each variant (muzzle brake type,active or inactive automatics system),from 3 to 6 tests were performed.
2.3.Method of analysis
The results of the measurements gave the position of the rifle changing in time() in the form of sets of time values tand position values x.The experimental functions()were smoothed by the use of the Loess algorithm[20].Fig.6 presents the initial part of the experimental position course and the smoothed course.The smoothing eliminates effectively the experimental course disturbances.The velocity courses() are determined by the numerical differentiation of the smoothed position courses.Fig.7 presents the velocity course for the case of no brake.The velocity value increases to a maximum and then it rapidly decreases.From a certain moment of time,the velocity value decreases much more slowly.This part of the velocity course can be approximated by a linear function.It means that only the constant resistance force due to friction determines the velocity value.
In Fig.8 the velocity course determined by differentiating the() function is compared with the velocity course determined on the basis of the camera recording(as recorded and smoothed).The initial parts of the() courses agree well.Behind the maximum a difference between the both courses appears,which can be attributed to parallax error.
For calculation of the efficiency coefficient values,two velocity values were chosen: the maximum valueand the value just behind the peak of the velocity value.For determining the meanvalue,the results of the position measurements and of the camera recording were taken into account.Thevalues were calculated on the basis of the linear approximation of the velocity course behind the peak.
The presence of the initial peak of the velocity is a result of the automatics system action.In the case of an inactive automatics system,such a peak is not observed,so the choice of the velocity value is simpler.The position course is approximated by the quadratic function:


Fig.1.Laboratory stand for rifle recoil testing: 1 and 4 -elements fixing the rifle,2-5.56 mm assault rifle,3 -carriage,5 -fences,6 -laser position sensor.

Fig.2.Picture of muzzle brakes used.

Fig.3.Longitudinal section of muzzle brake 1.

Fig.4.Longitudinal section of brake 4.
In order to eliminate some initial disturbances,for the approximation the part of the() course in the time range[20-220] ms is chosen.In Fig.9 the experimental and the approximated course are compared.They converge for=15 ms.This value of time was chosen for calculation of the velocity value by the formula:

3.Results
The mean values ofandare given in Table 1.The sample's standard deviation divided by the square root of the number of test repetitions was chosen as the scatter measure.
The mean velocity values were used for calculation of the values of the energetic efficiency coefficient by the formula:

Subscript awb refers to tests with no brake,subscript ab refers to tests with a brake.The scatter measure of the coefficient value is calculated by the formula:
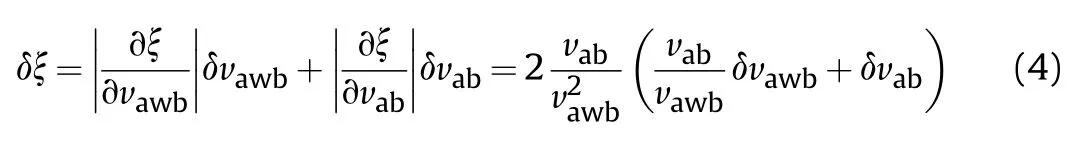
Symbols δandi δmean the scatter measures of the velocity values.
In Table 2,as well as in Figs.10 and 11,the values of the energetic efficiency coefficients ξand ξare compared.The values of ξare significantly lower than ξvalues.It shows that using the values of the recoil velocity at the end of the automatics cycle leads to an overestimation the energetic efficiency coefficient value.So,in investigations of newly designed muzzle brakes for automatic rifles the maximum recoil velocity during the automatics cycle should be taken into account.But for comparison of different designs of the muzzle brakes the value ξis sufficient.Despite differences between the ξand ξvalues,the relations between them for the various brakes are the same.It is interesting that the values of ξpractically coincide with the ξvalues.It means that a comparison of various brakes can be performed using the rifle with the inactive automatics system.As it was demonstrated in Section 2,the procedure for determining the recoil velocity is in this case much simpler.

Table 1 Mean velocity values vm,vk and vr.
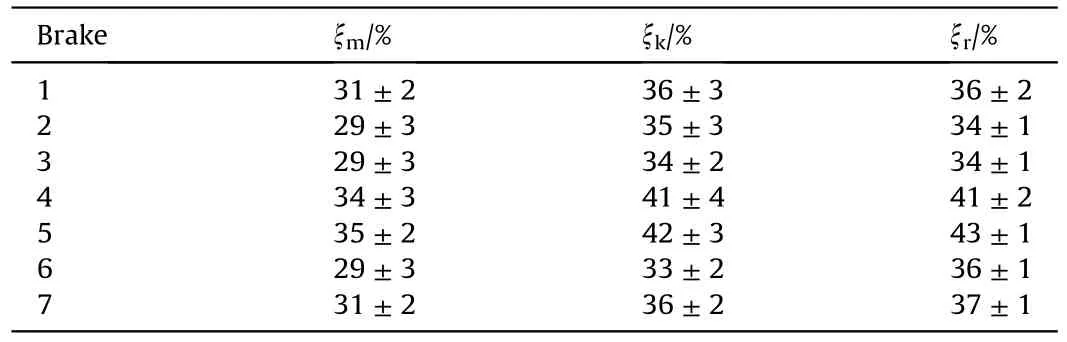
Table 2 Values of the energetic efficiency coefficients.
4.Discussion
Despite large differences between theandvalues,the values of ξand ξare practically the same.But they differ considerably from the ξvalues.In order to illustrate a reason for this difference,we refer to an illustrative model of the action of the automatics system.

Fig.5.Longitudinal section of brake 6.

Fig.6.Initial fragment of the position course: black line -experimental results,red line -smoothed course.
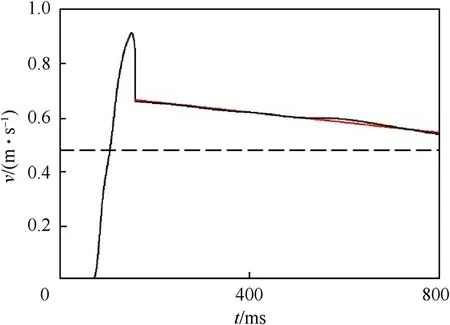
Fig.7.Velocity course:black line-result of differentiating the smoothed x(t)function,red line -linear approximation.
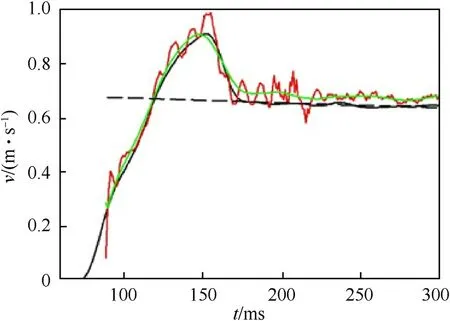
Fig.8.Velocity course:black line-result of differentiating the smoothed x(t)function,red line -result of camera recording,green line -smoothed result of camera recording,dashed line -linear approximation.
The used rifle was of the gas operated type with the short-stroke gas piston.During the shot,after the bullet passes the gas port in the barrel,an amount of the propellant gases is vented through the mentioned port into the gas chamber.The vented gases act on the front surface of the gas piston,which is connected to the operating rod.The gas piston with the operating rod drives the bolt carrier to the rear in the first period of its movement,providing enough energy to complete half of its operation cycle: unlocking the bolt,extracting and ejecting the shell casing,cocking the firing mechanism and impacting the recoil buffer.Then,affected by the recoil spring,the bolt carrier with the bolt returns to its starting position,locking the bolt at the end of the movement.When the bolt carrier impacts the front of the gun receiver,the set of weights located in the longitudinal channels in the bolt carrier body(weights are able to freely move inside channels) moves to the front of the bolt carrier and strike the front wall of the channels,limiting the possibility of the bolt carrier bouncing back after coming in a contact with the receiver.
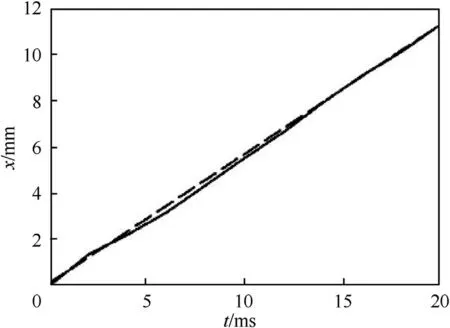
Fig.9.Initial fragment of the position course for inactive automatics system:solid line-experimental course,dashed line -approximation (1).
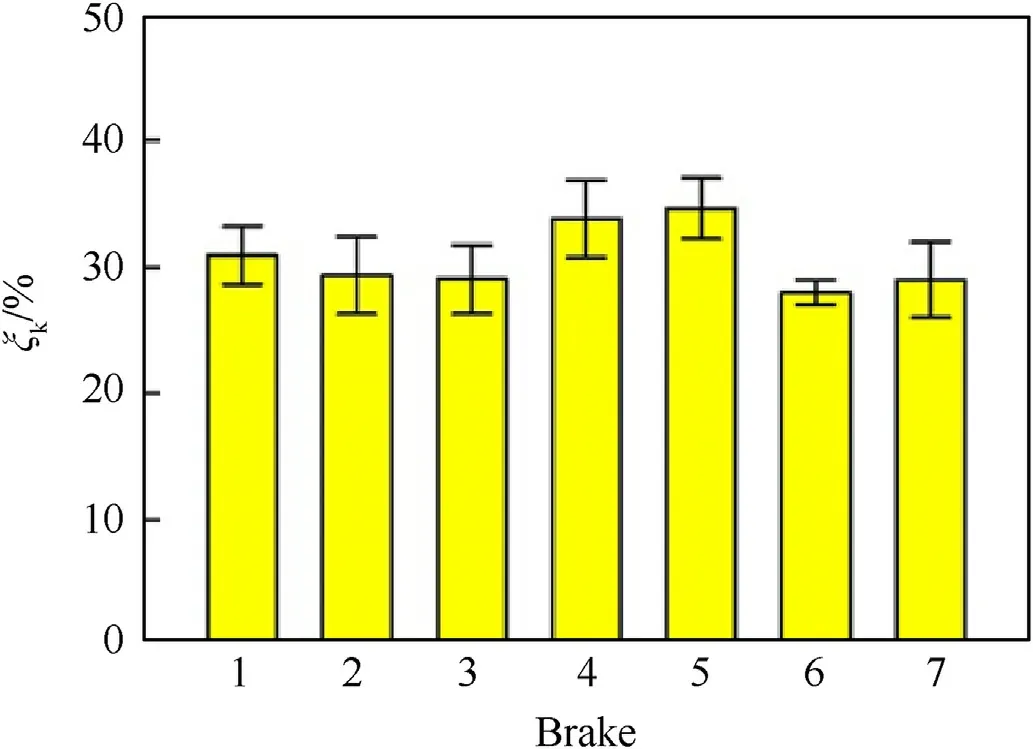
Fig.10.Comparison of ξm values.

Fig.11.Comparison of ξk values.
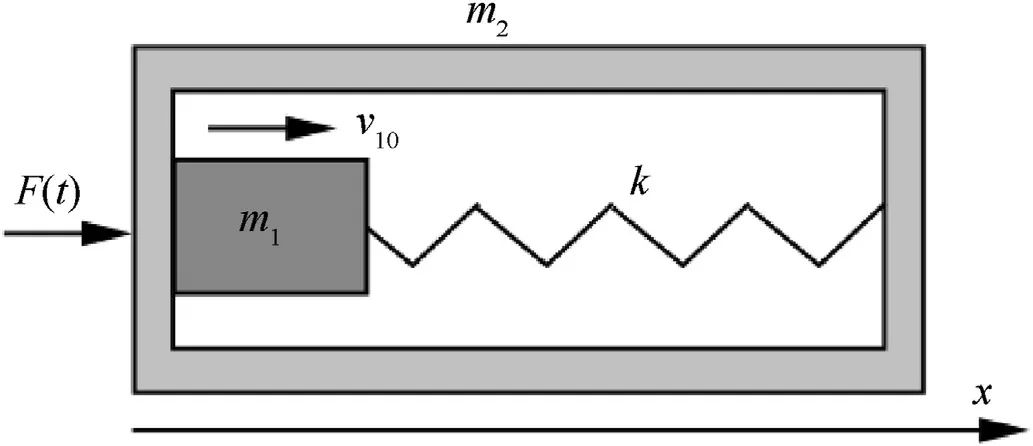
Fig.12.Scheme of the illustrative model.
From the point of view of our analysis,the most important features of the automatics system action are: the fast acceleration of the bolt carrier,the backward motion of the carrier hampered by the recoil spring,the forward motion of the carrier and stopping it at the moment of locking the bolt.Fig.12 presents a scheme of a system that behaves qualitatively as the modelled automatics system.The massmodels the inertia of the bolt carrier.We assume that due to the action of the gas piston it was accelerated to the velocity.The massmodels the inertia of the rest of the rifle.It is accelerated by the recoil force().The recoil spring has its constant.
In the rifle reference frame the massmoves as an harmonic oscillator.So,its velocity and displacement change in time as:

The equation of motion of the masshas the form:

Dividing both sides byand integrating,we obtain:

Making use of Eq.(6) we come to:
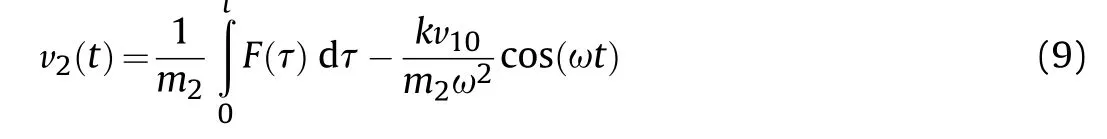
Making use of the expression for ω we can transform Eq.(9)to:
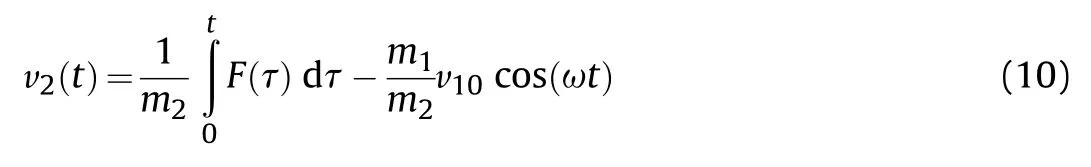
The velocity of the centre of the mass can be calculated as:

So,Eq.(10) can be written in the form:
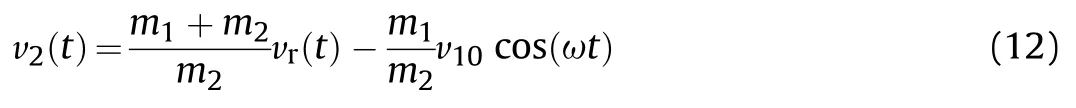
and finally:

In the first period the expression in the square bracket has a negative value.So,the velocity increases more slowly than in the case of the inactive automatics system.However,after a time the expression becomes positive and thevalue exceeds thevalue.At the moment,when the massstops,we have:

It can be assumed that at this moment the recoil force diminishes to zero andis equal to its final value.So we can express the velocities ofandas:
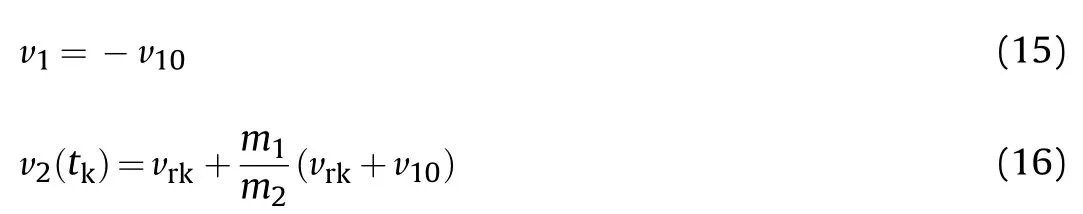
It results from Eq.(16)that thevalue may exceed considerably thevalue.It corresponds to.
We assume that from the moment the massreturns to its initial position both masses move with the same velocity,which can be determined from the momentum balance:

Making use of Eqs.(14) and (15),we come to:
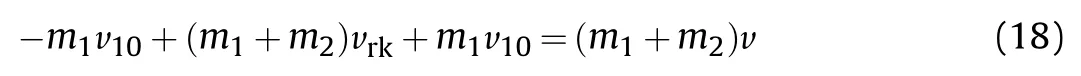
and finally to:

Although the model has only an illustrative character,it explains the convergence of the ξand ξvalues.The two values correspond to the motion of the whole mass of the rifle,while ξcorresponds to the motion of only a part of the rifle mass.
The differences between theandvalues indicate that the final recoil energy is lower for the rifle with the active automatics system.We must take into account that the friction influences the differences between theandvalues.The value ofwas determined when the rifle travelled a much shorter distance then the distance travelled to the moment when thevalue is determined.Making use of the slope of() behind the first peak,the friction coefficient value was estimated as equal to 0.01.Based on this value,we can assess that the friction is responsible for only a few percent of the difference between theandvalues.So,another reason for this difference should be identified.
We refer to the analysed model.The momentum balance Eq.(17) means that the collision of massesandis inelastic.So,part of the energy is dissipated.In the real system,the collision corresponds to the locking of the barrel.It is spread in time and corresponds to the transition fromto.Resistance forces during the locking are responsible for the mechanical energy losses.This explains the diminishing of the recoil energy.
5.Conclusions
The presented results of investigations and analysis enable us to formulate the following conclusions:
1.The estimation of the value of the energetic efficiency coefficient for rifles with active automatics system is ambiguous.The values calculated based on the maximum recoil velocity and the values calculated on the basis of the velocity value at the end of the cycle of the automatics system action differ considerably.
2.Despite differences between the ξand ξvalues,both can be used for comparison of the efficiency of muzzle brakes.
3.The value of the energetic efficiency coefficient calculated based on the velocity value at the end of the cycle of the automatics system action is very close to the value obtained for the rifle with an inactive automatics system.
4.The action of the automatics system temporarily increases the recoil velocity compared to the rifle with the inactive automatics system,but it reduces the final value of recoil energy.
5.The determined values of the energetic efficiency coefficient indicate that they are influenced by such factors as: the divergence angle of the brake channel,the deflection angle of the vents and the distribution of the vents on the perimeter.The influence of these factors will be analysed in a separate publication.
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
This work was supported by the National Research Centre[grant number DOBR/0046/R/ID1/2012/03].
杂志排行
Defence Technology的其它文章
- Establishment,simulation and verification of firepower safety control model
- Burning characteristics of high density foamed GAP/CL-20 propellants
- Cell-type continuous electromagnetic radiation system generating millimeter waves for active denial system applications
- Sandwich structure for enhancing the interface reaction of hexanitrohexaazaisowurtzitane and nanoporous carbon scaffolds film to improve the thermal decomposition performance
- Ablation characteristics of insulator under high-temperature gas dualpulse erosion
- Influence of shaped charge structure parameters on the formation of linear explosively formed projectiles
