短内腔激光器对光子储备池计算的优化*

赵彤 谢文丽 许俊伟 贾志伟†

1) (太原理工大学,新型传感器与智能控制教育部重点实验室,太原 030024)

2) (太原理工大学物理与光电工程学院,太原 030024)

随着高速信息时代的来临及信息量的爆炸式增长,对信息处理速度提出了更高的要求,光子储备池计算系统成为了解决方案之一.短光子寿命易于提升光子储备池计算系统的响应速度而有助于实现更高速率的信息处理.激光器内腔长度会影响光子寿命,同时还影响了激光器输出进入不同动力学状态时所需的相关参数值.因此,本文研究了不同内腔长度(120—900 µm)对基于分布式反馈激光器的储备池计算系统性能及相关参数空间的影响.结果表明,当内腔长度在120—171 µm 范围内,系统可低误差处理20 Gbps 速率的信息;内腔长度介于120—380 µm 之间时、较大的频率失谐及少量虚拟节点数(50),仍可使系统具有良好的预测效果;内腔长度较短时,反馈强度与注入强度组成的高性能参数空间可提高22%—40%.

1 引言

储备池计算系统是人工神经网络的一个重要分支,是为简化递归神经网络繁琐的训练每层权重而提出的改进方案[1-3],可以更好地解决人类社会迫切需要高效的信息处理方法的问题,成为快速信息处理的方案之一[4,5].它的输入权重和储备池内部权重是随机固定的,仅需训练输出权重,从而显著提高了系统的计算效率.同时,由于储备池中节点相互连接形成拓扑结构,使得系统具备记忆能力,因此对于处理与时间相关的动态任务具有独特优势[6,7].然而大量物理节点的连接使其在硬件实现上十分困难.

为克服上述硬件局限,Appeltant 等[8]提出了一种基于带有延时反馈环的单个非线性节点的储备池计算(reservoir computing,RC)系统,通过虚拟节点代替物理节点的方式极大简化了系统硬件结构.由于结构简单,延时型储备池计算已经基于电[9]、光电[10-13]、和光[14-21]的硬件实现.其中,半导体激光器凭借宽带宽、高速、低功耗等优势,迅速成为非线性节点的理想选择.

2013 年,Brunner 等[22]利用基于半导体激光二级管的RC 系统,将信息处理速率提升到1 Gbps以上.2015 年,Nguimdo 等[23]通过基于两种定向模式的半导体环形激光器的RC 系统实现了Santa-Fe 混沌时间序列预测任务和非线性信道均衡任务的并行处理.2018 年Vatin 等[24]提升了RC 系统的计算性能和记忆容量,这得益于具有高速偏振动力学的垂直腔面发射激光器.2019 年,Nguimdo 和Erneux[25]将非线性节点替换为量子级联激光器,未借助主激光器,将输入信息直接耦合到反馈光上,提高了使得储备池计算系统预测性能良好的参数范围.2021 年,Bogris 等[26]证明法布里-珀罗激光器在不同模式下采用不同的掩码信号可实现多种任务的并行处理.2020 年和2021 年,郭星星等[27]和黄于等[28]分别使用具有极短光子寿命的半导体纳米激光器和法诺激光器构建RC 系统实现了10 Gbps 速率的信息处理.

上述针对RC 系统信息处理速率提升方面的研究大多是更换系统中的非线性节点,然而作为最常见且使用最频繁的分布式反馈激光器(distributed feedback laser,DFB),众多研究者仅仅进行了普通商用DFB 产品的研究,对其内部参量变化引起的RC 性能提升并未过多关注.随着光子集成技术的发展,DFB的加工技术日益成熟,使得其尺寸在100 µm—1 mm 均可满足激光器的出光要求,随之而来的是激光器的光子寿命也会发生改变.由于短光子寿命会带来更快的动力学特性,因而可以在很大程度上提高RC 系统的响应速率.本文通过激光器内腔长度与光子寿命的关系,分析了内腔长度对激光器输出动力学特性的影响,及其变化对RC 系统高性能处理效果所需参数(反馈强度、注入强度、阈值电流等)取值范围的影响(即参数空间).结果表明在内腔长度不超过171 µm 时,光子寿命较小,实现了信息速率为20 Gbps的高质量处理;值得注意的是,当内腔长度由600 µm 降低到128 µm 时,RC 系统预测性能较好的参数空间大大提升,在执行Santa-Fe 混沌时间序列预测任务时,使得归一化均方误差(normalized mean square error,NMSE)小于0.01的注入强度参数范围提高22%左右,执行10 阶非线性自回归移动平均(10thorder nonlinear auto-regressive moving average,NARMA-10)任务时,使得NMSE ≤ 0.1的注入强度参数范围提高近40%.当内腔长度不超过514 µm、虚拟节点数为50 时,针对上述两种任务,系统均可实现高精度预测;且系统在内腔长度低于380 µm的范围内对频率失谐具有较强的鲁棒性.这对于系统的实用化发展具有重要的意义.

本文的结构安排如下: 第2 节介绍了RC 系统的结构和工作原理;第3 节是对理论模型的描述,其中包括RC 系统的理论模型、基准任务(Santa-Fe 混沌序列预测和NARMA-10 任务)及评判标准;第4 节通过上述两种基准任务对系统性能评估的结果,并对此进行了分析和讨论;第5 节是对全文的总结.

2 储备池计算系统

图1 所示为基于半导体激光器的延时型储备池计算系统的示意图,该系统中驱动激光器用作输入光源,输入信号与掩码信号Mask 相乘后,通过马赫-曾德尔调制器(MZM)将掩码后的信号采用时分复用的方式注入到带有延迟环的响应激光器中,经过延时回路后虚拟节点的瞬态响应Xi与输出层权重Wi线性叠加得到输出y.这里在延迟时间为τ的延迟回路中设置M个虚拟节点,相邻两节点间的间隔为θ,它们之间的关系是τ=M×θ.

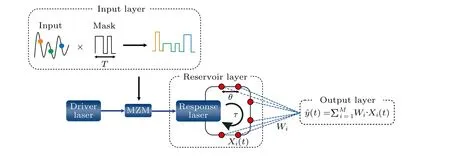
图1 基于半导体激光器的延时型储备池计算系统示意图Fig.1.Schematic diagram of a time-delayed reservoir computing system based on semiconductor laser.

输入层的功能是对输入信号进行预处理: 首先,对输入信号进行采样,并将每个采样点保持T的时间长度内恒定,然后将其与周期为T的掩码信号相乘后传输到储备池中.其中,掩码信号的作用等同于传统神经网络中的输入连接权重,在每个节点间隔θ内系统的输出被视为一个虚拟节点的瞬态响应状态.这里设置掩码信号周期T与延时时间τ相等,使得在整个延时环上完全充满对单个数据点的响应,因此本RC 系统的信息处理速率为1/τ.此外,有研究表明使用混沌信号作为掩码信号易引发响应激光器表现出更复杂的动力学特性,可有效提高RC 系统的性能[29],因此,在本系统中采用参考文献[30]中由光反馈半导体激光器产生的混沌时间序列作为掩码信号.

储备池的作用是将掩码后的输入信号映射到高维状态空间中,实现信号的非线性转换.输入信号经过τ时刻的延时环后,由虚拟节点的瞬态响应与输出权重线性叠加得到预测结果.这里通过将NMSE 最小化来进行对输出权重的训练.

3 理论模型

3.1 RC 系统模型

光子储备池计算系统中,最常用的响应激光器是DFB 激光器[22,31,32],该激光器的动力学特性通常使用速率方程(Lang-Kobayashi[33])分析,在储备池计算系统中光注入、光反馈作用下的DFB的速率方程描述如下[34]:

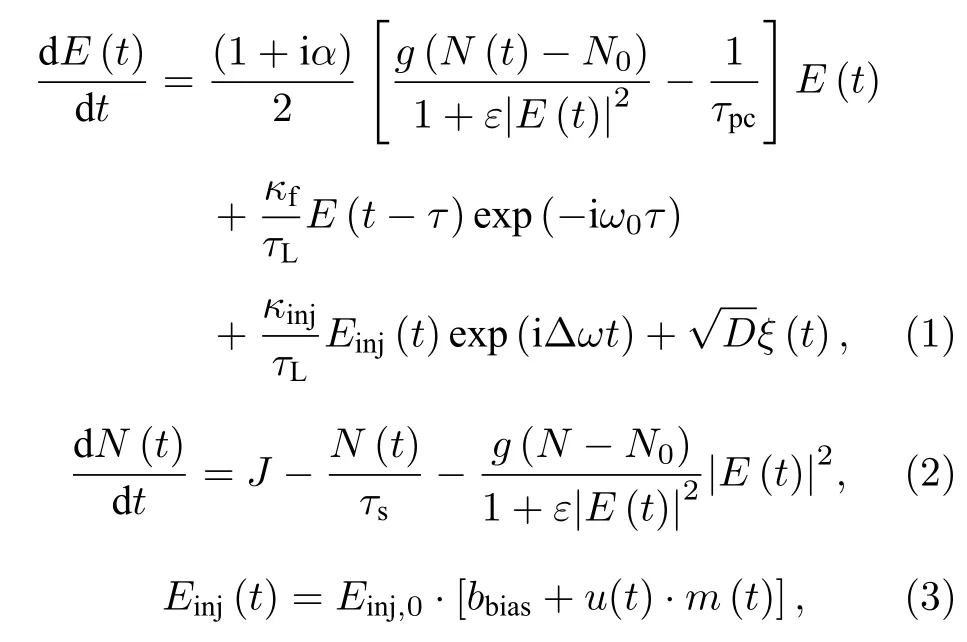
式中,E和N分别表示慢变电场的复振幅和平均载流子密度,kf是反馈强度,τL表示内腔往返时间,静态激光角频率ω0=2πc/λ0,τ表示反馈延时,kinj是注入强度,E(t -τ)和Einj(t)分别表示响应激光器的反馈光和注入光的电场,Δω=2π·Δν,Δν是驱动激光器和响应激光器之间的频率失谐,ξ(t)是高斯白噪声项,J是偏置电流,u(t)表示输入信号,m(t)表示掩码信号.这里采用四阶龙格库塔法来求解上述速率方程,其中步长为1 ps,仿真中用到的主要参数的含义及取值如表1 所列[31].

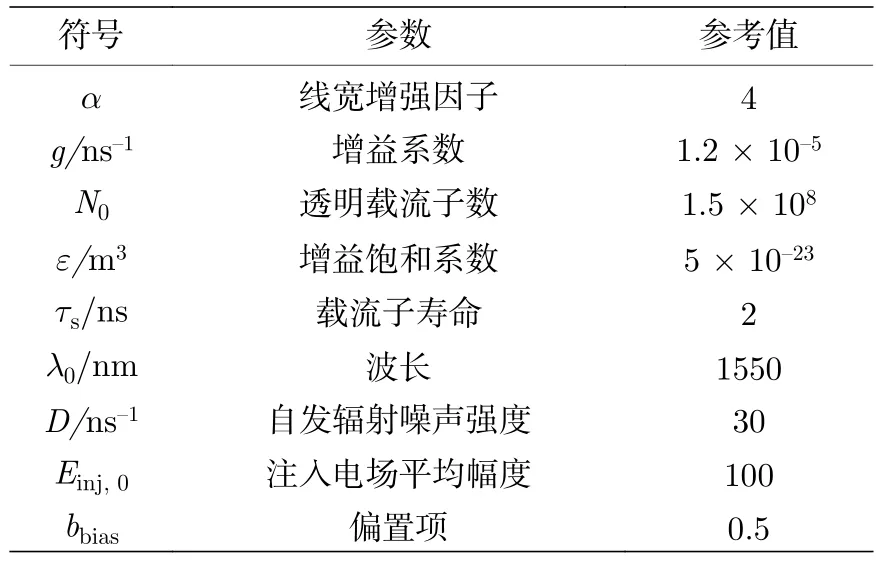
表1 数值模拟中DFB的部分参数Table 1.Partial parameters of DFB in numerical simulation.

3.2 基准任务及评估方法

本文采用了两种典型的基准任务—Santa-Fe 混沌时间序列任务和NARMA-10 任务,分析了不同内腔长度对系统性能的影响.

其中,Santa-Fe 混沌时间序列预测任务[35]中的数据是在混沌状态下运行的远红外激光的实验中记录所得,共包含9000 个点,本文选取其中的4000 个点,将前3000 个点作为训练集,后1000 个点作为测试集.该任务的目标是在下一个数据传入系统前,将该数据预测出,即一步预测.

NARMA-10 任务[36]的数据来源于(4)式中的模型.本文通过该系统获取4000 个点,其中的75%用于训练,余下25%用于测试.由于该任务复杂度较高,因此在处理时系统需具备更高的非线性和记忆能力.系统当前状态的输出不仅取决于当前时刻的输入信号,还依赖于10 步以前的输入和状态.

其中yk表示该系统在k时刻的输出,uk为区间[0,0.5]内均匀分布的随机序列.

本系统执行两种任务的效果均由NMSE 来评估,其定义如下[29]:

2.3 施工安全与效益的关系施工企业存在的目的是要创效益，不创效益的企业必然走向倒闭。然而效益是人创造的，不维护好人的安全何谈效益，人不安全谁去创效益?人是世界上第一可宝贵的，是社会生产力中最活跃的因素，而建筑施工安全就是要维护人的正当、正常、正确的生产劳动，进而创造效益。施工现场发生事故有直接损失和间接损失。直接损失往往是看得见的，而间接损失是一种潜在的常常是情绪化了的，不仅将影响企业创效益，而且由此又可能引发祸不单行的恶性循环。

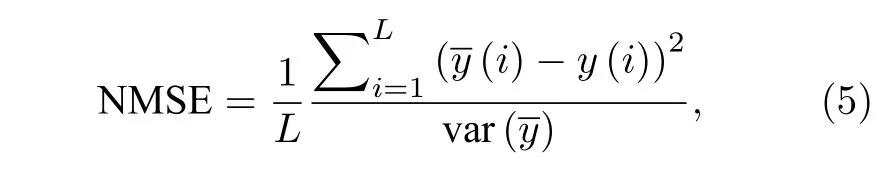
其中y¯ (i)是目标值,y(i)是预测值,L是测试集数据的总和,νar(y¯)表示目标值的方差.在Santa-Fe混沌时间序列预测任务中,当NMSE ≤ 0.01 时,认为该系统预测性能良好[37];在NARMA-10 任务中,综合以往对此任务的研究,这里以NMSE=0.1为分界线,小于0.1 时认为该系统处理性能较好.

4 仿真结果与分析

4.1 内腔长度对激光器输出的影响

激光器内腔长度l与内腔往返时间τL、光子寿命τpc、阈值载流子数Nth、阈值电流Ith的函数关系如下所示[33]:

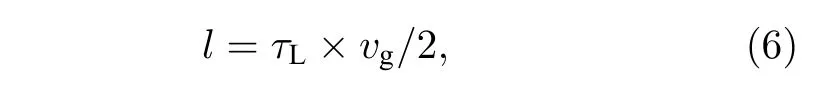
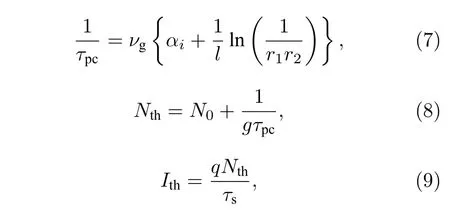
式中vg=c/ng为腔内的光速,其中,vg是群折射率,c是真空光速;αi表示内部损耗因子;r1,r2分别为激光器左右两端的反射率.仿真中,ng=3.5,c=3×108,αi=6 cm—1,r1=0.57,r2=0.57.

由(7)式可得,内腔长度与光子寿命呈线性关系.(8)式和(9)式表明,在内腔长度减小时,阈值载流子数也会相应下降,进而导致激光器阈值电流减小.在同等偏置电流下,该激光器的弛豫振荡频率提高,带宽增强,理论上可提高信息处理速率[38].

目前,随着半导体激光器工艺的进步,DFB的内腔长度范围的选择已可实现从100 µm 到1 mm.所以,接下来,在该范围内选取了不同的内腔长度,研究了相应情况下反馈光对DFB 输出动态特性的影响,结果如图2 所示.内腔长度分别选择128,300和600 µm,图中蓝色点和红色点分别代表该激光器在光反馈下输出时间序列波形中的最大值和最小值.图2(a)中霍普分岔点在κf=0.35%处,反馈强度小于0.35%时,蓝色点和红色点基本重合,此时激光器工作在稳定状态.随着反馈强度的增加,激光器输出逐渐进入倍周期、准周期和混沌状态.图2(b)和图2(c)的霍普分岔点分别为κf=0.95%和κf=2.05%,输出的动态特性规律与图2(a)相似.可以看出,随着内腔长度的变化,激光器输出处于各动态特性时所需反馈强度也不尽相同.

图2 DFB 激光器随着反馈强度变化的分岔图 (a) l=128 µm;(b) l=300 µm;(c) l=600 µm.I=1.05Ith,τ=0.2 nsFig.2.The bifurcation diagram of the DFB laser as a function of feedback strength κf: (a) l=128 µm;(b) l=300 µm;(c) l=600 µm.I=1.05Ith,τ=0.2 ns.

4.2 内腔长度对可处理信息速率的影响

信息处理速率是评判RC 系统处理能力的一个重要指标,因此本文分析了内腔长度对不同速率信息处理性能的影响.本节中所有分析都是基于固定虚拟节点数(M=50),改变节点间隔,进而实现信息处理速率的改变.为了更好地分析内腔长度的影响,响应激光器的其他相关参数分别设置为I=1.05Ith,κinj=0.5,κf=0.5%,Δv=20 GHz.

图3 所示为RC 系统执行Santa-Fe 混沌时间序列预测任务时,不同内腔长度下信息处理速率的相关结果,图中虚线为NMSE=0.01的情况.为了更加直观地观察内腔长度对信息处理速率影响的变化趋势,绘制了如图3(a)所示的曲线图.可以看出,随着待处理信息速率的提升,内腔长度对RC 系统处理性能的影响越来越明显.在内腔长度低于171 µm 时,信息处理速率在20 Gbps 下,系统依然可以表现出良好的性能,而一旦增加内腔长度,处理20 Gbps的速率信息的效果就显著下降.与之对应的是,在171 µm ≤l≤ 643 µm的范围内,该RC 系统处理速率分别为1,5 和10 Gbps的信息时,系统性能几乎不受内腔长度的影响,此时系统预测性能对内腔长度具有较强的鲁棒性.当内腔长度进一步提升时,系统处理10 Gbps 速率的信息时效果就会变差(NMSE ≥ 0.01),而1 和5 Gbps 信息处理速率的曲线依然基本重合,且两者在整个内腔长度范围内几乎无波动,由此说明该RC 系统在此分析条件下,处理5 Gbps 速率以下的信息受内腔长度的影响很小.

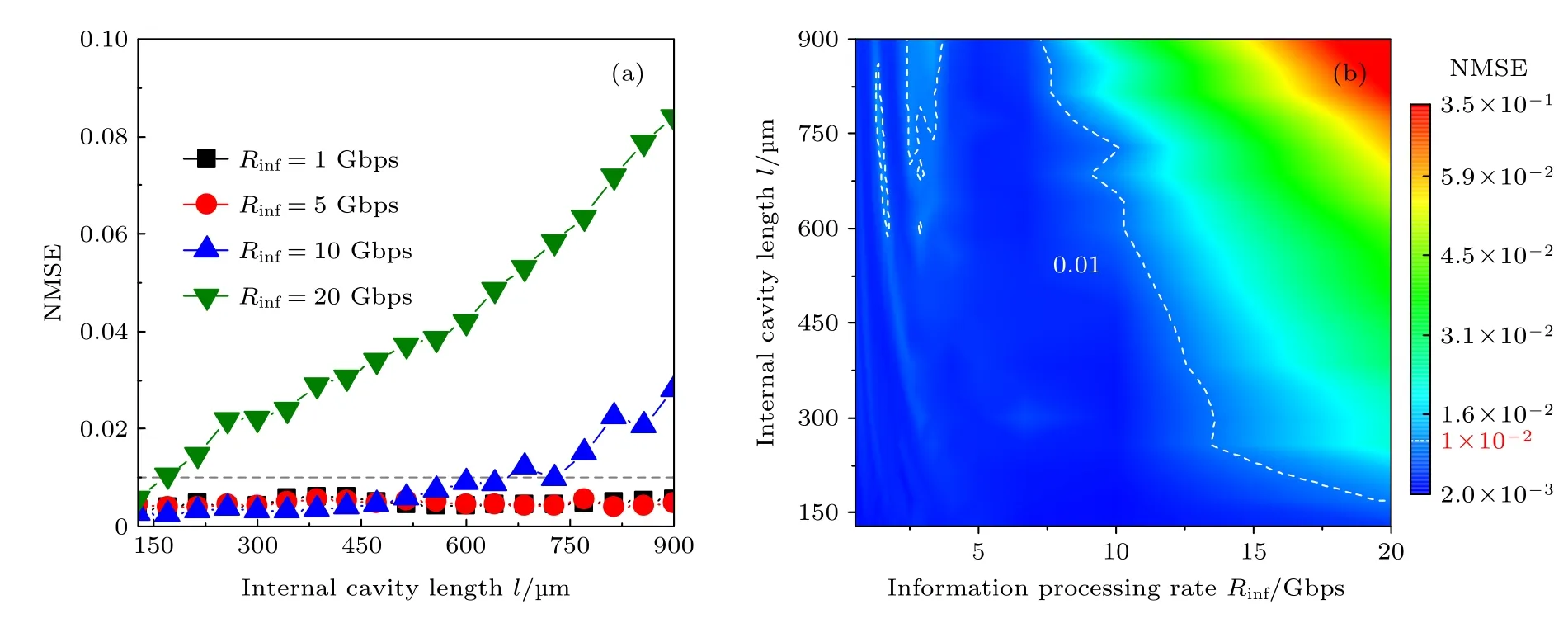
图3 基于Santa-Fe 混沌时间序列预测任务的(a) 不同信息处理速率下内腔长度对处理效果的影响,(b) 内腔长度与信息处理速率参数空间中NMSEs的二维图.I=1.05Ith,M=50,κinj=0.5,κf=0.5%,Δv=20 GHzFig.3.Based on Santa-Fe chaotic time series prediction task: (a) The influence of internal cavity length on processing effect under different information processing rate;(b) two dimensional maps of NMSEs in parameter space of internal cavity length and information processing rate. I=1.05Ith,M=50,κinj=0.5,κf=0.5%,Δv=20 GHz.

图4 是系统执行NARMA-10 任务的结果,其中虚线表示NMSE=0.1.首先,与图3 相比,在信息处理速率分别为5,10 和20 Gbps 时,均得到了相似的趋势.但在低速率(1 Gbps)下处理信息时,反而得到了较差的效果.这是由于NARMA-10 任务本身复杂度较高,执行该任务时对系统的非线性和记忆能力要求更高.在虚拟节点固定时,长外腔延时导致虚拟节点间隔过大,引起节点间耦合不充分对该任务的处理效果影响较大.从图4(a)可知,在内腔长度小于171 µm 时,系统依然可实现20 Gbps的信息处理速率.随着内腔长度的增加,同一速率下的NMSE 不断增加.当内腔长度增大到471 µm 后,可实现NMSE ≤ 0.1 条件的信息处理速率大幅度下降,无法再达到5 Gbps.进一步增加其至771 µm之后,4 种信息速率下系统都无法满足高性能预测.但是总体上在整个内腔长度范围内,信息处理速率为5 和10 Gbps 时受到的影响较小.

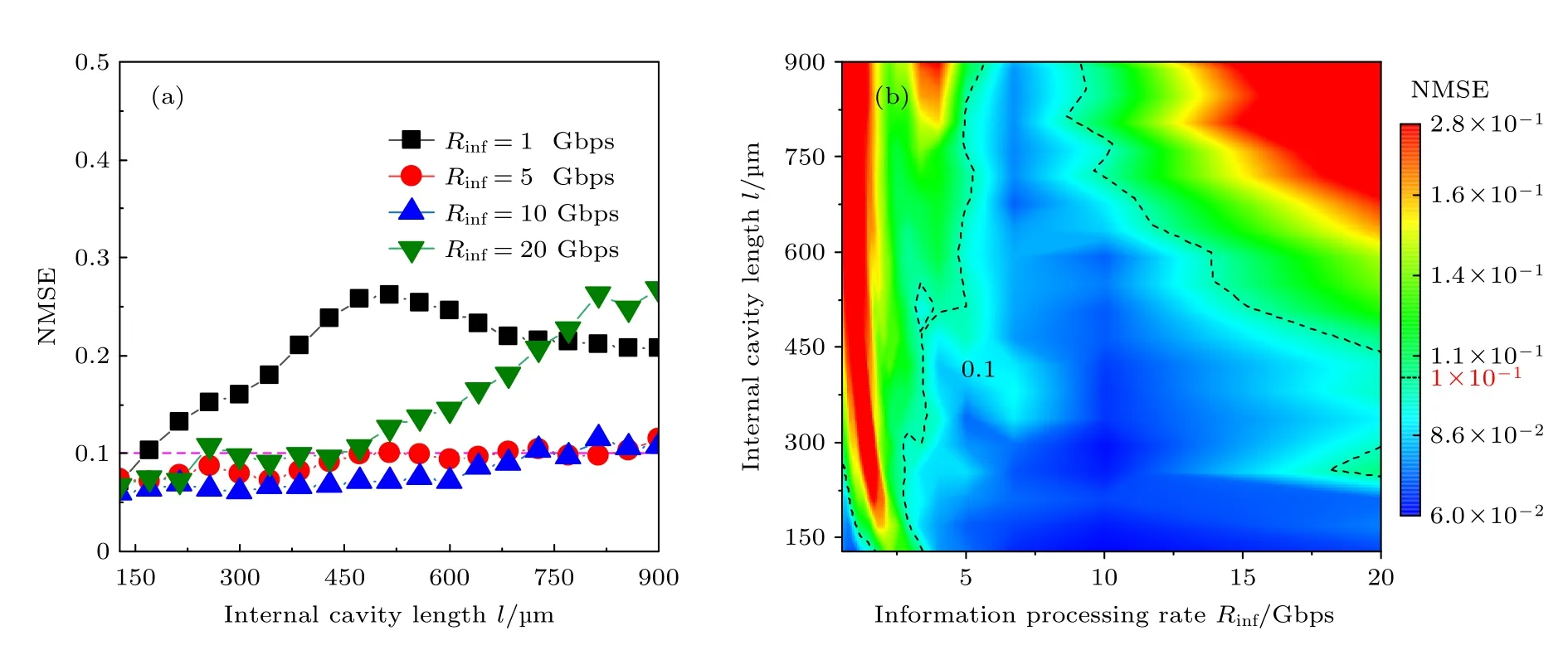
图4 基于NARMA-10 任务的(a) 不同信息处理速率下内腔长度对处理效果的影响,(b) 在内腔长度与信息处理速率参数空间中NMSEs的二维图.I=1.05Ith,M=50,κinj=0.5,κf=0.5%,Δv=20 GHzFig.4.Based on NARMA-10 task: (a) The influence of internal cavity length on processing effect under different information processing rate;(b) two dimensional maps of NMSEs in parameter space of internal cavity length and information processing rate.I=1.05Ith,M=50,κinj=0.5,κf=0.5%,Δv=20 GHz.

图4(b)为内腔长度与信息处理速率参数空间内NMSEs的二维图.与图4(a)相比,可从整体看到一些特殊的趋势,在Rinf≤ 2.5 Gbps 时,在整个内腔长度范围内系统表现较差.提高信息处理速率后,在2.5 Gbps ≤Rinf≤ 5 Gbps 区间内,使得预测性能表现良好的内腔长度范围增加.当5 Gbps ≤Rinf≤ 10 Gbps 时,NMSE ≤ 0.1 几乎不受内腔长度的限制,此时具有较强的鲁棒性.信息处理速率进一步提升,NMSE 低于0.1的区域面积大大减小.从图3 和图4 均可可看出,短内腔长度可有效提高系统的信息处理速率.

4.3 内腔长度对最优参数范围的影响

在延时型RC 系统中,虚拟节点数M决定了系统的维度,当M过小时会导致模型维度较低,难以构建复杂任务的模型.但增加M的前提是有足够长的外腔延时,这意味着要牺牲信息处理速率,因此在接下来的研究中加入了不同内腔长度下M的分析.同时,由于内腔长度改变会引起激光器输出不同动力学特性的条件发生变化,如外部频率失谐、注入强度、反馈强度等参数的范围,因此,下面分析内腔长度对上述参数范围的影响.此外,根据以往的研究经验,当偏置电流在阈值附近时,系统效果较好[22],所以接下来将偏置电流设置为阈值电流的1.05 倍,且外腔延时固定为0.2 ns.

1)虚拟节点数的取值范围

图5 是不同虚拟节点数的情况下,RC 系统处理两种任务时NMSE 受内腔长度的影响结果.其中,受噪声的影响,每次处理结果会有一定的差异,图5 中误差棒的长短表示5 次运行后求得的标准差的大小.该系统执行Santa-Fe 混沌时间序列预测任务的情况如图5(a)所示,其中虚线代表NMSE=0.01.从图5(a)可得,在虚拟节点数为20 时,NMSE在所考虑的内腔长度范围内都位于虚线上方,即系统预测性能较差.这同样是由于在延时时间固定时,虚拟节点数较少,导致节点间隔过大,进而使得节点间耦合不充分造成系统性能下降[8].随着虚拟节点数增大到50,系统的预测性能有明显的提升,在内腔长度研究范围内,NMSE 都在虚线以下,且NMSE的误差很小.进一步将其增加到100,200时,三条曲线基本重合,相比于M=50 时,NMSE降低效果并不明显.且M=100 时,在l≤ 514 µm的范围内,预测误差会高于内腔长度l≥ 514 µm的部分.而虚拟节点数增加到200 时,在大于514 µm的区间内有较大的误差棒,这意味着长内腔长度下系统受噪声影响较大.

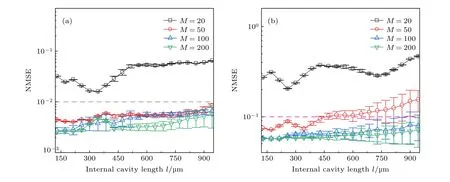
图5 不同虚拟节点数下内腔长度对NMSE的影响 (a) Santa-Fe 混沌时间序列预测任务;(b) NARMA-10 任务.I=1.05 Ith,M=50,κinj=0.5,κf=1%,Δv=20 GHzFig.5.The influence of internal cavity length on NMSE under different numbers of virtual nodes: (a) Santa-Fe chaotic time series prediction task;(b) NARMA-10 task.I=1.05 Ith,M=50,κinj=0.5,κf=1%,Δv=20 GHz.

执行NARMA-10 任务时的效果如图5(b)所示,获得了与图5(a)相似的趋势.在虚拟节点数为20的情况下系统效果依然较差,且误差棒的长度几乎为零.但是在虚拟节点数为M=50 与M=100 时,两者有明显的差距.这是因为该任务需要较高的非线性和记忆能力,在虚拟节点数较少时难以满足此要求.虚拟节点数进一步增大到200 时,基本与M=100 时的曲线重合.与此同时,随着内腔长度的增加,误差棒变得越来越明显,系统此时受噪声影响较大.从图5 总体上看,随着内腔长度的增加,NMSE 大体上呈现上升趋势,这意味着小的内腔长度有助于获得较好的预测性能.综合考虑速率和预测性能,在接下来的分析中将虚拟节点数设置为50.

2)频率失谐范围

图6 研究了内腔长度在不同频率失谐下对系统性能的影响.图6(a)是基于Santa-Fe 混沌时间序列预测任务的效果,虚线表示NMSE=0.01.图6(a)中当—40 GHz ≤ Δv≤ —20 GHz 时,该系统仅在很小的内腔长度范围(l≤ 214 µm)内表现良好.随着频率失谐从—20 GHz 变化到40 GHz 时,在l≤ 450 µm 范围内,NMSE 在2×10—3—8×10—3之间浮动,变化幅度极小,表明此时系统独立于频率失谐,具有较强的鲁棒性.频率失谐范围缩小至10—25 GHz 时,在整个内腔长度范围内均处于NMSE小于0.01的区域.随着频率失谐增大到40 GHz,在内腔长度大于450 µm 时,预测性能发生明显的降低.

图6(b)所示为NARMA-10 任务的执行效果,实线表示NMSE=0.1的情况,获得了与Santa-Fe 混沌序列预测任务相似的效果,但是效果上稍微有些下降.图6(b)中当频率失谐小于—30 GHz时,几乎在整个内腔长度范围内系统表现良好.随着频率失谐的增大,当—30 GHz ≤ Δv≤ 40 GHz,在l≤ 380 µm 时,NMSE 几乎都在0.1 以下,且系统预测性能基本上不受频率失谐的影响.随着内腔长度逐渐增大,预测性能明显下降.从图6 整体来看,频率失谐为20 GHz 时,对于两种任务,系统性能变化都较小,将Δv固定为20 GHz,便于后续使用单一变量原则来分析系统对注入强度或反馈强度的依赖性.

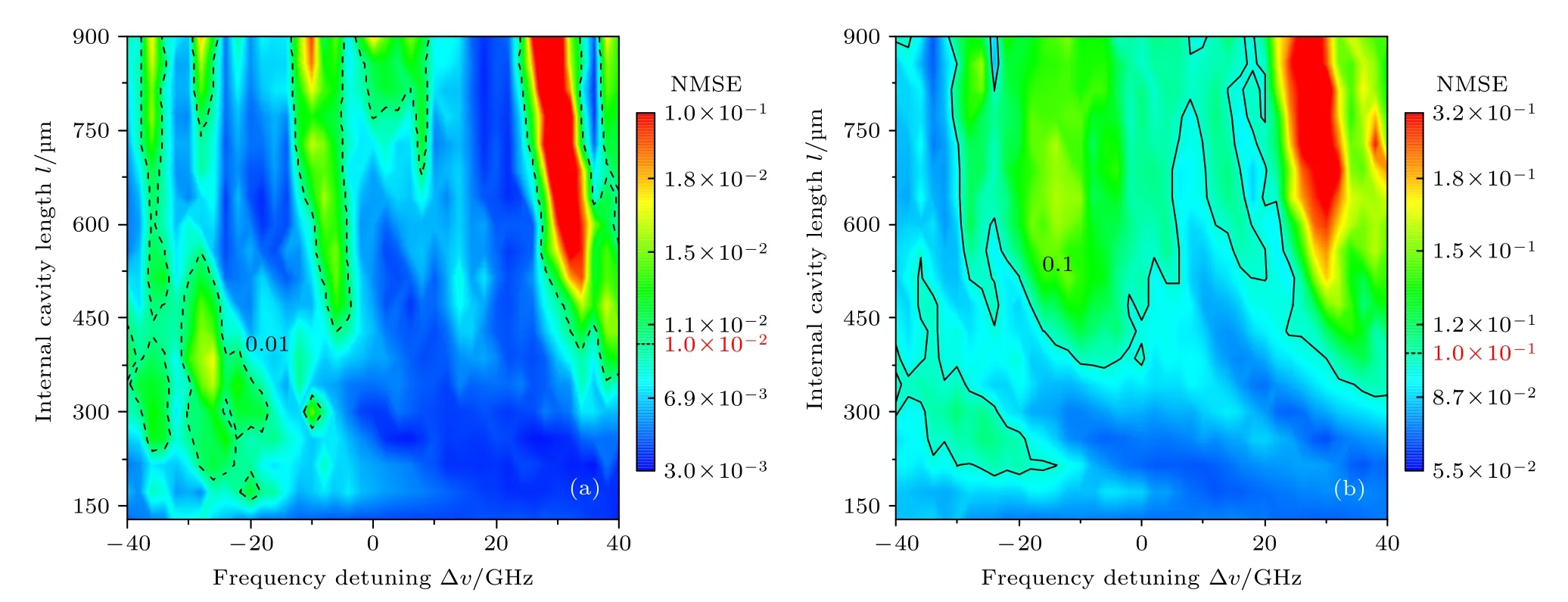
图6 在内腔长度与频率失谐参数空间中NMSEs的二维图 (a) Santa-Fe 混沌时间序列预测任务;(b) NARMA-10 任务.I=1.05 Ith,M=50,κinj=0.5,κf=0.5%Fig.6.Two dimensional maps of NMSEs in parameter space of internal cavity length and frequency detuning: (a) Santa-Fe chaotic time series prediction task;(b) NARMA-10 task. I=1.05 Ith,M=50,κinj=0.5,κf=0.5%.

3)注入强度和反馈强度范围

不同内腔长度下注入强度和反馈强度对储备池计算系统性能的影响如图7 所示,这里通过NMSE 来表征.图7 中三列图分别代表内腔长度为128,300,600 µm 时RC的处理效果,两行分别代表执行两种任务的处理效果.

Santa-Fe 混沌时间序列预测任务的处理效果如图7(a),图7(c)和图7(e)所示,其中虚线表示NMSE=0.01.从图7(a)可得,在内腔长度l=128 µm 时,NMSE 小于0.01的区域非常大,约占整个参数区域的92%,即在较大的反馈强度和注入强度范围内均可实现好的处理效果.内腔长度增大到300 µm 时相应的处理结果如图7(c)所示,可以看出虚线向右发生了偏移,此时虚线右侧区域约占整体的85%.内腔长度进一步增大到600 µm 时(如图7(e)所示),虚线继续右移.此时NMSE ≤0.01的面积已降低至参数空间的70%左右.相比于图7(a),NMSE ≤ 0.01的区域缩小了22%,且虚线右侧区域蓝色变浅,意味着系统性能有所下降.

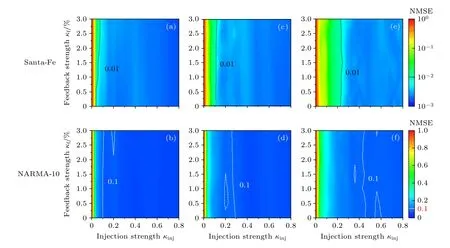
图7 不同内腔长度下注入强度和反馈强度对NMSE的影响 (a),(b) l=128 µm;(c),(d) l=300 µm;(e),(f) l=600 µm.从上到下: Santa-Fe 混沌时间序列预测任务、NARMA-10 任务.I=1.05 Ith,M=50,Δv=20 GHzFig.7.The influence of injection strength and feedback strength on NMSE under different internal cavity length: (a),(b) l=128 µm;(c),(d) l=300 µm;(e),(f) l=600 µm.From top to bottom: Santa-Fe chaotic time series prediction task,NARMA-10 task.I=1.05 Ith,M=50,Δv=20 GHz.

图7(b),图7(d)和图7(f)是系统执行NARMA-10 任务的效果,表现出与处理Santa-Fe 混沌时间序列任务相似的趋势,其中虚线代表NMSE=0.1的情况.在图7(b)中,内腔长度为128 µm 下的NMSE 低于0.1的区域占所考虑参数空间的85%左右.随着内腔长度增大到300 µm,虚线向右偏移,预测性能较好的区域减小为参数空间的65%.进一步增大内腔长度到600 µm,如图7(f)所示,虚线向注入强度增大的方向移动,相比于图7(b)NMSE ≤ 0.1的区域缩小了近40%.

总体上来看,当注入强度在0 附近时,NMSE接近于1,这意味着系统几乎没有预测性能.随着注入强度的增加,预测性能显著提升.同时,从图7中颜色深浅分布可得,随着反馈强度的增加,预测性能稍有下降.但由于色阶范围较大,NMSE 小于0.01的蓝色变化不明显.从虚线右侧所占区域面积来看,降低内腔长度,使系统预测性能良好的注入强度参数空间范围明显增大.需要说明的是,我们还分析了内腔长度更小的情况,得到了与内腔长度128 µm 相似的结果,参数空间未随着内腔长度的持续减小而扩大.

5 结论

储备池计算系统中,响应激光器短光子寿命对实现高信息处理速率有积极作用,且内腔长度与光子寿命息息相关.本文先分析了内腔长度对激光器输出的影响,其与光子寿命成线性关系.同时发现在内腔长度的改变下,激光器输出处于不同动力学状态对参数范围的要求也有明显差异.因此本文进行了内腔长度对RC 性能及参数空间影响的研究.结果表明,短内腔长度有助于获得更高的信息处理速率,在内腔长度低于171 µm 时,该系统具有实现20 Gbps 信息处理速率的潜能;内腔长度不超过514 µm 时,虚拟节点数相对较低(50)时,系统依然拥有良好的预测性能;短内腔长度下,使得系统运行良好的频率失谐范围也有相对的提升;此外,相比于600 µm的内腔长度,128 µm 内腔长度下系统执行Santa-Fe 混沌时间序列预测任务时,使系统表现出高精度预测性能的注入强度参数空间范围增大22%,且NARMA-10 任务提高约40%.这极大提高了系统的实用化,为光子集成RC 系统的实施提供了优化方案.