基于三个耦合量子点的四端混合驱动制冷机*

刘行 徐帅 高金柱 何济洲

(南昌大学物理系,南昌 330031)

本文提出了一种具有三个电容耦合量子点的四端混合驱动制冷机模型,该模型可以通过最高温的热库注入的热能和偏置电压输入的功率共同驱动来实现对低温库的制冷.基于主方程理论,分别导出了弱电容耦合和强电容耦合情况下三个量子点与四个库之间的电荷流和热流的表达式.数值模拟了制冷率与制冷系数之间的热力学性能特征曲线,在最大制冷率条件下对制冷机的主要性能参数进行了优化.最后,比较了该制冷机在强电容耦合和弱电容耦合情况下的性能.

1 引言

热电装置是运用Seebeck 效应或者Peltier 效应将环境中的热量收集起来转化为电能的发电机或者在外加偏压的条件下对某一局部区域进行制冷的冷机.然而,目前热电装置的热电转换效率仍然很低.近来,人们对开发多端热电器件越来越感兴趣,因为与传统的两端热电器件相比,多端热电器件可以通过分开电流和热流来显著提高热力学性能[1].

2011 年,Sánchez 等[2]首次提出了一种基于库仑阻塞区中两个电容耦合量子点的三端能量转换器.它可以通过从热库中吸收热能来发电,这种转换器可以在最佳配置下实现卡诺效率.后来,Thierschman 等[3]通过实验证明了这种能量转换器的工作原理.作为热机的反向操作,Zhang 等[4-6]提出了一种基于两个耦合量子点的三端量子点制冷机,详细分析了在考虑一些不可逆因素后这种制冷机的热力学性能.对于基于更多耦合量子点的三端器件,Aniket 等[7,8]提出了基于三量子点系统的实际非局部热机和制冷机,基于主方程,分析了它们的热力学性能.一些学者理论上[9-14]和实验上[15-18]研究了基于共振隧穿量子点和电容耦合量子点的许多其他三端热电装置的性能,取得长足的进展.除了共振隧穿和耦合量子点之外,其他纳米结构,包括量子阱(或半导体超晶格[19-22]、量子霍尔棒[23,24]、纳米线[25,26]、热离子[27]和能量选择性隧道结[28]也被提出用于多端热电器件.由磁振子、声子和光子等驱动源驱动的三端热电装置也得到了广泛的研究[29-37].

在三端结构热电装置的基础上,Whitney 等[38]提出了一种基于三个电容耦合量子点的四端结构热电热机,该热机即使在两个热库输入的总热功率为零的情况下,通过热曳拉效应能达到对外输出功率的效果.Su 等[39]提出了一种基于麦克斯韦妖驱动的三量子点系统的热力学泵,他们利用马尔可夫随机热力学分析了驱动泵内热力学过程.Jiang 等[40]分析了一种四端介观热电系统中库仑拖曳驱动的热电效应装置.Chen 等[41]总结了量子热力学循环,电子能量选择量子器件,量子点热管理器件等在理论和实验方面研究的代表性成果和研究进展.在前人工作的基础上,本文提出了一种具有三个电容耦合量子点的四端混合驱动制冷机模型.该模型可以通过高温的热库注入的热能和偏置电压输入的功率共同驱动来实现对低温库的制冷.相对于三端制冷机,它可以利用环境中多余的废热来驱动制冷机工作,提高能源利用.本文的重点是分析制冷率与制冷系数之间的热力学性能特征,并对制冷机在最大制冷率条件下的主要性能参数进行了优化,我们还比较了该制冷机在强电容耦合和弱电容耦合情况下的性能.

2 模型及理论

本文提出的四端热电制冷机的模型如图1(a)所示,该装置是由三个耦合量子点、两个热库和左右两个电子库组成.量子点 QDM通过两个隧道结嵌入到左右两个电子库之间,且相互之间可以进行粒子和能量的交换,其中左侧电子库L的温度为TL以及化学势为µL,右侧电子库R的温度为TR以及化学势为µR.量子点 QDH与温度为TH,化学势为µH的热库H 耦合,而量子点 QDC与温度为TC,化学势为µC的中间温度的热库耦合.三个量子点QDM,QDH和 QDC相互耦合并且通过长程库仑作用相互影响.采用UMH,UMC和UHC来表示充电能.如果量子点彼此距离较远,它们可以桥接,以获得强/弱耦合,同时又能确保电子库和热库之间形成良好的热隔离.四端结构热电热机的等效电路图如图1(b)所示.

图1 (a) 基于三量子点耦合的四端制冷机的示意图;(b) (a)中装置的等效电路图Fig.1.(a) Schematic diagram of a four terminal refrigerator based on three coupled quantum dots,and (b) is the equivalent circuit diagram of the device in (a).

三个耦合的量子点QDM,QDH和QDC,都有各自的单能级εM,εH和εC.中心系统的量子态可以表示为(m,h,c),其中m,h和c分别表示各个量子点能级上的电子占据数.因为库仑相互作用阻止两个电子同时出现在同一个能级上,所以三个量子点的单能级εM,εH和εC上各自只能有一个电子或者没有电子.该系统存在8 种量子态,它们分别为(0,0,0),(1,0,0),(0,1,0),(0,0,1),(1,1,0),(1,0,1),(0,1,1),(1,1,1),8 种量子态相互转换的动力学过程如图2 所示,其中表示由于电子隧穿进入库α或者隧穿流出库α(α=S,H,C 和S=L,R)而使得该三量子点中心系统从量子态(m′,h′,c′)跃迁到量子态(m,h,c)的速率.

图2 图1 描述的八种量子态的跃迁过程Fig.2.The transition processes of eight quantum states described in Fig.1.

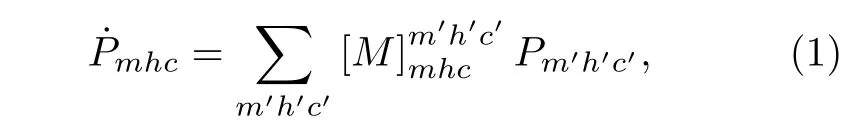
当TH＞TL(R)＞TC时,该装置可作为一种利用从高温热库H 流出的热流JH和外加电压输入的功率共同驱动来实现对低温热库C 制冷的混合驱动制冷机,称之为装置A.此时的JH,JC,JLR,P四个参数应该满足:

此时,JC可被视为制冷机的制冷率,此时的制冷系数定义为

当输入功率P=0 时,该装置可作为一个纯热驱动制冷机,制冷系数ηCOP=JC/JH.当高温热库输入的热流JH=0 时,该装置可作为一个纯电驱动制冷机,制冷系数ηCOP=JC/P.

当TH＞TC＞TL(R)时,该装置可作为一种利用高温热库H 释放的热流JH和外加电压输入的功率共同驱动来实现对低温系统LR 制冷的混合驱动制冷机,称之为装置B.此时的JH,JC,JLR,P四个参数应该满足:

其中JLR为制冷率,制冷系数定义为

可以绘制出当耗散系数为λ=0 时,输入功率P以及各量子点与对应库之间的热流JH,JC,JLR随温差 ΔT和偏置电压eΔV变化的三维投影图.如图3 所示,图中的黑线对应P=0,红线代表JH=0,蓝线表示JC=0,黄线表示JLR=0 .

图3 当耗散系数为λ=0 时,(a) 输入功率 P 以及(b)—(d)各量子点与对应库之间的热流JH,JC,JLR 随温差 ΔT 和偏置电压eΔV 变化的三维投影图Fig.3.The three-dimensional projection graphs for (a) input power P and (b)—(d) the heat flow JH,JC,JLR varying with the temperature difference ΔT and the bias voltage eΔV under the dissipation factor λ=0 .

当耗散系数为λ=0 和λ=0.26 时,装置A 和装置B 各自对应的工作区域,如图4 所示.通过数值计算,发现装置A 和装置B 对应的工作区域都随着耗散系数的增大而减小.且当λ≥0.015 时,装置B 会消失.当λ≤0.26 时,装置A 只有一种工作模式,即混合驱动制冷机,当λ≥0.26,装置A 有两种不同的工作模式,即混合驱动制冷机和纯电驱动制冷机.与装置A 相比,装置B 更为复杂,因为子系统LR 既是电力的驱动端,又是制冷的目标.虽然装置B的制冷率明显小于装置A,但可以在装置A 不能工作的区域工作,进而实现不同的制冷效果.

图4 当耗散系数为λ=0 和 λ=0.26 时,装置A 和装置B 各自对应的工作区域Fig.4.The corresponding working areas of device A and device B when the dissipation factor is (a) λ=0 and (b) λ=0.26,respectively.

本文仅分析装置A 即混合驱动制冷机的性能特征.可以画出在不同耗散系数下,装置作为混合驱动制冷机时的总熵产率随温差 ΔT和偏置电压eΔV变化的三维曲线,如图5 所示.其中绿色面对应λ=0,红色面对应λ=0.1,蓝色面对应λ=0.2 .发现总熵产率满足的S˙＞0,并且S˙ 随着耗散系数的增加而增加.

图5 在不同耗散系数下,装置作为混合驱动制冷机时的总熵产率随温差 ΔT 和偏置电压 eΔV 变化的三维曲线Fig.5.The three-dimensional curves of total entropy production rate varying with temperature difference ΔT and bias voltage eΔV when the device is used as a hybrid-driven refrigerator under different dissipation factor.

为了简化制冷率和制冷系数并明确各种参数之间的关系,制冷率和制冷系数可以重新写成

根据以上各公式,对于给定的ΔT=2γ/kB和eΔV=50,绘制出在不同的耗散系数下制冷率和制冷系数随充电能UMH和UMC变化的三维图,如图6 所示.可以看出对于耗散系数为λ=0,当满足UMH/γ=50和UMC/γ ≃19.5 时,可以得到最大制冷率,当满足UMH/γ=50和UMC/γ ≃23 时,可以得到最大制冷系数.且最大制冷率和最大制冷系数均随耗散系数的增大而减小.

图6 在不同耗散系数下,制冷率和制冷系数随充电能 UMH 和 UMC 变化的三维图Fig.6.The three-dimensional diagrams of the cooling rate and the COP varying with charging energy UMH and UMC under different dissipation factor.

在不同的耗散系数下制冷率和制冷系数随充电能UMH和偏置电压eV变化的三维图,如图7 所示.可以看出,制冷率随着偏置电压的增大而增大.

图7 在不同的耗散系数下,制冷率和制冷系数随充电能 UMH 和偏置电压 eV 变化的三维图Fig.7.The three-dimensional diagrams of the cooling rate and the COP varying with charging energy UMH and bias voltageeΔV under different dissipation factor.

3 优化性能分析

根据 (1)—(5) 式,(10)和(11)式以及极值条件:

在给定条件 ΔT=2γ/kB下,优化的制冷率JCopt和优化制冷率对应的制冷系数随耗散系数λ的变化曲线,如图8 所示.优化的制冷率和对应的制冷系数随耗散系数λ的增大而单调递减,只有当λ=0时,才能得到优化的制冷率最大值和对应的制冷系数的最大值.为了获得最大的制冷率和相应的制冷系数,应该选择尽可能小的耗散系数.本文采用了UMH/γ=50,eΔV=50 进行数值计算.

图8 在给定条件 ΔT=2γ/kB 下,(a) 优化的制冷率 JCopt 和(b)优化制冷率对应的制冷系数以及(c)对应的充电能 UMC 随耗散系数 λ的变化曲线Fig.8.The curves of (a) the optimized cooling rate JCopt and (b) the COP corresponding to optimized cooling rate and (c) the corresponding charging energy UMC as a function of dissipation factor λ under the given condition ΔT=2γ/kB .

分析温差 ΔT对混合驱动制冷机最优性能的影响.利用(16)和(17)式,只对最大制冷率对应的充电能UMC进行优化,而直接取充电能、优化偏压和优化耗散系数为UMH/γ=50,eΔV=50 和λ=0.可以绘制出最大制冷率JCmax、最大制冷率对应的COPηJ、最佳充电能量UMC随温差 ΔT的变化曲线,如图9 所示.从图9(a)可以看出,最大制冷率JCmax、最大制冷率对应的COPηJ会随着温差 ΔT的增大而逐渐减小.由图9(b)可知,最佳充电能量UMC随温差 ΔT的增大而单调减小.

图9 (a) 最大制冷率 JCmax 和最大制冷率对应的COP ηJ ;(b) 最佳充电能量 UMC 随温差 ΔT的变化曲线Fig.9.The curves of (a) the maximum cooling rate JCmax and the COP corresponding to maximum cooling rate ηJ and (b) the optimal charging energy UMC as a function of temperature difference ΔT .

4 强耦合UHC

当量子点 QDH和 QDC之间是强耦合UHC时,则量子点 QDH和 QDC同时被占据的可能性就变得很小,所以就不存在量子态(0,1,1)和(1,1,1),此时中心系统仅存在6 个量子态.电荷涨落可分为两个循环,第一个循环是:

涉及到系统和高温热库之间的交换能量UMH.第二个循环是:

涉及到系统和次高温热库之间的交换能量UMC.从左侧电子库L 到量子点 QDM的电子流表达式为

从右侧电子库R 到量子点 QDM的电子流表达式为

从左侧电子库L 到量子点 QDM的热流表达式为

从右侧电子库R 到量子点 QDM的热流表达式为

从高温热库H 到量子点 QDH的热流表达式为

从次高温热库C 到量子点 QDC的热流表达式为

通过数值计算,绘制出该混合驱动制冷机在强耦合UHC的情况下,当λ=0 时制冷率JC和制冷系数ηCOP随UMH和UMC变化的三维图,如图10 所示.与弱耦合的情况相比,强耦合作用下最大制冷率和制冷系数要大得多.

图10 在强耦合 UHC的情况下,当 λ=0 时,(a) 制冷率 JC 和(b)制冷系数 ηCOP 随着 UMH 和 UMC 变化的三维图Fig.10.In the case of strong coupling UHC,when λ=0,the three-dimensional diagrams for (a) cooling rate JC and (b) the COP varying with UMH and UMC .

5 结论

本文研究了利用高温热源释放的热能和外加电压输入电能共同驱动来实现对低温库制冷的四端三量子点制冷机的性能.主要研究结论: 1)混合驱动制冷机的工作区域、制冷率和制冷系数均随耗散系数的增大而减小;2)最大制冷率和对应的制冷系数COP 随着温差 ΔT的增大而减小;3)通过合理选择充电能UMC,使λ=0,并使充电能UMH和eΔV尽可能大,可以使混合驱动制冷机在最大制冷率的最佳状态下运行;4)与弱耦合的情况相比,强耦合作用下最大制冷率和制冷系数要大得多.