基于专家PID算法的转差频率控制策略研究
2022-10-15刘万兵鲁西坤雷慧杰
刘万兵,鲁西坤,雷慧杰
(1.河南安彩高科股份有限公司,安阳 455000;2.安阳工学院,安阳 455000)
0 引 言
恒压频比控制和转差频率控制是交-交变频调速系统中应用广泛的标量控制方法[1-2]。恒压频比控制方式是保证运行过程中的磁通量恒定,它主要根据电机的额定电压与频率的比值,来调整变频器输出的电压和频率,从而实现对电机的调速。这种控制方式尤其适用于恒转矩负载的控制,是简单、实用的开环调速方法[3-5]。转差频率控制则是闭环控制,是在恒压频比的基础上进行的改进。在电机稳态运行时,转差率近似与输出转矩成正比。根据这一特性,可以通过调整转差率来控制系统的输出转矩,从而控制系统的转速[6-8]。在调速过程中,系统的稳态精度、动静态性能和抗干扰能力均优于恒压频比控制。转差频率控制是目前公认的一种性能良好的变频调速控制方式,同时也是高校电气传动、电机拖动等课程的重要知识点[9-10]。然而,其模型的推导是基于稳态条件,严格地说,系统的转矩和磁通量并没有得到理想的控制。
为了实现转差频率控制系统更好的调速效果,提高系统的控制精度,本文引入了专家PID控制算法,针对转差频率控制做了大量的实验和仿真,从中总结出规律,建立起专家知识库,并验证了所设计的系统具有较好的动态和静态性能,反应时间短,控制精度高。
1 转差频率控制策略
按照转差频率控制的原理,根据交-交变频器的结构特点,绘制出转差频率控制系统的原理图,如图1所示。速度闭环是根据给定速度与速度反馈之间的差异,通过速度调节器(ASR)的调节作用来计算系统的转差频率。电流闭环的采样点位于变频器的输入端,能准确检测系统的电流值,然后经过主控芯片的AD转换功能,将转换过来的电流值同函数发生器产生的定子电流值I1相比较,经过电流调节器(ACR)调整后,同脉冲触发序列一起,确定下一时刻系统的输出电流值,最后根据电机的电压平衡方程确定系统的输出电压值。

图1 转差频率控制框图
2 专家PID原理及实现
专家控制系统是根据基于知识或经验专家知识库和逻辑推理,实现对系统的控制[12]。专家PID结构如图2所示。该结构主要分为专家知识库和逻辑推理两个功能模块,图2中的各项功能主要在控制芯片编程实现,主控芯片根据监测到的当前系统转差频率、电流、电压等参数,对PID控制器的参数进行调整,同时计算下一时刻系统的电压、电流和输出频率,以实现对转差频率的控制,实现过程如图3所示。

图2 专家PID控制原理框图
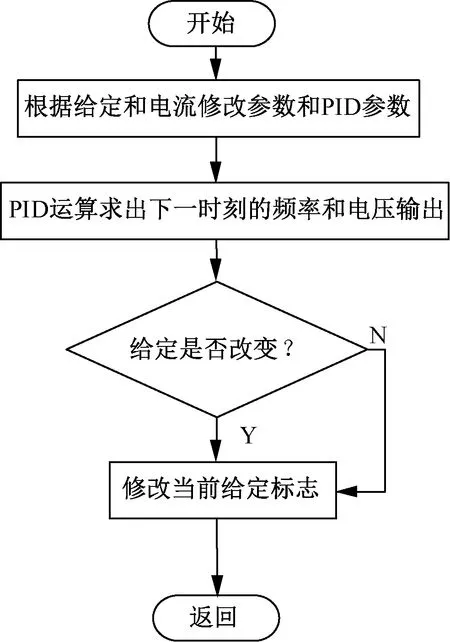
图3 专家PID程序流程
专家PID控制算法最主要的一点是,系统能够根据系统运行的状态,自动搜索已建立的专家知识库,从而选择合适的PID参数,达到调速的目的。通过调整PID各项参数,实现改变转差频率系统调速性能的目的。PID各参数调整趋势如下:增大积分系数D可以加快响应速度和减小超调量;增加比例系数能够达到减少稳态误差和缩减响应时间的效果;减小微分系数同样能够减小超调量。因此,PID控制具体规则分以下几种情况。
1)|e(k)|>Ml,系统的偏差很大,此时应考虑加强控制器积分环节的作用,达到快速响应,减小超调的效果。表达式:
u(k)=u(k-1)+k1K1e(k)
(1)
2)Mm<|e(k)|
u(k)=u(k-1)+k1{KP[e(k)-e(k-1)]+
KIe(k)+KD[e(k)-2e(k-1)+e(k-2)]}
(2)
如果e(k)Δe(k)<0,即偏差在减小,应该采用加强的比例作用,算式如下:
u(k)=u(k-1)+k1KPe(k)
(3)
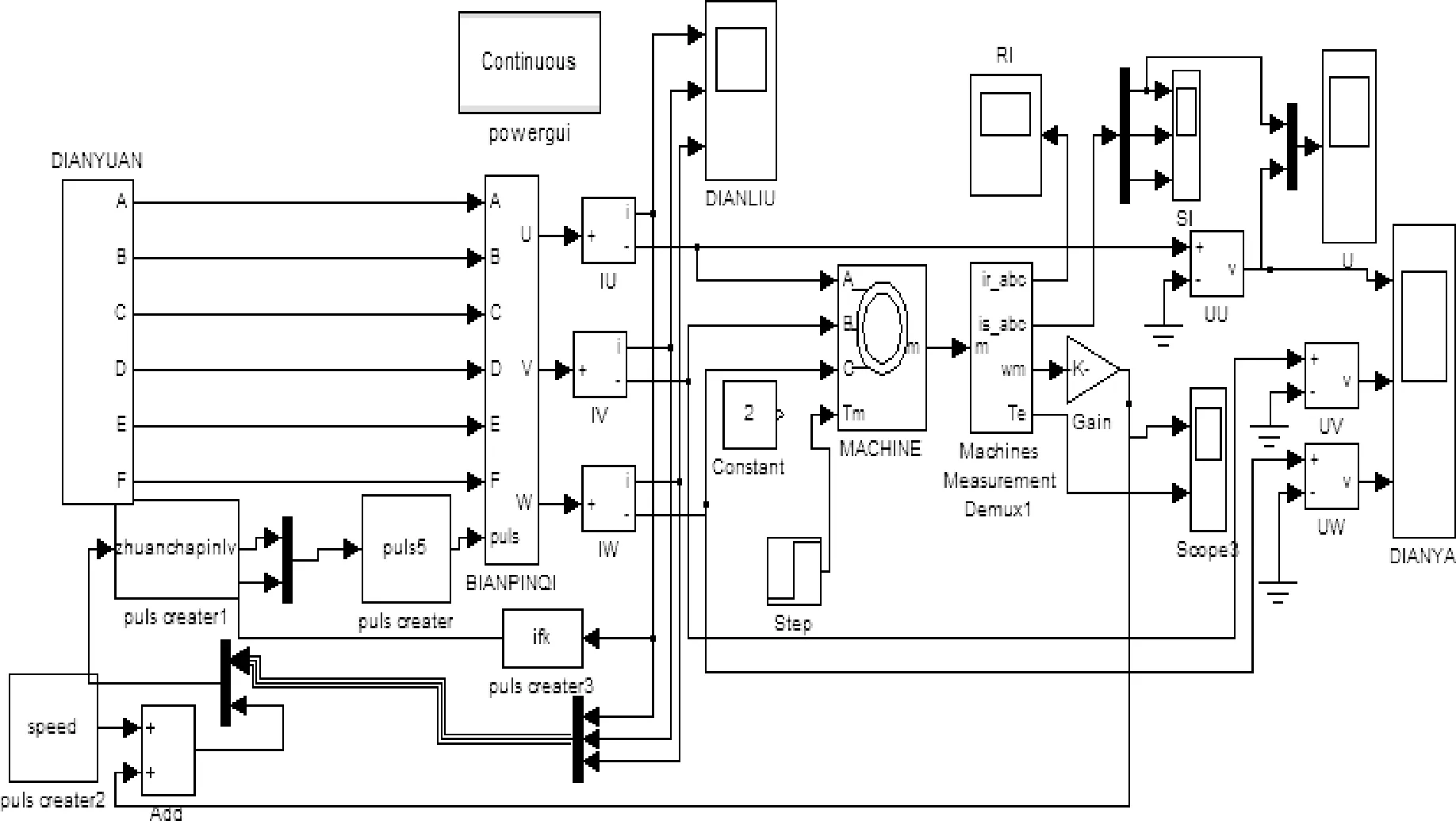
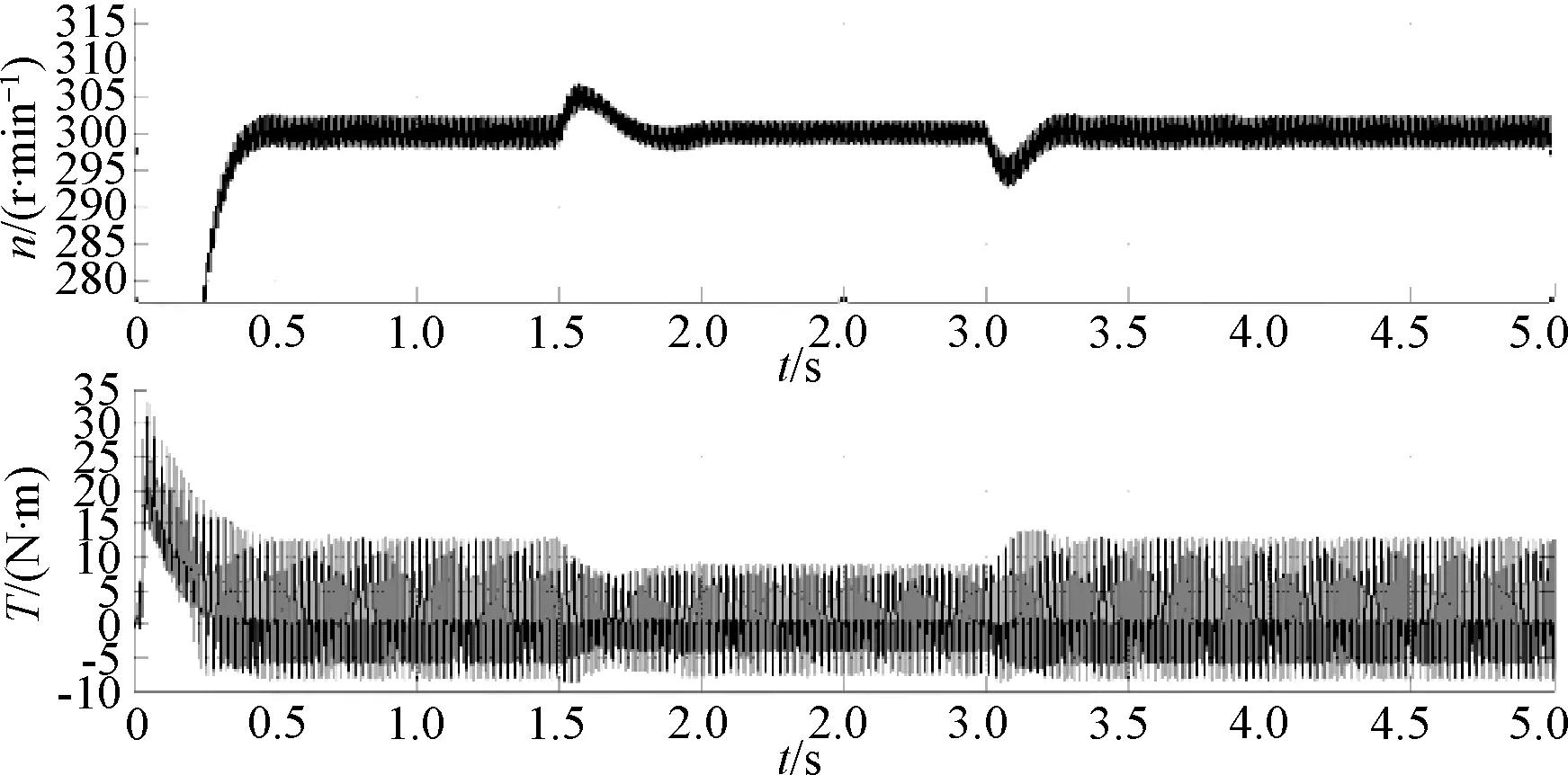
3)Ms<|e(k)| u(k)=u(k-1)+KP[e(k)-e(k-1)]+ KIe(k)+KD[e(k)-2e(k-1)+e(k-2)] (4) 4)ε<|e(k)| u(k)=u(k-1) (5) 如果e(k)Δe(k)<0且Δe(k)Δe(k-1)<0,此时系统出现了平衡状态附近的振荡。为了消除系统振荡,应调整控制器表达式: u(k)=u(k-1)+k2KP[e(k)-e(k-1)] (6) 5)|e(k)|<ε时,系统偏差很小,为消除系统静差,调整PID控制器为PI环节,即: u(k)=u(k-1)+KIe(k)+KP[e(k)-e(k-1)] (7) 式(1)~式(7)中:e(k)为当前转速给定与实际值之差;e(k-1)为上一采样时刻转速给定与实际值之差;u(k)为当前系统输出;u(k-1)为上一采样时刻系统输出;KP为系统比例系数;KI为系统积分系数;KD为系统微分系数;k1是PID控制器放大系数;k2是PID控制器抑制系数。 多次实验得到系统偏差很小(ε)、较小(Ms)、较大(Mm)、很大(Ml)等参数,如表1所示。 表1 PID结构调整参考值 在MATLAB/Simulink环境下,按照转差频率和专家PID算法原理,搭建转差频率控制系统的仿真模型,编写S函数来实现PID算法,仿真模型如图4所示。该仿真模型中的主电路是六相电源模块、脉冲触发及晶闸管模块和电机模块,其中六相电源模块主要是给系统提供电源,是相邻两相互错60°的工频交流电源。脉冲触发模块主要功能就是将S函数模块的36路输出信号转化为对应于晶闸管模块中的36只晶闸管的触发信号,从而来触发相对应的晶闸管。晶闸管电路模块采用零式接法,每一相输入电源上都接一对反并联晶闸管,这样就可以保证电流能够正、反向流过。具体的晶闸管的触发时刻则由触发S函数模块的输出决定。电机模块是整个系统的被控器件,并且可以根据实际电机的规格参数来调整其各项参数。仿真模型中的控制部分包括系统的速度和电流反馈、速度给定模块、触发S函数模块以及实现转差频率控制的S函数模块。 图4 转差频率控制系统仿真模型 给定转速为300 r/min,初始负载转矩为3 N·m的情况下,转差频率控制调速效果如图5所示。从图5中可以看出:开始仿真后,电机能够快速起动,并达到给定转速,整个过程中无超调出现;负载发生突变后,转速迅速变化,并在转差频率控制下,迅速恢复并稳定在给定值,从而证明了专家PID算法下的转差频率控制系统能够较好地满足系统的动静态性能要求。 图5 负载突变时仿真结果 交-交变频转差频率系统的控制回路可以分为转速反馈、电流反馈、控制电源、同步信号检测、脉冲触发模块和信号检测模块等部分,其结构框图如图6所示。 图6 系统控制电路框图 本系统的信号检测环节分为电流(包括小电流检测)、电压以及速度检测等模块。电压和电流检测模块分别采用霍尔电压、电流传感器,其型号为KV50A/P和KA50A/P。信号经过处理之后,可通过示波器观察其波形。小电流检测部分是为了实现系统的电流无死区换相控制策略而设计的检测电路。速度检测模块采用光电编码器,其每转发出200个计数脉冲,选用型号为OVW2-1024-2MHT,该脉冲序列需经过整形和隔离后,方能传入到控制器中,通过一定的采样频率和系统定时器来计算转速。 专家PID算法下转差频率控制系统的主程序如图7所示。该系统的主程序同其他系统的主程序相似,需要先对系统时钟的设定、中断、定时器、GPIO口和串口等系统用到的各个模块进行初始化操作。 图7 系统主程序流程图 在建立专家库和加入专家PID算法后,可以优化转差频率控制策略,其程序流程图如图8所示。根据检测到的系统转速和电流,计算得到系统当前转差频率,同时验证电流和转差频率是否满足I1=f(ωs)关系,进而根据专家PID算法,调节系统的PID参数,得到下一时刻系统的输出频率和电压值。 图8 转差频率控制子程序框图 图9和图10分别为普通闭环控制情况下的电机空载起动效果和专家PID算法下转差频率控制的电机空载起动效果。设定电机的给定转速为300 r/min,由图9可以看出,系统能够按照给定的转速起动,起动过程比较慢,用时4.5 s才到达给定转速300 r/min,且出现了超调现象,从起动到稳定,系统共用时11 s,用时较长。从图10可看出,在加入了转差频率控制和专家PID算法后,系统能够快速地起动,1.5 s到达给定转速,且起动过程中转速波动较小(约为2.5%),无超调现象出现。 图9 普通闭环控制起动效果 图10 转差频率控制起动效果 图11是系统初始转速给定为520 r/min,初始负载转矩为2.4 N·m情况下的调速效果。图11中,系统可以快速地起动,起动过程稳定,无振荡现象,但是起动过程出现了微小的超调,其超调量为0.8%;进入稳定状态后,系统能够稳定在给定转速下运行,且波动不大;当系统转矩突然增加到3.2 N·m,系统的输出转矩没有发生突变,导致当前的输出转矩不能使电机维持在给定转速下,转速立即下降到485 r/min左右,然后又迅速恢复到520 r/min,重新回到稳定状态。整个过渡过程共约2 s,速度降幅为6.7%,在回复到给定转速的过程中,系统没有出现振荡,也没有超调现象。这是因为在系统调速过程中,根据专家PID控制算法,改变了系统的参数,提高了系统的响应速度和控制精度。 图11 突加负载时调速效果 本文在对转差频率控制分析的基础上,提出了运用专家PID算法去实现转差频率控制,并根据交-交变频器的特点,搭建了仿真模型和实验电路,对转差频率控制的仿真和实验结果进行了对比分析,得到了在转差频率控制策略中加入了专家PID算法,使系统的适应性和动态性能得到改善,同时降低了系统的稳态误差,有利于实现工业控制中对各种工况的需求。
3 转差频率控制系统仿真
4 交-交变频转差频率调速系统实现
4.1 转差频率控制硬件电路

4.2 系统主程序设计

4.3 转差频率控制算法子程序设计

4.4 实验结果分析



5 结 语
