线性压缩机直线电机超低振动输出特性研究

蒋珍华，项汉桢，丁 磊，黄 政，陆 志，刘少帅，吴亦农，曲晓萍

(1.中国科学院上海技术物理研究所，上海 200083；2.中国科学院大学，北京 100086)

0 引 言

近年来低温制冷技术飞速发展，在航天红外探测领域的应用越来越广泛。一方面，制冷型红外探测器必须在低于某一温度下才能正常工作，获得较高的灵敏度、分辨率和信噪比[1-2]；另一方面，低温环境可以减轻探测视场内零部件的热辐射背景干扰，提高探测灵敏度[3]。因此，对长寿命、高效率、低振动、轻量化的低温制冷机的研究尤为迫切。

低温制冷机由压缩机和膨胀机组成，压缩机是制冷机的心脏，为系统提供动力。压缩机中的电机带动活塞做直线往复运动为冷指提供压力波，是电功转换为机械功的重要部件，负载刚度与动子质量的匹配性决定了电机效率，进而影响制冷机效率[4-5]。文献[6]用等效磁路法分析了动磁式线性压缩机的电机结构，得出电磁推力与励磁电流和电动机几何尺寸等参数的相关数学关系式，为动磁式压缩机的设计奠定了基础。但动磁式压缩机的径向颤振较大，应用较为局限。本文以低颤振的动圈式压缩机为例，进行等效磁路分析，得到了电机效率与各参数之间的关系式，并与有限元仿真相结合，获得了电机各参数对电机效率影响的数值规律。

压缩机设计时通常采用对置式活塞设计方式以抵消轴向颤振力，由于两侧电机的磁性能、活塞的尺寸、动子的质量等无法保证完全一致，实验测试中仍会发现压缩机有比较明显的轴向颤振，这种颤振将影响红外载荷的探测精度[7]。文献[8]设计了一种被动减振器来抑制斯特林制冷机的轴向颤振，发现只有当减振器与制冷机的固有频率与驱动频率均相等时，才能消除斯特林制冷机的颤振。此种方法需要额外增加体积和质量，且对被动减振器的固有频率精度要求高，若存在谐振偏差，减振效果将受到影响。制冷机安装至整机后，会影响减振器安装路径上的阻尼，使其固有频率发生偏移，导致减振效果变差。本文依据理论分析，从根源入手，分析压缩机产生颤振的具体原因，模拟分析了电机运行状态参数对颤振力的量化影响，给出了抑制颤振力的调整方法并进行了实验验证，从压缩机本体出发将颤振降至较低水平。

1 双动圈直线电机设计

1.1 双动圈式直线电机结构

本文设计的双动圈式直线电机结构如图1所示。电机的静子部分由上下主磁钢、上下端部磁环、中间磁环、内外磁极组成，其中上下主磁钢径向充磁，中间磁环和上下端部磁环轴向充磁，内外磁极采用高磁导率的软铁材料。电机的动子部分由活塞、活塞轴、双段线圈、柔性板簧组成，其中活塞轴与双段线圈通过线圈骨架螺接在一起，套在活塞轴上的柔性板簧通过轴端螺母固定，整体构成弹簧振子系统[9]。线圈通入正弦交流电时，受安培力作用，带动压缩活塞进行往复直线运动，在压缩腔内形成压力波。

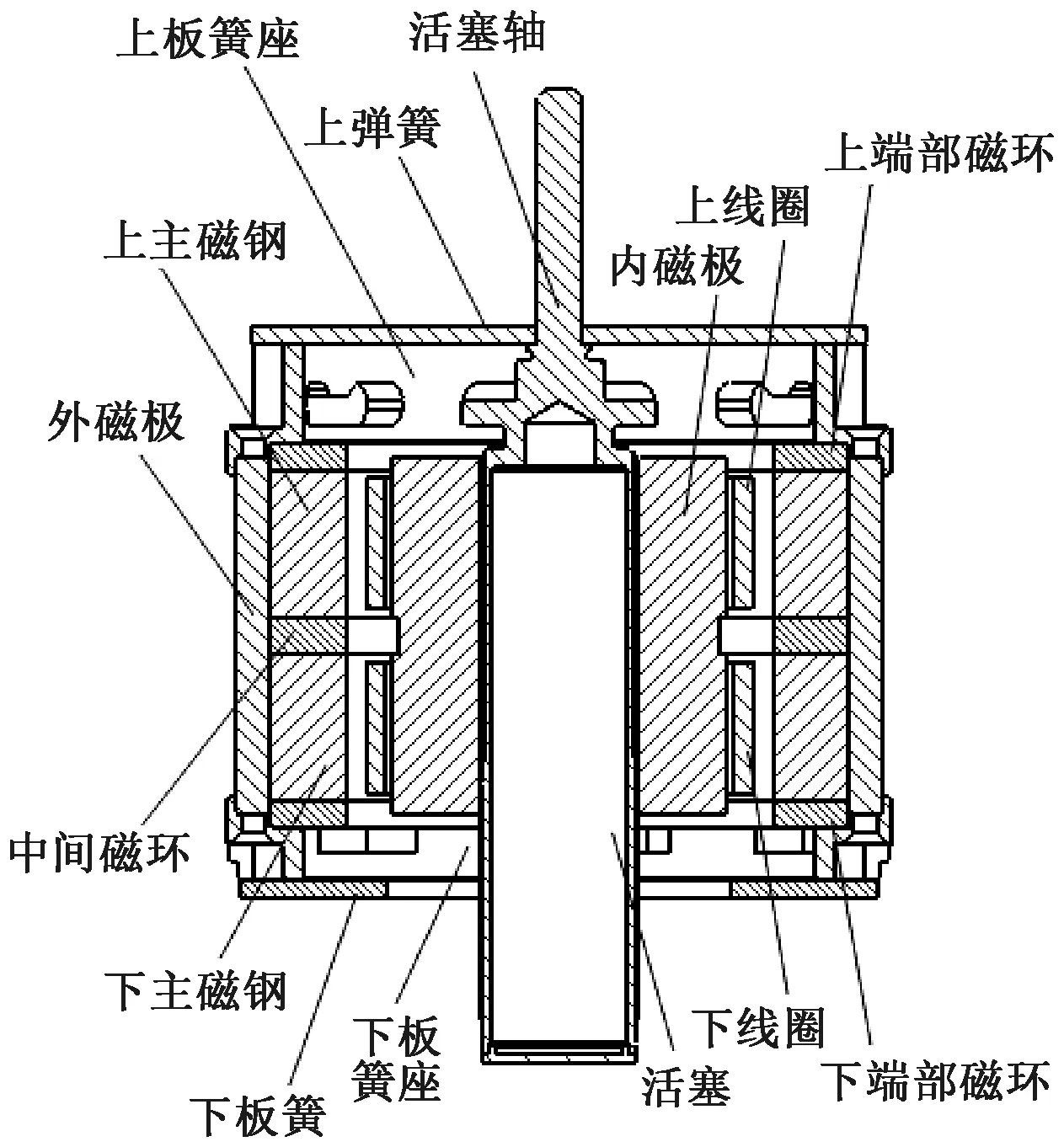
图1 双动圈式直线压缩机结构示意图

磁钢的这种排列组合为Halbach阵列[10-11]，可以在有限的体积内较大地增加单侧磁场强度。对比相同磁路尺寸的Halbach阵列磁路和非Halbach阵列磁路，当所有永磁体牌号均为N50H时，如图2所示，非Halbach阵列气隙磁场区域内特定点处的磁感应强度为368 mT，Halbach阵列气隙磁场区域内相同点处的磁感应强度为758 mT，磁场强度增加了106%，磁场强度得到了显著的提升。同时由表1可知，非Halbach阵列电机外侧发散在空间特定点的磁感应强度为336 mT，相同点处Halbach阵列的磁感应强度为154 mT，下降了54%，说明Halbach阵列磁钢减小了电机的漏磁，可以大幅降低磁干扰对探测器重要元器件的影响。

图2 永磁体阵列磁感应线图

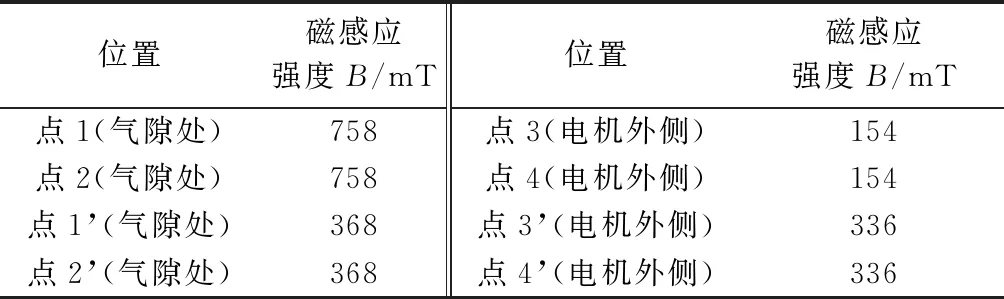
表1 不同磁钢阵列关键点处的磁感应强度

由电机组件的磁路结构及磁感应线分布可知，线圈通入交流电进行往复运动的过程中，主要受到安培力的作用，安培力推动线圈进行轴向运动。为了进一步分析安培力F=BIL与电机效率的关系，建立如图3(a)所示的电机模型。上下线圈串联，但绕向相反，当其通入正弦交流电时，两个线圈产生的磁动势NI大小相等、方向相反，互相抵消，且上下端部磁环与中间磁环辅助增加了主磁钢的磁场强度，为了简化磁路分析，仅考虑主磁钢的磁动势对整个磁路的作用。图3(b)为电机的等效磁路图[12]，Fm1、Rm1分别为上主磁钢的磁动势和磁阻，Fm2、Rm2分别为下主磁钢的磁动势和磁阻，Rδ1、Rδ2分别为上气隙磁阻和下气隙磁阻；Rτ1、Rτ2分别为上气隙边缘磁阻和下气隙边缘磁阻，R1、R2分别为内外磁极的磁阻。

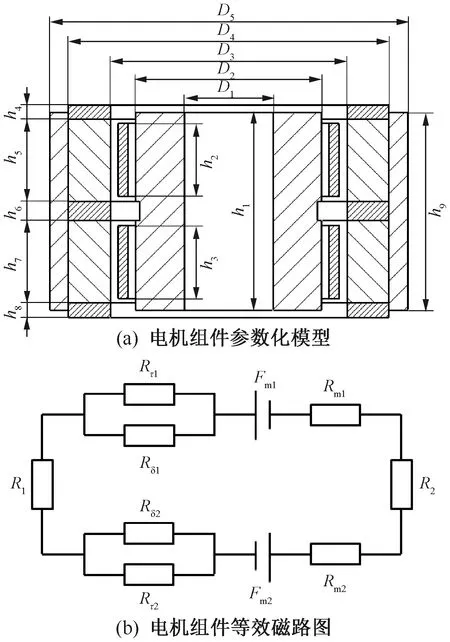
图3 电机组件图

磁路磁阻的计算公式如下：

R=h/(μA)

(1)

式中：h为磁阻单元的长度；μ为磁阻单元的绝对磁导率；A为磁阻单元的横截面积。为了简化计算，按内外磁极轴线方向计算磁阻，此时两者的磁阻：

(2)

(3)

式中：μr1为内外磁极的磁导率；D1为内磁极内径；D2为内磁极外径；D4为磁钢外径；D5为外磁极外径；h1为内磁极轴向厚度；h9为外磁极轴向厚度。当内外磁极无磁饱和现象时，其磁导率较高，磁阻较小，此时消耗的磁动势集中于气隙和永磁体上，两者的形状均为环形，扇环形磁阻单元的径向磁路磁阻按下式计算：

Rr=ln(r2/r1)/(μlπ)

(4)

式中：r1为环形磁阻单元内圆半径；r2为环形磁阻单元外圆半径；l为磁阻单元的轴向长度。由于h5=h7，根据图3(a)中的尺寸，结合式(4)可得永磁体和间隙磁阻如下：

Rm1=Rm2=ln(D4/D3)/(μ0μr2h5π)

(5)

Rδ1=Rδ2=ln(D3/D2)/(μ0h5π)

(6)

式中：D3为磁钢内径；h5为主磁钢轴向厚度；μ0为真空磁导率；μr2为永磁体的相对磁导率，通常取μr2=1.05。考虑到磁感应线通过气隙时会产生边缘磁阻，即非垂直穿过线圈的磁感应线产生的磁阻，得边缘磁阻[13]：

Rτ1=Rτ2=Rδ1/(τ-1)

(7)

根据本文的电机结构，取边缘磁阻系数τ=1.2。上下永磁体产生的磁动势:

Fm1=Fm2=HcB(D4-D3)/2

(8)

式中：HcB为磁感矫顽力。通过图3(b)可知，磁路的总磁通:

φ=(Fm1+Fm2)/(R1+R2+Rm1+

Rm2+5Rδ1/6+5Rδ2/6)

(9)

假定软磁材料的磁导率μr1不变，将与尺寸无关的正系数分别设置为K1、K2、K3，可得气隙处的平均磁感应强度:

K3ln(D3/D2)}(D2+D3)}

(10)

式中,K1、K2、K3的表达式分别如下:

K1=1/(πHcBμr1)

(11)

K2=1/(2πHcBμr2μ0)

(12)

K3=5/(12πHcBμ0)

(13)

电机线圈受到的驱动力F=BIL，此时的电机效率：

η=(Fv)/(Fv+I2R)=

1/[1+ρI/(BvS)]

(14)

式中：ρ为电阻率;v为活塞运动速度;I为电流;S为线圈的横截面积;B为气隙磁感应强度。由式(14)可知，当压缩机活塞直径、绕线和气体负载不变时，ρ、υ、S均不变，且电机效率与气隙磁感应强度成正比，气隙磁感应强度与主磁钢内外径、轴向长度、内外磁极内外径、轴向长度、气隙内外径均相关。

1.2 双动圈电机主要参数性能影响

依据上述等效磁路分析法，对有负载时压缩机电机不同结构参数对电机性能的影响进行量化分析，图4为有气体负载时的压缩活塞受力图，其中Fe为电机的驱动力。

图4 压缩机活塞受力分析图

基于Maxwell仿真平台开展在热力负载下压缩机的电机仿真分析，以式(14)为基准对影响电机质量和电机效率的内磁极内外径、外磁极内外径、磁钢内外径进行精细化仿真，得到性质比最高的电机结构。以内磁极径向厚度7.7 mm、磁钢径向厚度6.5 mm、外磁极径向厚度3.0 mm的初始电机模型进行分析。

在初始模型上仅改变内磁极径向厚度，其余部件的内外径随变，内磁极径向厚度变化引起的电机质量和效率变化曲线如图5所示。

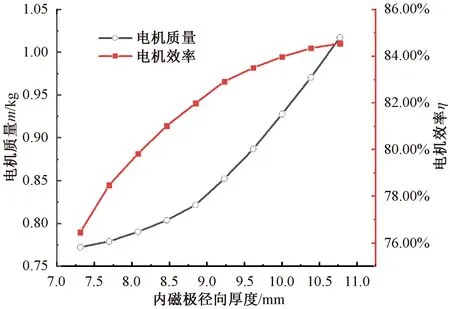
图5 内磁极径向厚度对电机效率的影响

电机效率增速随内磁极径向厚度的增加先快后慢，根据式(10)，增加内磁极径向厚度，即增加(D2-D1)/2，D4-D3不变，但分母减小，使气隙磁感应强度B持续增大，通过式(14)可知，电机效率持续增大。但两式默认软磁材料的磁导率为定值，实际情况下，软磁材料的磁导率随着磁场强度的变化先大后小，且当通过软磁材料的磁感应强度太大时会产生磁饱和现象，此时剩下的磁感应线不再进入软磁材料。在该模型中，永磁体产生的磁动势不变，限制了气隙磁感应强度B的上限，增大内磁极厚度，仅缓解了磁饱和现象，所以电机效率的增速呈现先急后缓的趋势变化，但电机质量随着内磁极的增大而呈二次方关系增加。折中质量和效率，选定图5中内磁极厚度为10 mm时对应的电机模型，此时电机效率为83.98%。

为了进一步提升效率，采用增加磁钢径向厚度,即增加(D4-D3)/2的方法增加磁路的磁动势，如图6所示。随着磁钢厚度的增加，式(10)中D4-D3的变化幅度远大于K2ln(D4/D3)的变化幅度，气隙磁感应强度B一直增大，电机效率随之增加。电机效率增加趋势先急后缓，这是因为磁钢产生的磁动势增加，通过内外磁极的磁通量变大，而内外磁极的径向厚度不变，磁场越来越趋于饱和，使电机效率增速变缓。

图6 磁钢径向厚度对电机效率的影响

选取磁钢径向厚度为8.8 mm时为最优，此时电机效率为86.72%。当内磁极与磁钢径向厚度分别为10 mm、8.8 mm时，改变外磁极径向厚度，即改变(D5-D4)/2，电机效率和质量的变化曲线如图7所示。

图7 外磁极径向厚度对电机效率的影响

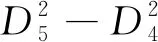
2 直线电机颤振力特性研究

对于空间制冷机而言，除了考虑效率、质量两个指标外，其自身引起的颤振也不能忽视[14]。制冷机的颤振会干扰空间探测器的测量精度和成象质量，从两侧电机的动力参数入手分析振动形成的具体原因，并与仿真分析相结合，提出控制压缩机颤振的参数调整方法，从源头减小制冷机的颤振量级。

2.1 一阶颤振特性分析

双活塞对置式压缩机在生产过程中不可避免存在材料属性偏差、零件尺寸偏差、质量偏差、充磁偏差等，使板簧刚度、动子质量、气隙磁场强度均有偏差，两侧动子的惯性力F=m·a不同，导致压缩机存在一阶颤振力，ΔF=Δ(m·a)=m·Δa+Δm·a+Δm·Δa。针对上述设计的电机进行了模拟仿真，量化分析了板簧刚度、动子质量和气隙磁场强度偏差对一阶颤振力的影响。由图8～图10可知：同行程下两侧板簧刚度、磁钢剩磁、动子质量偏差越大，一阶颤振力越大；差异相同时，电机驱动力F的提升带动活塞行程增大，一阶颤振力随着行程的增加而增加。

图8 两侧板簧刚度差异产生的一阶颤振力

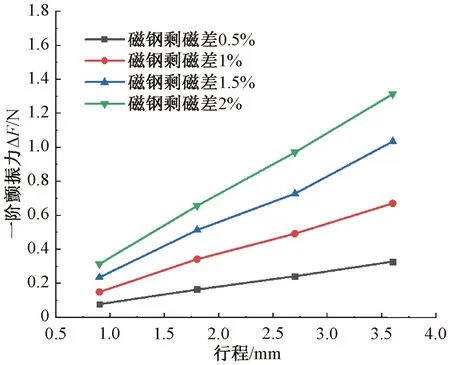
图9 两侧磁钢剩磁差异产生的一阶颤振力

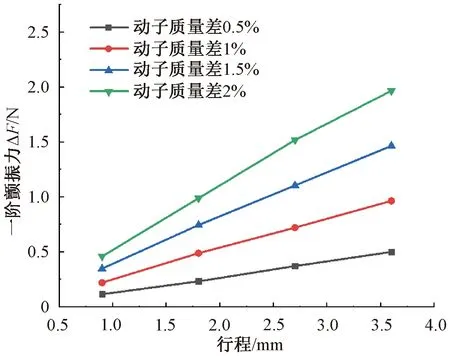
图10 两侧质量差异产生的一阶颤振力

实测压缩机A、B两侧动力参数如表2所示，动力参数差异使达到同活塞行程时两侧动子的一阶轴向力不同，此时压缩机就会产生一阶颤振力。

表2 电机两侧各参数状态

仿真发现，同行程下B侧产生的动能大于A侧，结合图8～图10，通过改变压缩机A侧动子质量,可使两侧动子的运动动能一致，将压缩机一阶颤振力降至较低水平。依据表2的参数状态，模拟分析了在A侧增加动子质量时的一阶颤振力输出情况，如图11所示。

图11 一阶颤振的仿真结果

2.2 二阶颤振特性分析

直线电机运行过程中，线圈产生的感应电动势形成的交变磁场存在二阶分量，使压缩机产生二阶颤振。在一些对振动敏感的场合，二阶颤振不能被忽视。本文对二阶颤振产生的原因及其具体数值进行定量化研究，为消除二阶颤振提供理论支持和数据支撑。Halbach阵列采用了双动圈电机，由于单个线圈穿越两个方向相反的磁场，故动子线圈在不同位置处电机的比推力BL变化剧烈，如图12所示。

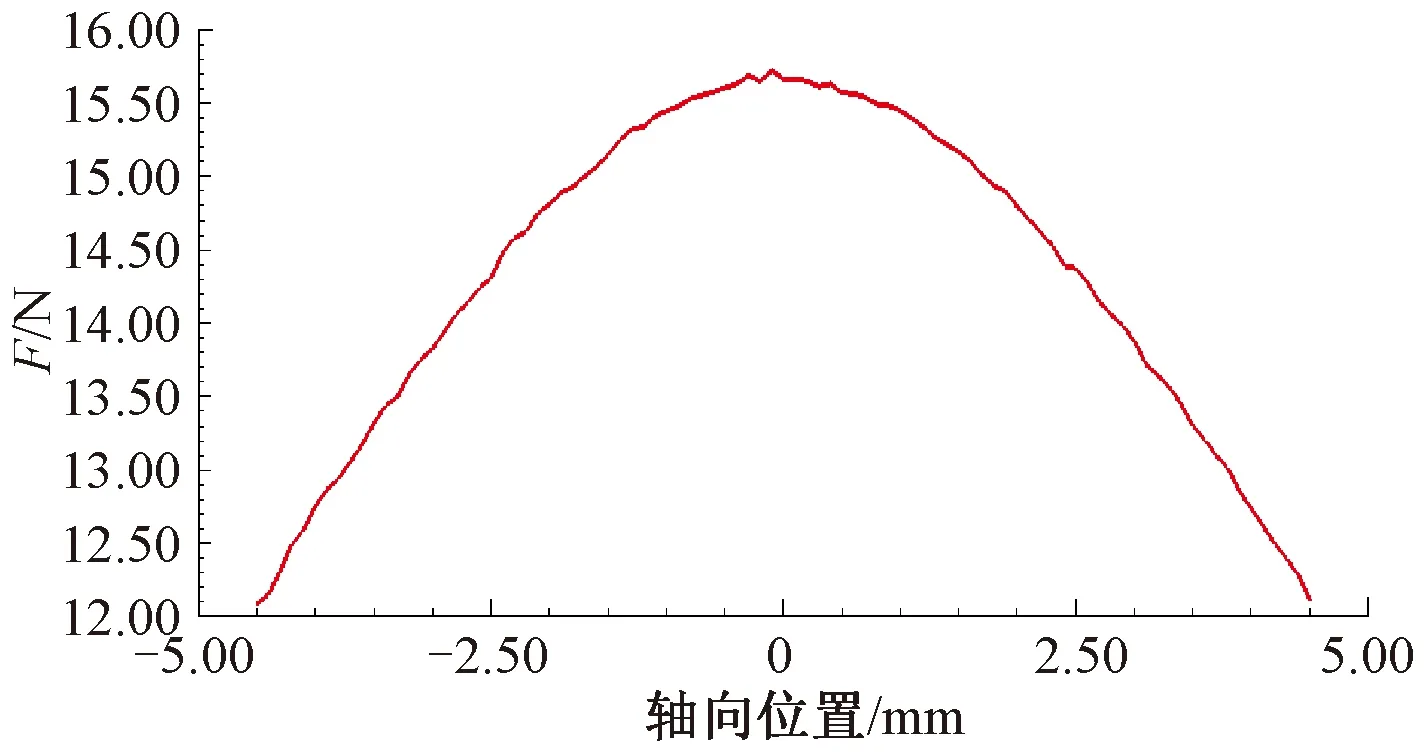
图12 双动圈比推力随轴向位置的变化曲线仿真

在实际装配中，压缩机两侧的位置偏差很小，即在两侧电机的差异落在图12上一小段较小的行程范围内，将该小段视为线性变化，此时比推力大小与位移的关系：

BL=kx+b

(15)

式中：k，b为与位移无关的系数；x为位移。电机总推力：

F=BLI=[kxmaxsin(ωt)+b]·

Imaxsin(ωt+φ)

(16)

式中：xmax为位移幅值；Imax为电流幅值；ω为角速度；φ为电流与位移的相位。将式(16)转化：

F=bImaxsin(ωt+φ)-kxmax·

Imax[cos(2ωt+φ)-cosφ]/2

(17)

由式(17)可知，推力出现了二阶分量，若两侧动子相对静子组件的轴向位移不一致，则同时刻两侧动子的位移不一致，产生的二阶颤振力也不相同，即衍生出压缩机的二阶振动。图13为电机一侧动子轴向平衡位置发生偏移，另一侧动子轴向平衡位置处于理论中心位置时的二阶颤振力仿真。根据二阶颤振仿真结果，随着偏置的增大、活塞位移的增加，二阶颤振力显著增加。

图13 电机动子不同轴向偏置和不同位移下的二阶颤振力仿真

3 实验研究

3.1 耦合冷指的压缩机电机性能测试

根据上述分析，研制了质量仅为4.5 kg的压缩机，其单侧电机质量为1.141 kg、外形尺寸为φ73.4 mm×43 mm，并将压缩机连接70 K冷指进行了相关实验验证。

图14 压缩机性能测试实验图

电机组件中内外磁极材料使用高磁导率的DT4E，其饱和磁感应强度达到2.4 T；线圈使用0.6 mm的漆包线，耐用电流为4.5 A；Halbach阵列磁钢材料均为N50H。制冷机达到6 W@70 K制冷量时压缩机的电参数如表3所示。

表3 6 W@70 K制冷量压缩机电参数

图15是压缩机连接冷指的性能测试实验结果，其中功耗为压缩机的输入电功，实测效率与有限元仿真下的电机效率非常接近。该方法可行性较强，具备一定的指导意义。

图15 制冷机制冷性能曲线图

3.2 电机颤振力特性测试

为了验证控制压缩机颤振力方法的有效性，搭建压缩机颤振测试平台，将压缩机与冷指耦合连接在颤振力测试平台上，通过测量轴线方向加速度值来计算压缩机的轴向颤振[15-16]。图16是动圈式压缩机改变A侧动子质量后的颤振力实测值和仿真值。可以看到，当A侧动子质量增加1 g时，一阶颤振明显减小，当A侧动子质量增加2 g时，相对于前者一阶颤振反而会增大，表明适当增加一侧动子质量对削弱一阶颤振有积极作用。调整A侧动子质量对压缩机轴向一阶颤振力的改善非常明显，±3.6 mm行程时，一阶颤振输出由原0.75 N消弱至0.25 N，衰减幅度达66.7%。

图16 实测压缩机轴向一阶颤振力

实验测试了压缩机样机的二阶颤振力，如图17所示。原状态二阶实测颤振力与图13中轴向偏移0.1 mm仿真值较为接近，这与实际装配过程中，每侧动子组件相对于静子组件轴向平衡位置的偏差在0.05 mm内，两侧动子轴向偏移绝对值在0.1 mm以内的实际工艺控制水平相符。基于上述电机平衡位置偏差对压缩机二阶颤振力的规律模拟分析，工艺上采用调整一侧电机的轴向平衡位置实现二阶颤振力的消减。由图17可以看出，A侧垫高0.05 mm后压缩机二阶颤振力有了大幅降低，二阶颤振力从2.3 N降低到0.5 N，衰减幅度达78.3 %，说明该方法起到了显著的减振效果。

图17 实测压缩机轴向二阶颤振力

4 结 语

本文建立了动圈式电机的等效磁路模型，分析了动圈式直线电机各部件尺寸参数对磁路和电机效率的影响，设计出一款质量小、推力大、电机效率高的动圈式线性压缩机。从电机本体入手分析了压缩机多阶颤振形成的具体原因，与有限元仿真分析相结合，量化压缩机两侧动子不同状态对一阶和二阶颤振力的影响，并提出控制压缩机颤振的方法。将线性压缩机与冷指进行耦合实验，性能测试结果验证了压缩机中电机设计方法的准确性，变参数颤振力测试结果验证了控制压缩机颤振方法的有效性。