应用SARIMA模型预测主题词研究热度

陈煜杰，王一蒙，任飞亮

(东北大学 计算机科学与工程学院，沈阳 110819)

E-mail:neu_chenyujie@qq.com

1 引 言

时间序列预测[1]是利用事物历史已有的数据进行统计分析，找到事物的发展规律，进而预测出事物未来的发展趋势.本文将采用文献发表数量来体现主题词的研究热度[2]，因此预测科技文献发表数量就成为了任务的关键所在.科技文献发表数量预测就属于时间序列预测任务，利用历史每年科技文献的发表数量，探究文献数量变化规律，进一步的预测出未来文献的发表数量.

科技文献是研究人员在科学研究的基础上，对研究现象或问题进行科学分析、合理创新、综合阐释而形成的电子和书面表达.科学技术的存在和发展是文献量变化的第一要素.当前时代技术更迭飞速，学科交叉催生众多新奇领域，科技文献的数目激增，从而出现了众多数字图书馆、文献数据库定期更新收录内容供用户查阅，但并未提供文献数量趋势预测功能.用户只能了解迄今为止已经形成的文献数量走向，而不能对其未来发展趋势做出科学预测.某一领域的科技文献发表数量与该领域的研究价值存在必然联系.通过有效预测科技文献数量趋势，能在一定程度上评判该领域具有的价值和已被开拓的价值，对于热门领域，为后继学者选择目标研究方向提供可靠依据，保证在有限时间内投入足够学术资源，实现更大程度的发掘和创新，同时科学预测还能有效调配市场资源，及时回收对于趋于饱和的领域的资源投入，转而形成部门联动，从资金、人力、政策等方面给更具潜力的领域的创新研究提供更有利的条件，实现资源的更高利用率，助力我国在新学科领域占据领军地位.

最早发现文献增长规律的是美国的Derek John de Solla Price[3]用“普赖斯曲线”模型指出科学领域内的文献数量是按指数增长的，且会在某一极限时达到饱和状态，这时文献数量转为线性增长.20世纪60年代前苏联科学家弗拉杜茨和纳米莫夫用“逻辑斯蒂曲线”[4]来修正和重新描绘文献的增长过程.英国情报学家Bertram Claude Brookes提出：随着科技水平的不断提高，已发表了的科技文献的价值将在某一时间范围内均匀地减少，并服从负指数规律.1958年，英国J.D.Bernal引入从放射性物质的“半衰期”引出文献的老化过程和老化速度.

但是科技文献按指数增长和按负指数老化规律都是在忽略一方的情况下，由统计经验得出，没有将其统一起来，在应用中人们容易产生对这两个规律与实际情况是否相符的疑问.因此当前方法的不足1：没有统一的评判标准，导致结果的信服程度低；不足2：只是简单的考虑到某一时间范围均匀地减少，没有对具体到季节变化进行模拟；不足3：最优解参数难以确定，迭代周期长.针对上述不足本文提出SARIMA模型，针对不足1采用AIC标准作为评判指标，AIC值越小拟合程度越好；针对不足2本文采用SARIMA模型将考虑季节性因素，使得结果更符合实际规律；针对不足3本文将对模型进行初步求参数，得到较小范围参数进而采用迭代法求出最优的参数.

利用本文构建的SARIMA模型，使用ACL Anthology收集的全部文献按年进行分类后得到每年发表的数量，将其作为要预测的历史数据，得到AIC值为515.617，相比于仅采用ARIMA模型提高了24.54%.

2 相关工作

预测科技文献的发表数量实际上是时间序列的预测问题，基于事物的发展是具有规律性和连续性的，使用过去已经发生产生的数据进行时间序列预测，推测出事物未来的发展规律.将常见的时间序列模型按照是否要求时间序列模型平稳可以分为平稳时间序列模型和非平稳时间序列模型，进一步地非平稳时间序列模型可以按照是否考虑季节性，分出季节性时间序列模型.本文讨论平稳时间序列模型，非平稳时间序列模型，季节性模型.

2.1 平稳时间序列模型

平稳时间序列模型要求输入的时间序列是平稳时间序列，平稳时间序列模型通常定义时会说明时间序列所要求的平稳条件.平稳条件定义为一个时间序列均值没有系统的变化，方差没有系统变化，且严格消除了周期性变化.如果不满足平稳条件则无法使用该模型.

其中最为经典的平稳时间序列模型有自回归模型(Auto-Regressive，AR)，移动平均模型(Moving Average，MA)，以及综合了两个模型的自回归滑动平均模型(Auto-Regressive Moving Average model，ARMA模型[5])，即ARMA(p，q)模型.该模型就是典型的对稳定性有较高要求，因此需要输入的时间序列为稳定性非白噪声序列，具有一定的局限性.

平稳时间序列模型对于生活中的大多数的规律难以模拟，因为无法保证时间序列的稳定性，应用性较低.

2.2 非平稳时间序列模型

非平稳时间序列模型不同于平稳时间序列模型，其不要求输入的时间序列为平稳时间序列.通常非平稳序列是包含趋势，拥有一种或多种的季节性或周期性.可以对不满足平稳条件的序列使用该模型.

其中最为经典的非平稳时间序列模型为差分整合移动平均自回归模型(Auto-Regressive Integrated Moving Average model，ARIMA模型[6])，该模型在ARMA(p，q)的基础上，加入了参数d，代表使得输入的时间序列变为平稳序列所做的差分次数，得到模型ARIMA(p，d，q)模型.该模型加入了参数d，使得模型可以用于非平稳的时间序列，推广性更好，应用范围也更广.

2.3 季节性时间序列模型

非平稳时间序列可以用来拟合季节性时间序列但是通常拟合效果较差.根据部分数据集有着如下特点，在某时间段内的一个固定区间内呈现相似的变化模式，那么就称该时间序列有季节性的特点.通常季节性时间序列模型对于有季节性的时间序列有较为不错的拟合效果.

其中经典的将非平稳时间序列与季节性联合的模型为Holt-Winters的加法模型[7].该模型是在Holt加入季节性变化方程构成的Holt模型该模型是指数平滑模型中的一种，可以成为趋势序列的通用模型.该模型较为简单，并且使用水平方程和趋势方程来拟合时间的变化，具有一定的可靠性，适用于随时间而连续变化的数据.进一步，根据时间序列的季节性特点加入季节分量方程，季节性方程考虑了t位置时刻的和上一区间的该位置时刻之间的联系，得到了Holt-Winters模型的预测方程.该模型在Holt模型增加了季节性因素因此对于周期固定的非平稳序列表现较好.

季节性时间序列在生活中普遍存在，例如商店的月营业额就收到淡季和旺季的影响，因此考虑时间序列的季节性可以进一步提升模型的预测能力.

3 方法描述

由于ARIMA模型没有考虑到季节性因素，因此对于拥有某时间段内的一个固定区间内呈现相似的变化模式的季节性数据，预测结果较差.因此本文提出，基于ARIMA的季节性模型，季节性差分整合移动平均自回归模型(Seasonal Autoregressive Integrated Moving Average，SARIMA[9，10]).该模型可以表示为SARIMA(p，d，q)(P，D，Q，m)其中p为自回归阶数，d为差分阶数，q代表移动平均阶数，P为季节性自回归阶数，D为季节性差分阶数，Q为季节性移动平均阶数，m为单个季节期间的固定时间的长度.

AR模型[8]的时间序列满足：

其中为常数项c，t满足E(t)=0，αi为自相关系数.该模型需要满足平稳条件为：

需要满足φ(x)= 0的根都大于1.

MA模型的时间序列满足：

MA模型的平稳条件为任何条件下都平稳.

将AR模型和MA模型组合相加得到：

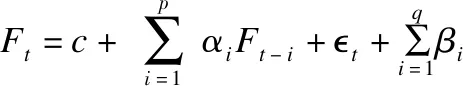
称该模型为(p，q)阶自回归滑动平均混合模型，即ARMA(p，q)模型.之后，加入了参数d，代表使得输入的非平稳时间序列变为平稳序列所做的差分次数，得到模型ARIMA(p，d，q)模型.进一步的，考虑季节性特征加入季节性自回归阶数，季节性差分阶数，季节性移动平均阶数，单个季节期间的固定时间的长度，模拟季节变化.

本文整体框架如图1所示，不难看出本文方法总体可以分为数据集构建，数据导入，数据平稳化，确定参数，模型结果5大部分，接下来详细介绍每步的细节.

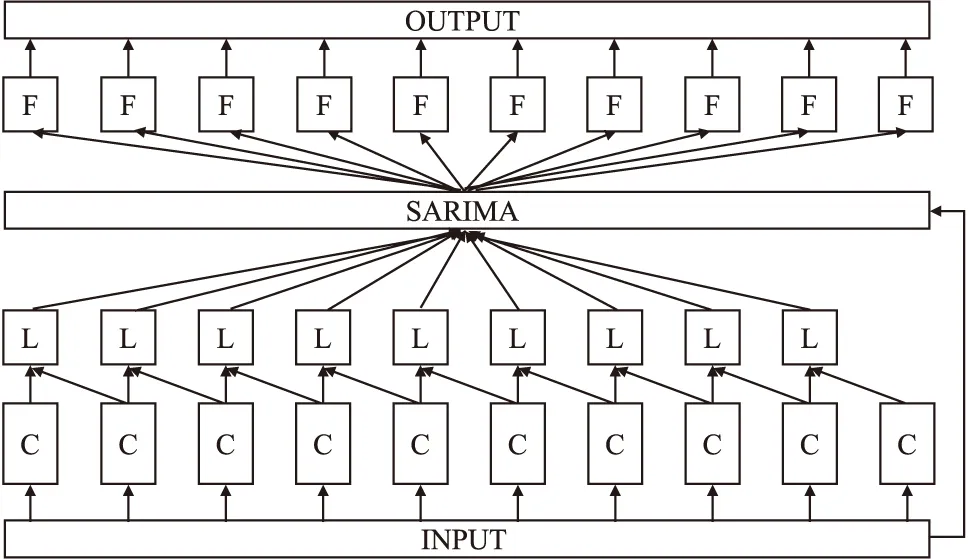
图1 模型结构图Fig.1 Model structure diagram

3.1 输入编码序列

在该模型中，将导入的数据编码为时间序列，自变量为连续变化的序列，因变量为每个时间对应的值.

由于数据的来源多样，因此未必所有数据都拥有规律.为了验证数据是否具有探索的必要性，即是否确实有规律值得探索，针对数据的特点，利用LB检验来检验原数据是否为白噪声序列.LB检验则是基于一系列滞后阶数，判断序列的相关性是否存在.

原假设H0：ρ1=…=ρh=0为设提供的数据之间都是相互独立的，能观察到的某些相关性仅产生于随机抽样的误差.

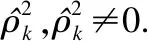
LB检验构造的统计量为：

3.2 序列转化

在本文提出的模型中，如果输入的时间序列为非平稳序列，就需要对原序列做差分处理.本文采用的是ADF检验(Augmented Dickey-Fuller test)来判断序列是否平稳.ADF检验是在Dickey-Fuller检验(DF检验)基础上发展而来的.ADF检验是一种随机的过程，用于判断原序列中是否有单位根.如果序列平稳，就不存在单位根.反之，则代表原时间序列为非平稳时间序列，则说明原序列不存在协整关系而出现伪回归现象，会使得结果失去意义.

ADF检验中如果Test Statistic是小于Critical Value(1%)、Critical Value(5%)、Critical Value(10%)，同时需要满足显著性水平低于0.05则可以拒绝原假设，认为数据是平稳的.

将数据进行时间序列化处理后，利用ACF检验，若非平稳则需要进行差分处理.若得到的时间序列依然是非平稳序列，则需要再进行差分处理直至时间序列为平稳序列.进行的差分次数即模型中参数d的大小，同时d的大小也等于D季节性差分阶数.

3.3 超参数确定

在数据平稳化中，已经确定了SARIMA模型中的d，D参数.还剩下p，q，P，Q，m未确定.其中m为单季节的固定时间的长度，需要根据滞后性与图像观测的共同参与得出，例如每年中图像都有相似的趋势，可以设m为12.

利用自相关系数ACF与偏自相关系数PACF来确定SARIAM模型中p和q的值.

定义Xt为给定的某一时间序列，xi为Xt时间序列中的一个点，则自相关系数ACF度量的是当前序列值xi和过去序列值xi-k之间的相关性.自相关系数ACF的公式可以表示为：

其中μt代表E(Xt)，E代表数学期望，D代表方差.

偏自相关系数PACF是用来描述随机过程中的结构特征，也是用来预测当前序列值xi和过去序列值xi-k之间的相关性，同时考虑k之间的值.在定义AR模型中，引入了αi自相关系数，则偏自相关系数PACF的公式可以表示为：

PACF=αk

求解的过程采用Yule-Walker方程进行求解.

根据利用自相关系数ACF与偏自相关系数PACF的函数图像可以初步确定p，q的值的范围，参数判断如表1所示.

表1 参数判断Table 1 Parameter judgment

通过函数图像观察值的范围难免有些主观，同时可以备选的模型较多，无法判断出哪个模型更优.因此接下来采用迭代法，在备选范围中选择出最优的参数.

3.4 模型预测

利用第4步所求的模型参数，进行模型建立求得建立的模型并进行预测，得到预测的时间序列.同时需要对最后的残差再进行白噪声检验，若结果证明了残差序列为白噪声检验，说明模型没有能再提取的信息.

4 实验及讨论

4.1 实验数据

ACLAnthology是一个关于计算语言学和自然语言处理的文献选集.本文的数据集为为ACL Anthology的文献元数据.ACL Anthology官网提供了自1965年～2020年以来共57029条文献的元数据.元数据的信息包括类型、唯一标识、标题、作者、书名、URL、时间、页码等.提供的文件为一个11.99MB的BibTex文件.

将BibTex文件进行转换按流的方式读入Python中，并且对日期字段进行格式化匹配将其转换为日期对象，形成时间序列.

本文将采用数据信息中的时间信息，由于论文的发表在一年中具有周期性，甚至部分月份没有论文发表同时数据集中存在部分数据仅提供了发表的年份，因此以年为维度统计每一年所发表的文献数量作为时间序列.通过在年份历史维度上得出论文的年发表量，说明科技文献的发表量趋势.相关数据统计信息如表2所示.

表2 统计信息Table 2 Statistical information

由于2019年、2020年数据不完整，因此本文选用1965年～2019年作为全部的测试集，其中1965年为2015年为训练集，2016年～2018为测试集.

4.2 评价指标

为了评价参数选取的好坏，本文提出采用AIC准则来确定剩余参数[11].AIC准则是衡量统计模型拟合效果优良性的一种准则，又称赤池信息量准则.它是建立在熵的概念基础上，可以判断出所采用模型的复杂度和此模型在拟合数据的表现，以此得出模型的优劣程度.

AIC公式：

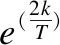
4.3 实验过程

4.3.1 输入编码序列

数据处理后画出时间序列图如图2所示，根据序列图所示在大约7年固定区间内有相似的变化模式，同时整体上呈现上升趋势采用SARIMA模型进行拟合.

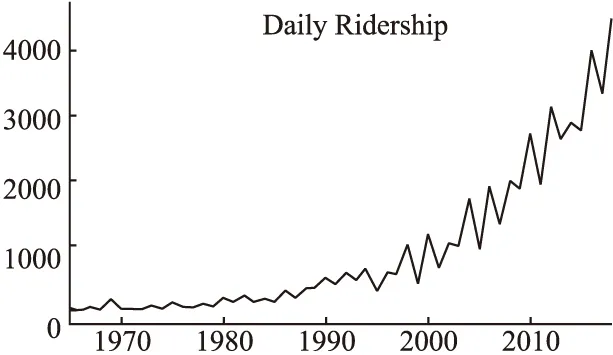
图2 论文年发表数量折线图Fig.2 Line graph of the number of papers published per year

采用白噪声检验，检验数据是否具有规律性.检验α结果值为1.35199e-10，可以拒绝原假设，可以认为原序列是非白噪声序列，说明原数据具有规律可以探索，符合模型建立的条件.

4.3.2 序列转化

采用ADF检验对序列的平稳性进行判断.第1次ADF检验结果如表3所示.

表3 第1次ADF检验结果Table 3 First ADF test results

从表中可以看出，Test Statistic结果为6.2018显然都大于Critical Value(1%)、Critical Value(5%)、Critical Value(10%).同时p-value所表示的显著性水平为1.0，大于理论好的0.05，显然原时间序列是不平稳的，符合使用SARIAM模型的特征.

因此为了消除原时间序列的不平稳性，接下来就需要对原数据进行差分处理，进行一次差分运算后发现数据仍然不满足平稳，因此再次差分，即对原数据进行二阶差分运算，得到结果如表4所示.

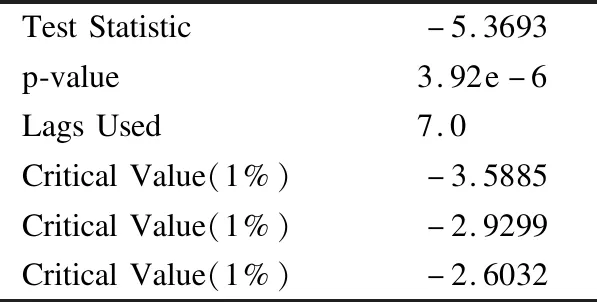
表4 第3次ADF检验结果Table 4 Results of the third ADF test

可以看出Test Statistic结果为-5.3693显然都小于3个Critical Value.同时p-value所表示的显著性水平为3.92e-6 <0.05甚至于小于0.01，因此可以认为数据经过二阶差分所得到的数据是平稳的.二阶差分得到的图像如图3所示.

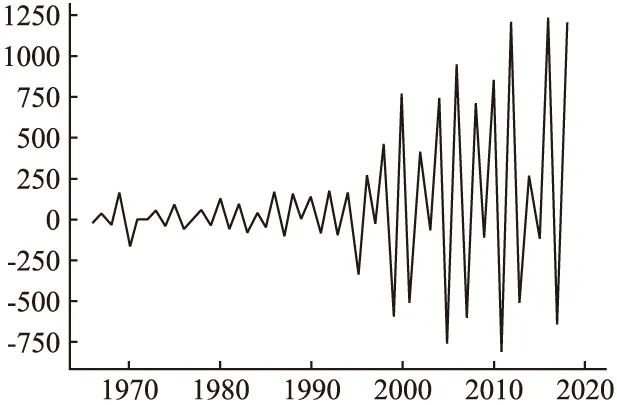
图3 二阶差分图像Fig.3 Second-order differential image

4.3.3 超参数确定

在训练集上，利用自相关系数ACF与偏自相关系数PACF来确定SARIAM模型中p和q的值.画出自相关系数ACF与偏自相关系数PACF图像如图4所示.

图4 自相关系数ACF与偏自相关系数PACF图像Fig.4 Autocorrelation coefficient ACF and partial autocorrelation coefficient PACF images

观察图像可以看出ACF图像ACF图拖尾，PACF为5时为0，则预选模型ARIMA(5，2，1)，ARIMA(5，2，0).同时ACF从4/6开始就基本落在2倍标准差范围，PACF是比较3/4开始预选模型因此可选模型因此p的取值可以是[4，6]，q的取值可以是[3，4].

确定SARIMA模型中的(P，D，Q，m)其中Q为差分阶数其值与d一致都为2.m为单季节的固定时间的长度，根据滞后性与图像观测，本文将m设为7.

接下来剩下(P，Q)还未确认，同时ARIMA模型中的(p，q)还未确定某一个具体模型，因此设参数组(p，q，P，Q)采用AIC准则使用SARIMA模型，根据AIC准则可知，AIC小的参数代表拟合效果好，因此选出了参数组(4，3，1，0)作为模型最终的参数.

至此SARIMA模型建立完成为SARIMA(4，2，3)(1，2，0，7)模型.

4.3.4 模型预测

利用训练集上1965年为2015年历史数据得到的参数，使用SARIMA(4，2，3)(1，2，0，7)模型，在测试集上得到预测结果如图5所示.

图5 预测结果Fig.5 Prediction results

通过图像可以看出预测基本拟合了测试集的趋势，甚至值都相差无几.模型最后所得的AIC值为505.859.最后再次对模型的残差进行白噪声检验，所得到的p-value=0.415>0.05，说明模型已经没有能够再探索规律的余地，至此实验结束.

4.4 实验讨论

本文在实验上，最后结果采用AIC标准作为评判指标，使得对结果有了一个客观的评价，具有科学性；针对不足2，本文采用SARIMA模型将考虑季节性因素，使得结果更符合实际规律，利用本文数据采用SARIMA模型与ARIMA模型可以得到对比结果如表5所示.

表5 模型结果对比Table 5 Comparison of model results

可以看到模型最后所得的AIC值为505.859，如果仅采用ARIMA(4，2，3)模型得到的AIC值为646.363，说明采用SARIMA模型对于原数据的拟合效果更好；同时实验采用图像+迭代法求最优解参数：对模型进行初步求参数，得到较小范围参数进而采用迭代法求出最优的参数，以此来减少模型迭代所花时间.

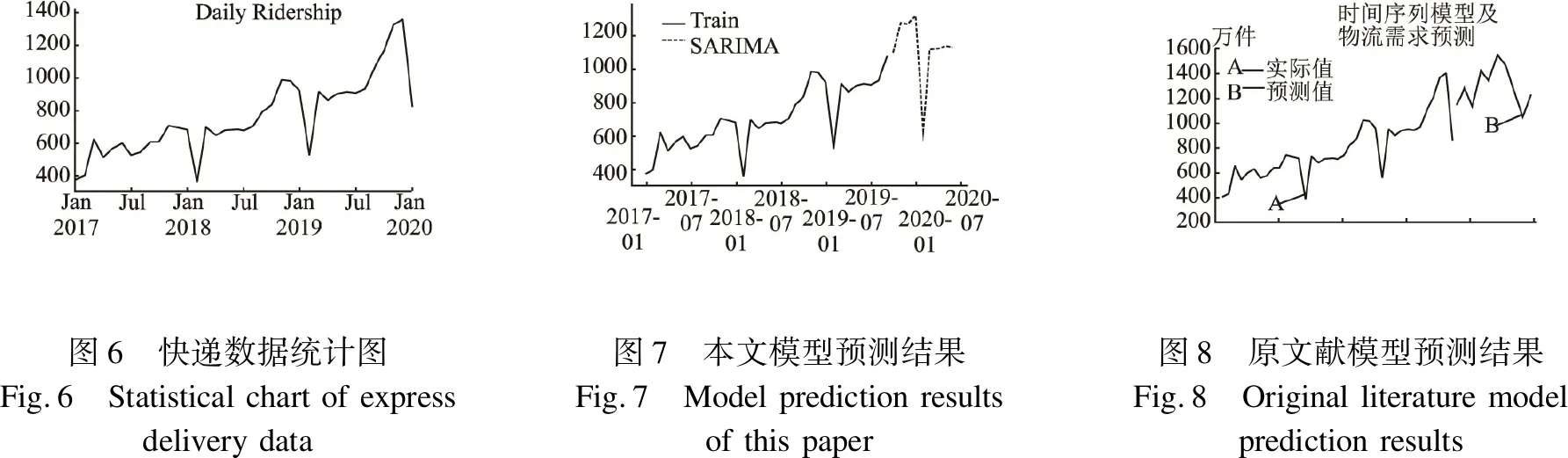
SARIMA相比于ARIMA的优势在于多了一个季节性因素.由于事物的发展往往是有规律的，因此许多现象都有着季节性预测，文献[12]对长春物流的预测，观察数据的图像如图6所示，显然可以看出该数据集具有季节性，尤其是1、2月份有一个很明显的下滑趋势，同时可以很容易看出该数据单季节的时间长度为12.

采用原文献中的ARMIA模型，p=1，d=2，q=1即构造出了ARIMA(1，2，1)模型，所得到的最后结果AIC为400.069，而如果采用本文中所提出的SARIMA模型，通过本文提出的建模过程建立模型，最后确定模型为SARIMA(1，1，1)(2，1，0，12)得到的AIC为241.387.结果相比于使用ARIMA(1，2，1)模型更优.同时通过观察图7与图8，显然本文的所用的SARIMA拟合效果更好，在预测整体趋势上有较强的能力.

5 结 语

本文利用55年以来科技文献发表数量的时间序列预测未来科技文献的发表情况.采用了AIC指标作为评判模型好坏的指标，使得对结果有了一个客观的评价，具有科学性；本文采用SARIMA模型，考虑季节性因素，使得结果更符合实际规律，实验结果表明使用SARIMA相比于ARIMA模型有更好的预测能力；采用图像+迭代的方式，减少迭代求解的时间的同时保证解的准确.进一步的，模型建立过程应用与其他领域，例如物流预测，发现预测效果相比于相比于ARIMA模型也表现优秀.因此可以得出结论，具有季节性的数据，采用本文建立SARIMA模型办法，有助于提高模型的预测准确率.

本文提出的SARIMA模型在预测具有季节性的非稳定时间序列表现良好.在本文的数据集上，最后的残差检验结果为白噪声.但是若差检验结果为非白噪声序列，那么需要继续提取序列中的有效信息，以提高预测准确率.本文提出一种可行的解决方案，利用SARIMA模型与广义自回归条件异方差模型[13](Generalized Autoregressive Conditional Heteroskedasticity Model，GARCH[14])进行结合来进一步增加预测的准确率.在使用SARIMA模型进行预测时，容易忽略时间序列的异方差和波动聚集特性.因此采用GARCH模型收集时间序列中的异方差属性，对模型结果进行调整以提高模型准确率.

本文采用的数据集是来自ACL Anthology该数据集文章的研究领域是计算语言学和自然语言处理，通过本文预测看出计算语言学和自然语言处理领域的论文发表量越来越多，预测结果表面未来该领域仍有一定热度.利用本文提出的模型，采用不同的主题词文献数据集，进一步预测相关主题词的文献未来发表数量情况.通过有效预测文献数量发表趋势，能在一定程度上评判该领域具有的价值和已被开拓的价值：对于趋势为下降的关键词可以认为该领域渐渐趋于冷门，说明已被开拓了该领域大部分价值；而对于趋势为上升的关键词可以认为是热门领域，尚且有开拓价值.对于刚踏入科研的后继学者提供了选择目标研究方向的可靠依据，保证在有限时间内投入足够学术资源，实现更大程度的发掘和创新，有助于我国在新学科领域占据领军地位.