渗透水/气压反复循环下软岩剪切蠕变试验及本构模型研究
2022-10-14黄良慧
胡 斌,黄良慧,丁 静,李 京,崔 凯,刘 霁
(1.武汉科技大学 资源与环境工程学院,武汉 430081;2.武汉科技大学 冶金矿产资源高效利用与造块湖北省重点实验室,武汉 430081)
在我国西南地区,随着露天矿山开采规模的不断扩大与开采深度的增加,在矿山边坡中揭露了大量的二叠系软弱夹层。该类软弱夹层遇水易软化、力学特性差,往往是造成边坡失稳的“罪魁祸首”,尤其是在雨水的反复浸泡-疏干作用下,其流变特性极为显著,这将对矿山高陡边坡的长期稳定性造成不利影响[1]。
国内外学者已经开展了大量软弱夹层蠕变特性研究,并取得了丰富的研究成果。王松鹤等[2]开展了黄土剪切蠕变试验研究,提出了一种新型的对数型经验模型;朱赛楠等[3]通过室内炭质页岩剪切蠕变试验,发现滑带、层间剪切带与原岩试样的蠕变位移与蠕变速率逐渐减小;韩世亮等[4]开展了坝基软岩的饱水劣化蠕变试验,建立了一个考虑损伤变量的本构模型;李鹏等[5]通过软弱结构面剪切蠕变试验,发现随着试样含水率的增高,长期强度在降低;LIU等[6]对深部角闪岩进行了干燥和饱水条件下的蠕变加卸载试验,发现高应力下水对岩石的蠕变特性影响较大;徐辉等[7]对武汉越江隧道围岩中的饱水砂岩进行了剪切流变试验研究,基于得到的剪切流变试验曲线,提出一种I-NVPB模型,对全过程剪切流变曲线进行了模拟,同时获得了饱水砂岩的全部剪切流变参数;徐卫亚等[8-11]对饱和状态下的大理岩和绿片岩进行了三轴蠕变试验,分析了饱和状态下的蠕变破裂机理;黄小兰等[12]对不同含水率的泥岩进行了蠕变试验,建立了考虑含水率的蠕变本构方程;朱合华等[13]进行了干燥与饱水两种状态下岩石蠕变试验,探讨了岩石蠕变受含水率状态影响的规律;张泽林等[14]通过室内试验剪切试验和数值模拟,发现软弱夹层的破坏是从内部开始;程强等[15]开展了红层软岩剪切蠕变试验,发现红层软岩长期强度为直剪强度的75%;于永江等[16]基于软岩室内试验结果,建立了可以描述软岩非线性破坏的本构模型,并利用BFSS算法对该模型进行了参数识别;范秋雁等[17]开展了膨胀岩剪切蠕变试验,探究了膨胀和蠕变耦合方式对长期强度的影响;唐佳等[18]通过室内蠕变试验,在基于摩尔库伦准则的基础上提出了M-C塑性元件,可用于模拟粘弹塑性偏量特征。
已有的研究主要集中于常规蠕变条件下,对于雨水反复作用下软弱夹层剪切蠕变的研究鲜有报道。虽 然 FUJII[19]、王 新 刚[20]、赖 远 超[21]、周 海波[22]和李安润等[23]开展了大量软弱夹层在饱水-干燥反复循环作用下的剪切蠕变试验研究,但这些研究中软弱夹层的干湿循环均在试验前完成,在试验过程中试样含水率并未发生改变,这与实际情况中软弱夹层在上覆荷载作用下持续产生变形的同时,仍不断经历雨水浸润-疏干-浸润-疏干…长期反复劣化作用的过程存在差异。
基于此,本文采用在试验过程中通过水/气压力转换改变软弱夹层含水率,模拟雨水的反复作用,开展了软弱夹层在渗透水/气压循环作用下的剪切蠕变试验,分析了软弱夹层的蠕变变形特性与水/气压循环对长期强度的影响,并在此基础上建立了蠕变损伤本构模型,结合试验数据,对模型的合理性与正确性进行了验证。研究结果对含软弱夹层矿山高陡边坡的长期稳定性研究具有重要指导意义。
1 试验材料及过程
1.1 试样制作及设备
本次试验材料取自四川金顶集团黄山石灰石矿区中部老鹰嘴边坡(图1),岩性为炭质页岩。将所取的试验材料加工为试验所需标准长方体(150 mm×75 mm×75 mm)试样,并对试样六个端面进行打磨,保证试样端面的平行度在0.02 mm以内,以降低试验误差;使用钻机在试样表面平行于剪切方向的中心线上钻出三个等孔距的渗流孔,孔距为37.5 mm,为保证水/气压能够快速作用在预定剪切面上,渗流孔深度为37.5 mm,孔径为8 mm,如图2所示。

图1 取样地点图Fig.1 Sampling site diagram
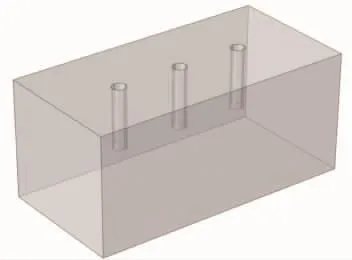
图2 试样结构Fig.2 Specimen structure
1.2 试验装置
试验是在自主研制的软岩剪切流变试验装置上完成的,该装置主要由渗流系统、压剪系统和数据监测与采集系统三部分组成,如图3所示。该装置法向/切向方向上均设有伺服电动缸,用于施加法向/切向试验力,在伺服电动缸内设有压力传感器与位移传感器,用于测量法向/切向方向的试验力和位移。

图3 软岩剪切流变试验装置Fig.3 Soft rock shear rheological test apparatus
为保证上剪切盒与下剪切盒接触面具有良好的密封性,上、下剪切盒通过四根竖向辊轴和两块移动滑板连接,在上剪切盒设有供辊轴沿剪切方向运动的通孔,能保证上、下剪切盒在竖向上的连接,同时又能保证上、下剪切盒可沿剪切方向错位,且在上、下剪切盒接触面设有矩形密封圈进行密封;渗透水压由渗流加压装置经法向加载压头内部入水通道接入试样渗流内,如图4所示。在试验过程中,法向荷载由法向伺服电动缸施加在剪切盒法向加载压头上,再通过法向加载压头传递到试样表面,剪切荷载则通过左侧伺服电动缸直接施加在下剪切盒左端面,上剪切盒因受到右侧反力杆的作用而保持静止,如图5所示。

图4 剪切盒示意图Fig.4 Schematic of the clipping box

图5 加载实物图Fig.5 Loading the physical image
1.3 试验设计
雨水反复作用导致的是软弱夹层含水率的变化[24],因此,在试验过程中采用水/气交替注入的方式来改变软弱夹层含水率,以达到浸润-疏干-浸润反复循环的目的,该试验方法相较于传统试验前干湿循环更加贴合实际工程需求。存在于矿山高陡边坡中的软弱夹层在经受雨水浸润过程中,还会受到因雨水沿边坡岩体节理、裂隙入渗形成的渗透水压作用,为真实还原软弱夹层在浸润时所处水文地质条件,在试样浸润过程中施加1 MPa渗透水/气压力。以施加1 MPa渗透水压,4 h后再施加1 MPa渗透气压,4 h为一次循环,渗透水/气压力的循环在施加第四级剪切应力前结束。试样需分别进行n=0、3、6、9次的循环,因此,在前三级剪切应力施加后,需在每一级剪应力稳定后分别完成n=0、1、2、3次的渗透水/气压力循环。
本次试验共分为4组,各组试验方案如表1所示。剪切蠕变试验采用分级加载方式,以自然状态下软弱夹层的抗剪强度作为剪切蠕变试验分级加载的依据,分4~7级施加剪切应力。试验步骤为:1)安装试样,施加法向应力,当法向应力与法向变形均稳定后,施加第一级剪切应力。2)第一级剪切变形稳定后,开始施加第一次渗透水/气压循环。3)在渗透水/气压力循环结束后,观察试样的剪切蠕变变形,当蠕变变形小于0.003 mm/h后,可以施加下一级剪切应力。

表1 试验方案Table 1 Test protocol /MPa
2 试验结果分析
2.1 软弱夹层剪切蠕变特征
对本次试验数据采用Boltzmann处理,经处理后的不同渗透水/气循环次数下软弱夹层试样蠕变曲线如图6所示,其蠕变变形特征具体可以概括为以下几点:
软弱夹层试样在各级剪切应力均产生瞬时弹性变形,但产生的瞬时变形量不相同,在第一级剪切应力作用下,因软弱夹层试样内部存在孔隙与裂隙,产生的瞬时剪切变形较大。
各组软弱夹层的剪切蠕变试验表现出了明显的蠕变三阶段特征,在较低剪切应力作用下,软弱夹层试样在较短时间内进入了减速蠕变阶段,剪切变形量几乎不再变化,剪切蠕变速率为很小的值或近似为0;随着剪切应力的增加,试样蠕变变形增大,蠕变曲线变陡,蠕变速率增大,最终趋于一定值,试样进入稳定蠕变阶段;当剪切应力施加至最后一级时,试样进入加速蠕变阶段,蠕变变形急剧增加,直到试样发生破坏。
在施加最后一级剪切应力后,软弱夹层试样出现了两种不同的破坏形式。当最后一级剪切应力施加完后,试样直接进入加速蠕变破坏阶段,如图6(a)和图6(d)所示,属于脆性破坏;而在图6(b)和图6(c)中,在最后一级剪应力作用下,试样在经历了减速蠕变和稳定蠕变阶段后才进入加速蠕变破阶段,属于韧性破坏。造成试样呈现两种破坏形式主要是因为在图6(b)和图6(c)中施加的最后一级剪切应力刚好等于试样出现蠕变三阶段所需的剪切应力,而图6(a)和图6(d)中最后一级施加的剪切应力则大于该值。

图6 不同渗透水/气循环次数下软弱夹层试样蠕变曲线Fig.6 Creep curve of a weak sandwich specimen under different permeation water/gas cycle cycles
试验过程中渗透水/气压循环次数为0、3、6、9的试样 在破坏前分别产 生 了 0.94、1.14、1.26、1.27 mm蠕变变形量,呈递增趋势。表明随着试验过程中水气/压循环次数的增加,软弱夹层在破坏前的剪切变形量在增大。
2.2 软弱夹层长期强度特征
2.2.1 软弱夹层长期强度的劣化
岩体长期强度是指岩体在长期荷载作用下(t→∞)岩体抵御破坏的强度值,当岩体所受荷载大于此值时,岩体由稳定蠕变向加速蠕变转变,在很短时间将发生破坏;小于此值时,岩体蠕变则按减速蠕变或稳定蠕变发展。岩体的长期强度是评价工程岩体稳定性的重要指标,对边坡稳定性的研究至关重要。因此,本文采用《水利水电工程岩石试验规程》(SL264-2020)中所提出的剪切应力-剪切变形等时簇曲线来确定软弱夹层长期强度。
不同循环次数软弱夹层剪应力-剪切变形等时簇曲线如图7所示。由图7可知,经历水/气压循环0、3、6、9次后软弱夹层试样的的长期强度分别为3.91、3.20、2.40、2.13 MPa,长期强度呈递减趋势。

图7 不同循环次数软弱夹层剪应力-剪切变形等时簇曲线Fig.7 Shear stress-shear deformation isochronous cluster curve of weak interlayer with different cycle times
为更好地反映渗透水/气压循环次数对软弱夹层长期强度的影响规律,引入长期强度劣化度(Dn),表征长期渗透水/气压循环对软弱夹层长期强度的劣化程度。

式中,τ∞(0)为软弱夹层水/气压力循环0次后的长期强度,τ∞(n)为软弱夹层水/气压力循环n次后的长期强度。
表2给出了软弱夹层长期强度劣化度随水/气压循坏次数变化的结果,从表2中可知,软弱夹层长期强度劣化度随着试验过程中渗透水/气压循环次数的增加而增大,在循坏3次后长期强度下降18.16%,循环6次后长期强度下降38.62%,循环9次后长期强度下降45.52%。

表2 长期强度劣化度随水/气压循坏次数变化Table 2 Long-term strength deterioration varies with the number of water/barometric pressure cycles
图8给了劣化度与循环次数的拟合曲线,拟合结果为:
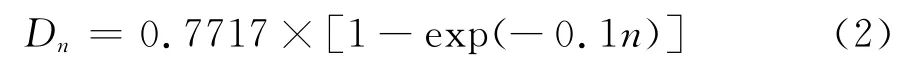
从图8可知,随着水/气压循环次数的增加软弱夹层长期强度劣化度在逐渐增大,但不会无限劣化,而是最终趋于一个稳定值,这表明经历无数次渗透水/气压循环后的软弱夹层不会直接发生破坏,而是仍具有一定的强度。
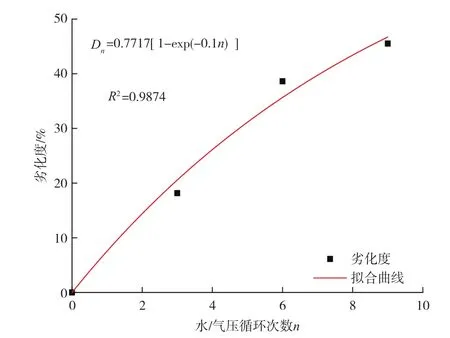
图8 劣化度与水/气压循环次数n的拟合曲线Fig.8 Fitting curve of the degree of deterioration to the number of water/barometric cycles n
2.2.2 长期强度劣化机理分析
根据本文开展的剪切蠕变试验,结合张娜等[25-27]关于水与软岩相互作用的研究,对软弱夹层长期强度劣化机理分析如下:1)水沿着软弱夹层原生孔隙进入软弱夹层内部,其中可溶性物质将被溶解,内部微观结构被改变,颗粒之间胶结力降低;2)通过开展矿物成分分析发现,该软弱夹层主要由伊利石、石膏、石英、方解石和黄铁矿组成,其中伊利石具有亲水性,在吸水后其晶层间膨胀力将扩大一倍,极易导致软弱夹层发生崩解和软化;3)软弱夹层在剪应力作用下其内部产生裂纹,裂纹导水/气,形成水/气渗流路径,渗透水/气压力在已形成裂纹中为裂纹扩展提供张力,加剧裂纹发展速率;因此,随着试验过程中渗透水/气压循环次数的增多,软弱夹层长期强度的劣化越严重。
3 本构模型
3.1 剪切蠕变本构模型辨识
蠕变本构模型是将室内试验与工程实际联系起来的关键,因此,在实际应用中,需根据岩石的蠕变特性来建立合适的蠕变模型。从图9可知:1)在每一级施加剪切应力时,软弱夹层试样均产生瞬时弹性变形,说明该模型中应存在弹性元件;2)在较高应力水平作用下,软弱夹层的剪切变形随时间变化呈正相关,说明该模型中存在黏性元件;3)在剪切应力超过某一值时,软弱夹层将进入第三蠕变阶段,直到发生破坏,说明该模型中还应存在塑性元件。由于传统的广义凯尔文体、伯格斯体等本构模型无法描述软弱夹层的加速流变阶段,因此本文在传统本构模型基础上,建立一个可以描述软弱夹层黏弹塑性的渗透水/气压循环蠕变损伤模型。

图9 渗透水/气压循环蠕变损伤模型Fig.9 Permeable water/barometric cyclic creep damage model
3.2 本构模型建立
渗透水/气压循环蠕变损伤模型如图10所示,该模型有 A、B、C三个组件构成。其中,k1、k2(n)为弹性模量,η1、η2(n)、η3为黏性系数、τS为屈服强度,ε1为 A组件的应变,ε2为B组件的应变,ε3为C组件的应变。
模型中A组件为凯尔文体,其蠕变方程为:

式中,τ为长期强度,k1为弹性模量,η1为黏性系数。
模型中B组件为考虑渗透水/气压循环次数的黏弹性体。软弱夹层经历多次渗透水气压循环后,力学特性被劣化,其力学参数是随着循环次数n变化的非常定参数。因此,引入组件B,承担软弱夹层经受水/气压力循影响产生的蠕变增量。当剪切应力相同时,无需讨论n对组件A与组件C中的参数的影响,可减少模型中非常定参数的量,将模型简单化。k2、η2与循环次数n有关,即:

其蠕变方程为:
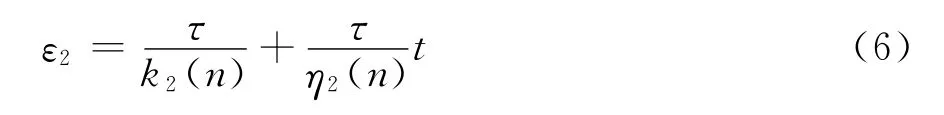
式中,τ为长期强度,k2(n)为弹性模量,η2(n)为黏性系数。
模型中C组件为考虑统计损伤变量的黏塑性体。由于传统本构模型无法描述软弱夹层的加速蠕变阶段,存在局限性。因此引入了统计学与概率论中的Weibull分布理论,本文认为当剪切应力达到或超过屈服应力时,软弱夹层的损伤符合 Weibull分布,其损伤变量的概率密度函数可以表示为一个与流变时间t有关的函数:
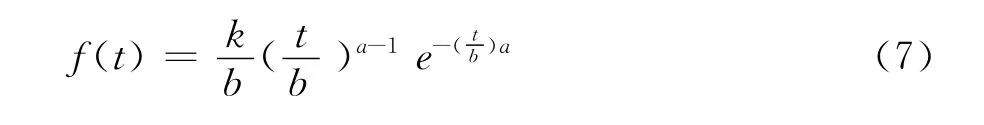
式中,a为形状参数;b为比列参数,为简便计算,取b=1。
t时间后损伤变量D i可表示为:
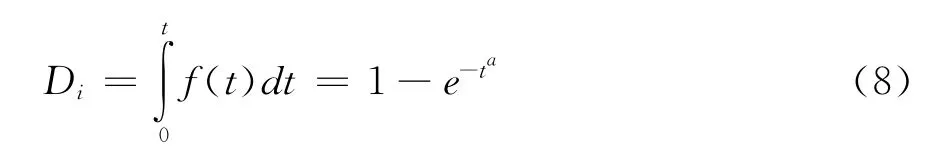
则可得C组件蠕变方程为:

式中,τS为屈服强度,η3为黏性系数。
根据元件组合模型的串联性质。可得渗透水/气压循环蠕变损伤模型的蠕变方程为:

3.3 剪切蠕变本构模型验证
利用本文已建立剪切蠕变本构模型,使用Origin数值分析软件采用“试错法”对图6中的剪切蠕变试验数据进行拟合,求解模型中参数。限于文章篇幅,本文仅列出试样循环次数为0的蠕变参数辨识结果(表3)。

表3 n=0时蠕变模型中各参数值Table 3 The values of each parameter in the creep model at n=0
表4给出了软弱夹层循环结束后模型中k2(n)与η2(n)参数的平均值,通过曲线拟合,如图10所示,发现k2(n)与η2(n)与循环次数n呈指数关系:

表4 k 2(n)与η2(n)参数平均值Table 4 the average of the parameters k 2(n)andη2(n)

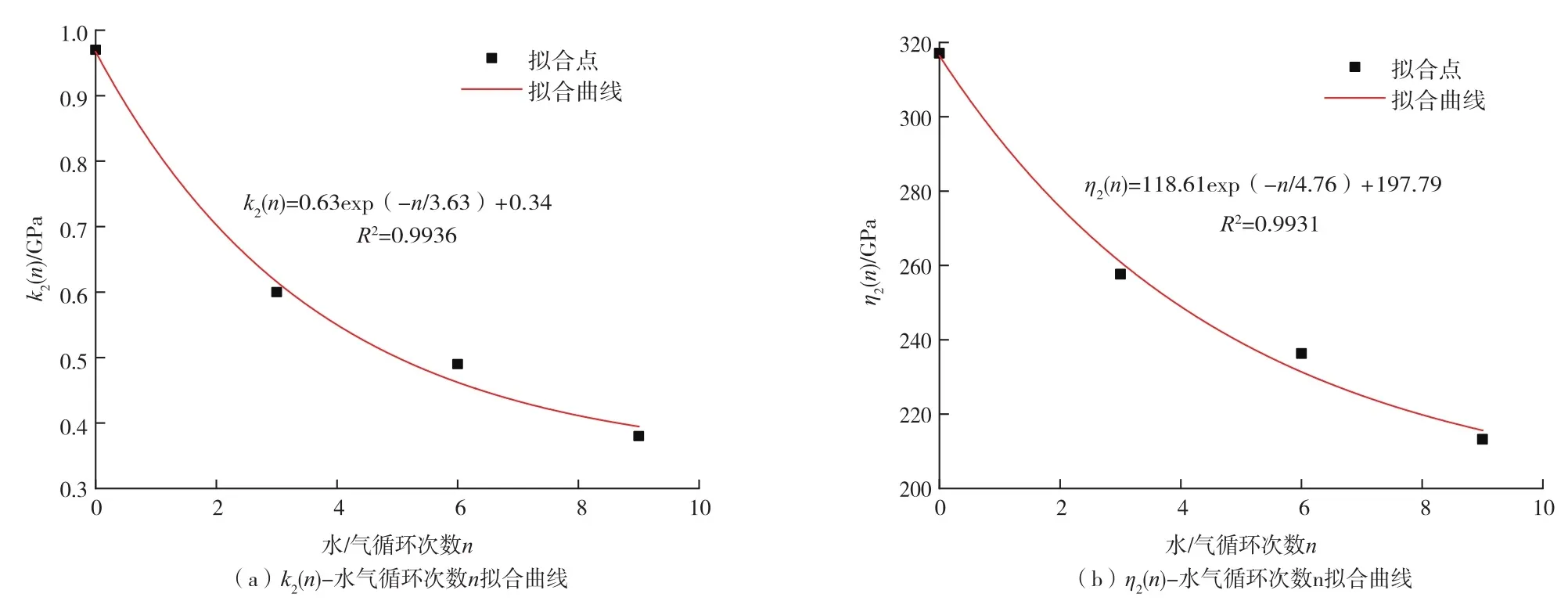
图10 参数k 2(n)、η2(n)-水气循环次数n拟合曲线Fig.10 Parameters k 2(n),η2(n)-water vapor cycle number n fitting curve
图11为试验曲线与模型曲线地对比图,从图11可以看出,试验结果与模型曲线拟合的很好,相关性系数较高,R2均在0.95以上。表明建立的蠕变损伤模型是合理的、正确,可以很好反应软弱夹层在渗透水/气压循环作用下减速蠕变、稳定蠕变、加速蠕变的时效力学行为。

图11 数值拟合曲线与试验曲线Fig.11 Numerical fitting curve and test curve
4 结论
本文通过开展渗透水气压循环作用下软弱夹层剪切蠕变试验,得出了以下结论:
1)软弱夹层剪切蠕变试验出现了明显的蠕变三阶段特征,在施加最后一级剪切应力时,软弱夹层很快进入了加速蠕变阶段,在破坏时呈现出韧性与脆性两种不同的破坏形式。
2)随渗透水/气压循环次数的增加,软弱夹层的劣化程度逐渐增大,最终趋于一定值,其劣化程度可用函数Di=0.7717×[1-exp(-0.1n)]来表示。
3)基于剪切蠕变试验结果,引入 Weibull分布理论,建立了一个可以描述软弱夹层剪切蠕变特性的损伤模型,经拟合分析,该模型与试验结果拟合度高,说明了所建立模型是正确的、合理的,研究成果可为含软弱夹层的矿山高陡边坡稳定性分析提供理论支持。
